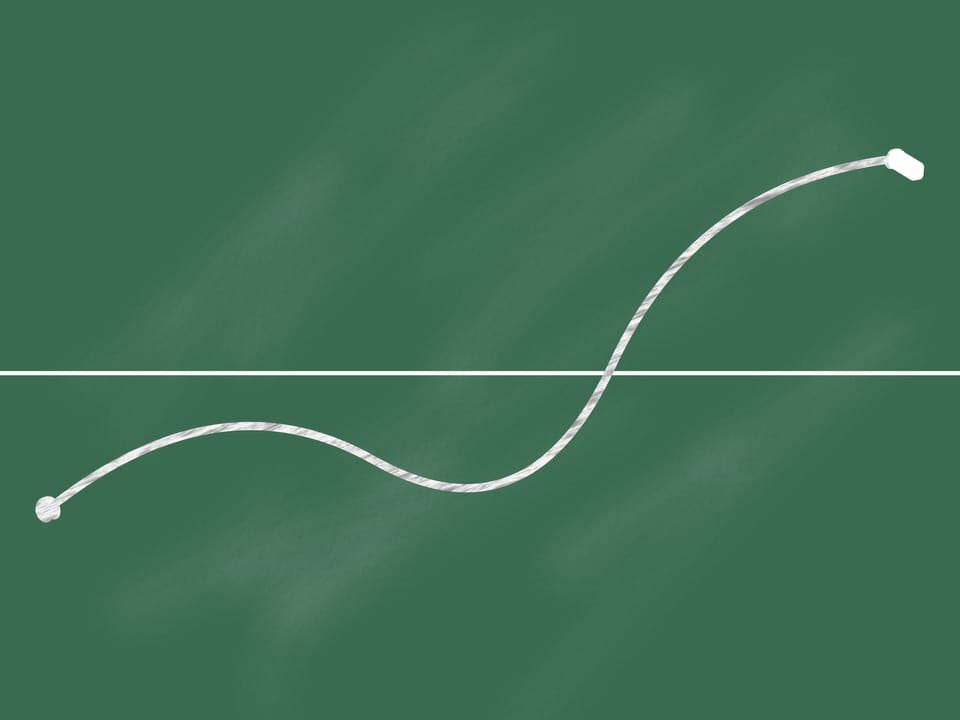
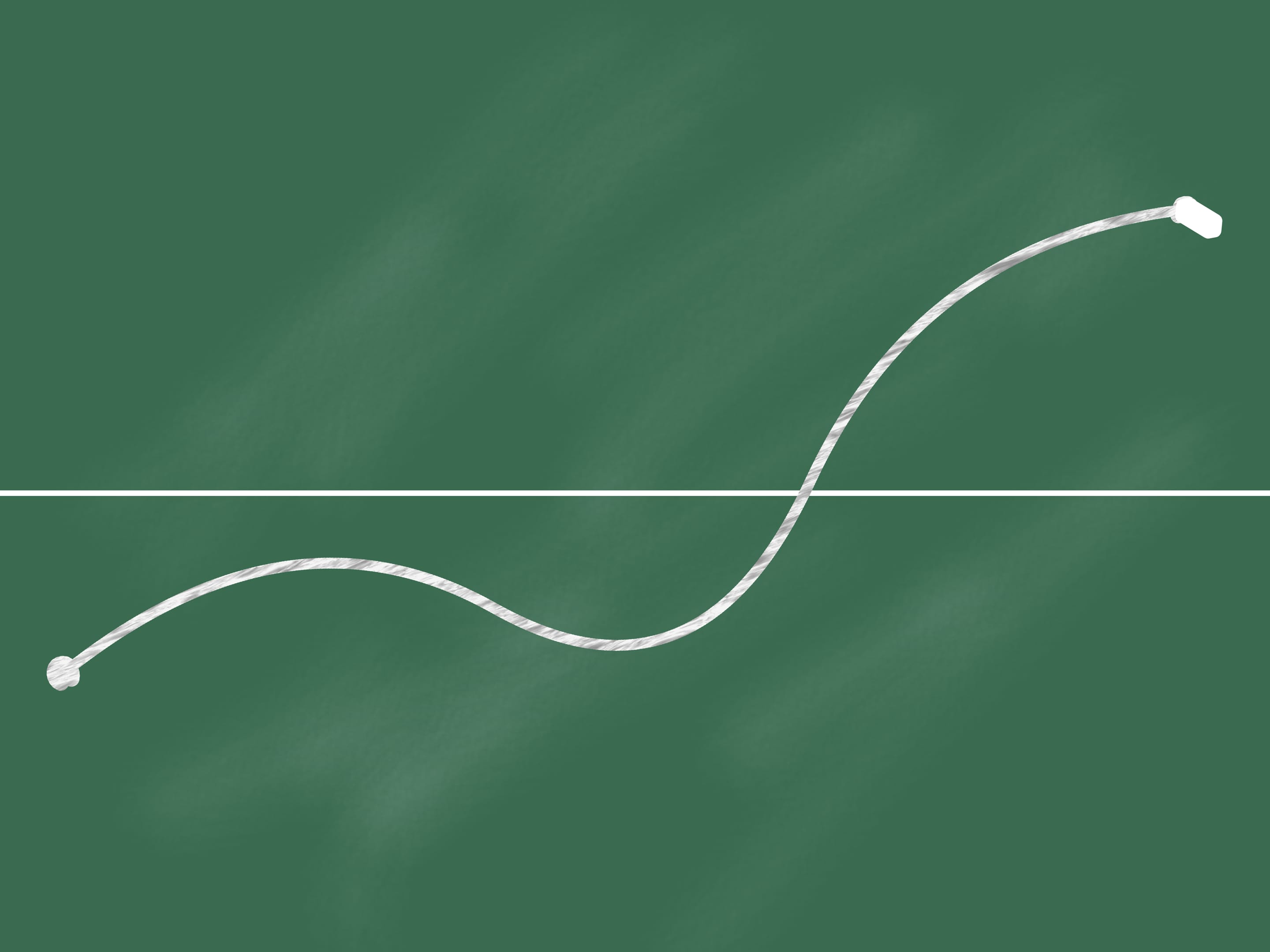
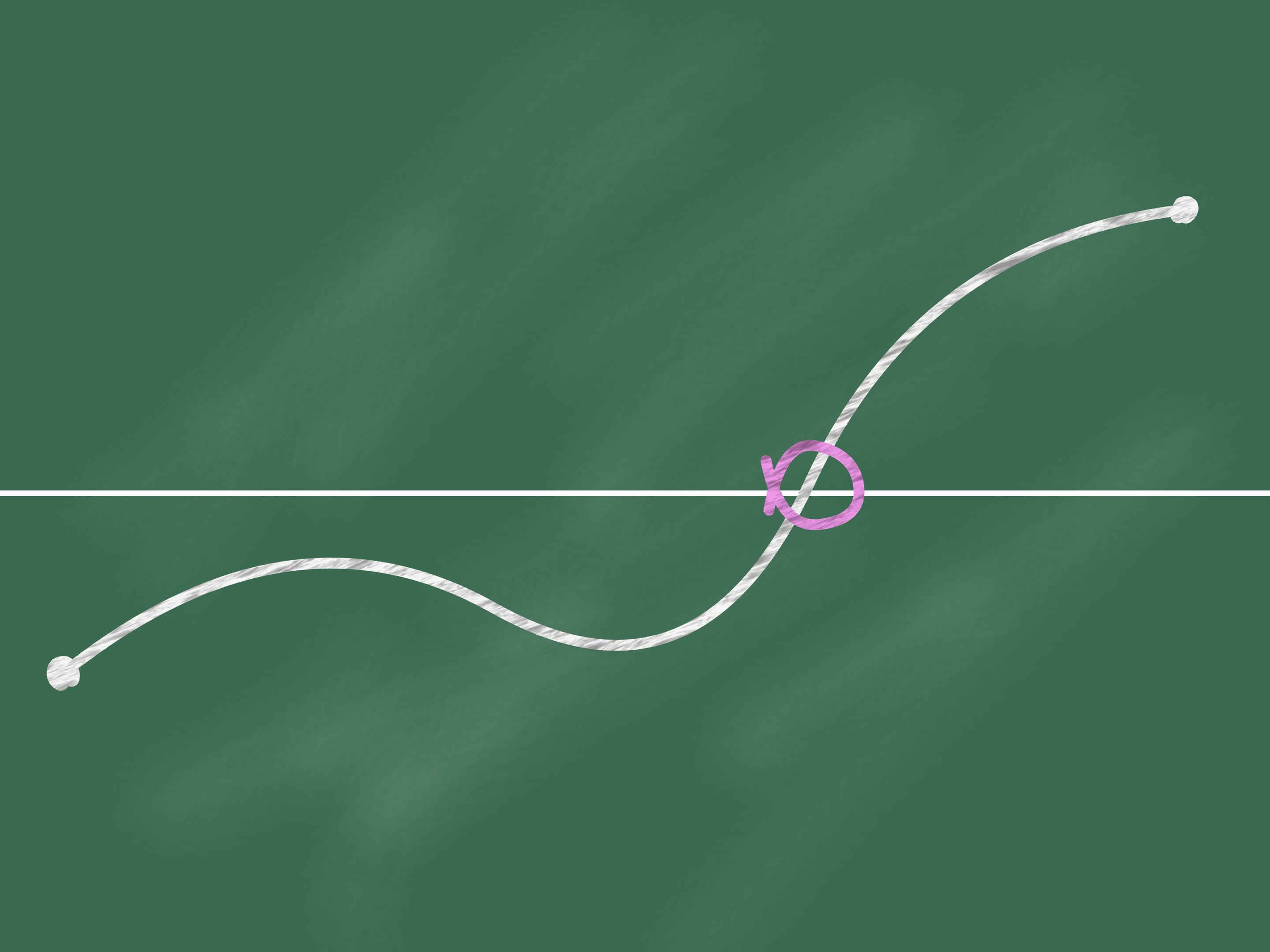
Sur le tableau noir traçons une ligne horizontale qui le divise en deux parties. Puis marquons deux points, l’un situé dans la partie en bas et l’autre dans la partie en haut.
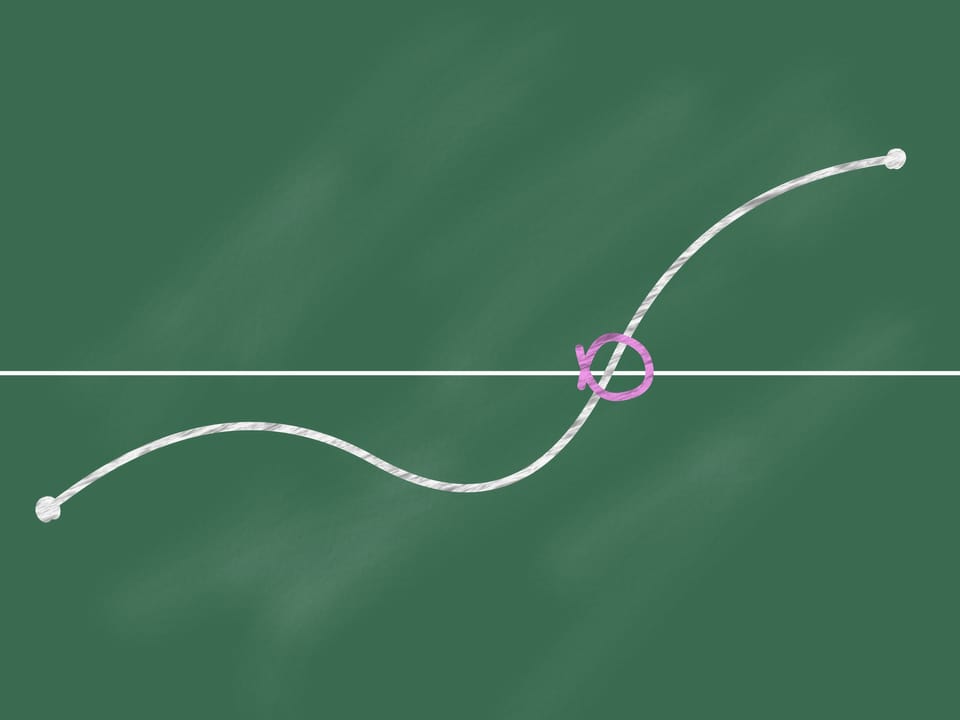
Joignons ces points par une ligne continue (c’est–à–dire ne détachant jamais la craie du tableau noir). À un certain point (qui peut être non unique) notre ligne croise la ligne horizontale.
Penseriez–vous que ce fait évident pour les enfants peut être utile en mathématiques? Malgré l’apparente évidence, cette proposition est un théorème, à savoir le théorème de Bolzano–Cauchy, et nécessite une démonstration.
Nous ne donnerons pas ici la preuve de ce théorème, mais nous observerons seulement que toutes ses hypothèses sont importantes, c’est–à–dire nécessaires. Si la ligne n’était pas continue (c’est à dire, si on pouvait détacher la craie du tableau noir), il est évident que nous pourrions sauter du bas vers le haut du tableau, sans franchir la ligne horizontale. Si on ne considérait pas l’intersection avec la ligne horizontale (qui représente l’ensemble des nombres réels), mais, par exemple, l’intersection avec seulement l’ensemble des nombres rationnels, l’intersection pouvait être évitée aussi dans ce cas.
La chose la plus surprenante c’est que cette observation en apparence enfantine est un outil très puissant utilisé dans la démonstration de certaines propositions mathématiques. L’inconvénient est que la preuve n’est pas constructive: la ligne quelque part franchit la ligne horizontale, mais à quel point exactement, étant donnée une ligne continue, il est impossible de le dire en utilisant ce théorème.
Quelques exemples de l’utilisation du théorème de Bolzano–Cauchy seront montrés dans les films de la Section “Continuité”.