Anti-Dürer ⁠

Albrecht Dürer (1471—1528) a été un grand artiste alle­mand. Il s’occu­pait de ques­tions théo­riques concer­nant les arts et, en parti­cu­lier, a étudié le problème de la pers­pec­tive. Une partie de son livre de l’année 1525 «Instruc­tions pour l’art de mesurer les figures dans le plan et dans l’espace en utili­sant règle et compas» est dédié à l’étude des propriétés des objets géomé­triques, y compris les poly­èdres et leurs déve­lop­pe­ments.

Le déve­lop­pe­ment d’un poly­èdre le long des arêtes consiste à choisir des poly­gones, disposés sur un seul plan sans qu’ils se super­posent, et des condi­tions de collage de ces poly­gones. Si en coupant un poly­èdre d’une certaine manière le long des arêtes, on obtient un seul poly­gone, en respec­tant la condi­tion de ne pas avoir de super­po­si­tions, alors ce déve­lop­pe­ment est appelé connexe.

Dans les pages de son livre Dürer montre des déve­lop­pe­ments connexes de certains poly­èdres, parfois assez compliqués. Il est peu probable qu’il s’est demandé s’il est toujours possible qu’un seul poly­gone suffit pour repré­senter le déve­lop­pe­ment d’un poly­èdre, mais la propo­si­tion qui suit prend son nom. La conjec­ture de Dürer est de supposer que chaque poly­èdre convexe a au moins un déve­lop­pe­ment connexe le long des arêtes.

Mais pour quelle raison les déve­lop­pe­ments des poly­èdres ont suscité un intérêt qui dure depuis des siècles? Le fait est que le déve­lop­pe­ment préserve en lui–même la géomé­trie interne du poly­èdre, c’est à dire, les infor­ma­tions qu’un être minus­cule, vivant sur la surface du poly­èdre et qui n’a pas de possi­bi­lité de la quitter, peut obtenir. Dans ces condi­tions de vie cet être est capable de mesurer la distance entre deux points. Utili­sant ses compé­tences en mathé­ma­tiques, il pourra aussi définir, par les mesures des distances, les angles entre deux direc­tions, et calculer l’aire d’une surface...

Pour certaines buts, l’utili­sa­tion du déve­lop­pe­ment peut être plus «commode» de l’utili­sa­tion du poly­èdre lui–même. Par exemple, si vous voulez envoyer le modèle d’un poly­èdre dans une autre ville, alors vous avez besoin d’expé­dier un colis. Mais pour envoyer le déve­lop­pe­ment du poly­èdre, il suffit d’expé­dier une lettre. Le desti­na­taire pourra construire le poly­èdre lui–même. Si vous pensez que le trans­port des poly­èdres est un procédé rare, détrompez–vous! Nous tous l’utili­sons au quoti­dien, lorsque nous ache­tons un paquet de lait ou de jus.

La conjec­ture de Dürer concerne les poly­èdres convexes. À ce jour, elle n’a été ni prouvée ni réfutée. Mais si le problème initial n’est pas de solu­tion, il vaut la peine de changer un peu les condi­tions, essayant de résoudre le problème modifié. Dans notre cas, il est naturel d’étudier la conjec­ture analogue pour une classe plus large de poly­èdres, compre­nant aussi les poly­èdres non convexes.

Il est facile de construire un poly­èdre non convexe à faces pas néces­sai­re­ment convexes, et qui n’admet aucun déve­lop­pe­ment connexe. Prenons une étoile non convexe comme base et allons construire une pyra­mide sur elle. Choi­sis­sant de façon appro­priée les angles de l’étoile et la hauteur de la pyra­mide, nous pouvons obtenir que même si une seule face laté­rale est connecté à la base dans le déve­lop­pe­ment, alors cette face se super­po­sera néces­sai­re­ment à l’étoile. Par consé­quent, la base doit être décon­necté de toutes les autres faces et le déve­lop­pe­ment n’est plus connexe.

Il n’est pas si facile d’inventer un poly­èdre non convexe avec tous les faces convexes et n’ayant aucun déve­lop­pe­ment connexe le long des arêtes. Le premier exemple a été construit seule­ment en 1999.

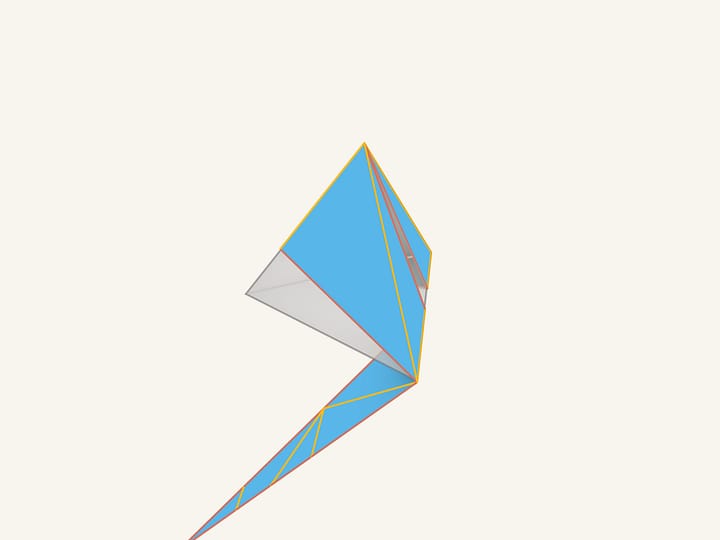
Consi­dé­rons les quatre petits tétra­èdres qui sont obte­nues en coupant un tétra­èdre régu­lier près de ses sommets. Main­te­nant on va déformer ces petites pyra­mides, en gardant leurs bases (fixées au tétra­èdre initiale) et éloi­gnant les sommets du centre du tétra­èdre; les quatre pyra­mides régu­lières résultent allon­gées. Tous les faces du poly­èdre non convexe ainsi obtenu sont des poly­gones convexes. Si les bases des pyra­mides sont assez petites par rapport à leurs hauteurs, le poly­èdre n’admet pas de déve­lop­pe­ment connexe le long des arêtes. On peut démon­trer que si le poly­èdre a un déve­lop­pe­ment connexe le long des arêtes, au moins un de ses pointes devrait admettre ce déve­lop­pe­ment, mais ce n’est pas le cas. En fait, consi­dé­rons une «pointe» avec des morceaux des faces du poly­èdre qui lui sont connectés. Tous les déve­lop­pe­ments possibles le long des arêtes de cette partie du poly­èdre, constitué d’un seul morceau, auront des super­po­si­tions.

Main­te­nant que nous avons vu un «contrexemple non–convexe» à la conjec­ture de Dürer, nous reve­nons à sa formu­la­tion initiale, dans la classe des poly­èdres convexes.

Le plus simple des poly­èdres convexes c’est la pyra­mide trian­gu­laire (ou tétra­èdre), qui a quatre sommets et quatre faces.

Mais même dans cette classe plus simple des poly­èdres, il existe de repré­sen­tants pour lesquels pas tous les déve­lop­pe­ments le long des arêtes sont sans super­po­si­tions. Cepen­dant, tous ces repré­sen­tants admettent des déve­lop­pe­ments connexes. Jusqu’à présent, on n’a pas construit aucun poly­èdre, ayant déve­lop­pe­ments le long des arêtes avec super­po­si­tions, et constitué d’un seul morceau.

Il n’y a pas long­temps N. P. Dolbinin a formulé une conjec­ture nouvelle, qu’il a appelé «anti–Durer». Etant donné un entier $k$ arbi­traire, il existe un poly­èdre convexe tel que, pour que son déve­lop­pe­ment sur le plan le long des arêtes soit sans super­po­si­tions, il doit être divisé au moins en $k$ morceaux.

Nous obser­vons que si la conjec­ture de Dürer est fausse, alors il ya deux cas sensi­ble­ment diffé­rents.

Le cas borné: pour tout poly­èdre convexe il y a un déve­lop­pe­ment sans super­po­si­tions constitué au plus de $k$ morceaux. Dans ce cas le nombre $k$ mini­male est le même pour toutes les classes de poly­èdres convexes, et il ne dépend pas des cas concrets parti­cu­liers.

Plus inté­res­sant c’est le cas non borné: dans la classe de tous les poly­èdres, le nombre de morceaux néces­saires n’est pas supé­rieu­re­ment borné.

La conjec­ture «anti–Dürer» consiste seule­ment à supposer que nous ne sommes pas dans le cas borné.

Récem­ment, son analogue dans le cas des poly­èdres non convexes (dans le cas non borné) a été démontré par des mathé­ma­ti­ciens russes.

Vous pouvez essayer de construire un poly­èdre convexe, pour lequel tout déve­lop­pe­ment connexe le long des arêtes a des super­po­si­tions, ou de démon­trer que ce poly­èdre n’existe pas. Et, si vous réus­sissez, une belle nouvelle page sera ajoutée à la géomé­trie.