Une coupe ⁠

Sur une feuille de papier, on a dessiné un poly­gone spontané. Pour­rions-nous plier la feuille de papier afin de découper le poly­gone en une coupe droite linéaire.

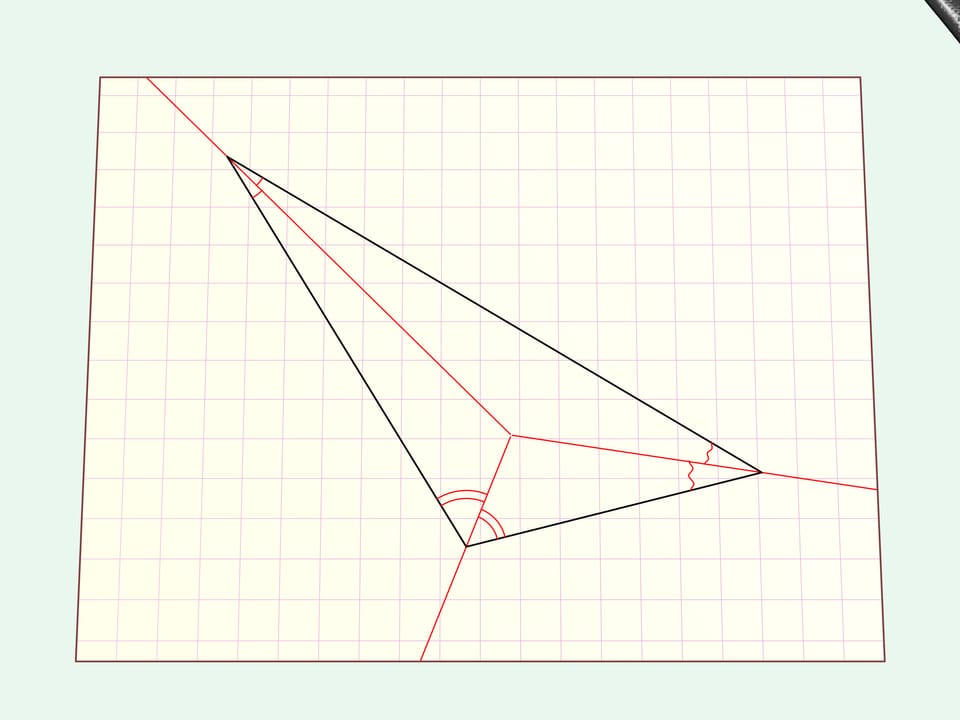
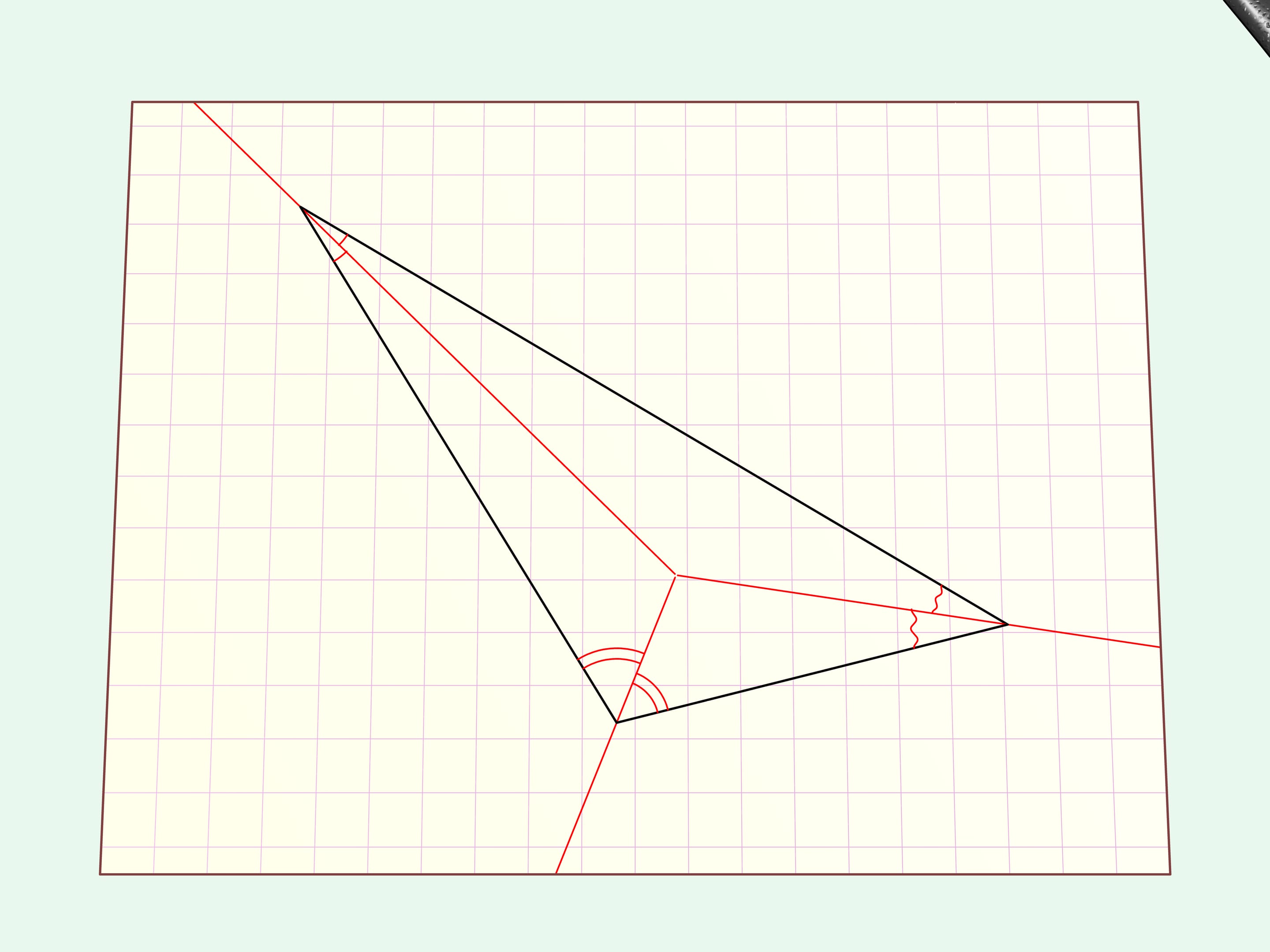
Exami­nons le cas le plus simple: un triangle quel­conque.

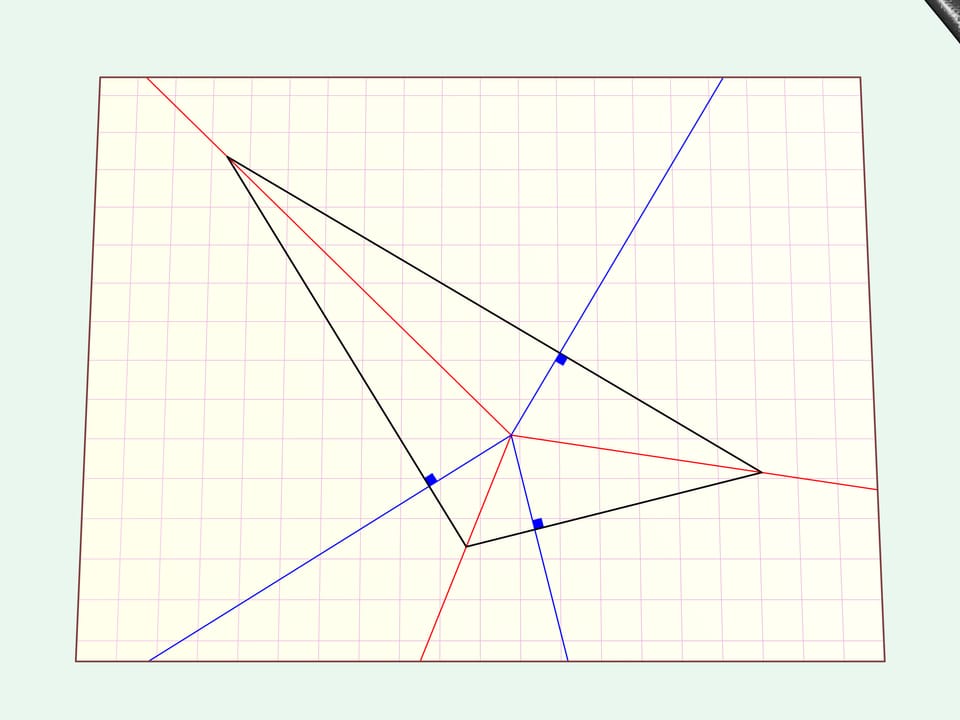
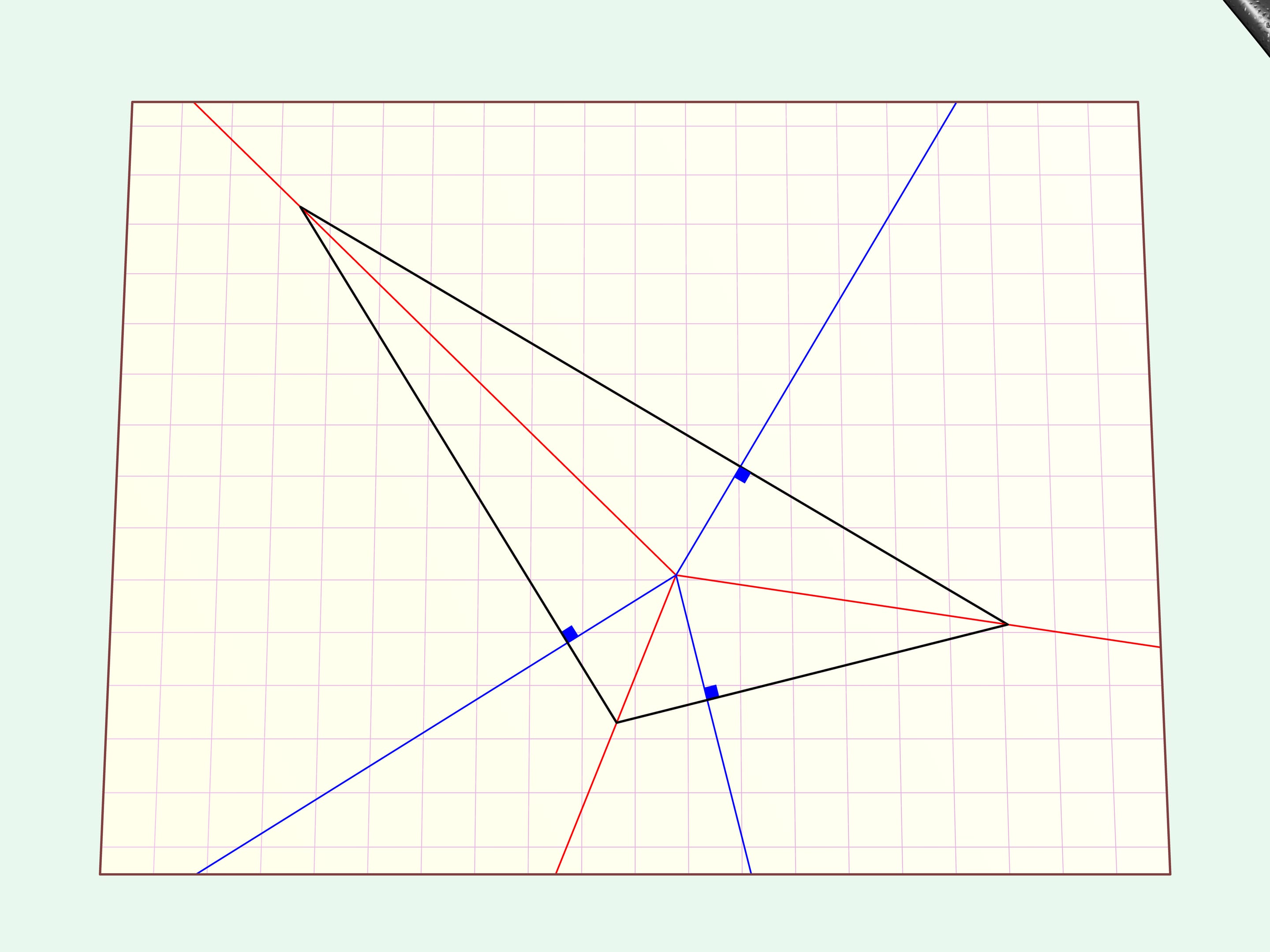
Traçons des bissec­trices et, du point de leur inter­sec­tion, créons des perpen­di­cu­laires sur un côté du triangle.

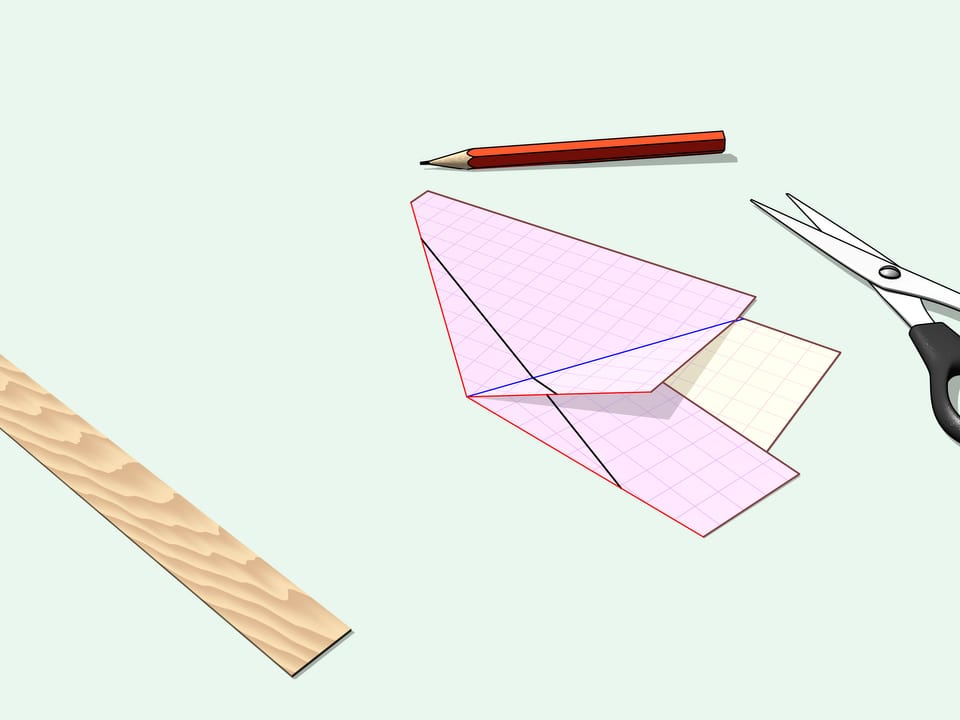
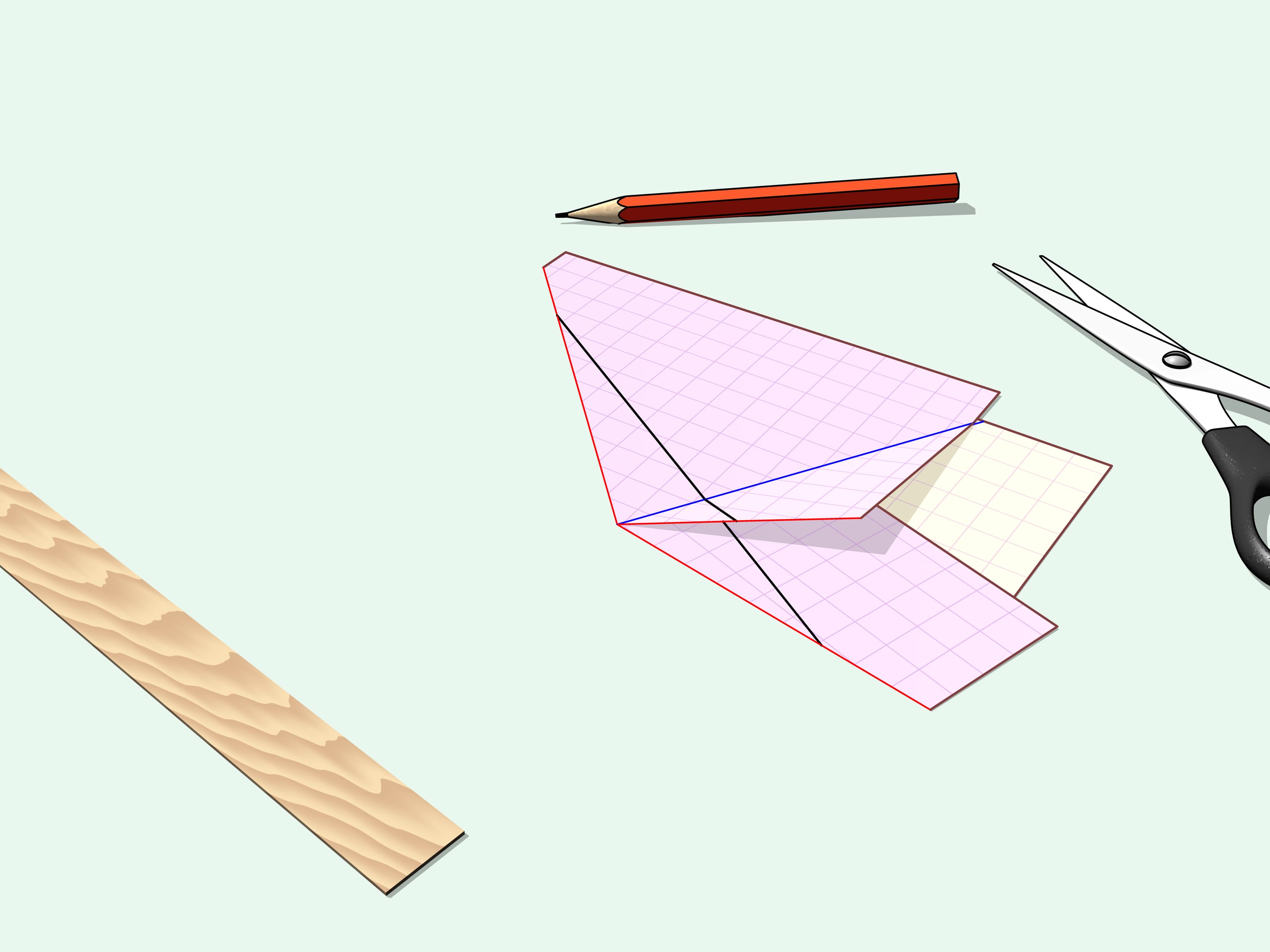
Plions la feuille de papier selon ces tracés. Toutes les limites du triangle, ses côtés, paraissent alignés sur une seule droite. Faisons une coupe linéaire droite le long de celle-ci.

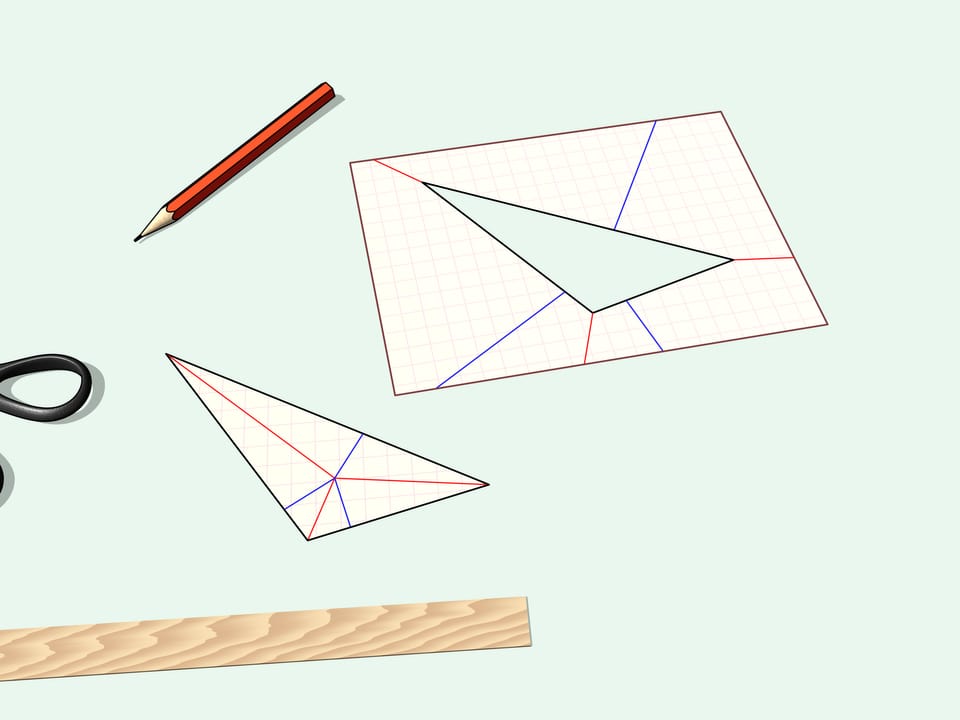
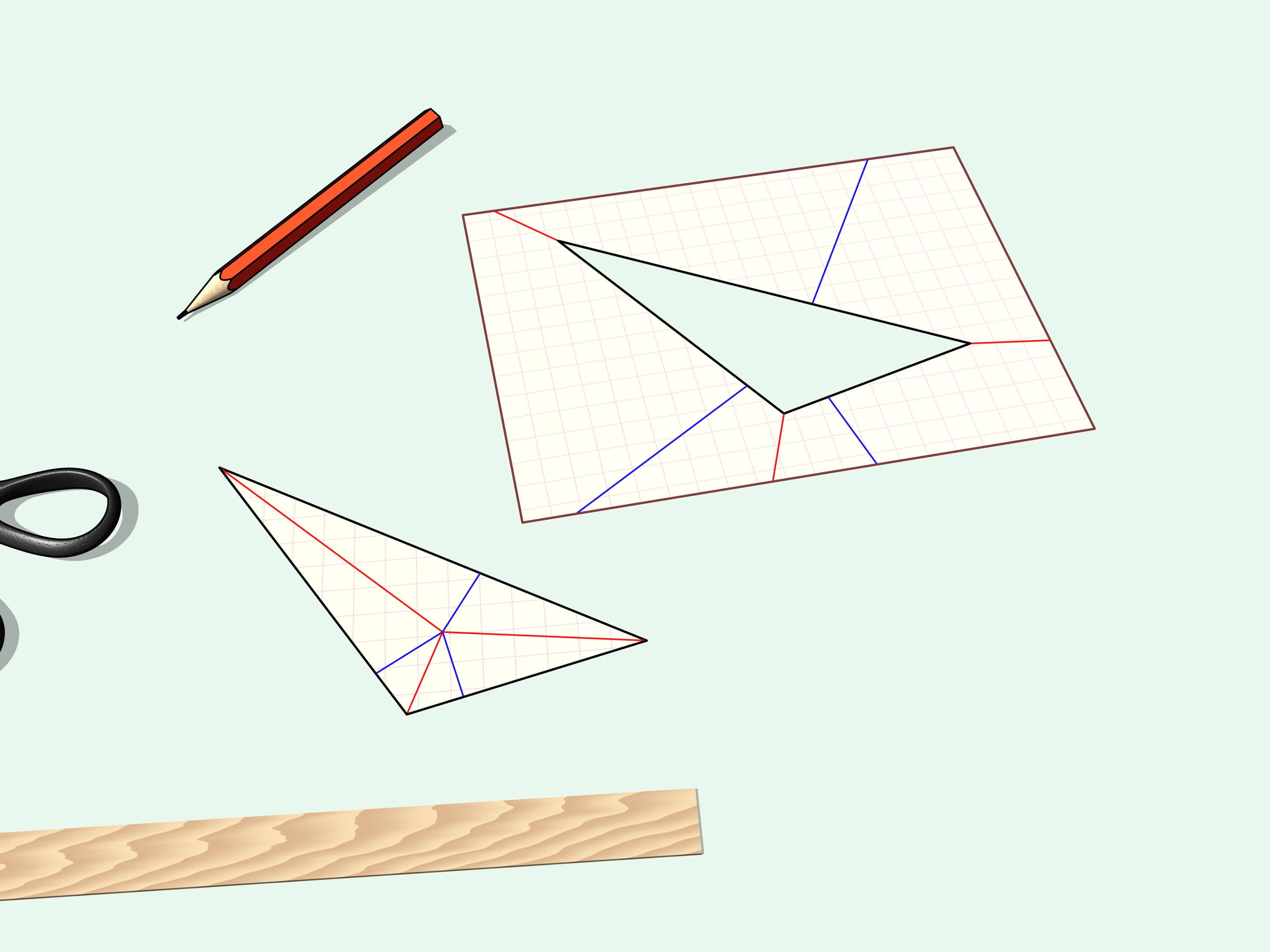
Plions l’angle coupé, c’est notre triangle de départ. Si on plie la partie de feuille restante, on verra alors que rien de superflu n’a été coupé. Le trou ressemble égale­ment au triangle de départ.

Dessi­nons une étoile à cinq branches. C’est un poly­gone concave à dix côtés.

Cepen­dant, dans ce cas, l’exer­cice se simplifie avec la symétrie de l’étoile. Traçons des rayons partant du centre et passant par les sommets.

Plions la feuille de papier selon ces rayons. Coupons l’angle. Après le dépliage, nous obtien­drons une étoile découpée et un trou ressem­blant à une étoile.

Le poly­gone dessiné au début du film peut égale­ment être découpé de façon linéaire droite.

En 1998, un théorème commun a été démontré. On peut toujours plier une feuille de papier de façon à ce que n’importe quel poly­gone, dessiné dessus, soit une coupe linéaire droite.

La démons­tra­tion du théorème est algo­rith­mique, c’est-à-dire que les auteurs mènent à un moyen de plier la feuille de papier pour que le poly­gone dessiné concrètement puisse être découpé d’une coupe linéaire droite.