Le chemin plus court ⁠

Notre planète, la Terre, a la forme d’une sphère légèrement aplatie aux pôles. Depuis assez de temps les hommes utilisent un globe à forme de sphère pour représenter la terre. Mais un moyen encore plus ancien de représenter la surface de la terre est la carte géogra­phique.

La sphère est une surface à cour­bure posi­tive constante, et pour cette raison il n’est pas possible de la représenter sur un plan sans distor­sion. Les façons de construire les cartes géogra­phiques, c’est–à–dire les projec­tions carto­gra­phiques, ont une histoire longue et très intéressante. Certains de ces moyens sont plus fami­liers à nous, d’autres ne sont utilisés que dans des situa­tions parti­culières, et plus rare­ment on les rencontre dans la vie quoti­dienne, mais ce sujet nécessite par lui même un autre film.

Autre­fois en Russie il y avait une excel­lente tradi­tion d’accro­cher une carte du monde dans la cuisine ou dans la chambre des enfants. A’ toute nouvelle on attri­buait immédiate­ment visuel­le­ment un lieu géogra­phique spécifique.

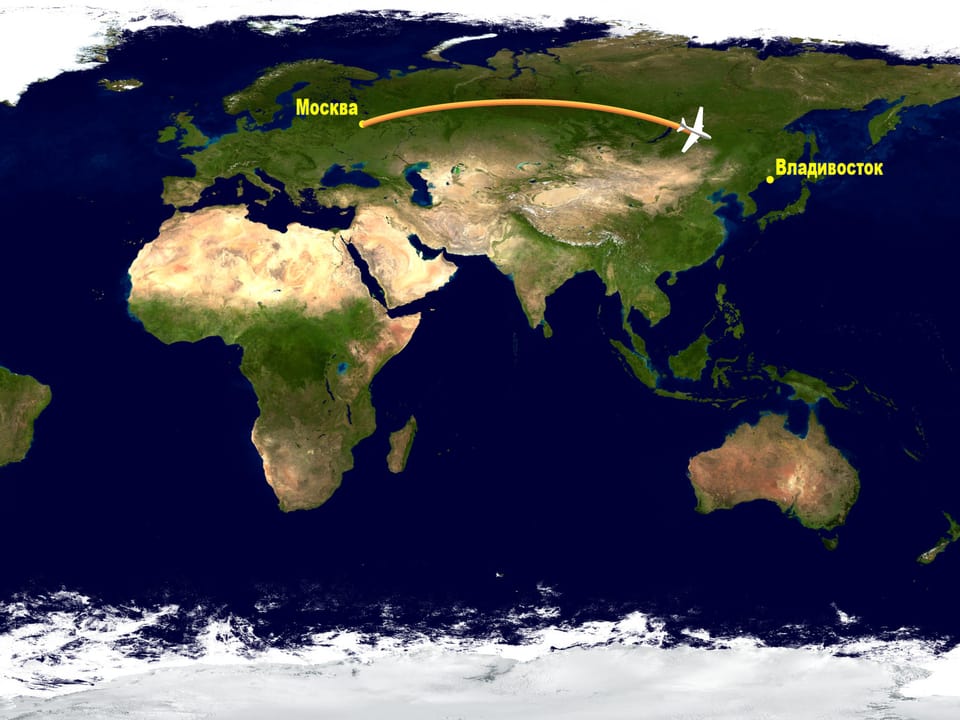
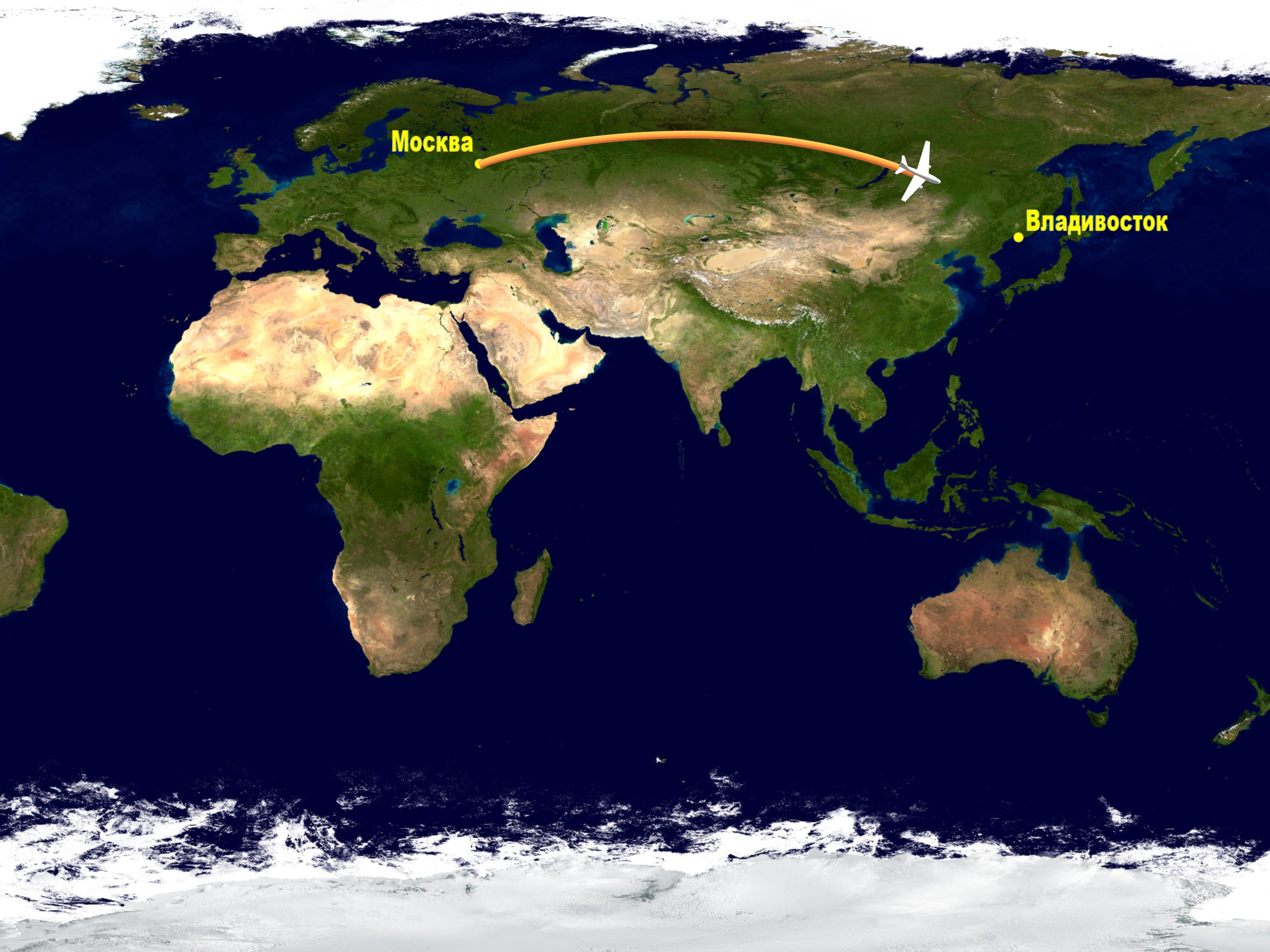
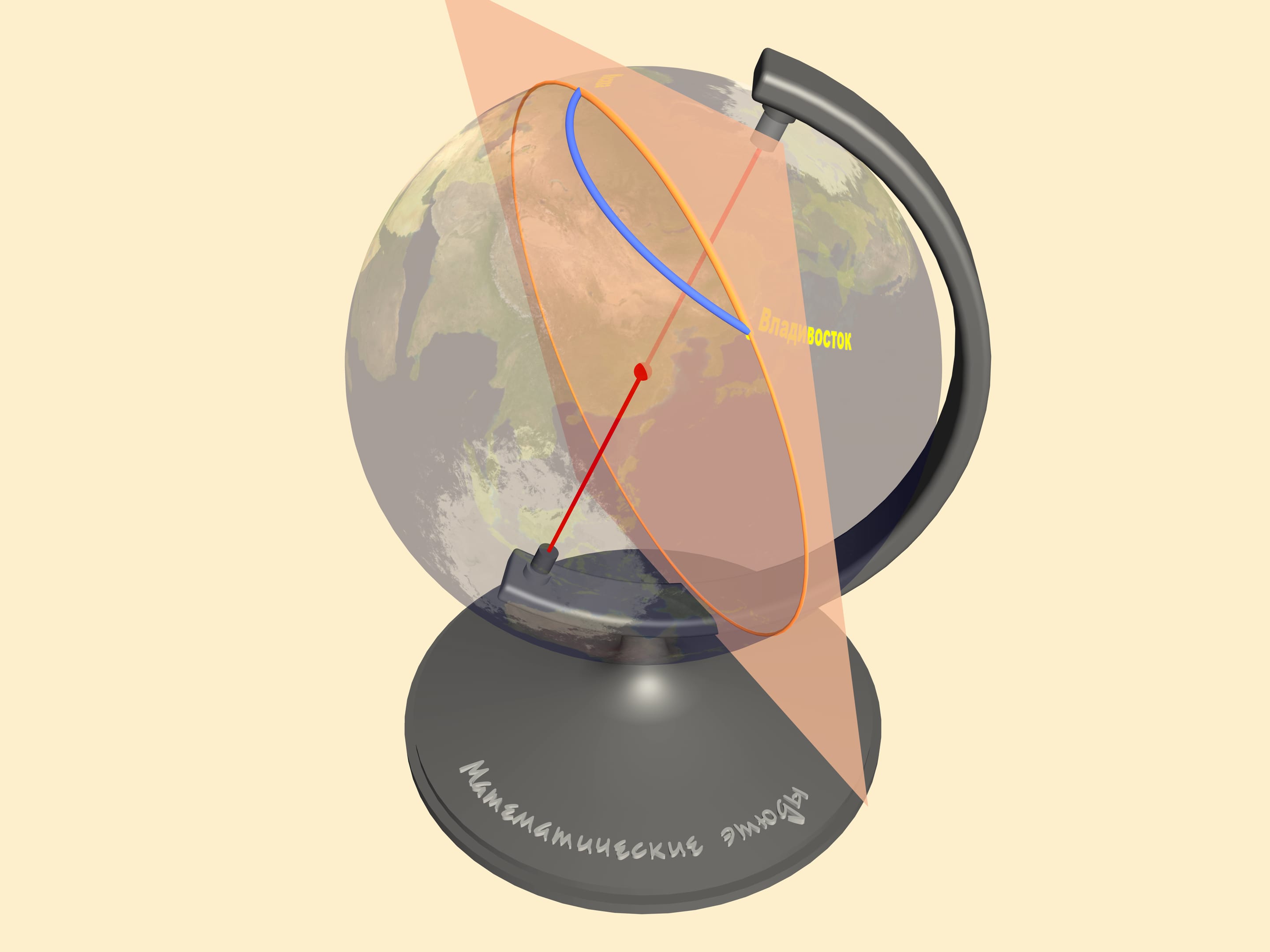
Regar­dons une carte, obtenue par une des projec­tions stan­dard, et tirons sur elle la route faite par les avions qui volent de Moscou à des villes orien­tales de la Russie, par exemple, à Vladi­vostok. Si vous avez fait ce parcours quelques fois, vous avez sûrement remarqué que sur la carte la route de l’avion passe très haut.

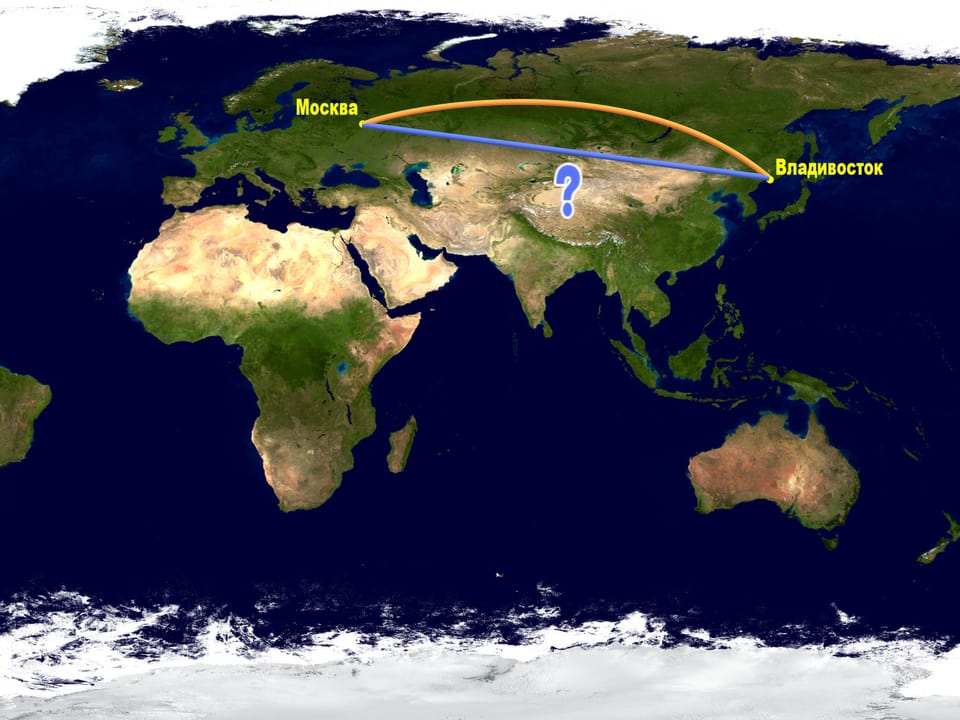
Les vols d’avions, tout le monde sait qu’ils sont très coûteux. Alors pourquoi choisir de voler le long d’un arc simi­laire, quand on pour­rait voler le long d’une route plus courte, ce qui corres­pond à une ligne droite sur la carte?

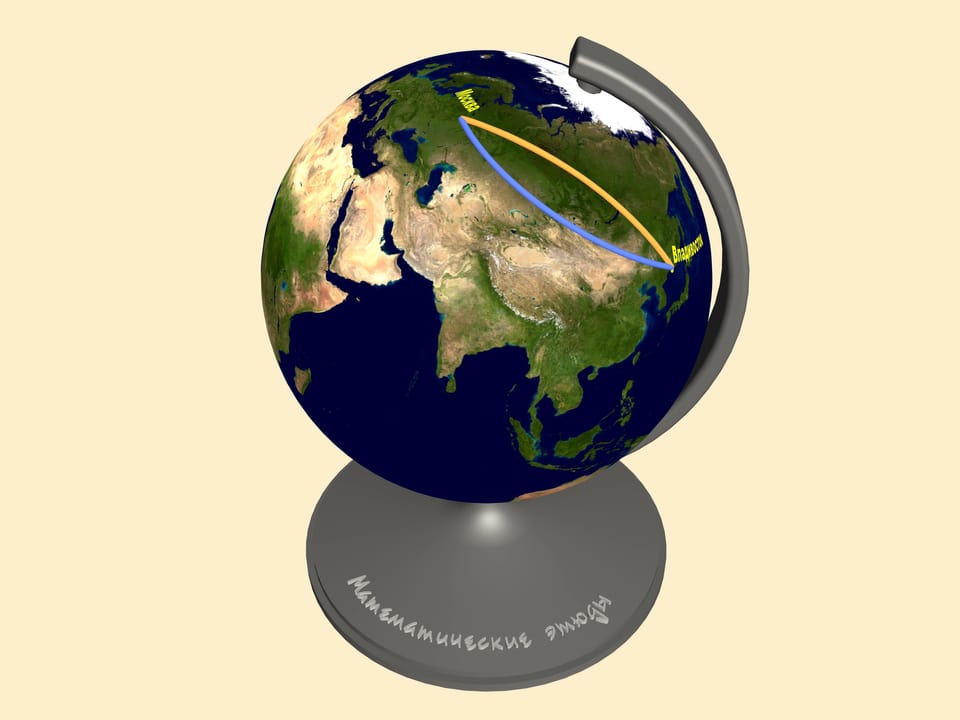
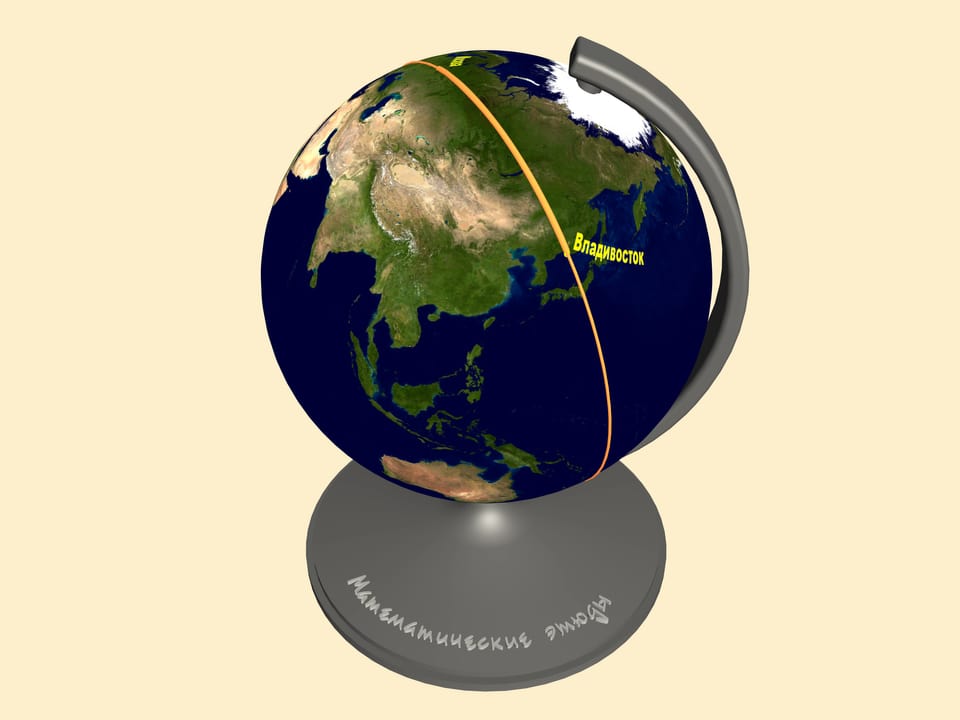
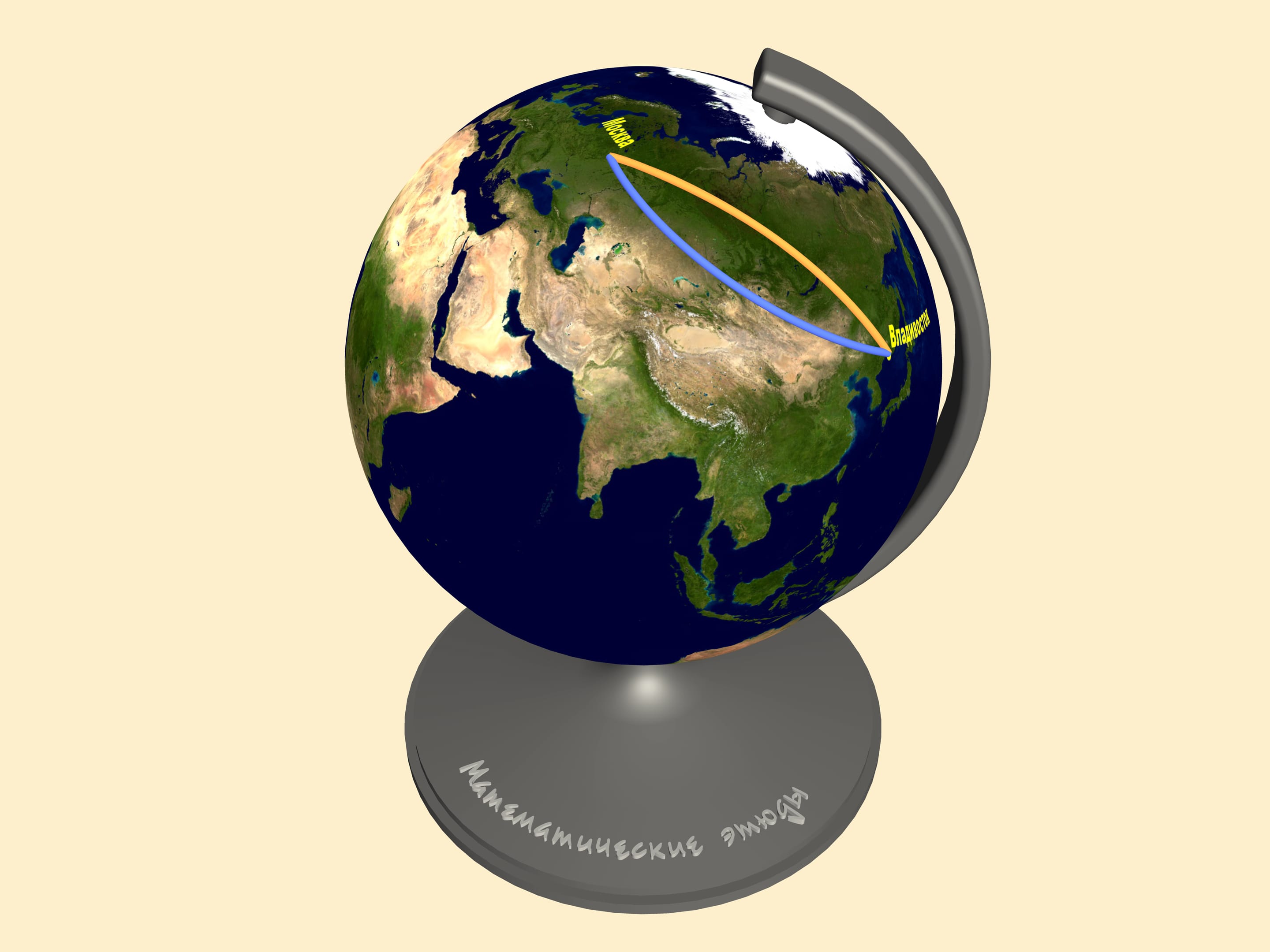
Le problème est que le concept de la distance la plus courte est intrinsèquement liée à la surface où la distance est mesurée. Comme déjà noté, toute carte plaine de la surface de la Terre est déformé. Obser­vons la trajec­toire corres­pon­dante sur le globe. Seule­ment main­te­nant nous pouvons mesurer la longueur des routes en ques­tion.

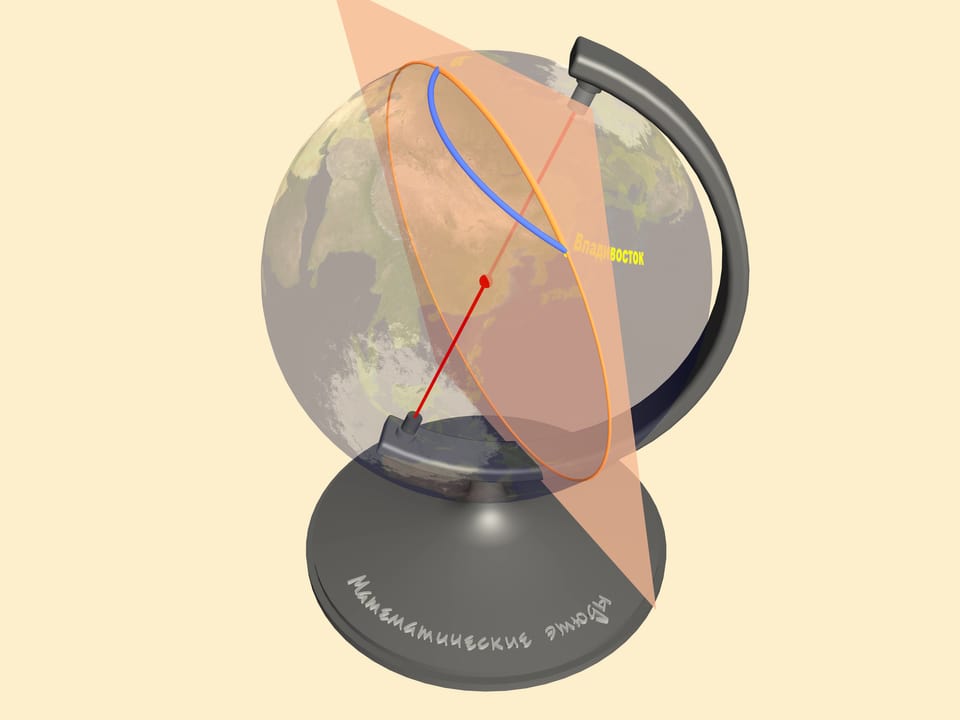
Pour trouver la distance plus courte entre deux points sur une sphère, il faut faire passer un grand cercle à travers eux. C’est le cercle formé par l’inter­sec­tion de la sphère avec le plan passant par le centre de la sphère et les deux points. La distance mini­male entre deux points sur la sphère est alors la longueur du minimum de deux arcs de grand cercle reliant les deux points. Cet arc est unique, si les deux ne sont pas des points diamétrale­ment opposés sur la sphère. En mathématiques, une ligne corres­pon­dant à la distance mini­male entre deux points sur une surface est appelée une géodésique.

Tous les autres chemins qui relient Moscou à Vladi­vostok, y compris ce qui semblait être tout droit sur la carte, seront plus longs que cet arc!

Comme nous l’avons vu, les avions volent exac­te­ment le long des arcs de grands cercles, c’est à dire le long des routes les plus courtes.