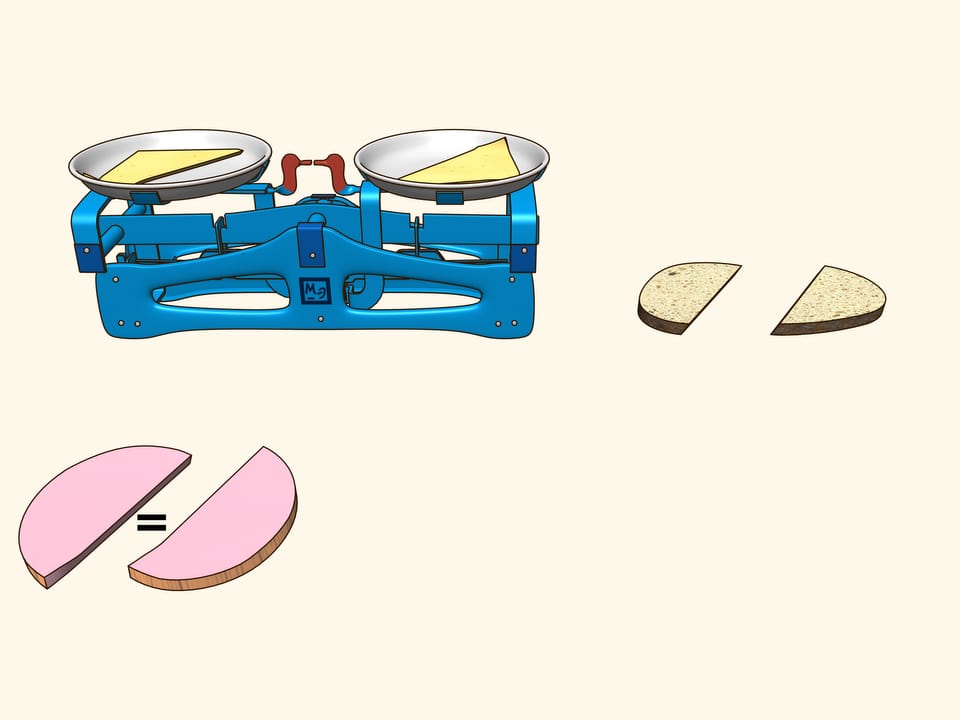
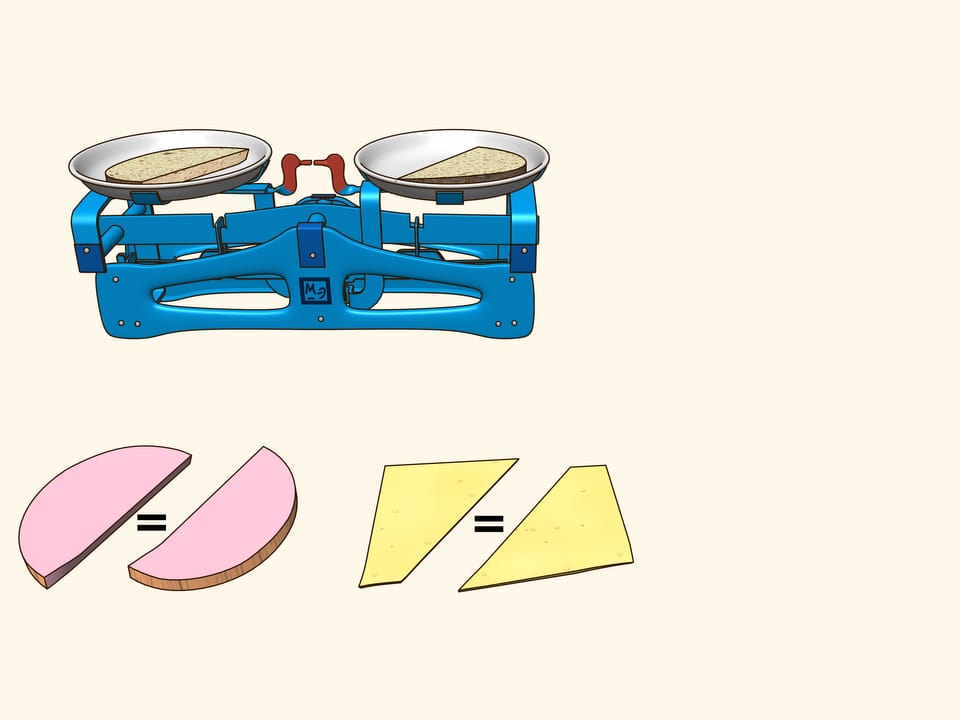
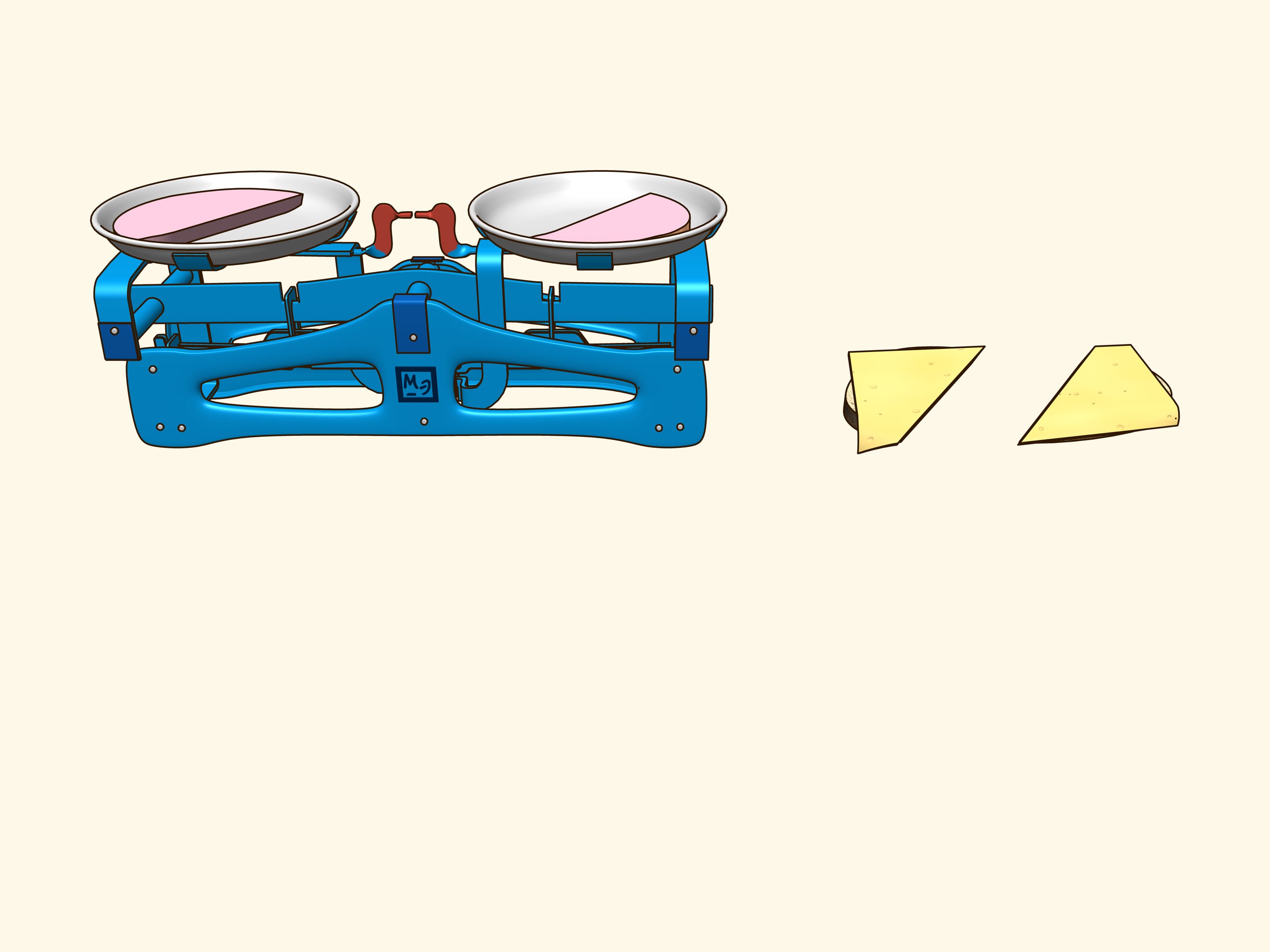
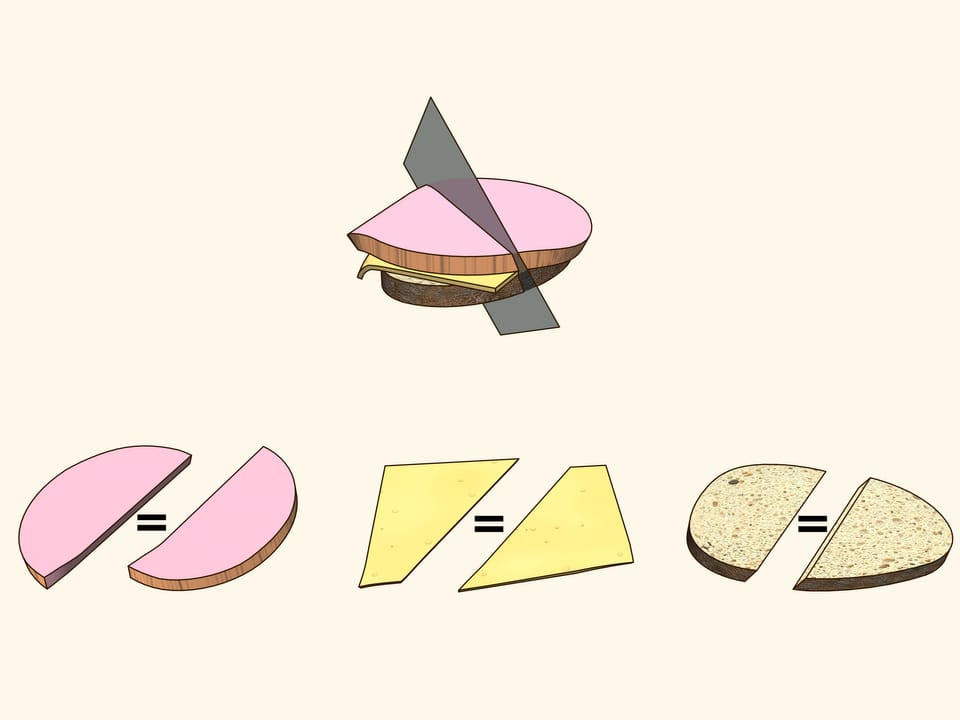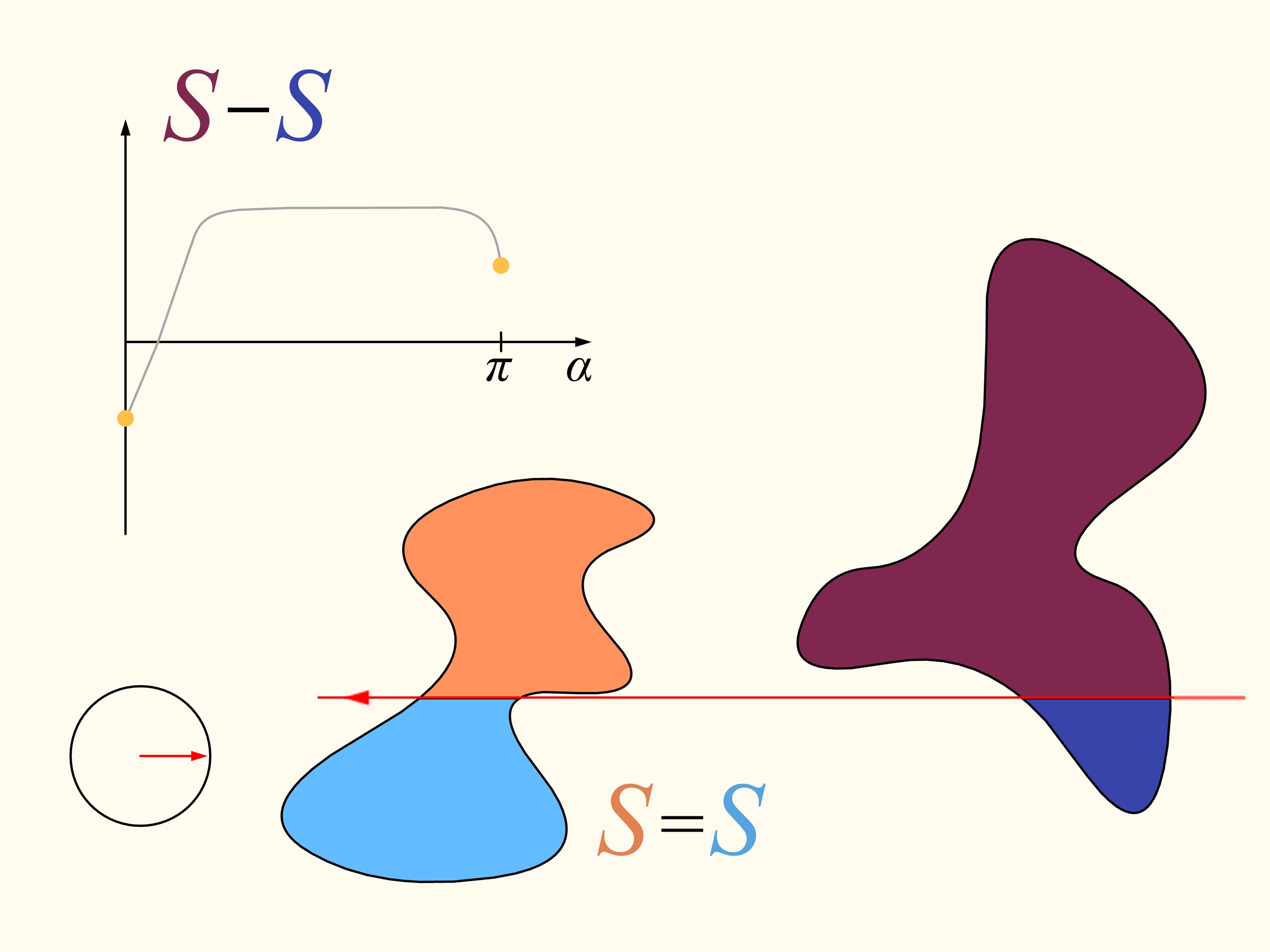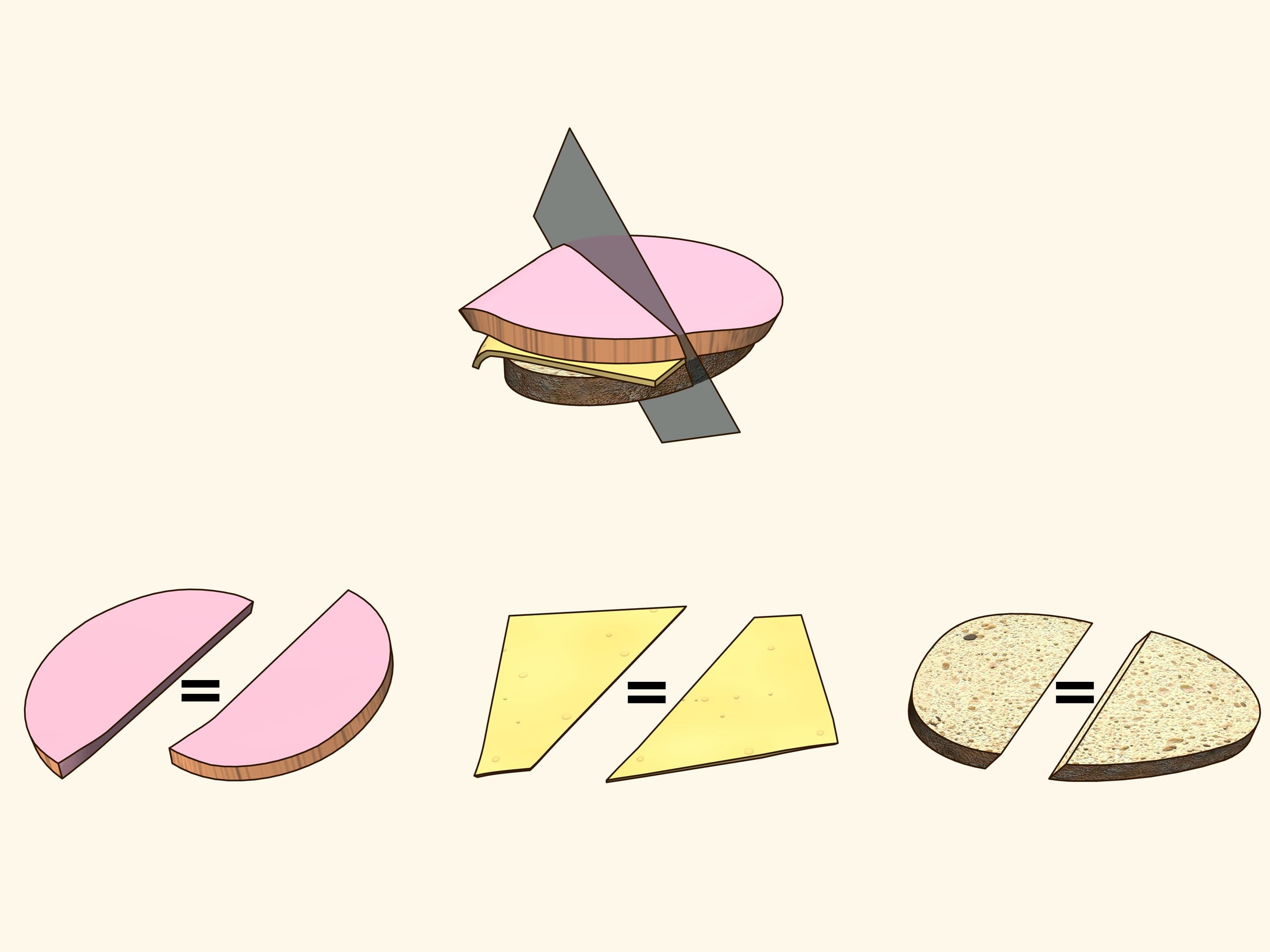Est–ce que l’on peut couper par une section planaire un sandwich fait d’une tranche de pain, une de fromage et une de jambon d’une manière que les deux parties contiennent les mêmes quantités de pain, de fromage et de jambon? Nous allons montrer qu’il est possible.
Considérons d’abord le problème à deux dimensions. Supposons qu’on a fixé deux régions dans le plan. Y a–t–il une droite qui divise simultanément la première à la seconde région en deux parties de la même aire?
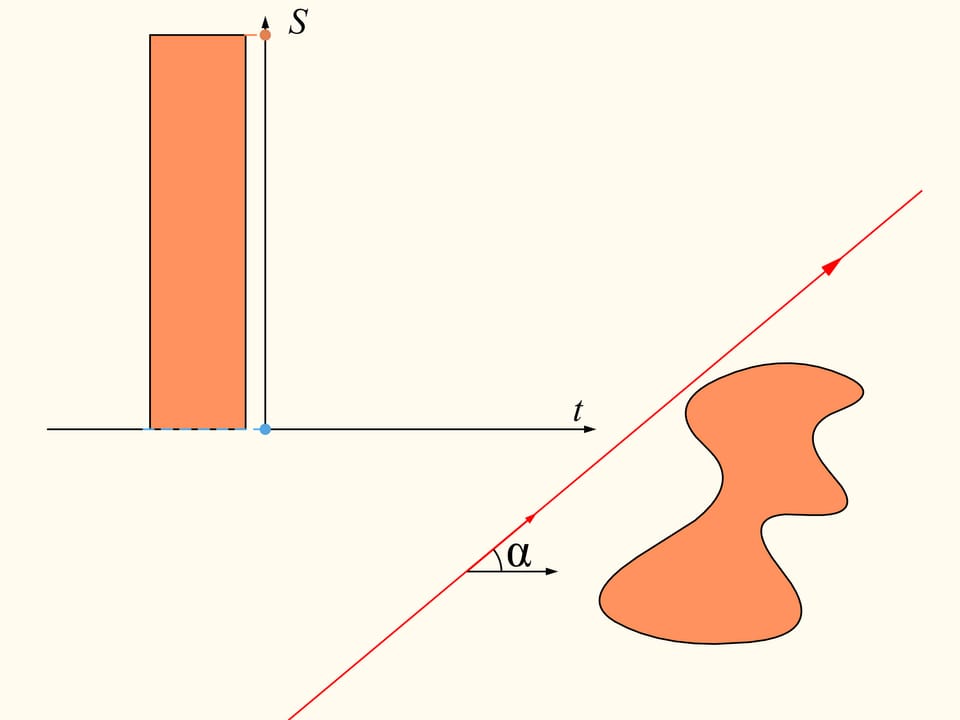
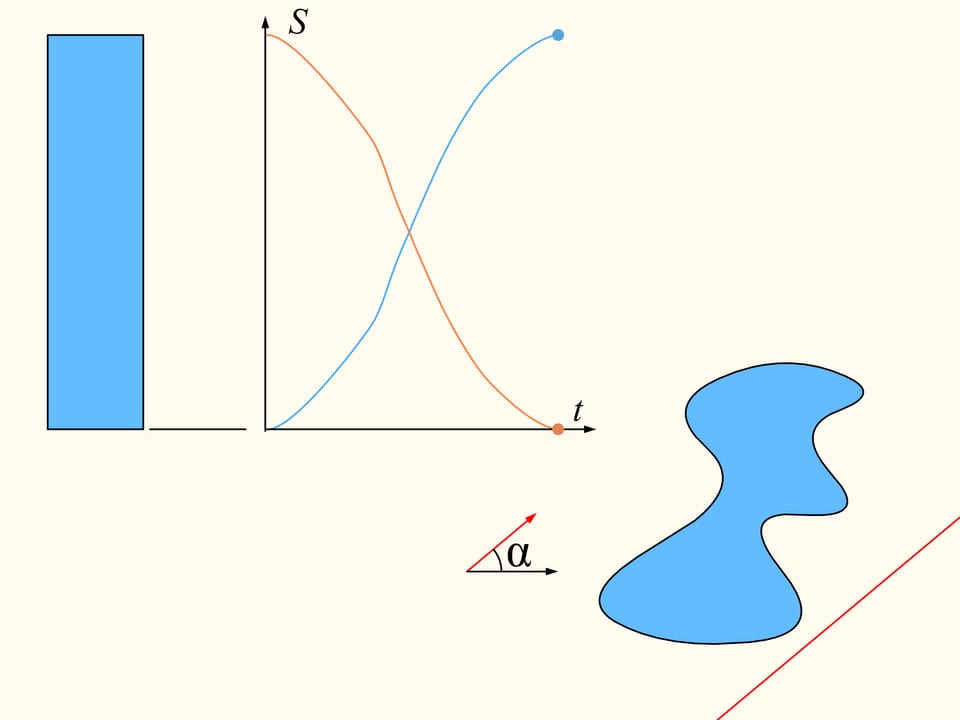
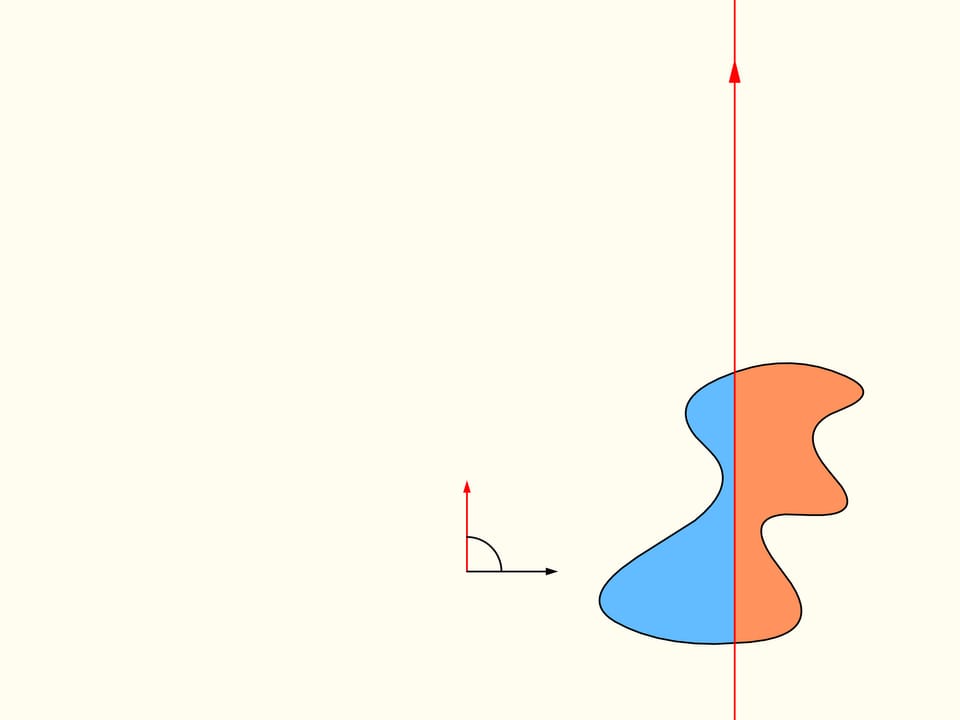
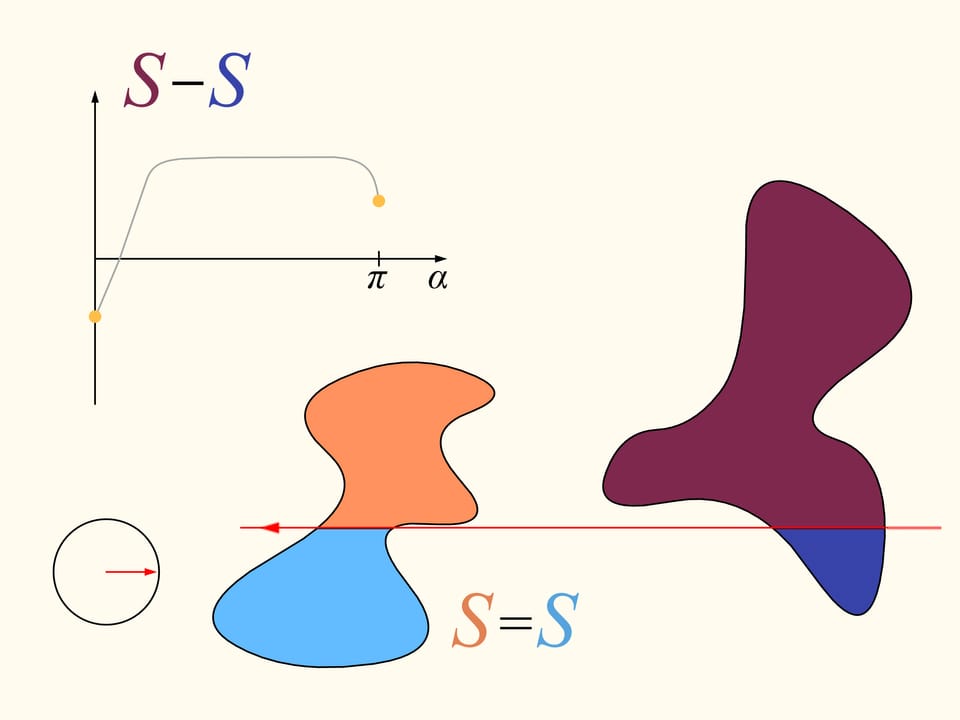
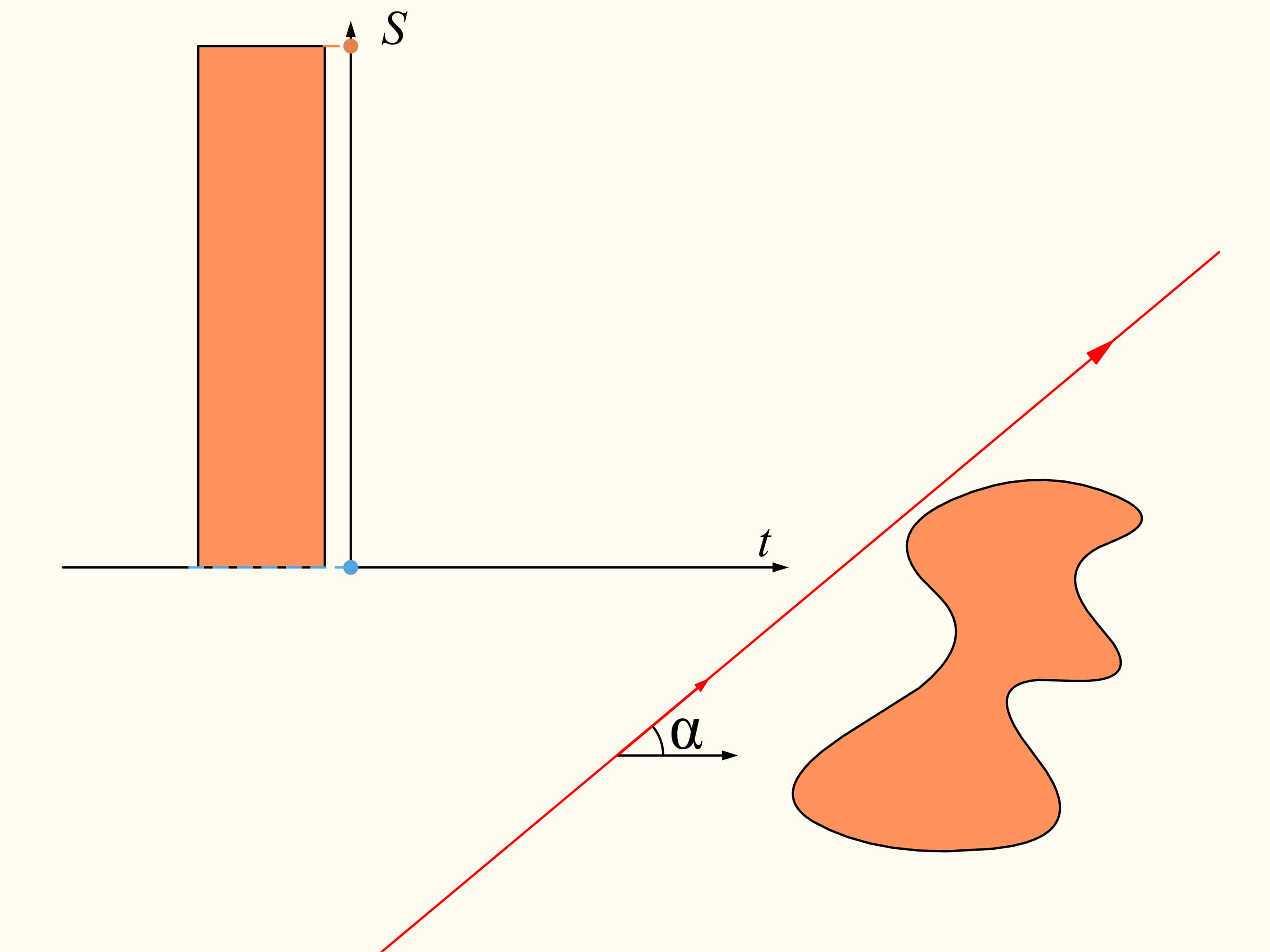
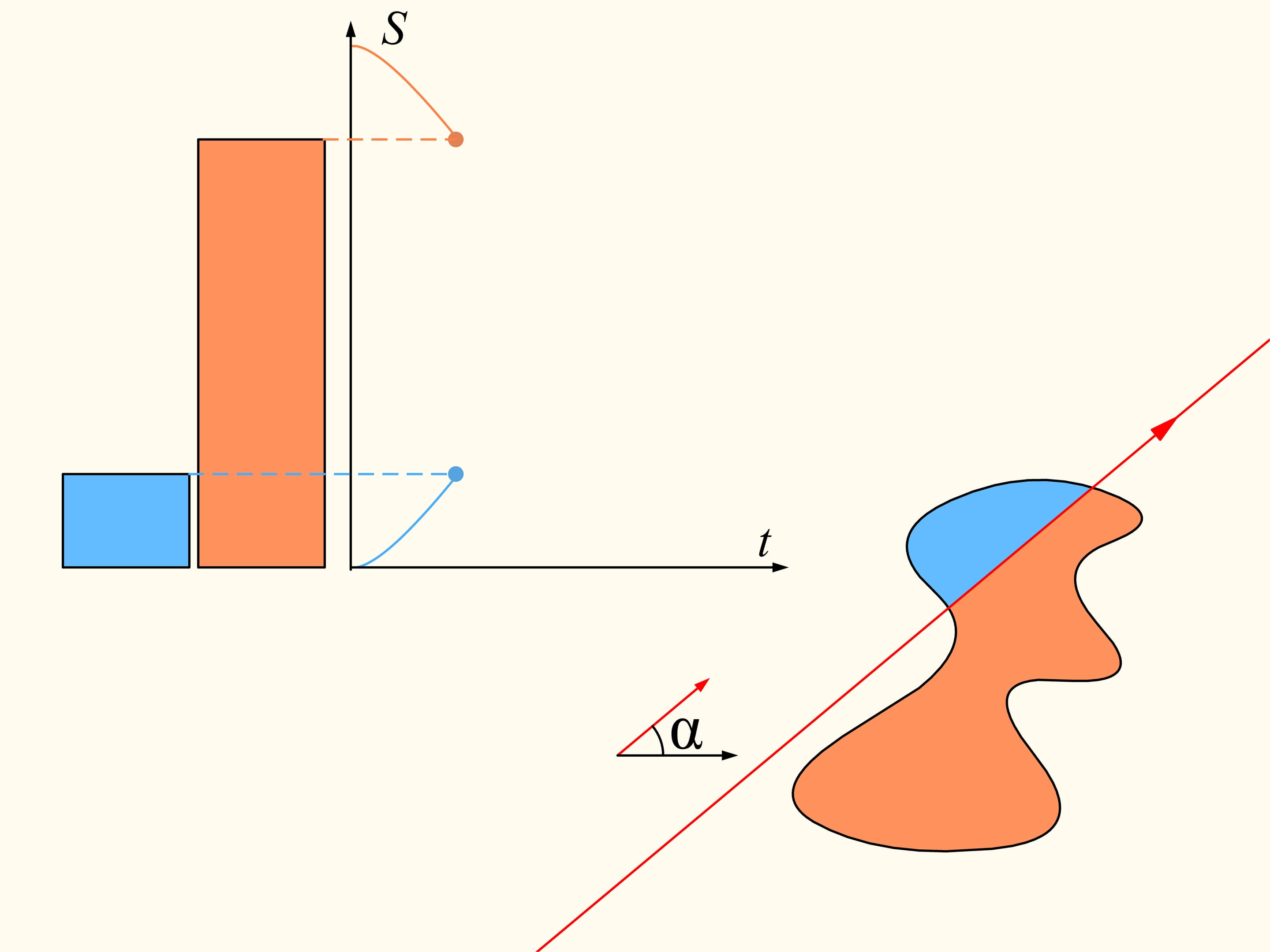
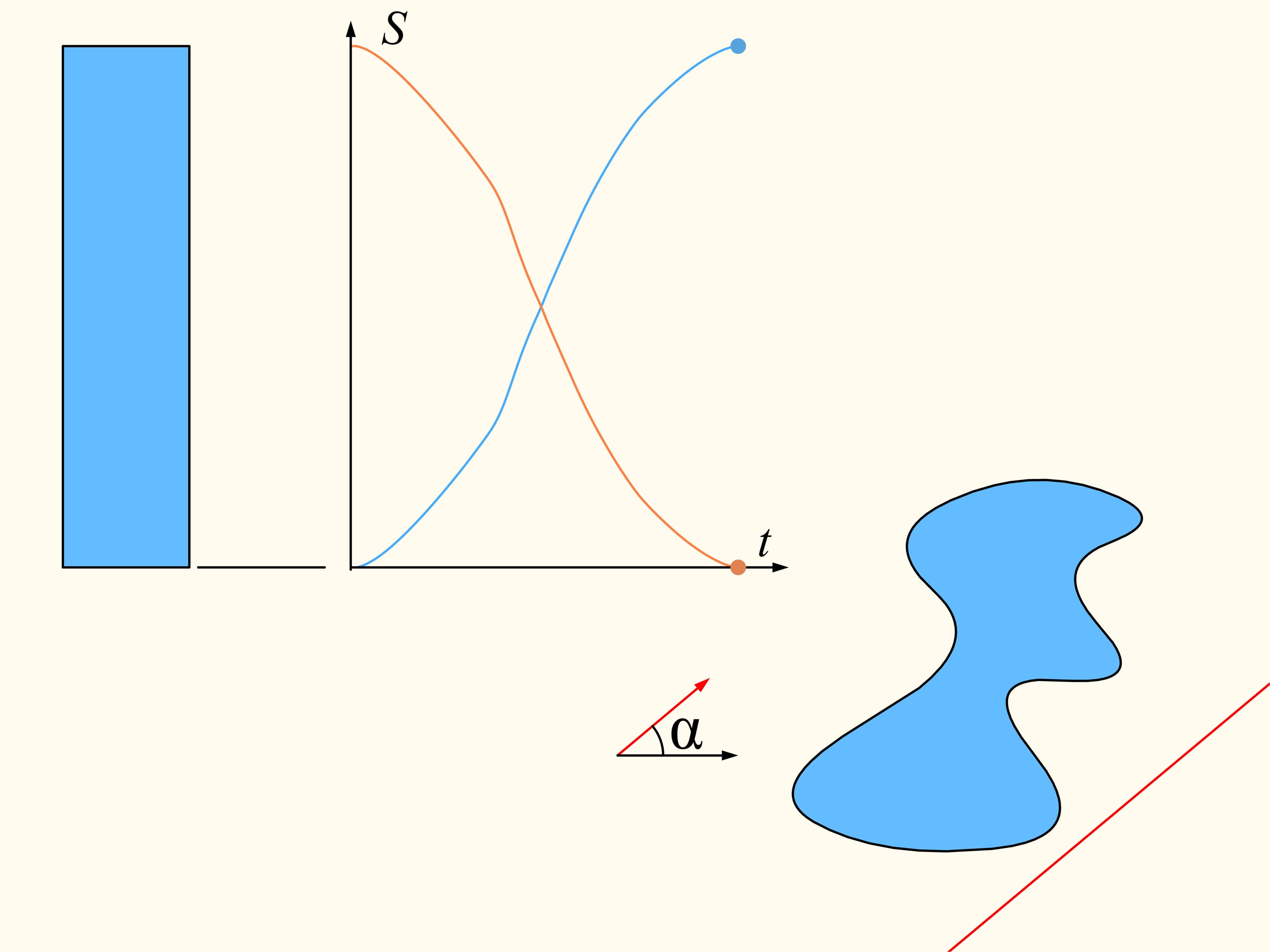
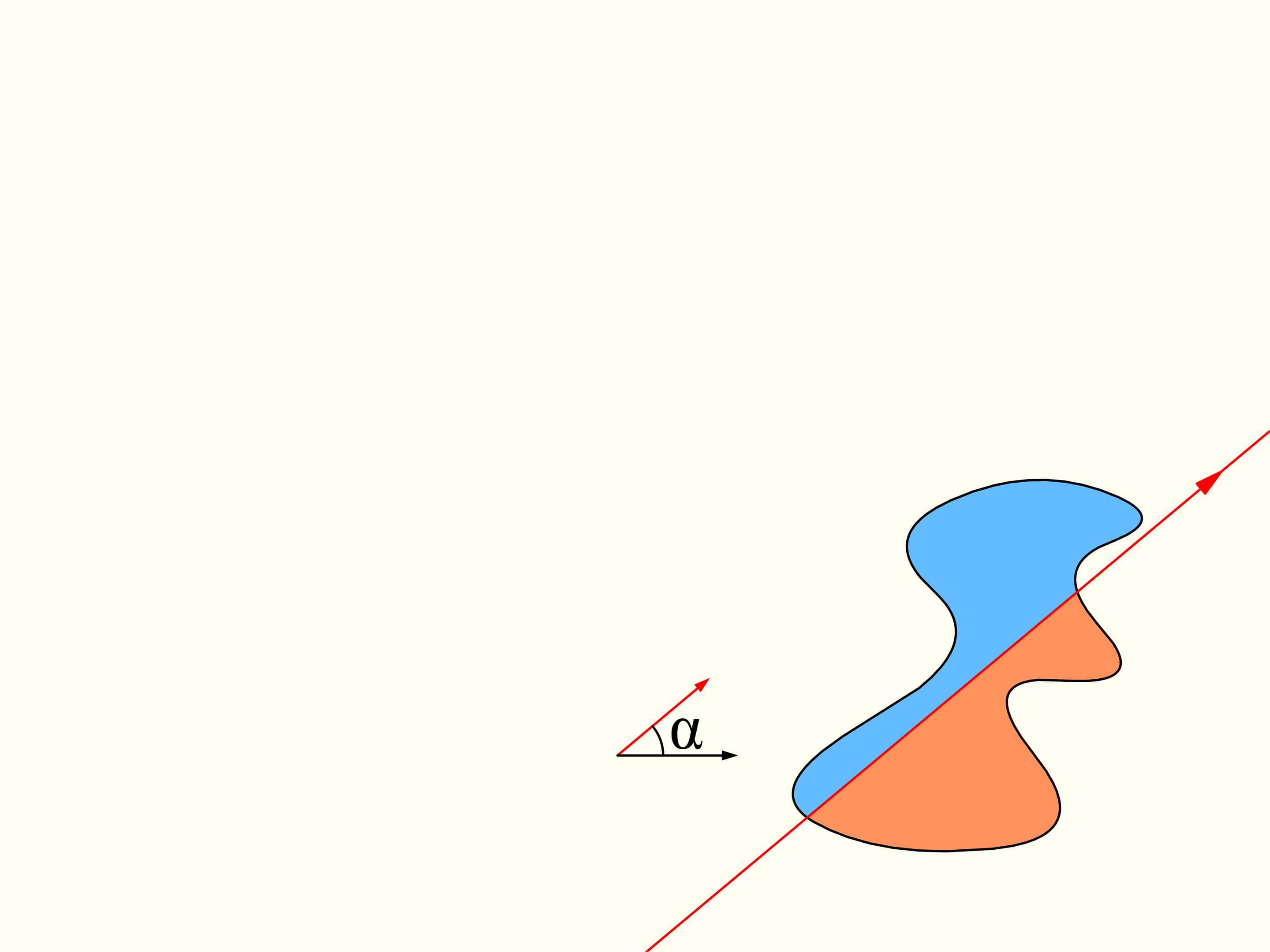
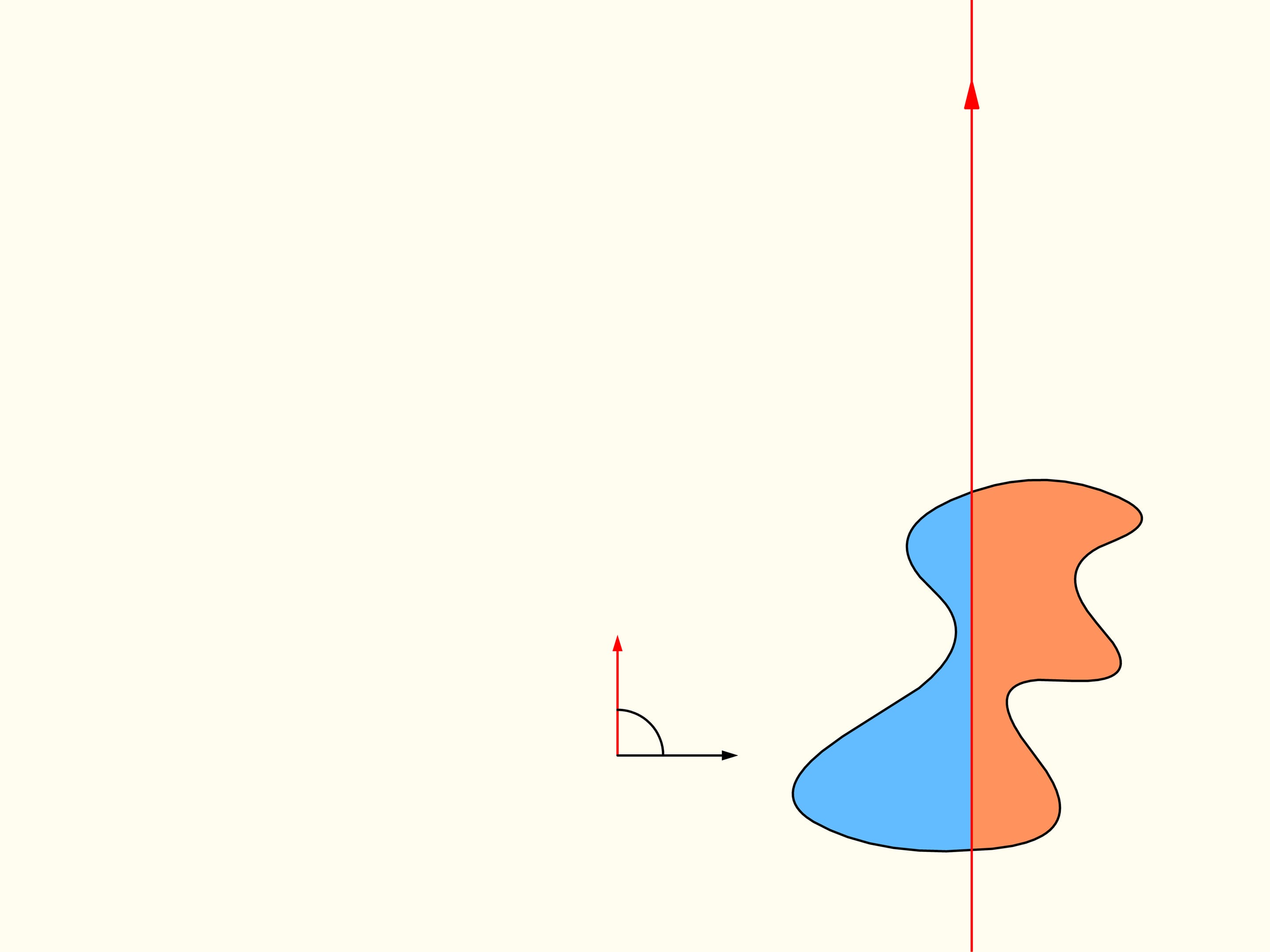
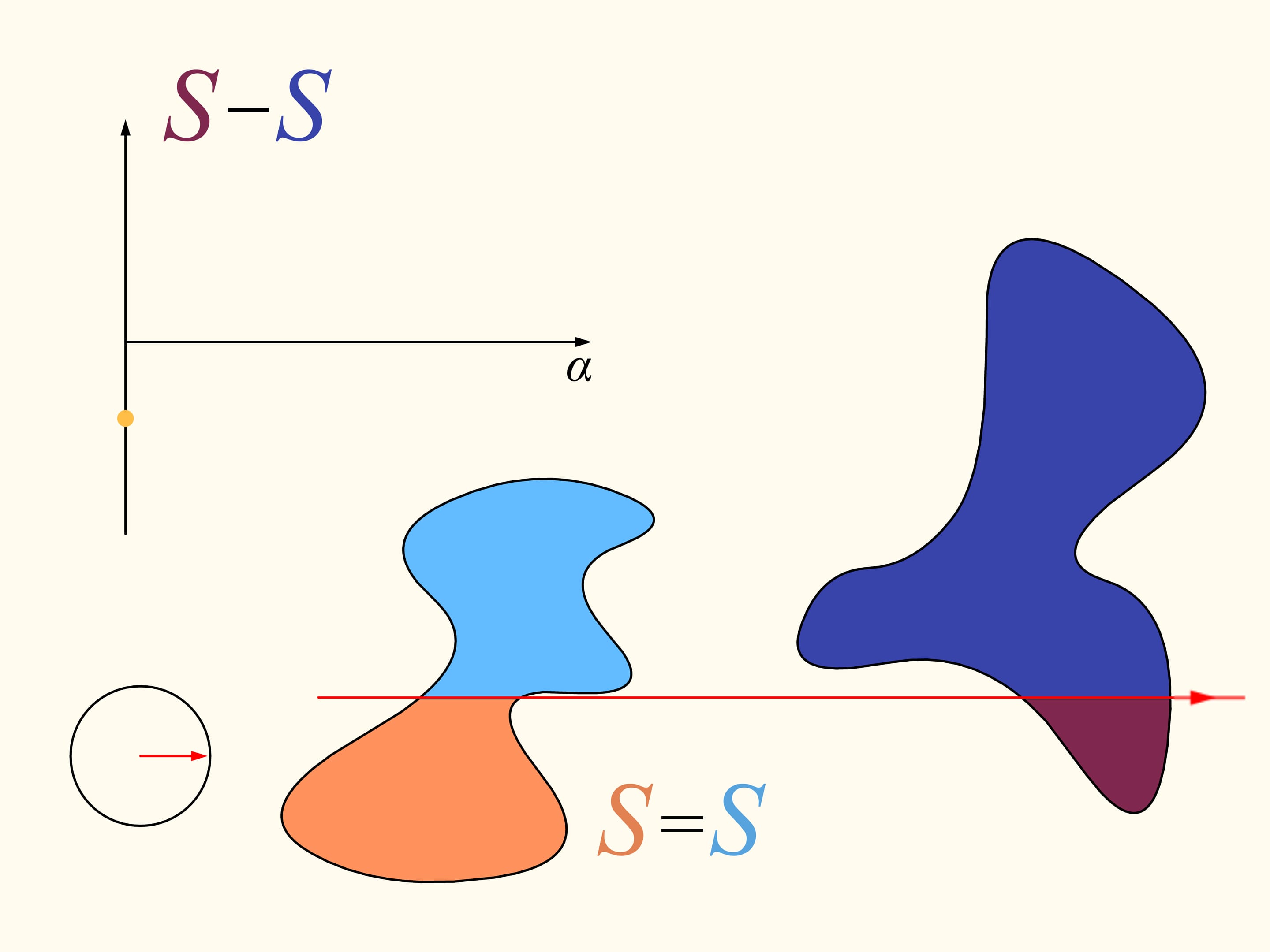
Pour démontrer que telle droite existe, considérons d’abord une seule des régions données. Choisissons une direction arbitraire. Y a–t–il une droite avec cette orientation qui divise la région en deux parties d’aires égales? Nous allons montrer que cette droite existe, n’importe quelle direction étant choisie. Prenons une ligne droite avec la direction choisie de telle façon que la région résulte être entièrement à sa droite. Nous allons construire deux graphes représentant les aires des surfaces de la région qui sont situés à droite et à gauche de la ligne, en fonction de la distance de cette ligne de sa position initiale. Au début, toute la région est située à la droite de la ligne, ce qui signifie que l’élément de l’histogramme à gauche est nulle et celui à droite représente l’aire de toute la région. Commençons à déplacer la ligne vers droite de sorte qu’elle soit toujours parallèle à sa position initiale. Pendant ce déplacement l’aire de la région qui se trouve à droite de la ligne va diminuer avec continuité, tandis que l’aire à sa gauche va augmenter avec continuité. A’ la fin toute la région sera à gauche de la ligne. La partie gauche de l’histogramme (en bleu) représentera l’aire de la région entière, et la partie à droite sera zéro.
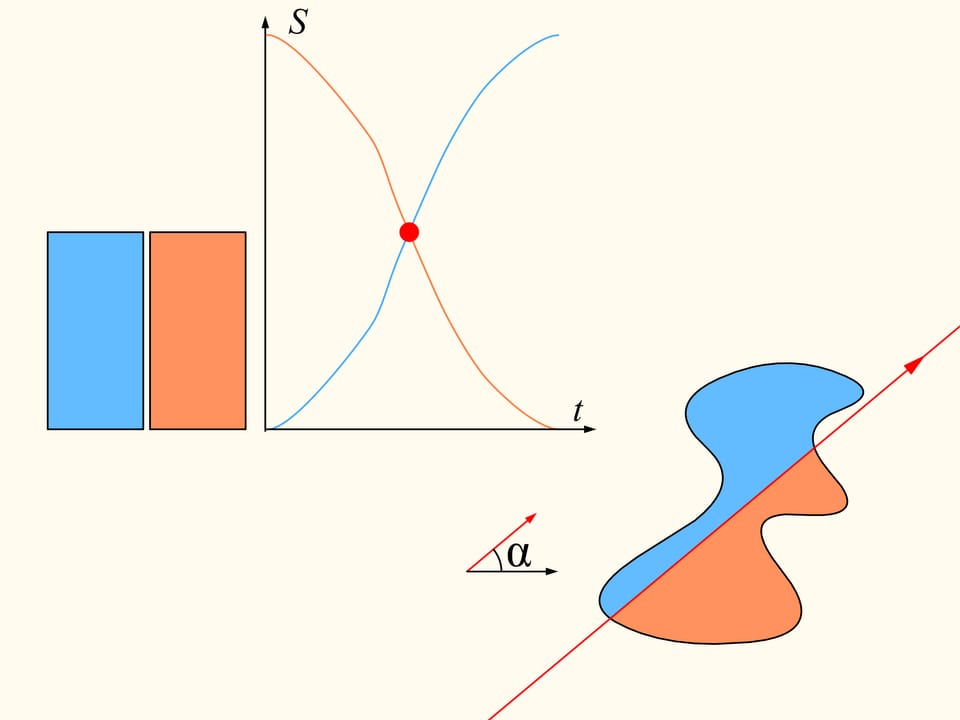
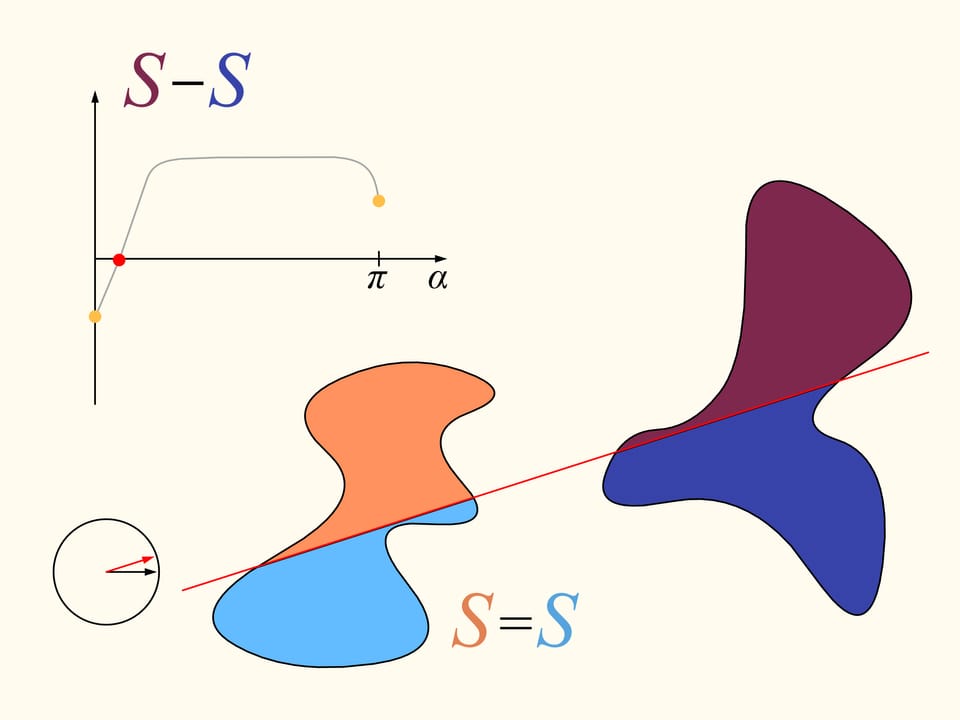
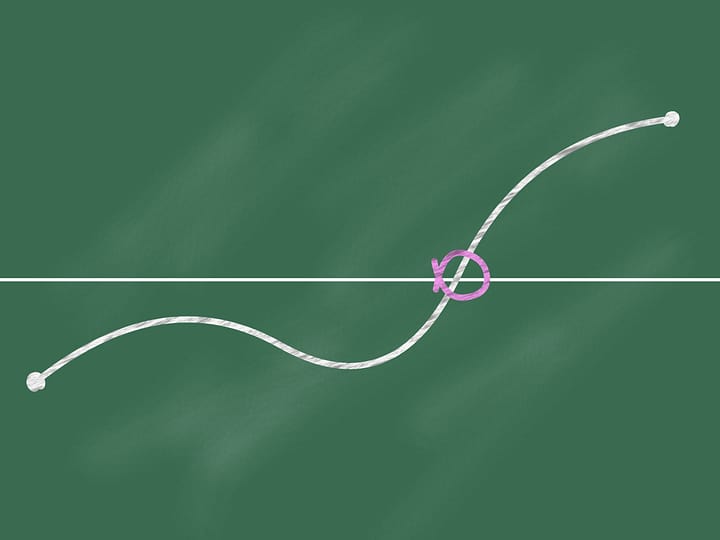
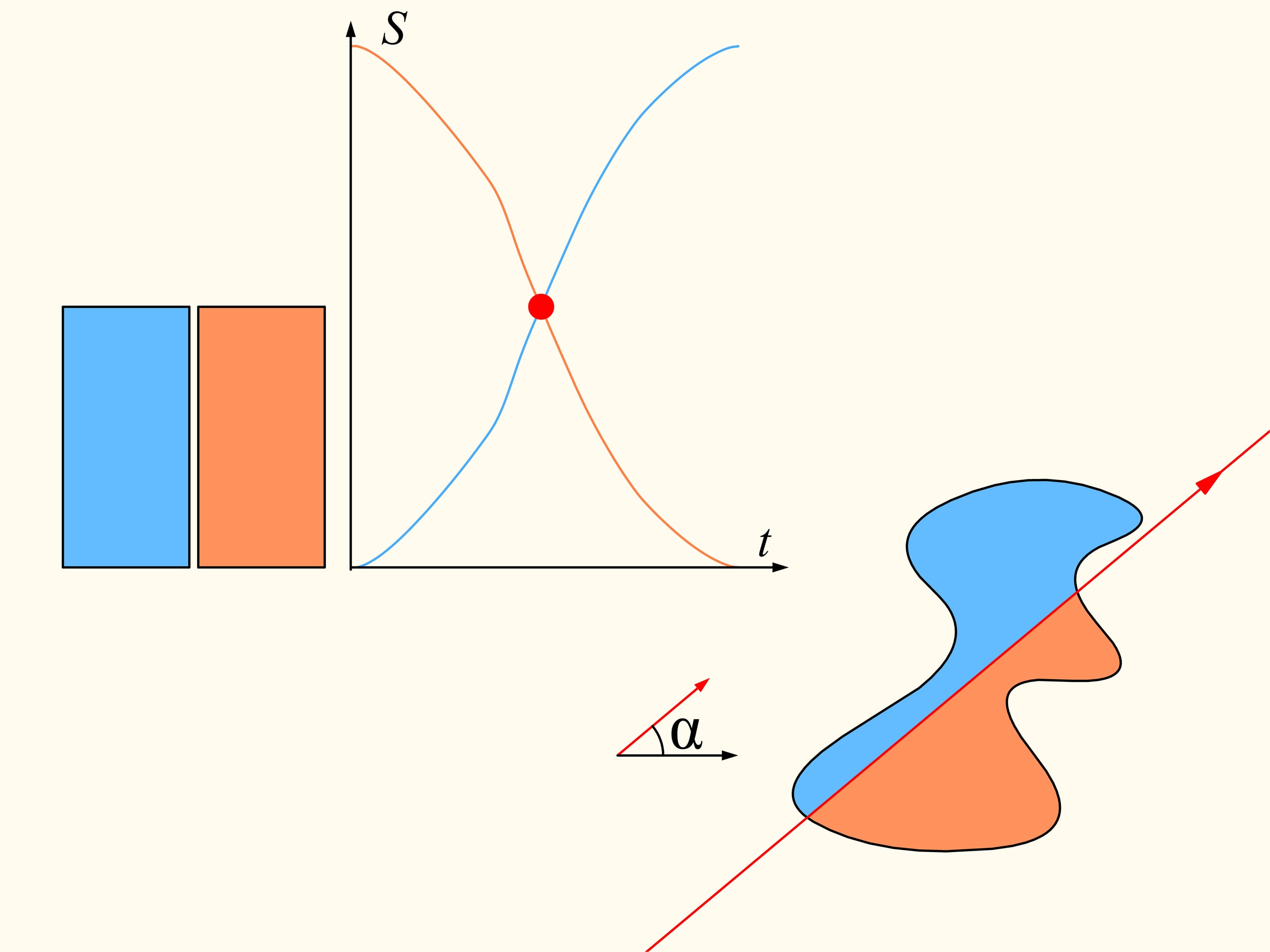
Si l’on regarde les graphes représentant les aires à gauche et à droite de la ligne en fonction de la distance de la ligne de sa position initiale, en raison précisément de leur continuité, il existe quelque part un point d’intersection. Ce point nous dira exactement la position de la ligne qui sépare la région en deux parties de la même aire.
Puisque la direction de la ligne a été choisi arbitrairement, une ligne qui divise la région en deux parties égales existe dans n’importe quelle direction.
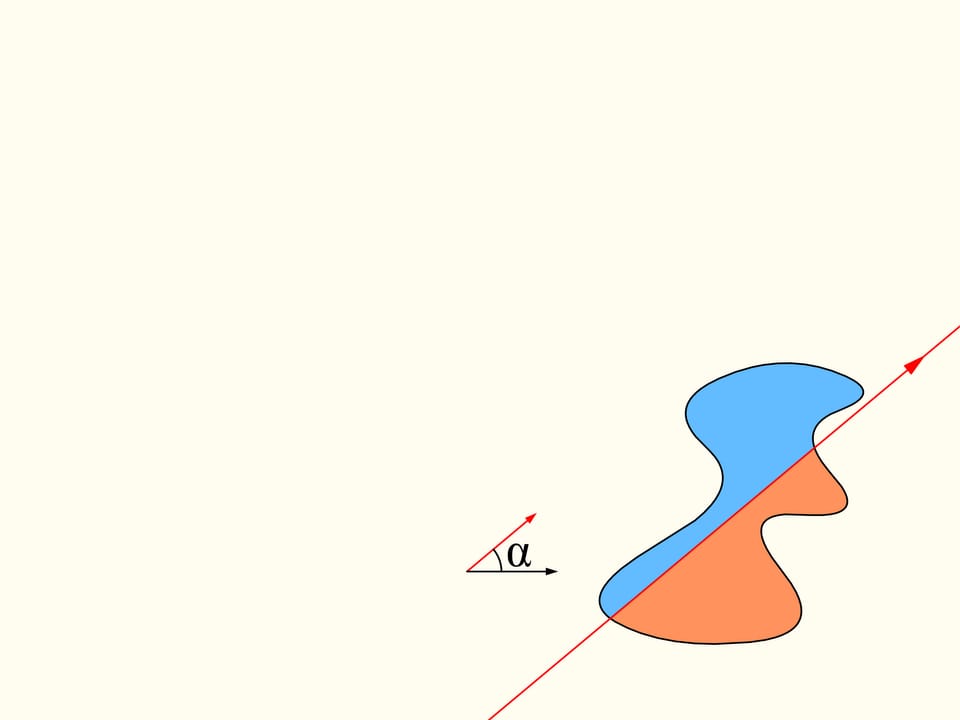
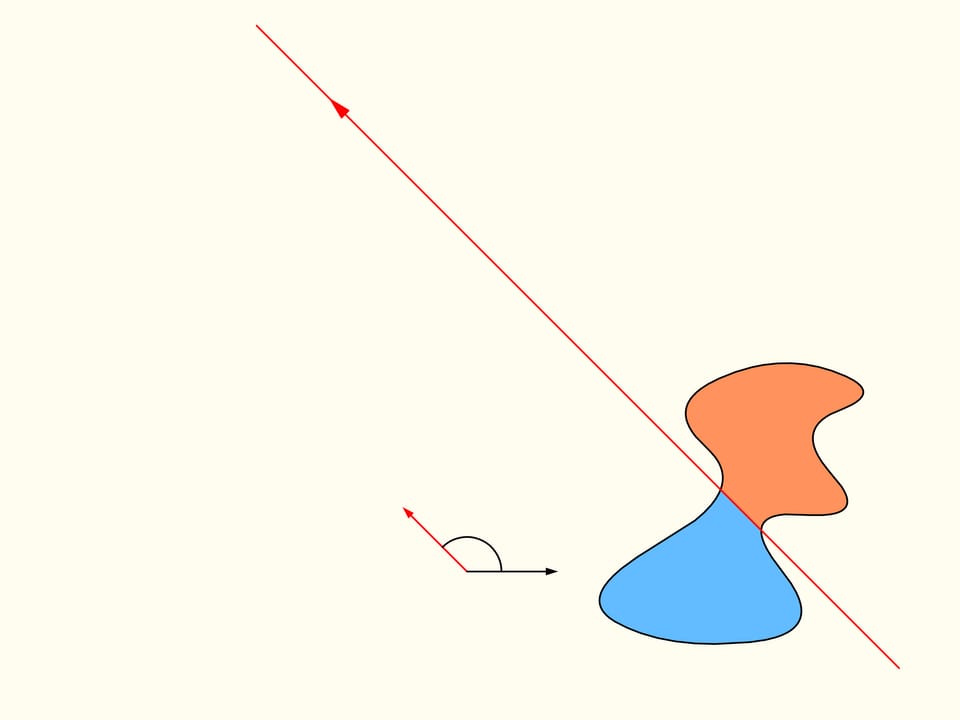
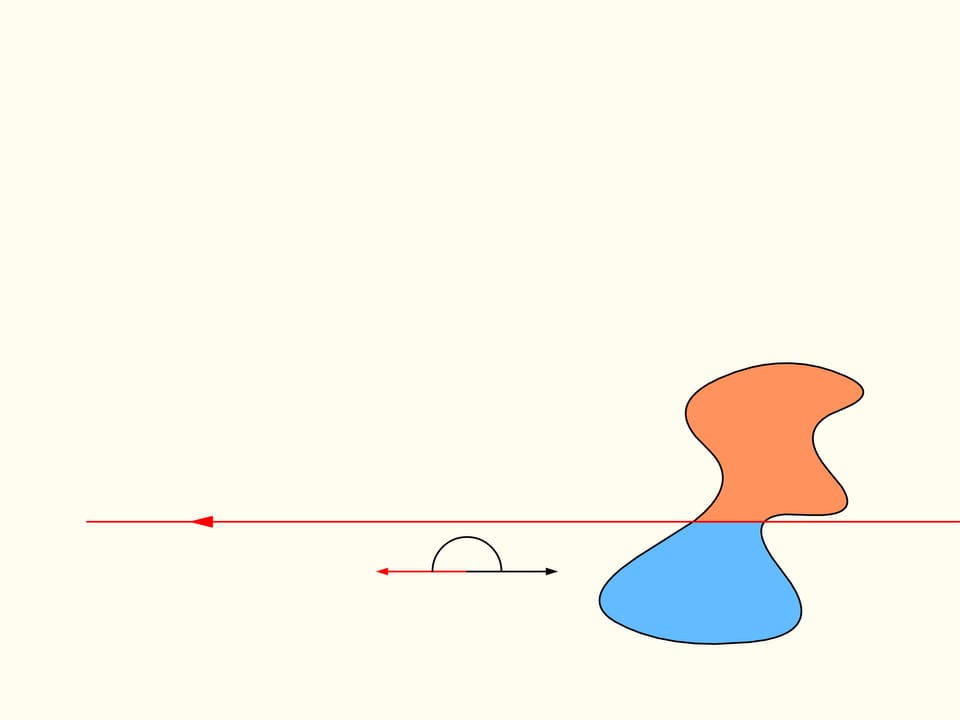
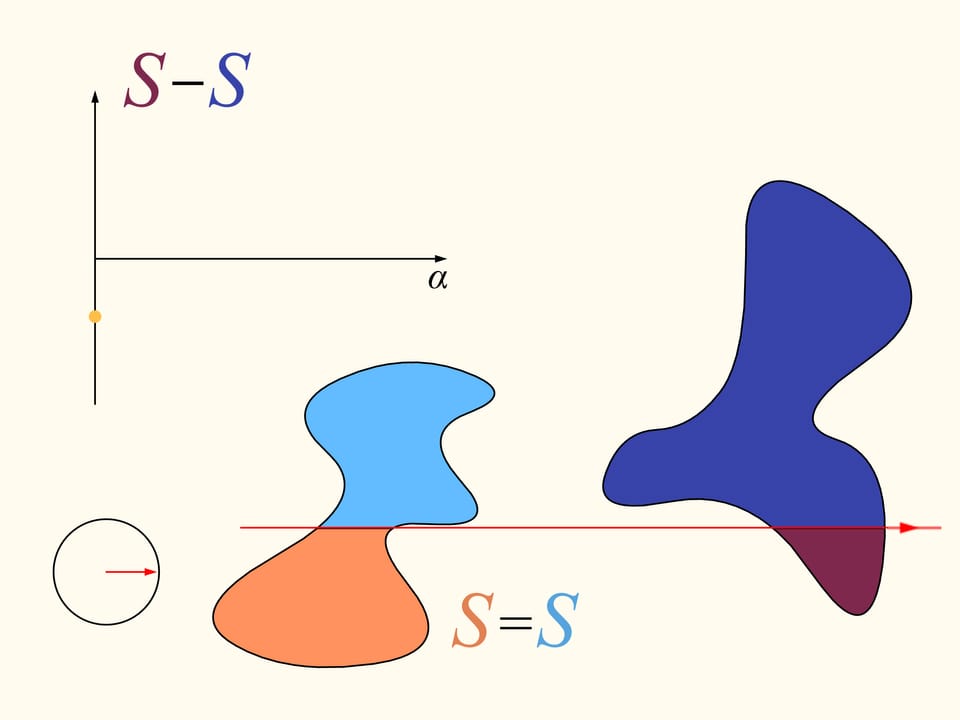
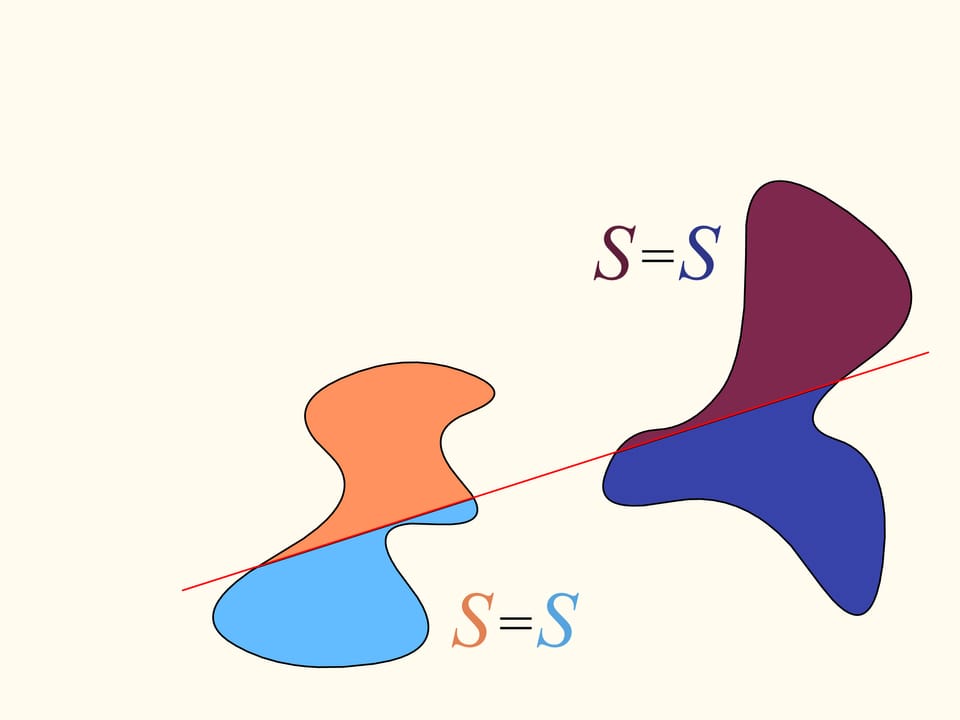
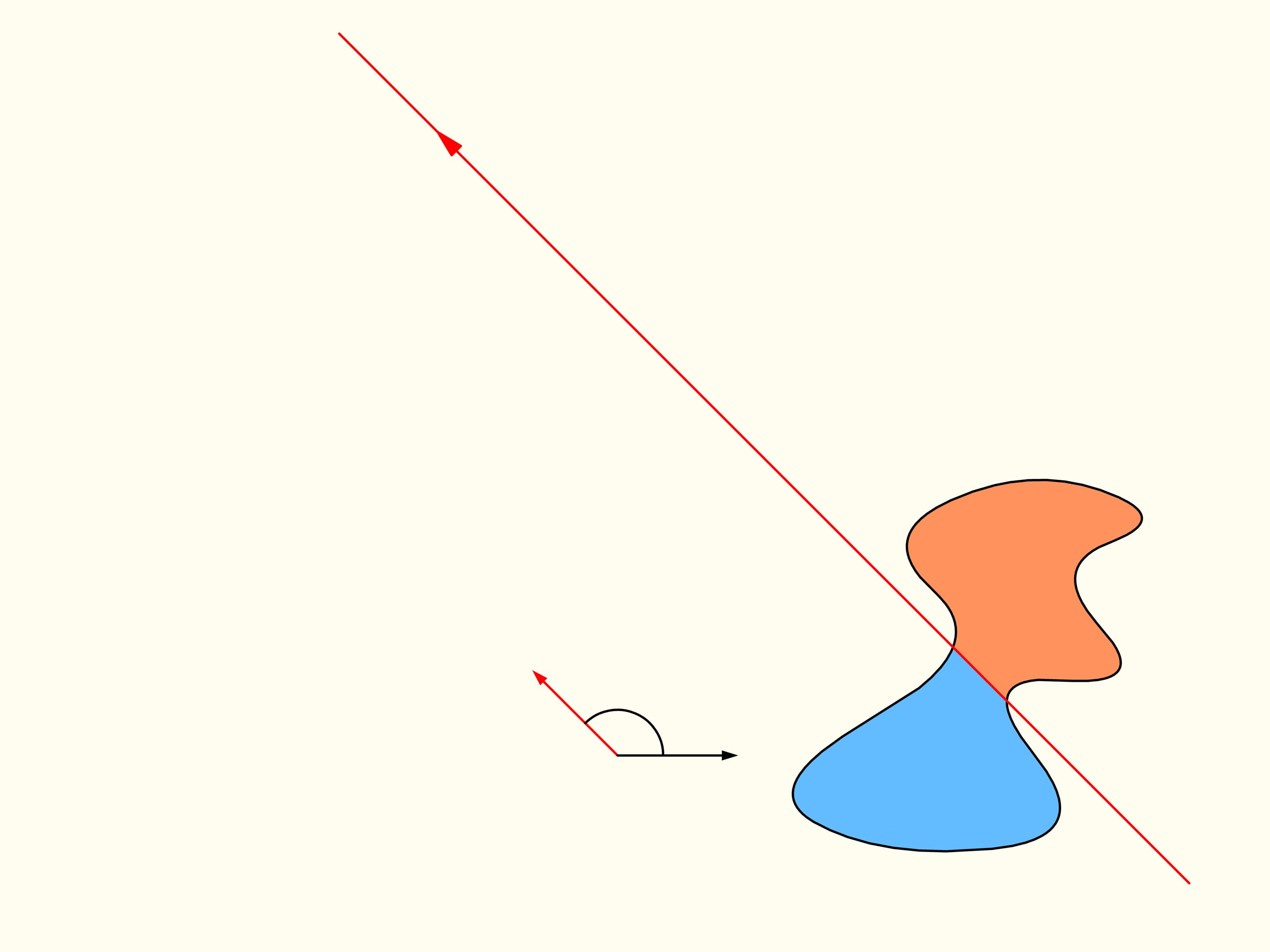
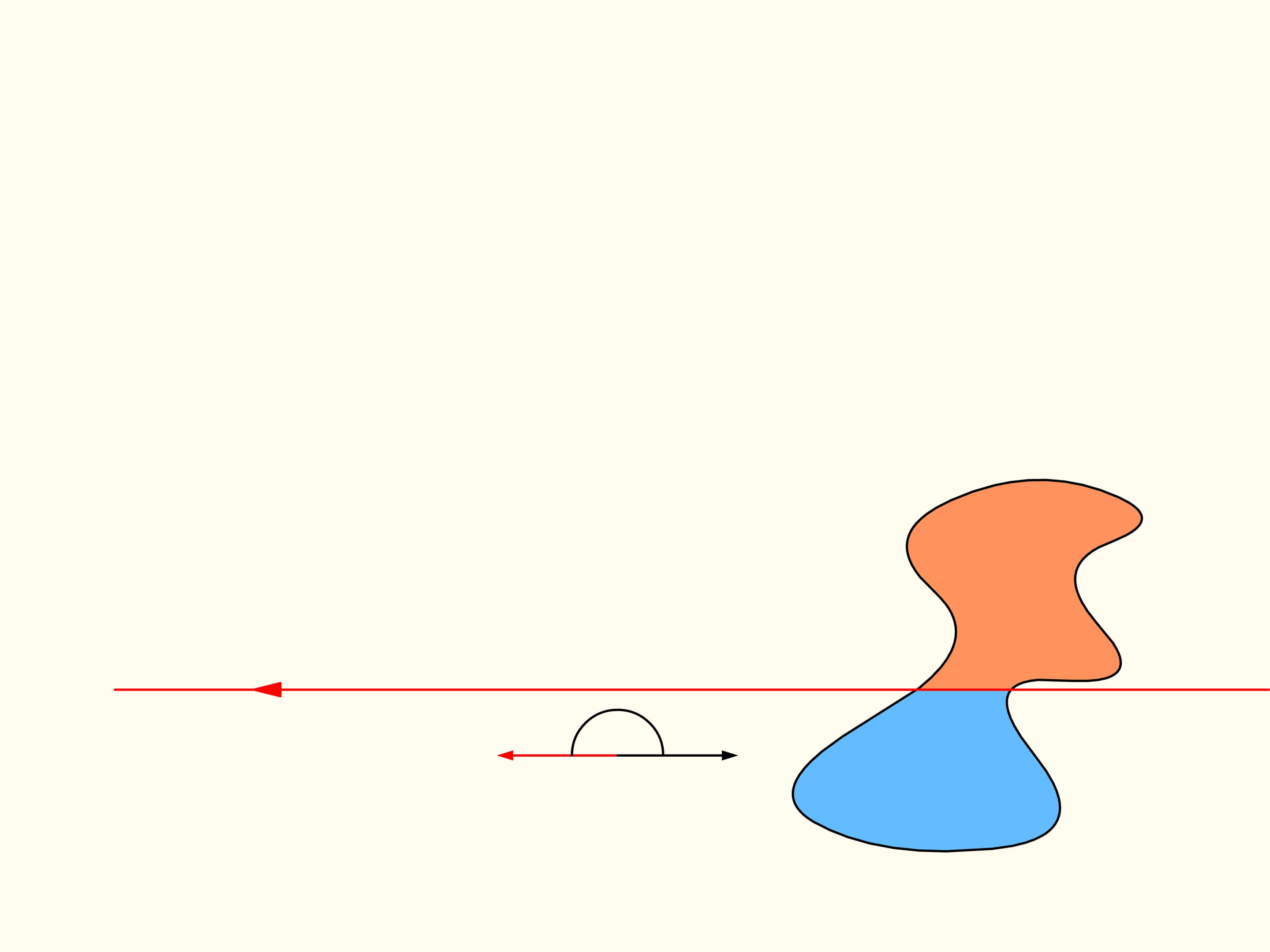
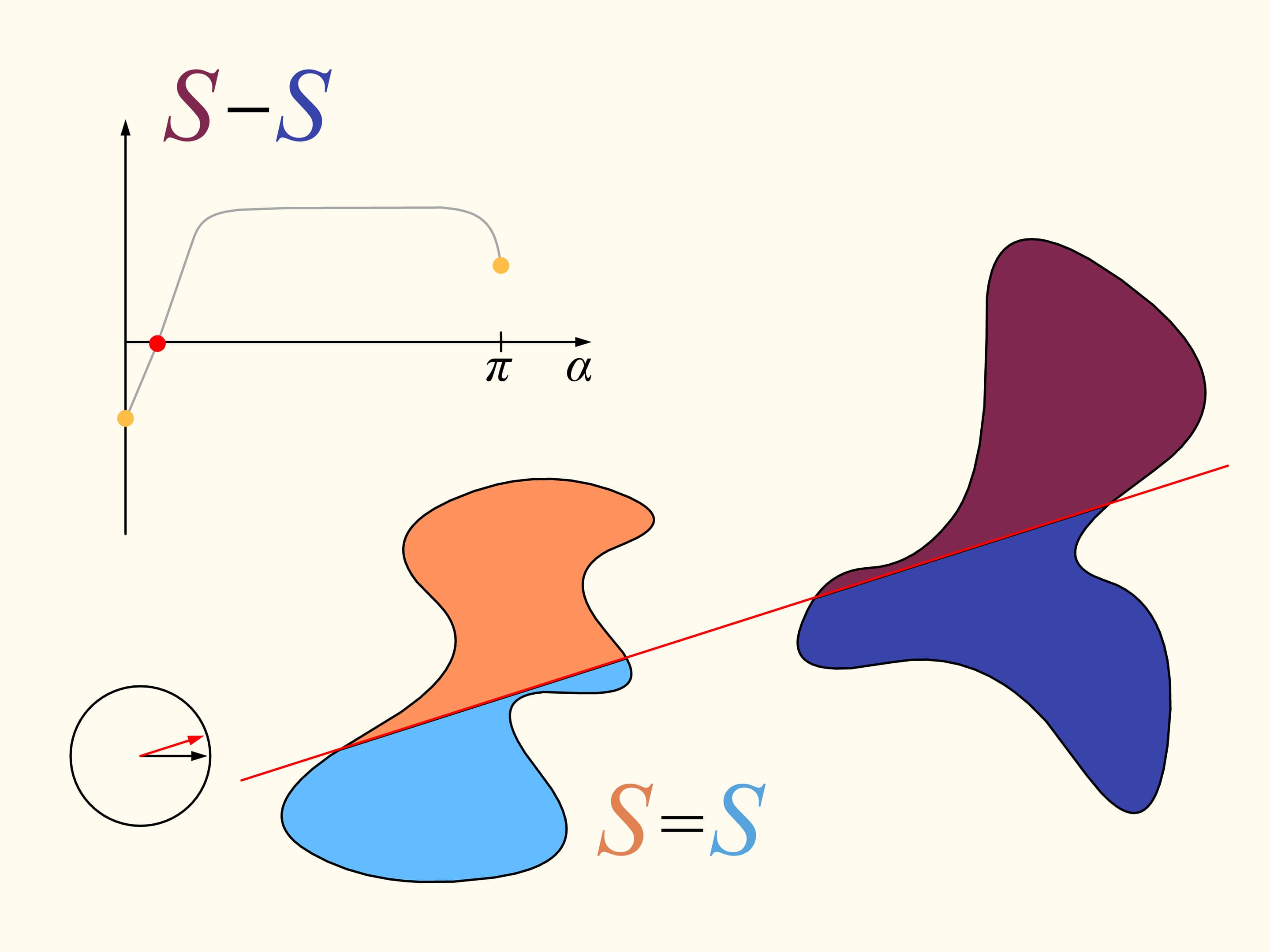
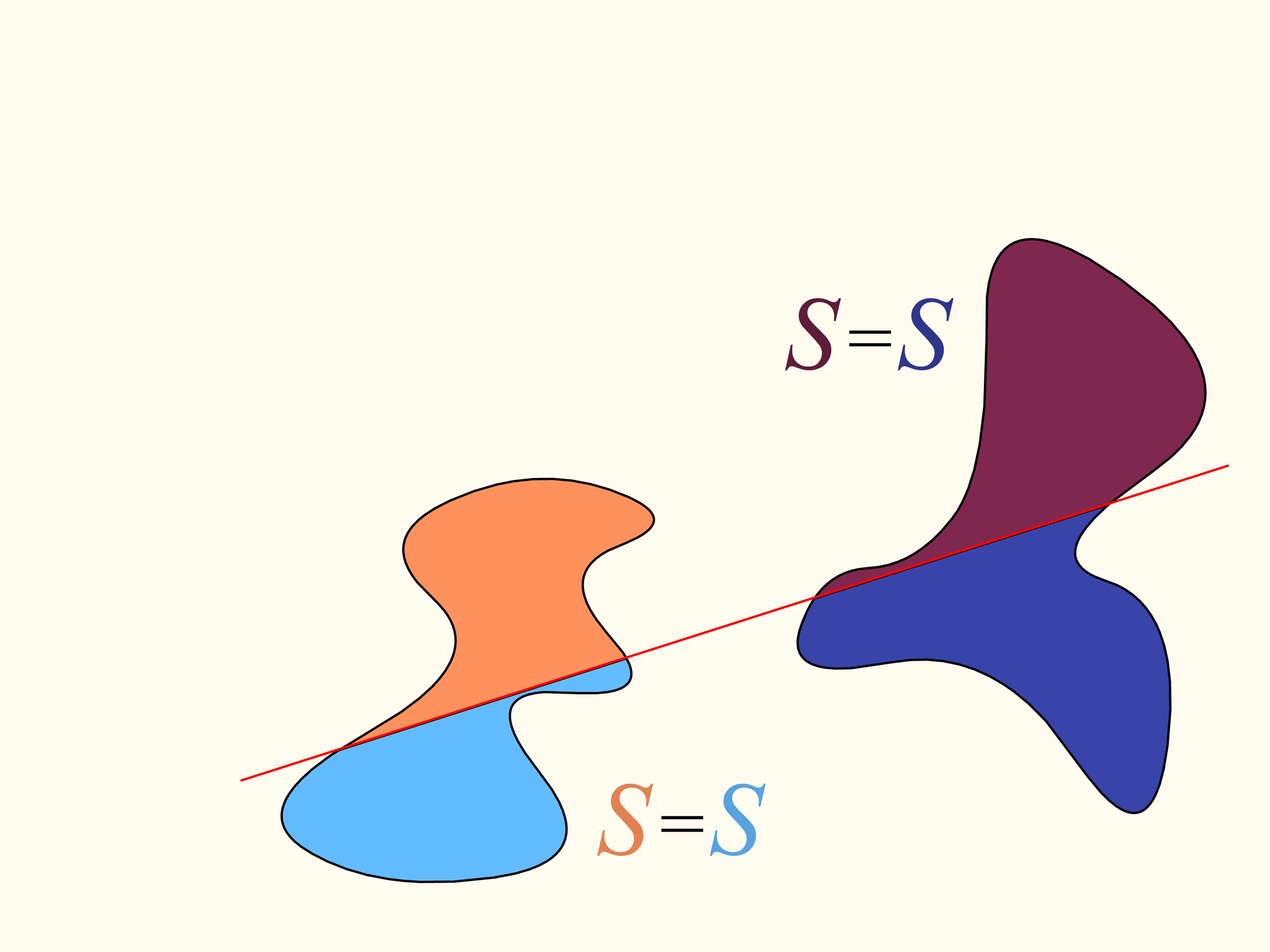
Revenons maintenant au cas de deux régions. Nous considérerons seulement les lignes droites qui découpent la première région (à gauche) en parties égales, et au debout choisissons la droite horizontale orientée vers la droite. Elle coupera la deuxième région (à droite) de quelque façon. Changeons la direction de cette ligne, en restant dans l’ensemble des droites qui divisent la première région en deux parties égales. Dessinons le graphe de la différence entre les aires de la deuxième région qui se trouvent à droite et à gauche de cette ligne, en fonction de l’angle entre cette ligne et sa direction initiale, c’est–à–dire l’horizontale. Au debout cette différence est négative. En changeant la direction avec continuité la droite en fin se trouvera de nouveau dans sa position initiale, mais retournée, ainsi que les aires è droite et à gauche sont échangées entre eux. Dans cet instant la valeur de leur différence est positive. Puisque la différence varie avec continuité, son graphe qui va d’une valeur négative à une valeur positive doit croiser la ligne de la valeur nulle. L’angle correspondant à cette valeur identifie la droite qui divise exactement en deux la deuxième région. Nous avons ainsi trouvé la droite voulue, qui divise les deus régions en deux parties d’aires égales.
Voici comment on utilise le théorème de Bolzano–Cauchy. Malheureusement, la façon de trouver cette ligne étant données des régions de formes arbitraires, arbitrairement disposés l’une par rapport à l’autre, nous ne la pouvons pas connaître, sans l’aide d’autres idées et connaissances. Mais elle existe, pour toute paire de régions! Les théorèmes de ce type sont appelés «théorèmes d’existence».
Passons maintenant au cas de trois dimensions. Au lieu de deux régions dans le plan à deux dimensions, nous considérons trois objets arbitraires, arbitrairement disposées rapport l’un à l’autre dans l’espace. Au lieu des aires, nous allons considérer les volumes, et au lieu d’une droite, un plan. Il arrive que dans ce cas par un argument pareil à celui utilisé dans le plan, nous pouvons démontrer un théorème d’existence. Pour tout choix arbitraire de trois objets il existe un plan qui divise chacun objet en deux parties de volumes égaux.
Pour que la vie aie plus de saveur, considérons un sandwich fait d’une tranche de pain, une de fromage et une de jambon. Il s’agit de trois objets disposés d’une certaine façon l’un par rapport à l’autre. Essayez de démontrer qu’il y a un plan qui coupe le jambon en deux parties égales et coupes simultanément soit le fromage soit le pain en parties égales. En utilisant des arguments supplémentaires, ce plan a été trouvé pour le sandwich montré dans le film, où il sera évident que les trois objets ont été divisés en deux parties égales!