Solide invisibles ⁠

Herbert Wells est allé trois fois en Russie. Pendant sa deuxième visite — à ce temps là il y avait déjà l’Union Sovié­tique — il rencontra Yakov Perelman Isido­ro­vich, qui soumit à l’atten­tion de l’auteur de “L’homme invi­sible” le fait suivant: si un homme est complè­te­ment invi­sible, aussi les cris­tal­lins de ses yeux sont invi­sibles, et donc ne réfractent la lumière et ne donne pas l’image sur la rétine. Pour cet homme, tout est invi­sible!

Mais y a–y–il des corps invi­sibles, quoique inanimés? En 2009, les mathé­ma­ti­ciens ont démontré qu’il existe des êtres invi­sibles inanimés!

Mais commençons par le XVIIe siècle. Dans «Les prin­cipes mathé­ma­tiques de la philo­so­phie natu­relle» («Philo­so­phiae Natu­ralis Prin­cipia Mathe­ma­tica») Isaac Newton a étudié le problème de la chute (ou mouve­ment) de corps diffé­rents dans un milieu «raréfié, constitué de parti­cules iden­tiques, arbi­trai­re­ment placé à la même distance les unes des autres» qui rebon­dissent élas­tique­ment lorsqu’elles entrent en colli­sion avec le corps. Plus tard, ce problème a été appelé «problème aéro­dy­na­mique de Newton».

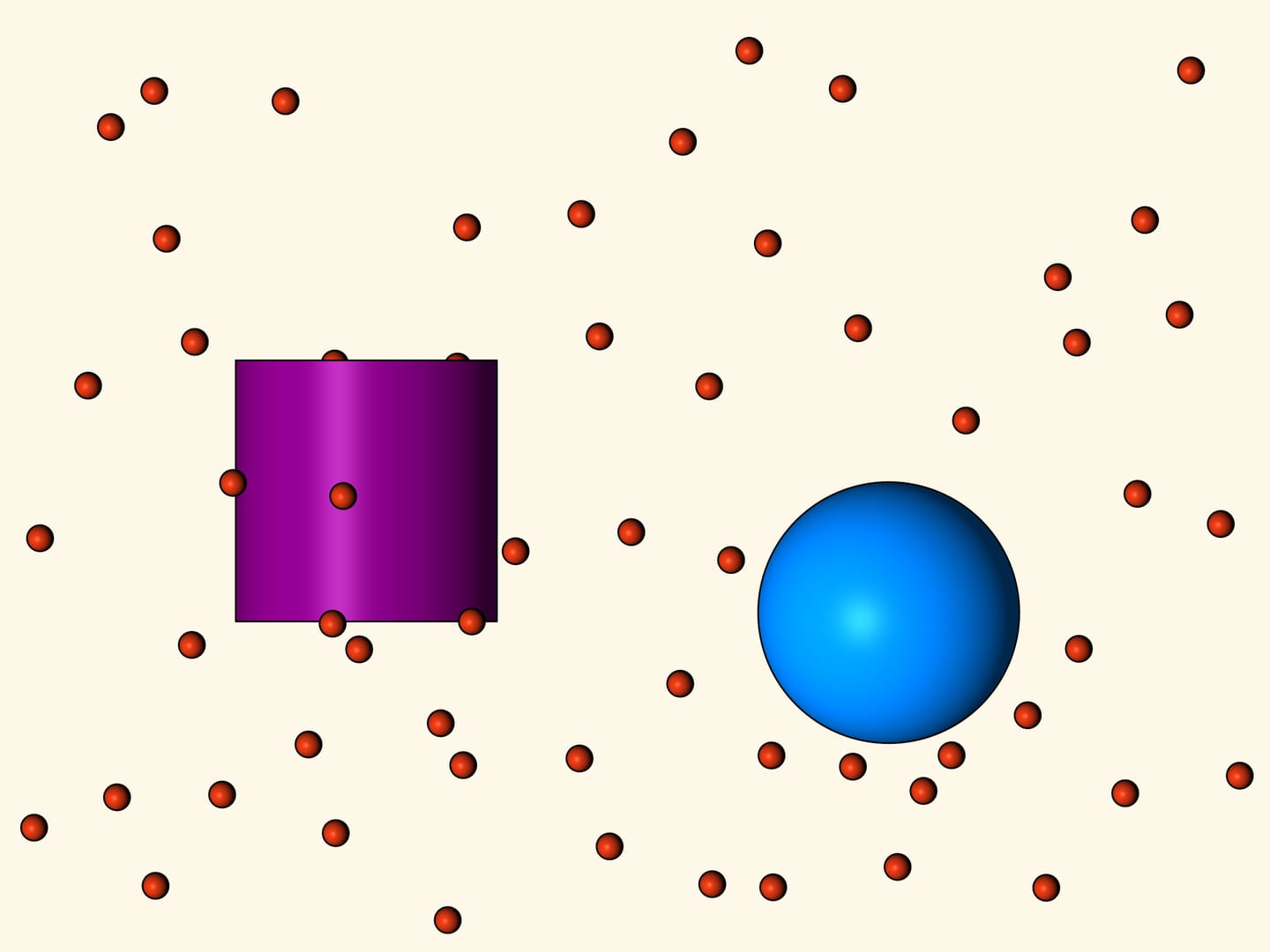
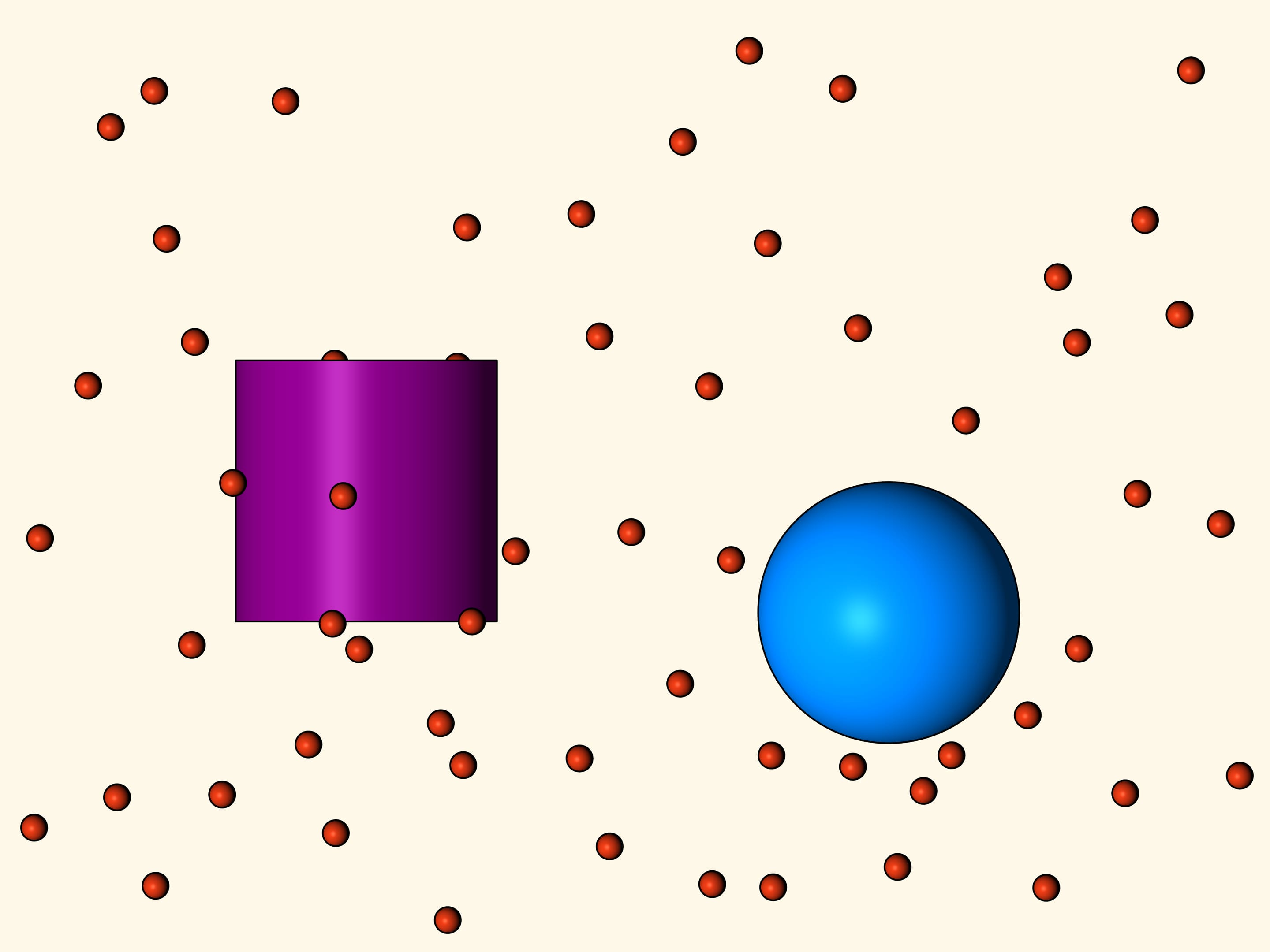
Les deux premiers corps consi­dérés sont une sphère et un cylindre, avec le même diamètre. Lequel de ces corps rencontre moins de résis­tance? Newton montre par des méthodes géomé­triques que la résis­tance pour la sphère sera deux fois plus faible.

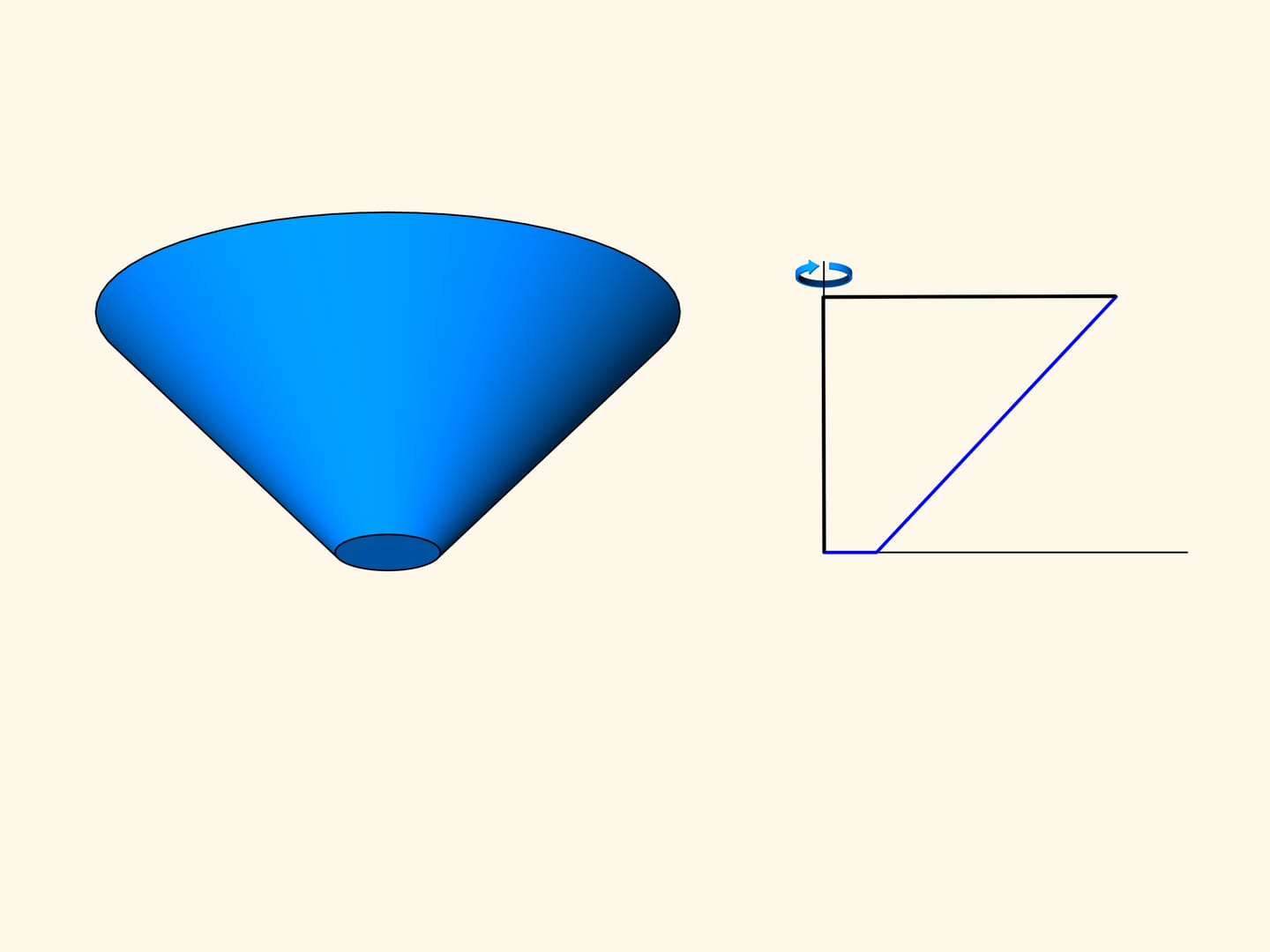
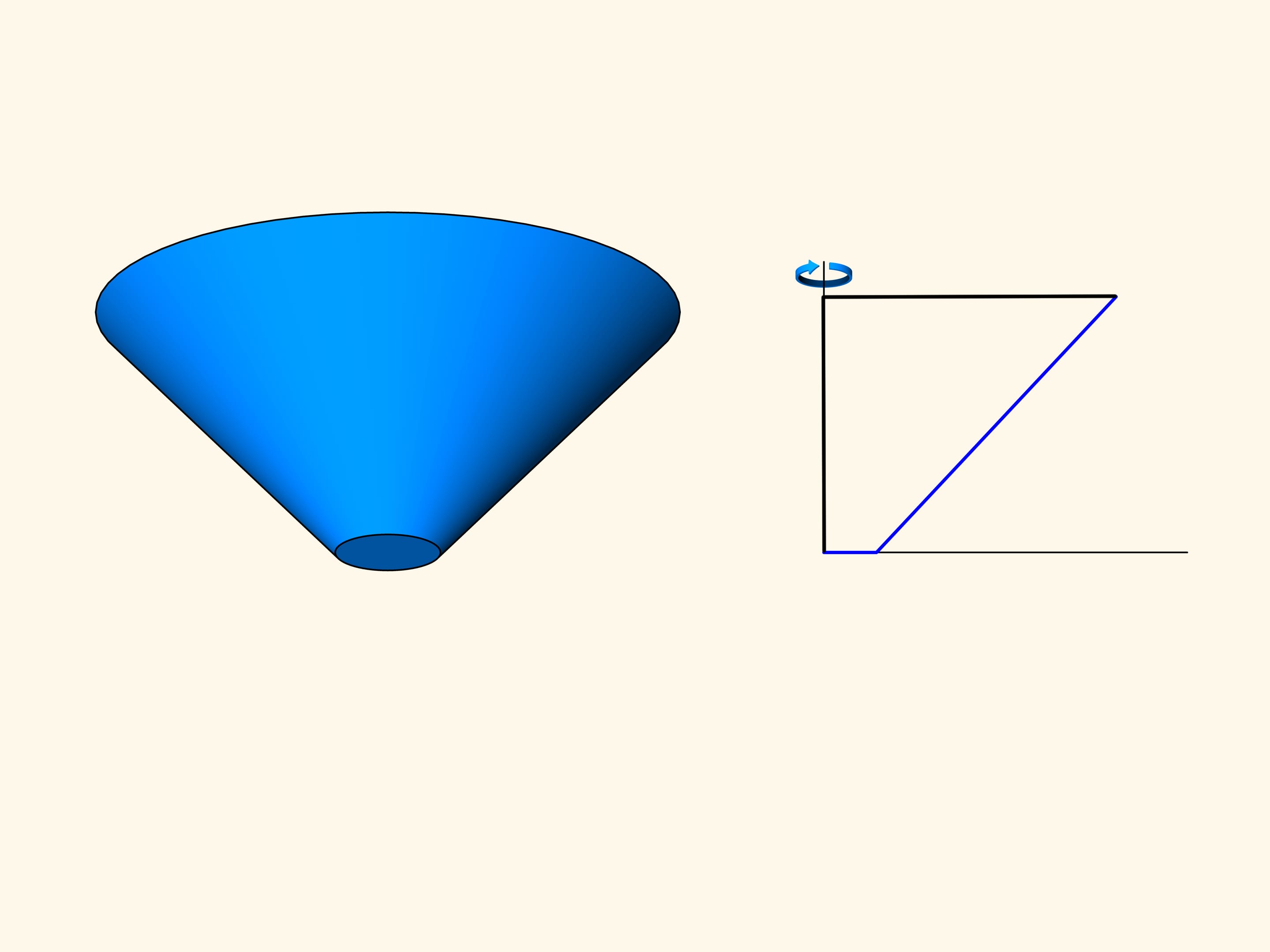
Ensuite Newton commence à étudier les cônes tronqués. Parmi tous les cônes tronqués avec le rayon de la base et la hauteur fixés, trouver celui pour lequel la résis­tance dans un milieu raréfié — pour un mouve­ment le long de l’axe du cône — est minime.

Consi­dé­rons une section du tronc de cône et le problème dans le cas planaire.

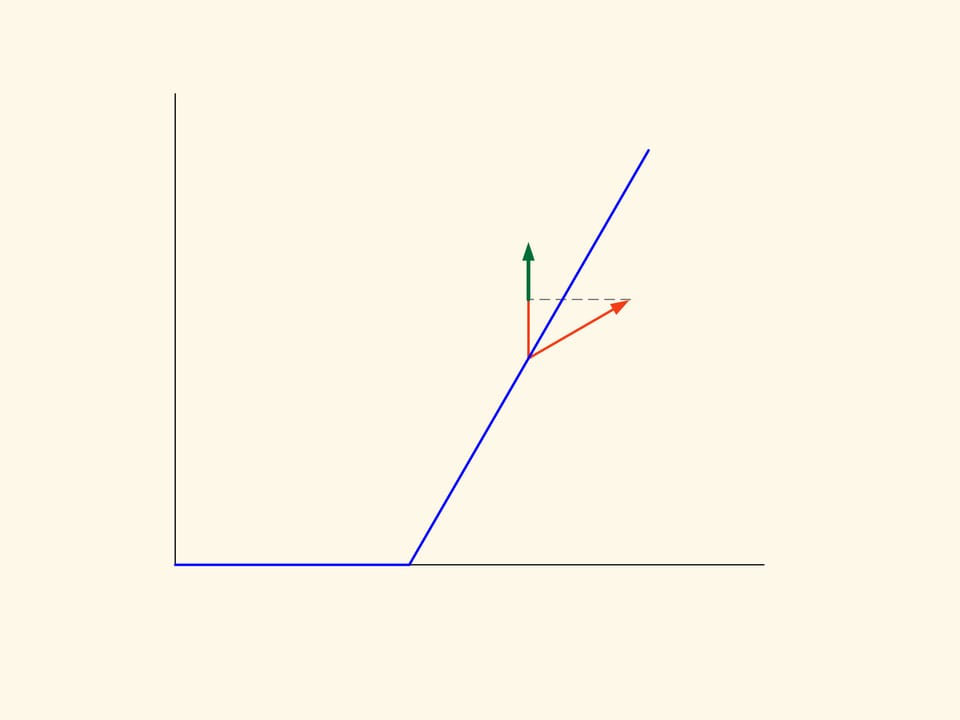
Qu’est ce que c’est la résis­tance? Lorsque le cône tombe, il entre en colli­sion avec les sphères — les parti­cules du milieu raréfié. Une partie des sphères heurte contre la surface infé­rieure du tronc de cône, et une partie avec la surface laté­rale, les autres bougent sans s’arrêter et sans souf­frir de l’effet du corps. Quand une parti­cule entre en colli­sion avec le tronc de cône, modifie sa direc­tion de mouve­ment confor­mé­ment à la loi que «l’angle d’inci­dence est égal à l’angle de réflexion». La résis­tance que la sphère exerce contre la chute du tronc de cône est le chan­ge­ment de la compo­sante verti­cale du vecteur impul­sion de la sphère. Puisque les parti­cules heurtent unifor­mé­ment en moyenne sur la surface du corps, les pous­sées vers gauche et vers droite se compensent mutuel­le­ment et ne doivent pas être consi­dérés.

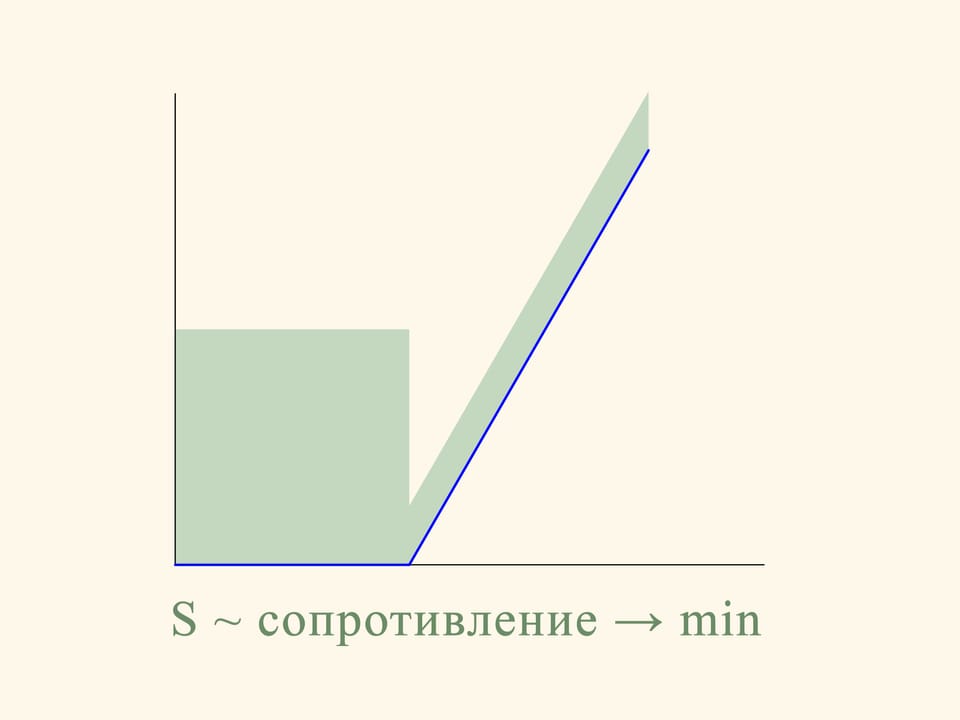
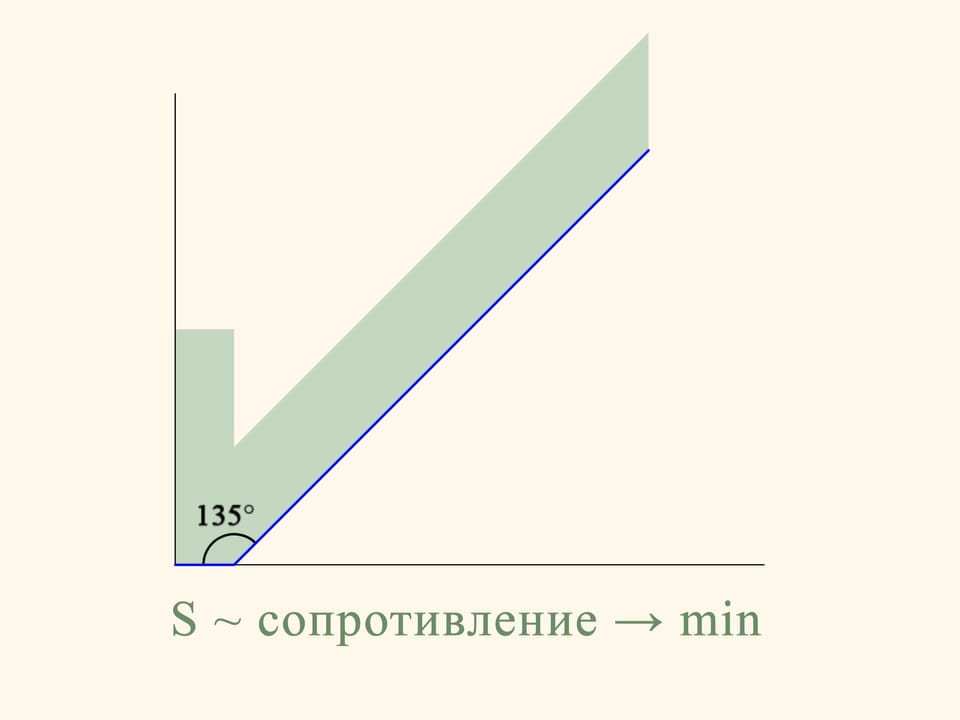
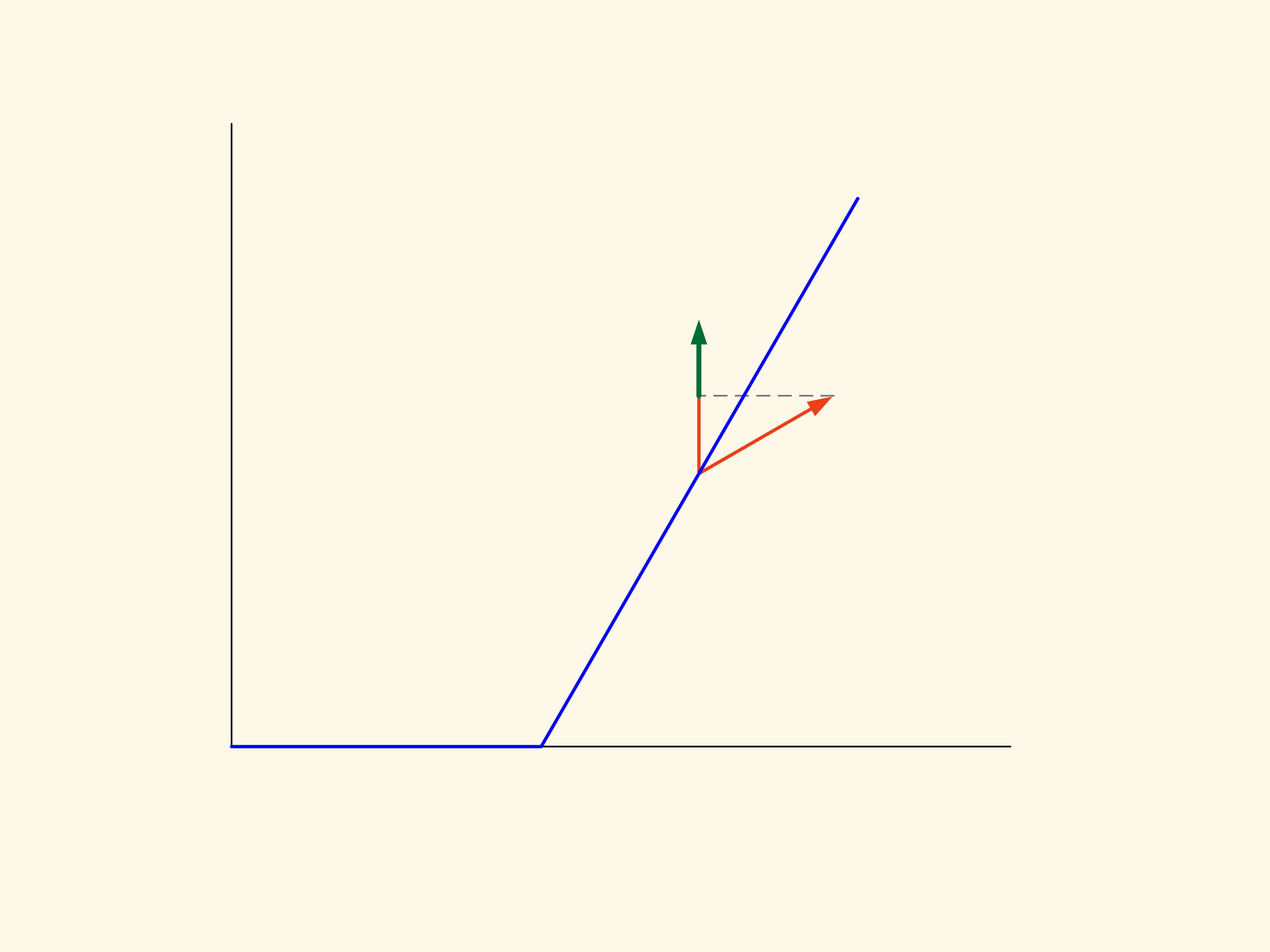
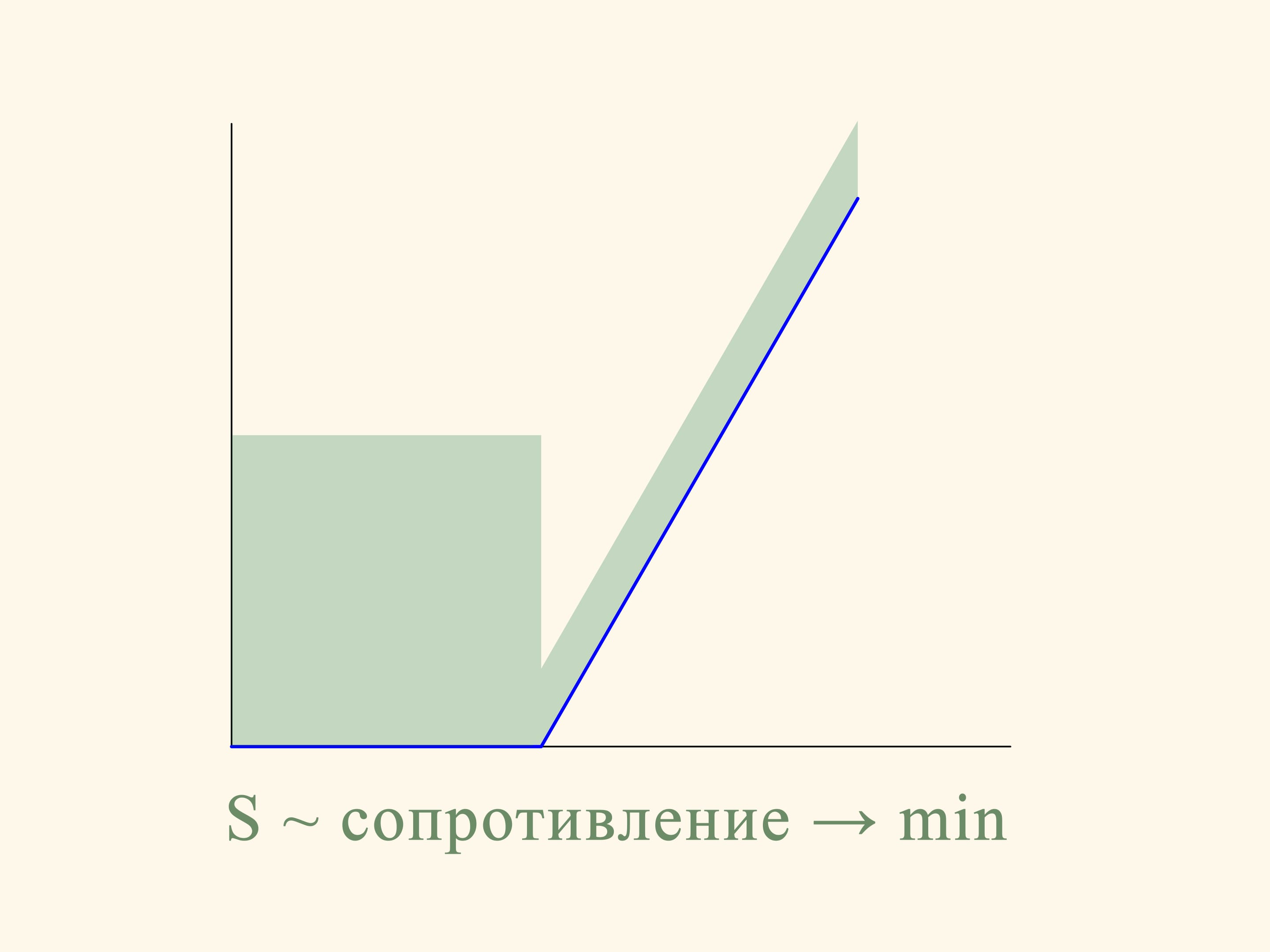
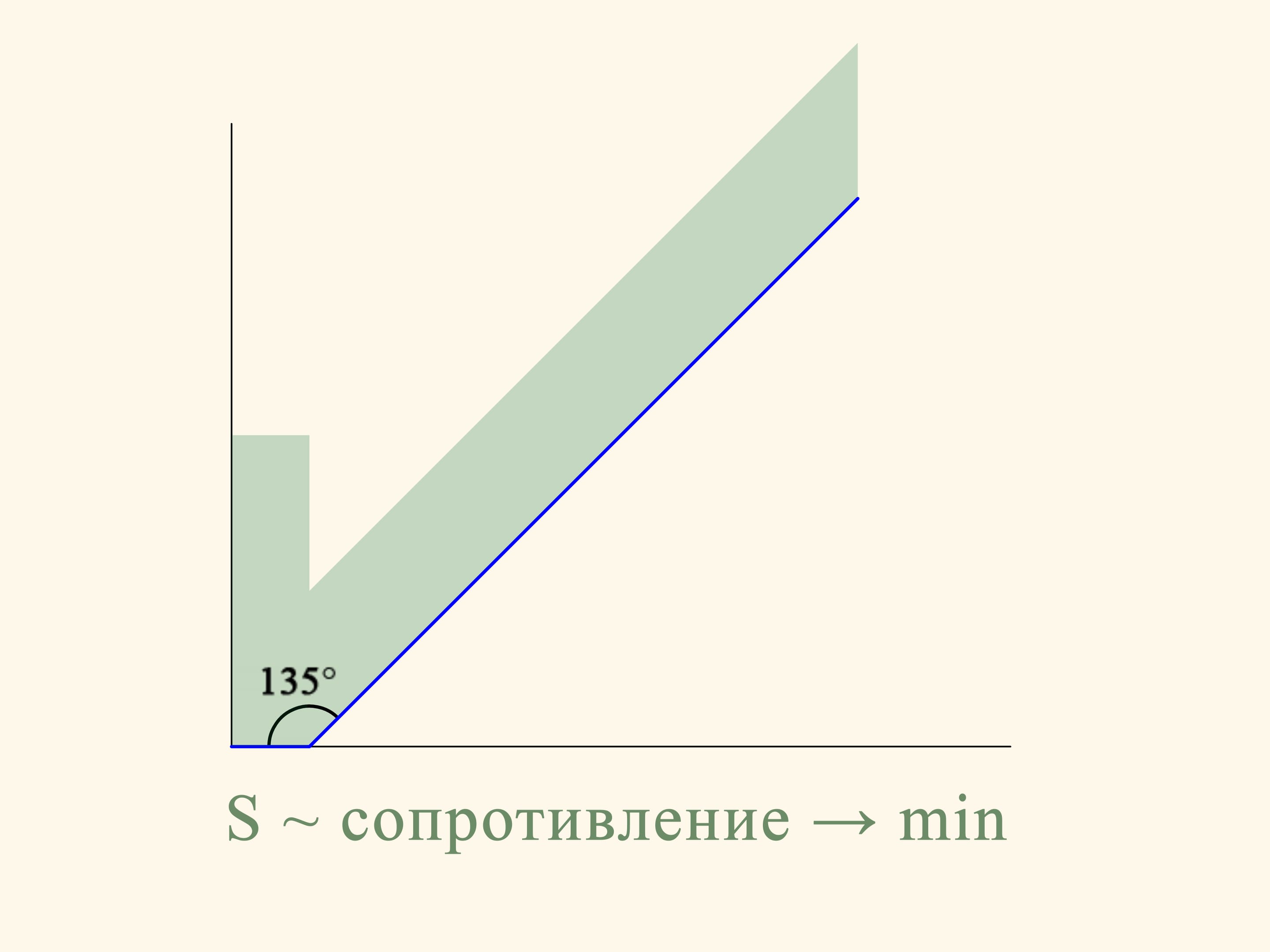
Dans le cas planaire la résis­tance de la section du cône tronqué est propor­tion­nelle à la somme des aires d’un rectangle construit sur la base plus petite du trapèze et d’un paral­lé­lo­gramme, construit sur le côté oblique. Et cette résis­tance doit être mini­misée. Si on fait le calcul, on constate que l’aire de la figure en vert est minime lorsque l’angle entre la base et le côté oblique est égale à 135°. Autre­ment dit, la sphère après la colli­sion avec le côté oblique bougera en direc­tion stric­te­ment hori­zon­tale.

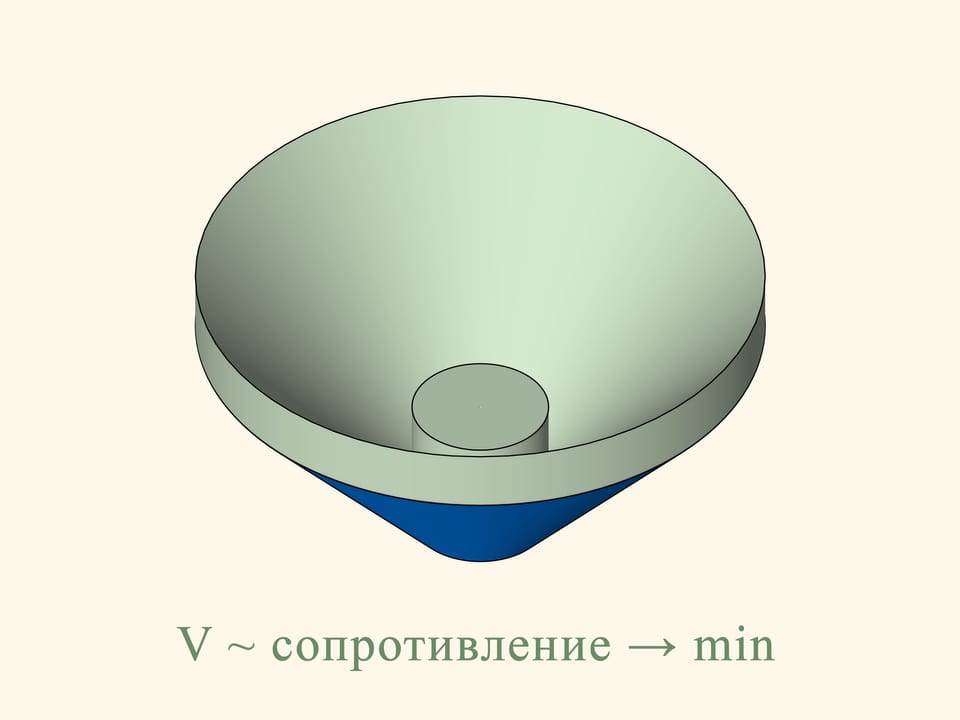
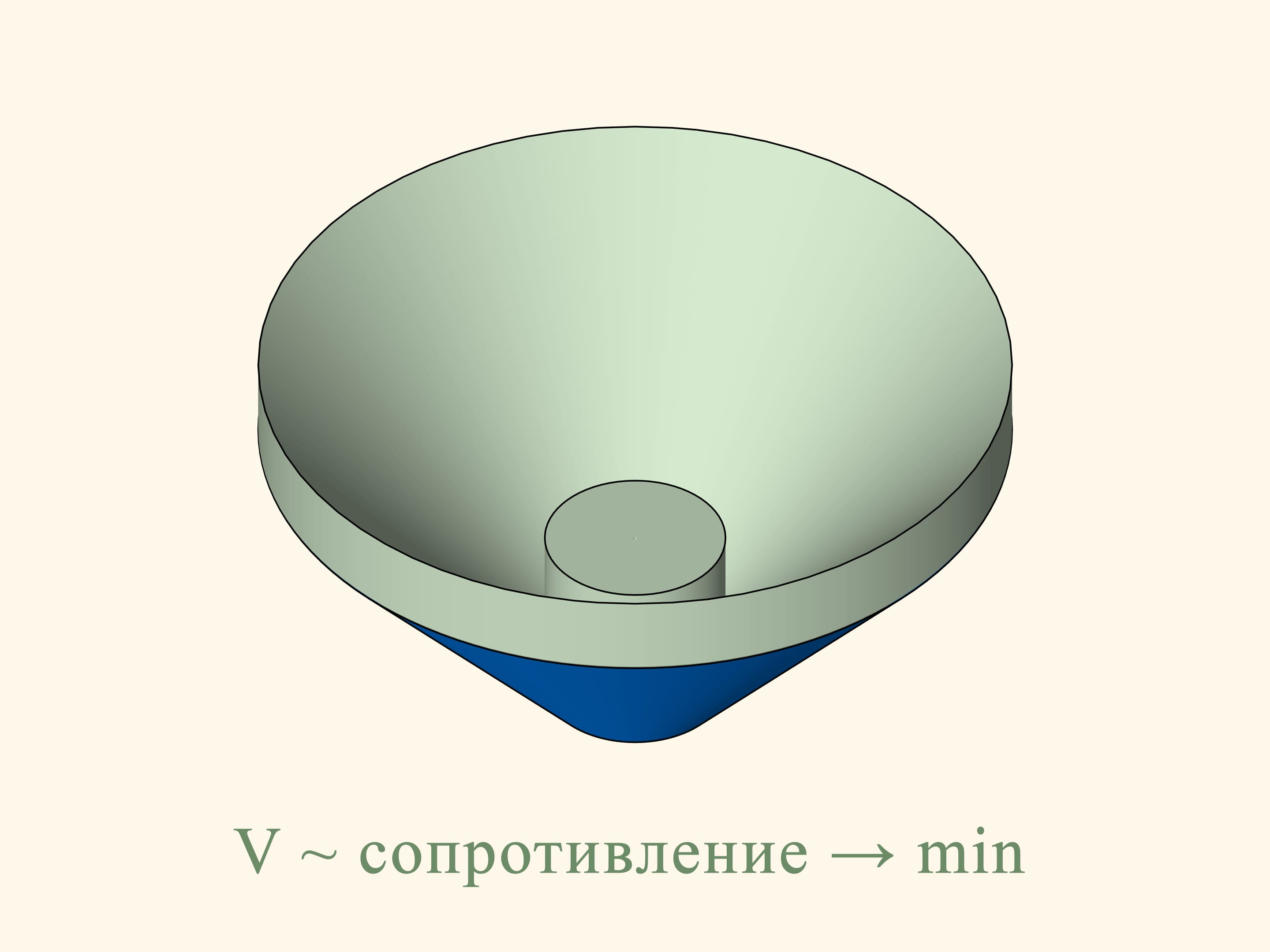
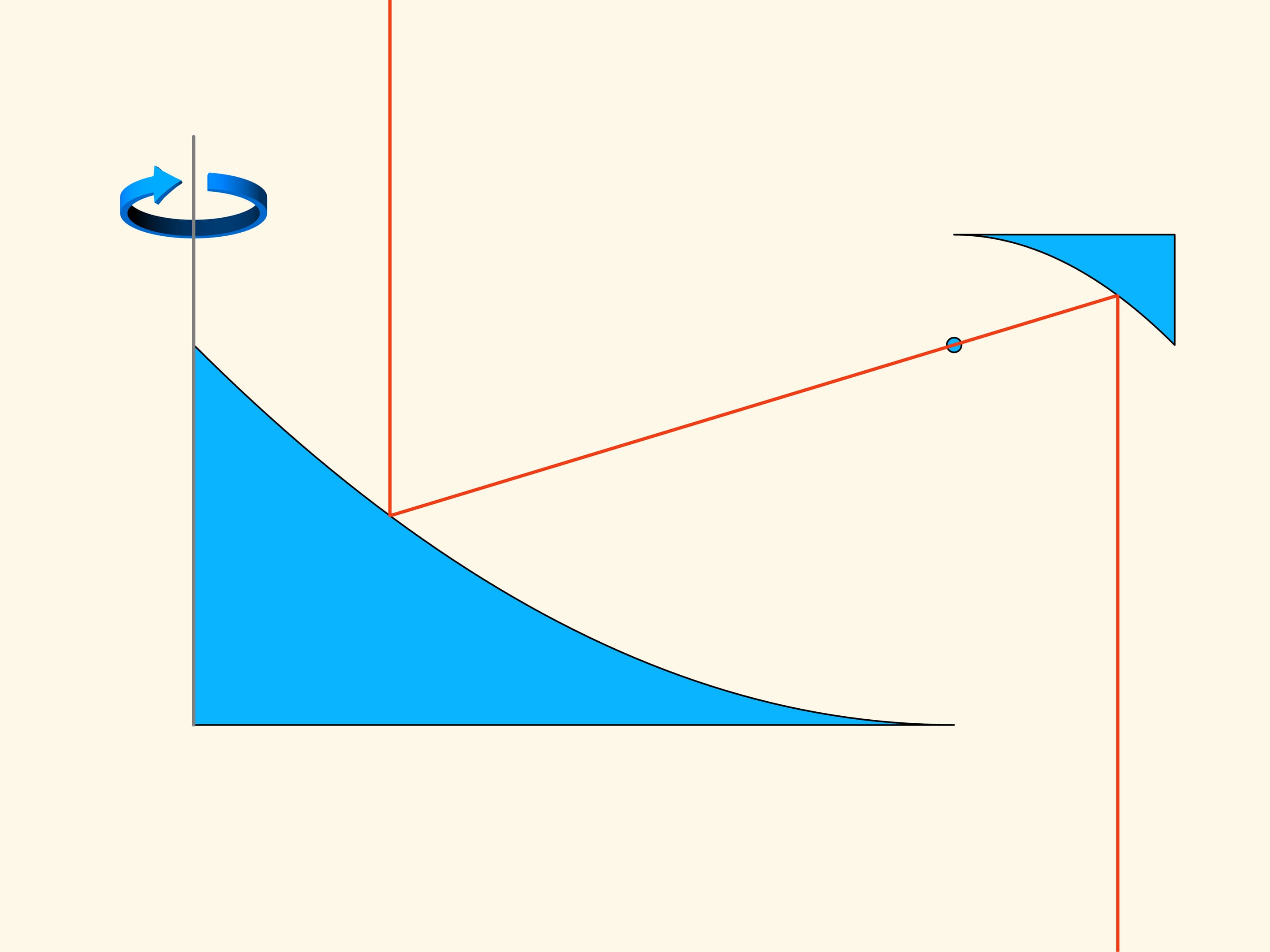
Est–ce qu’il suivra de la solu­tion planaire du problème, que la section du cône tronqué opti­male pour le problème en trois dimen­sions doit satis­faire la même condi­tion? Il s’avère que non. Pour passer d’une section d’un objet à l’objet lui–même, il faut tourner la figure plane autour de l’axe vertical. Les petits segments verti­caux plus éloigné de l’axe, formant l’aire, décri­ront une trajec­toire beau­coup plus longue pendant la rota­tion et ils donne­ront donc une contri­bu­tion plus grande au volume. Par conséquence, on ne peut pas trouver le volume minimum en utili­sant la solu­tion du problème dans le plan.

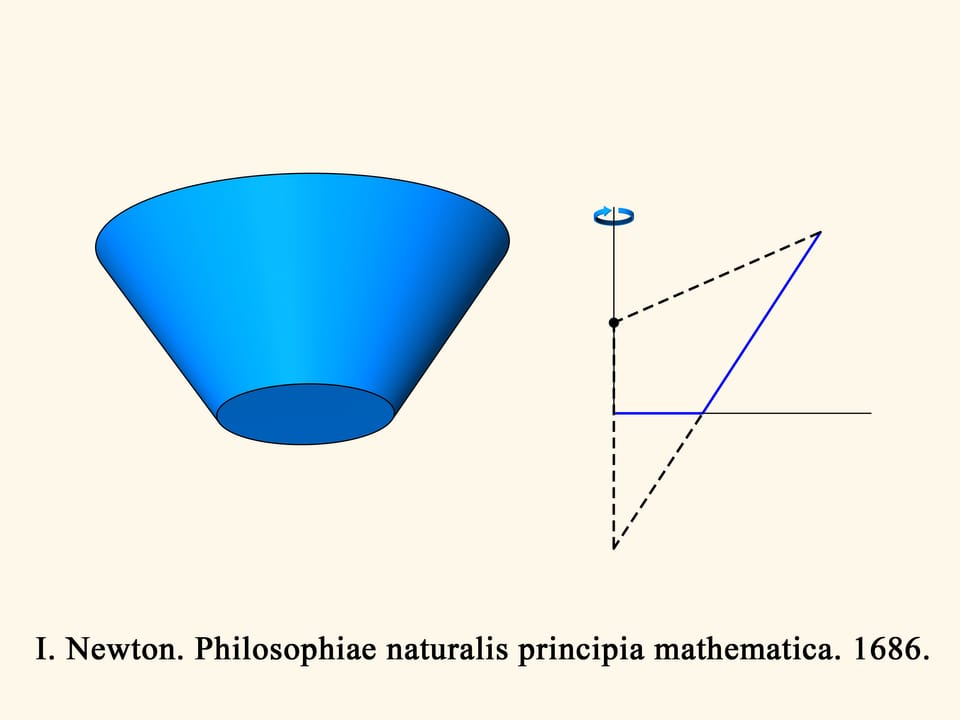
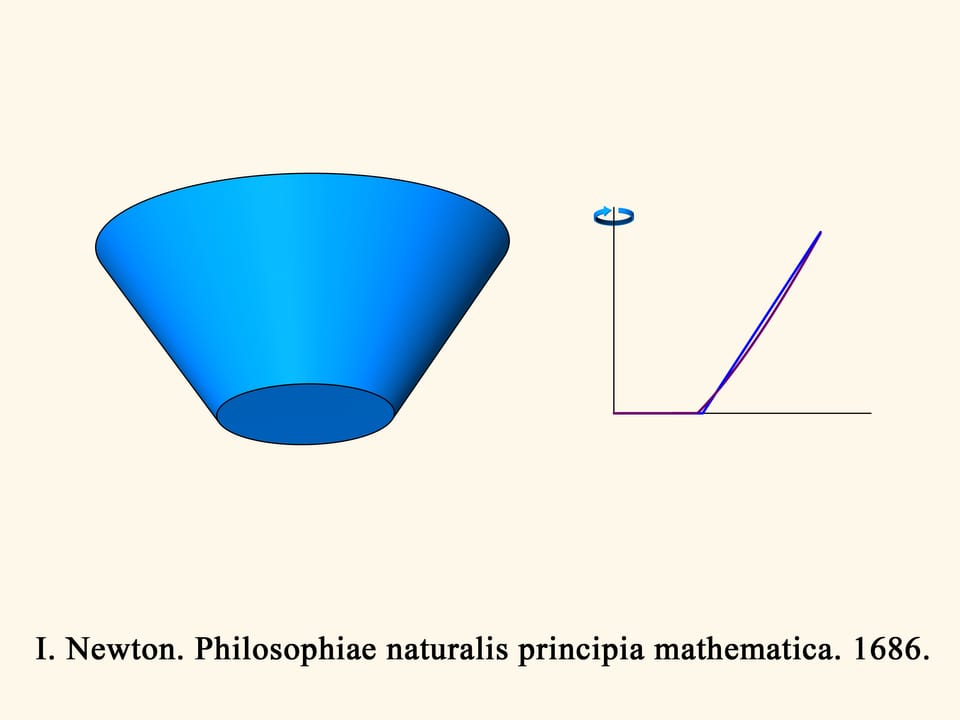
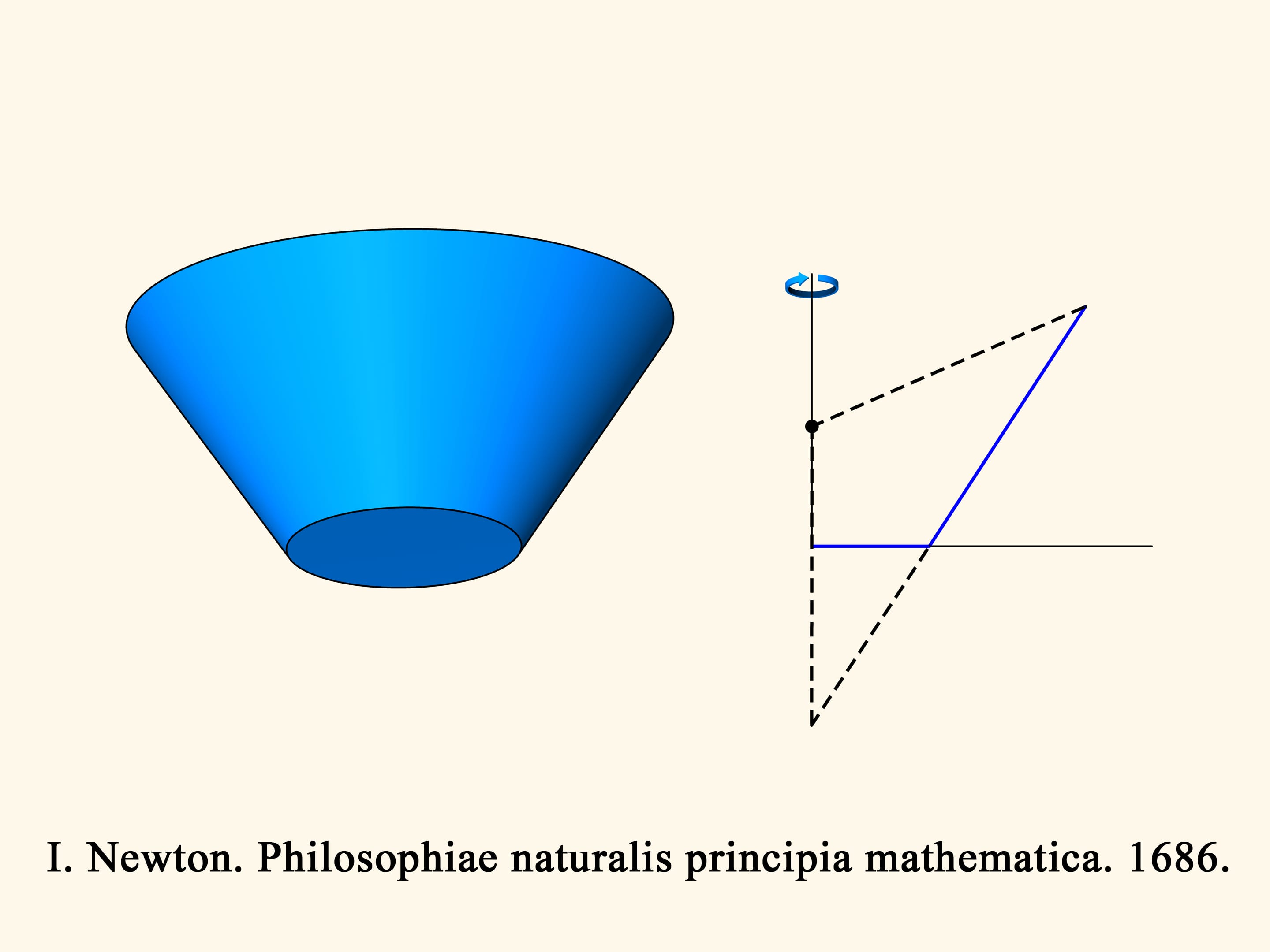
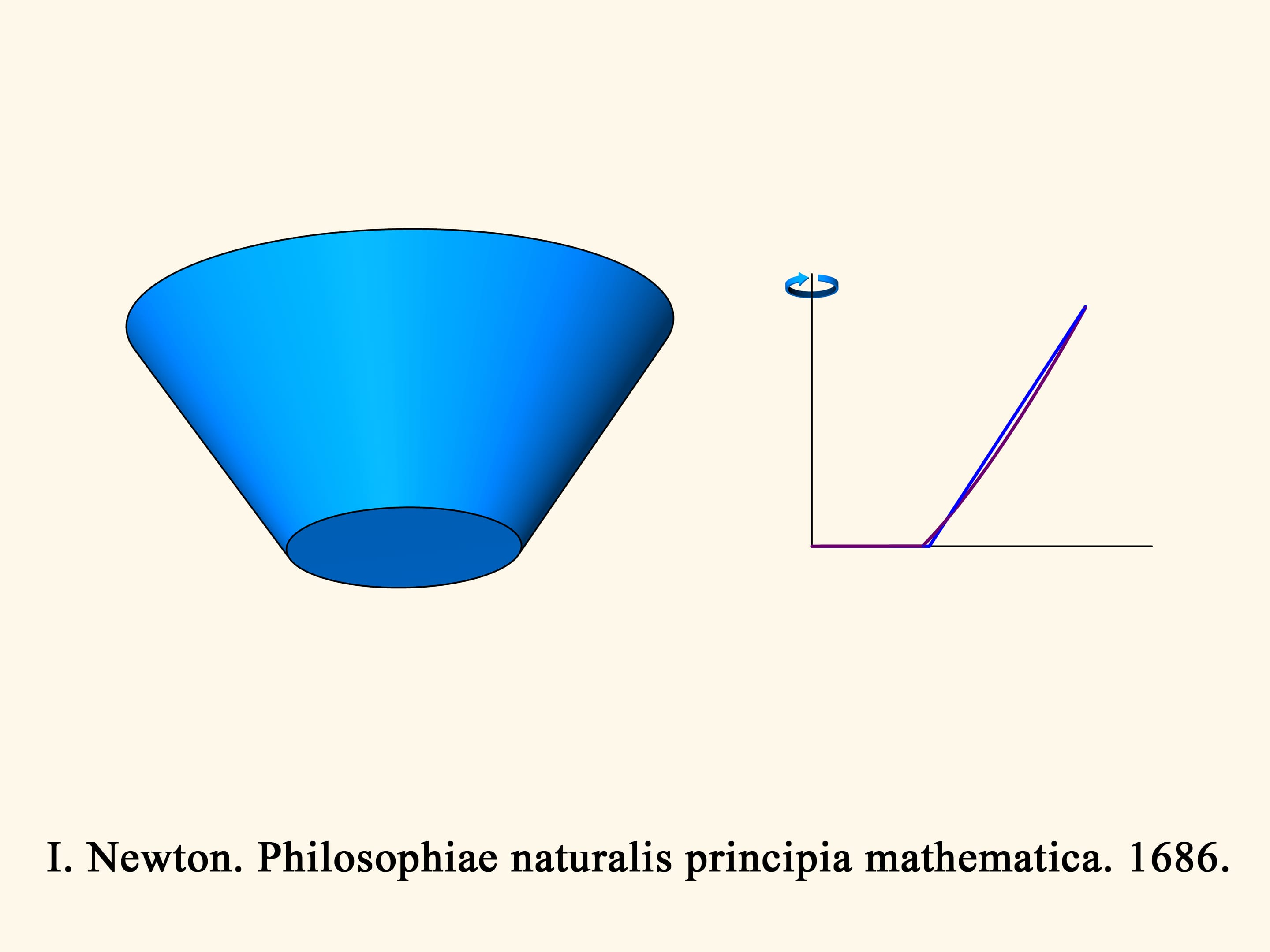
Dans le cas de trois dimen­sions, la résis­tance au cône tronqué en bleu est propor­tion­nelle au volume du corps solide en vert, et il faut trouver le minimum de ce volume, parmi tous les cônes tronqués. Newton montre que le cône tronqué sera optimal — c’est–à–dire, il rencontra la moindre résis­tance — à la condi­tion suivante. Prenons le point au milieu de la hauteur du trapèze et connec­tons le au point plus extrême de la base par un segment droit. Ajou­tons un segment vertical de cette longueur en dessous du point au milieu de l’hauteur. La géné­ra­trice du cône optimal est donnée par la base du triangle isocèle ainsi obtenu. Il est surpre­nant que le solide qui rencontre le moins de résis­tance n’est pas un cône mais un cône tronqué!

Mais quel sera le solide de révo­lu­tion convexe meilleur, dans le sens de la moindre résis­tance, avec une largeur et une hauteur données? Bien qu’à l’époque n’exis­tait pas encore de calcul varia­tionnel (ces problèmes main­te­nant sont résolus par cette méthode), Newton trouve la réponse à cette ques­tion. Il montre que le meilleure solide convexe de révo­lu­tion ne diffère pas beau­coup du cône opti­male, et calcule la courbe géné­ra­trice exacte de ce solide.

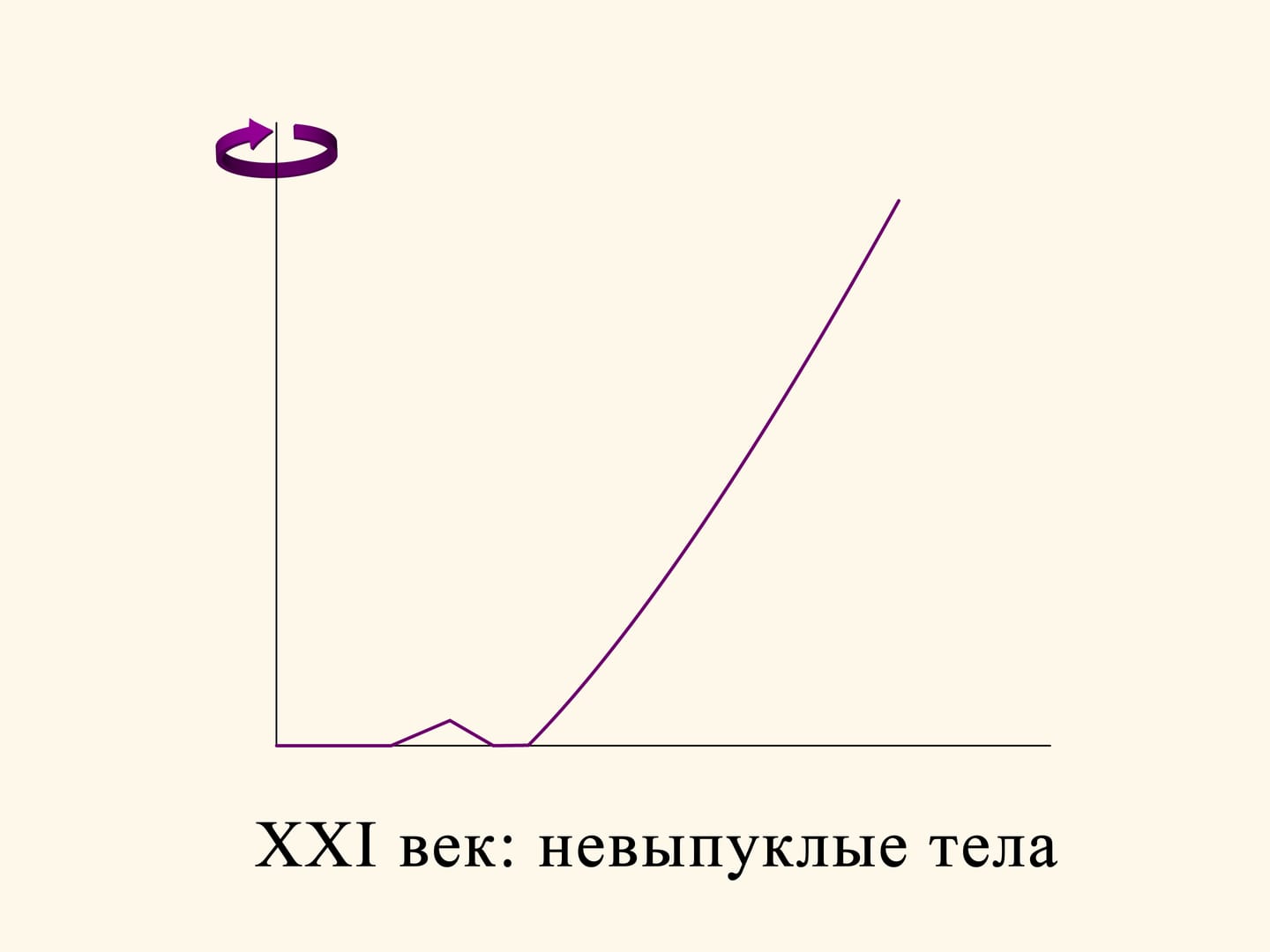
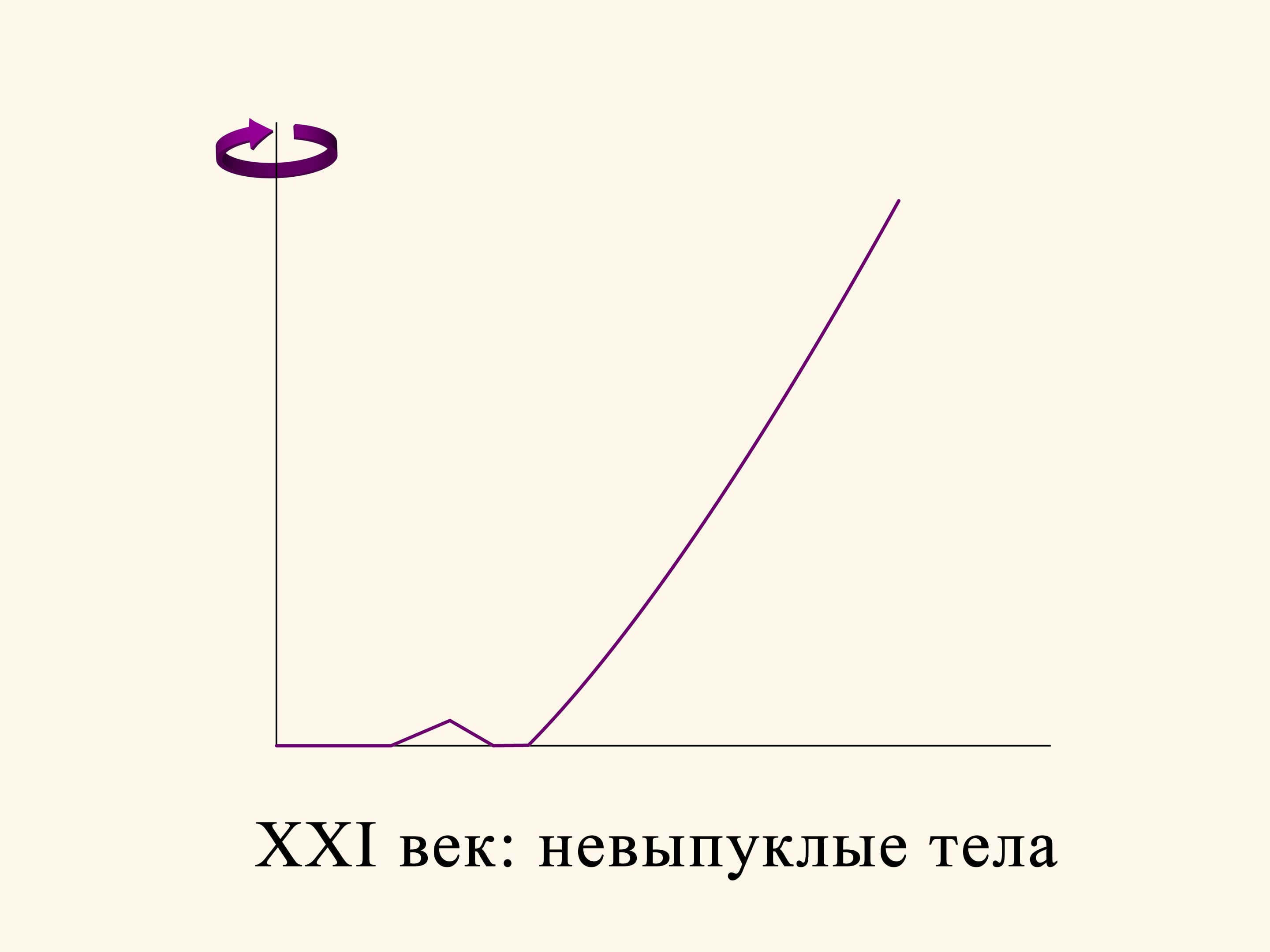
Depuis l’époque d’Isaac Newton, pour plus de 300 ans, les scien­ti­fiques ont étudié le problème aéro­dy­na­mique dans un milieu raréfié dans la même formu­la­tion initiale: trouver un solide convexe de révo­lu­tion. Il semblait naturel que le meilleur solide devait être convexe. Seule­ment dans le XXIe siècle les mathé­ma­ti­ciens ont essayé de renoncer à la condi­tion de convexité, et cela a conduit à un résultat incroyable!

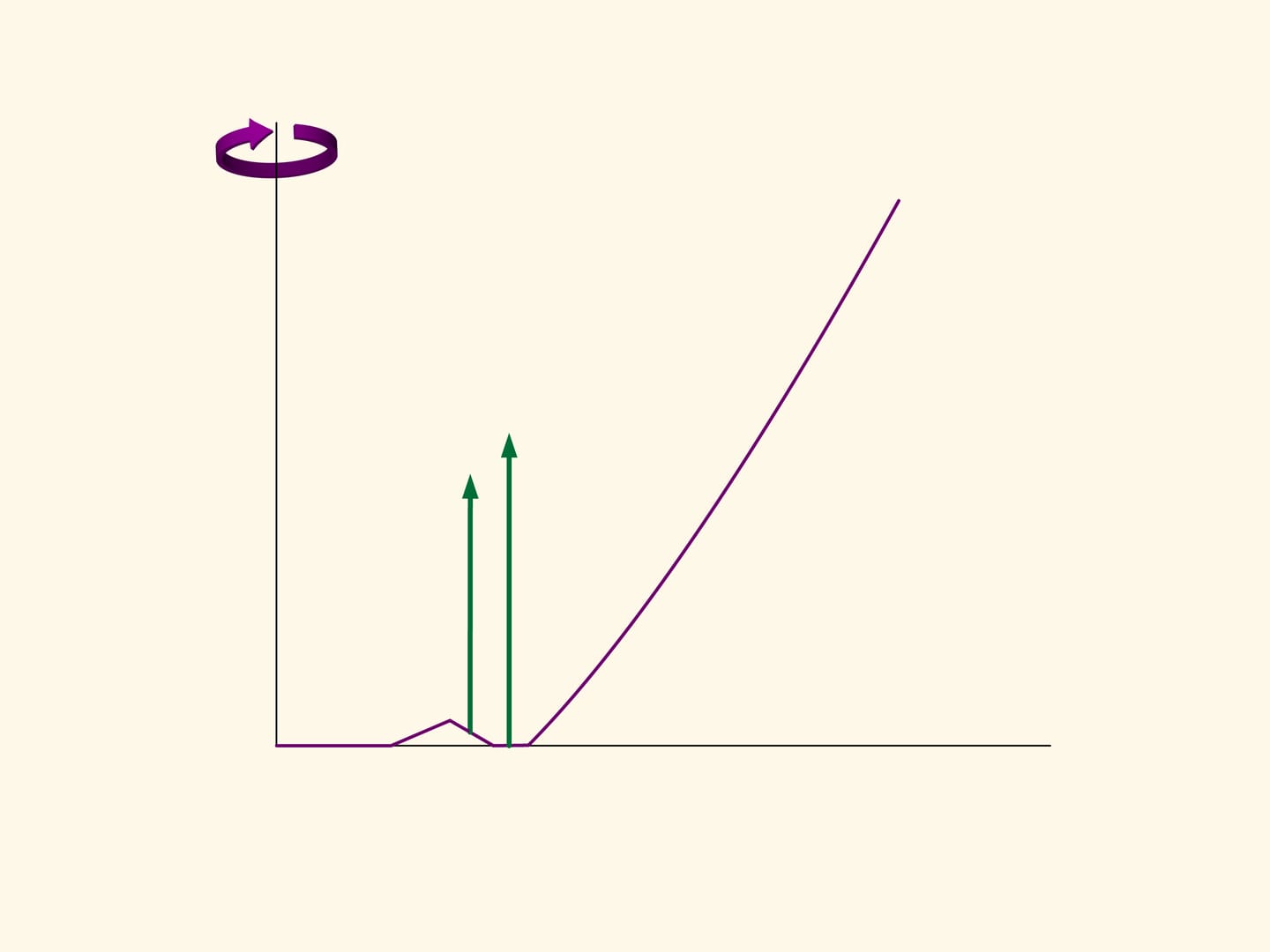
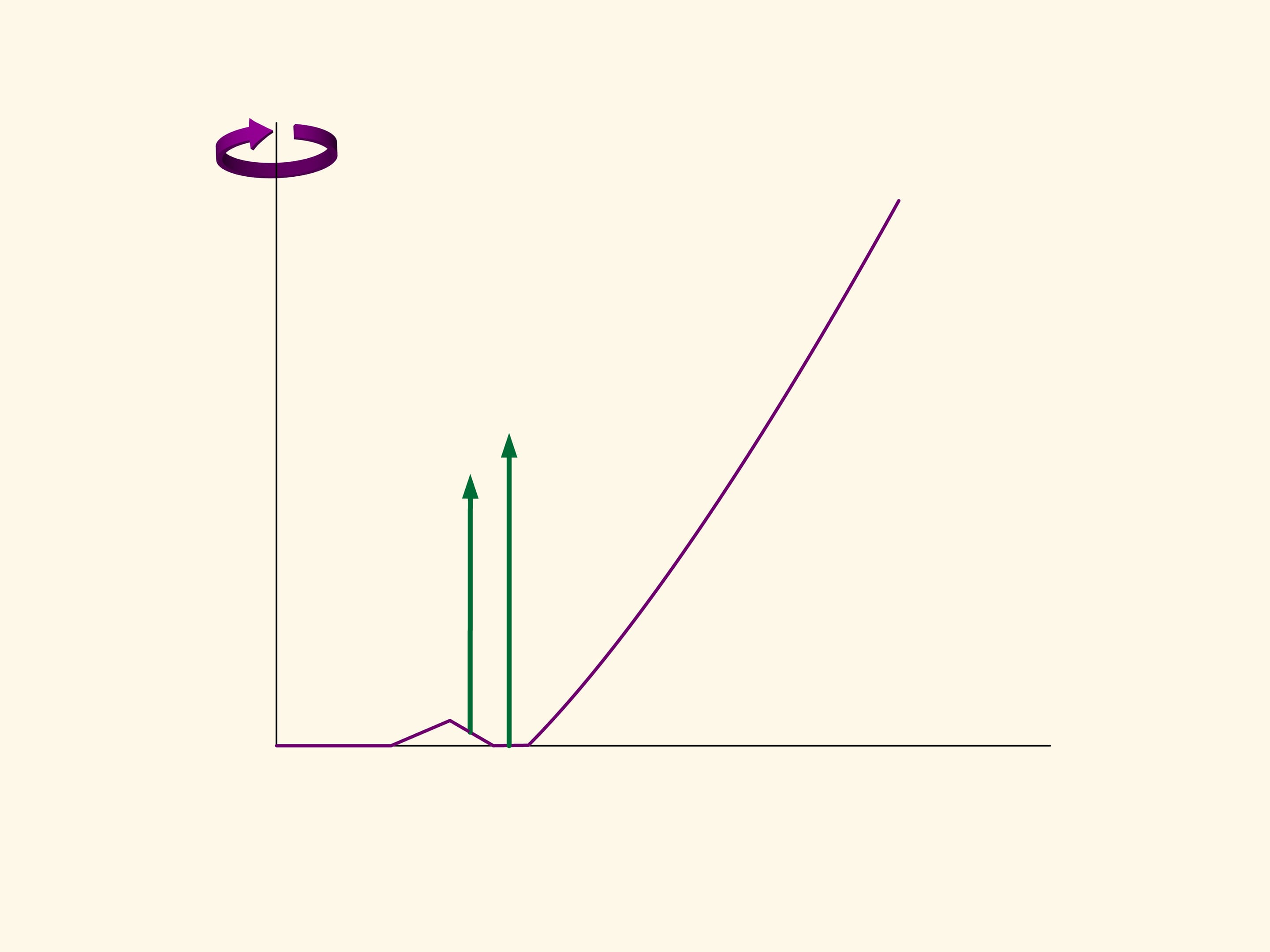
Prenons, par exemple, la section du solide optimal trouvé par Newton, et au milieu la partie plate faisons un trou trian­gu­laire. Le solide de révo­lu­tion obtenu n’est plus convexe, mais sa résis­tance diminue par rapport à celle du solide convexe. En fait, si la rainure n’est pas trop profonde, une sphère, après l’avoir heurté rebondit en direc­tion oblique et n’entre plus en colli­sion avec le solide. La compo­sante verti­cale du vecteur impul­sion de la sphère, et, par consé­quent, le frei­nage dû à la colli­sion sera plus faible que pour un rebond sur une surface hori­zon­tale.

Nous allons observer deux construc­tions inté­res­santes de solides non convexes, expo­sées dans le travail de A. Yu. Plakhov.

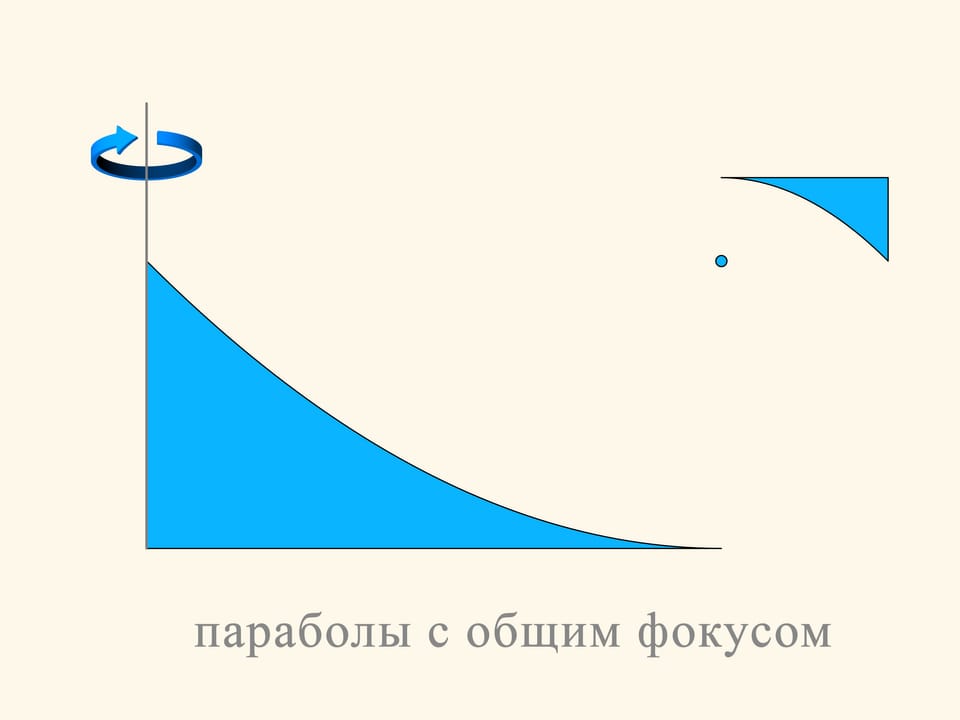
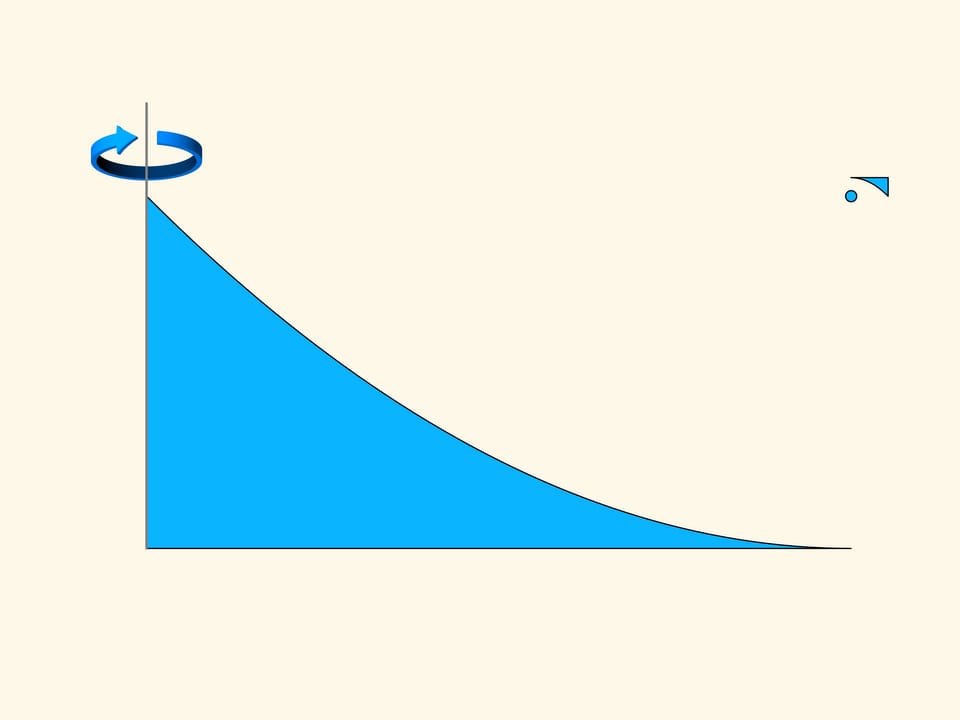
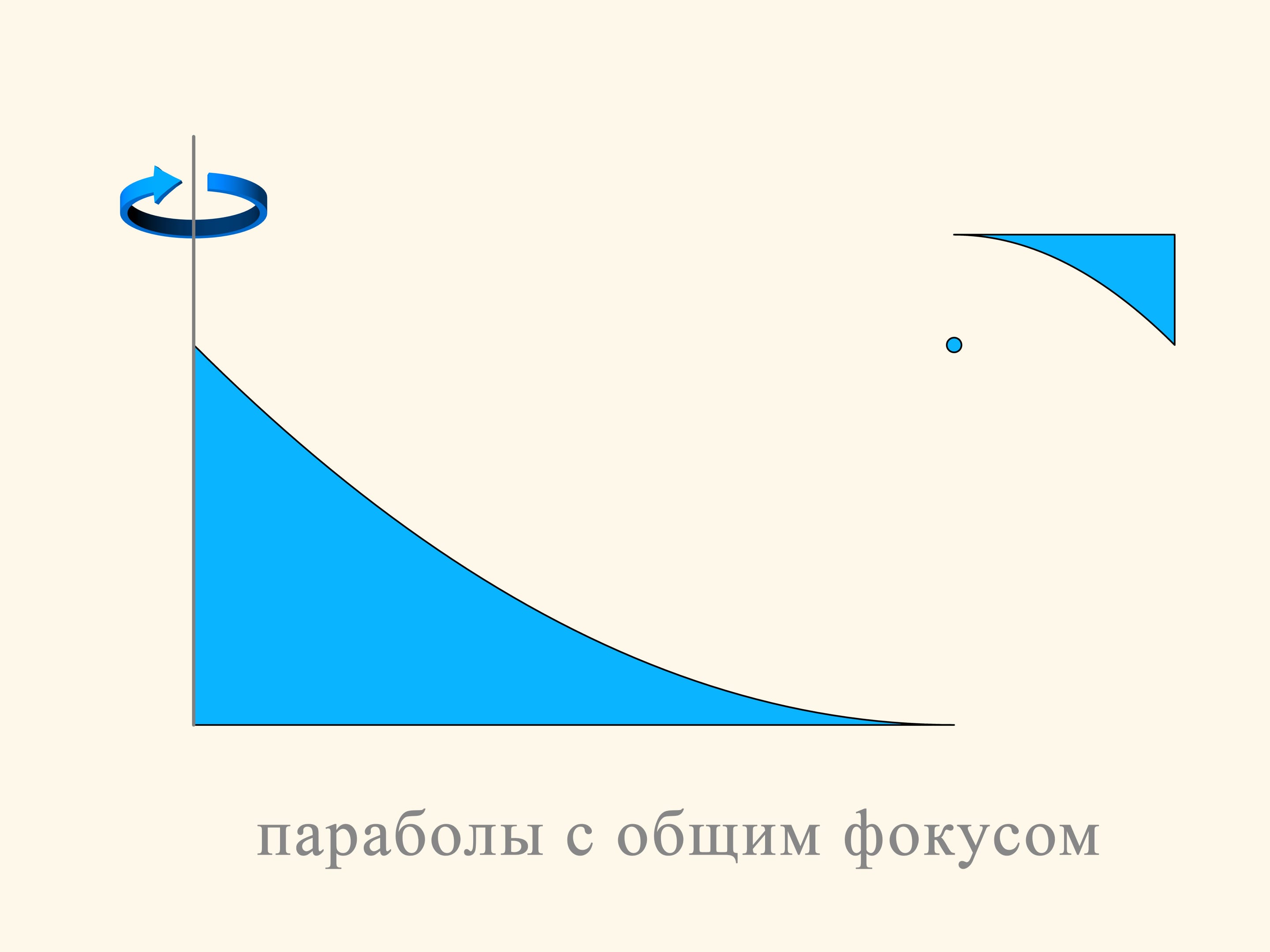
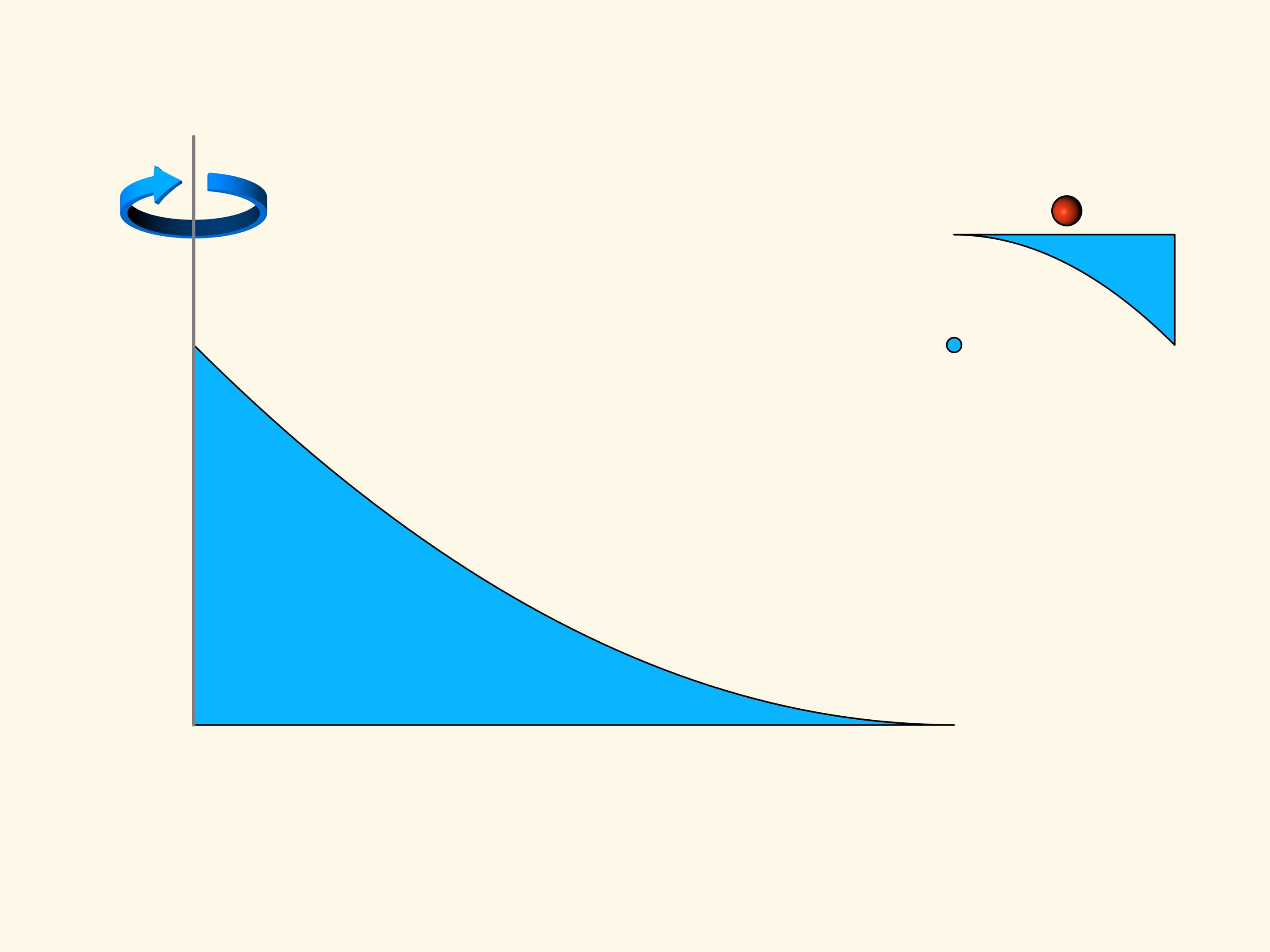
La section du premier solide se compose de deux morceaux de para­boles, placées dans le plan de façon que leurs foyers et leurs axes coïn­cident. Le mouve­ment sera dans la direc­tion des axes des para­boles. Comme vous le savez, la para­bole a la propriété optique que les rayons paral­lèles à son axe, après réflexion sur la para­bole passant par son foyer. Dans la construc­tion consi­dérée, une partie des sphères qu’elle rencontre, tombe dans la petite partie hori­zon­tale tangente à la petite para­bole et oppose une résis­tance au mouve­ment. Mais la plupart des sphères sont reflé­tées par la para­bole plus grande, passent par le foyer, puis sont reflé­tées par la para­bole plus petite, et s’en vont dans une direc­tion paral­lèle à celle initiale. Dans le milieu raréfié de Newton ces sphères n’augmentent pas la résis­tance parce qu’elles ne perdent pas la compo­sante verti­cale de l’impul­sion, et après les colli­sions elles sortent dans une direc­tion paral­lèle à celle avec laquelle elles étaient entrées, seule­ment déplacée en hori­zon­tale.

La partie du solide qui reflète les sphères peut être réduite, sans altérer l’idée de base de sa construc­tion.

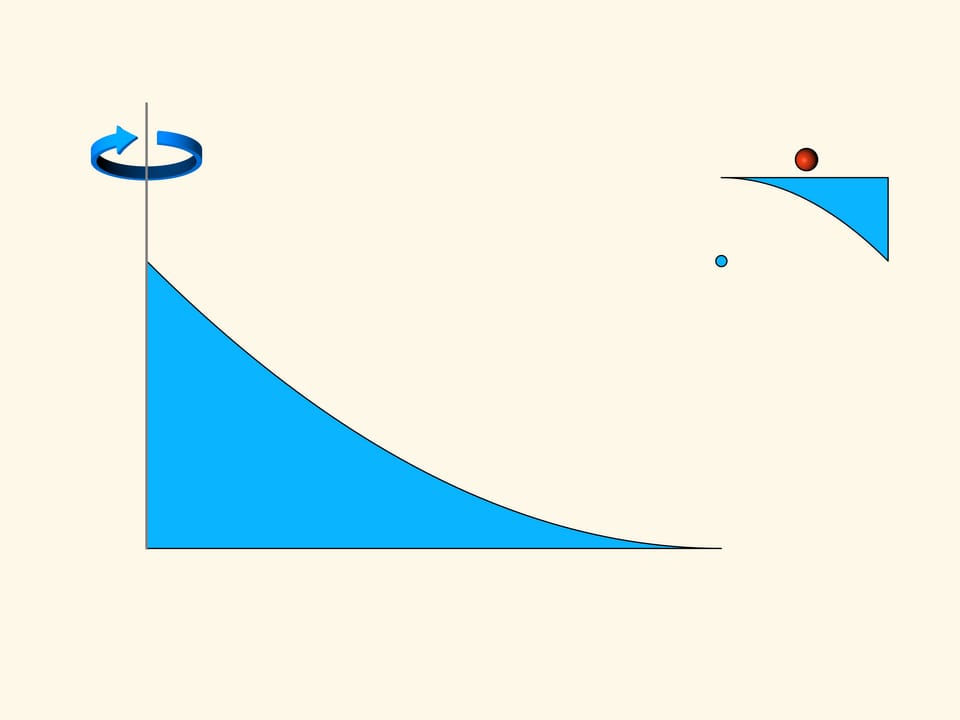
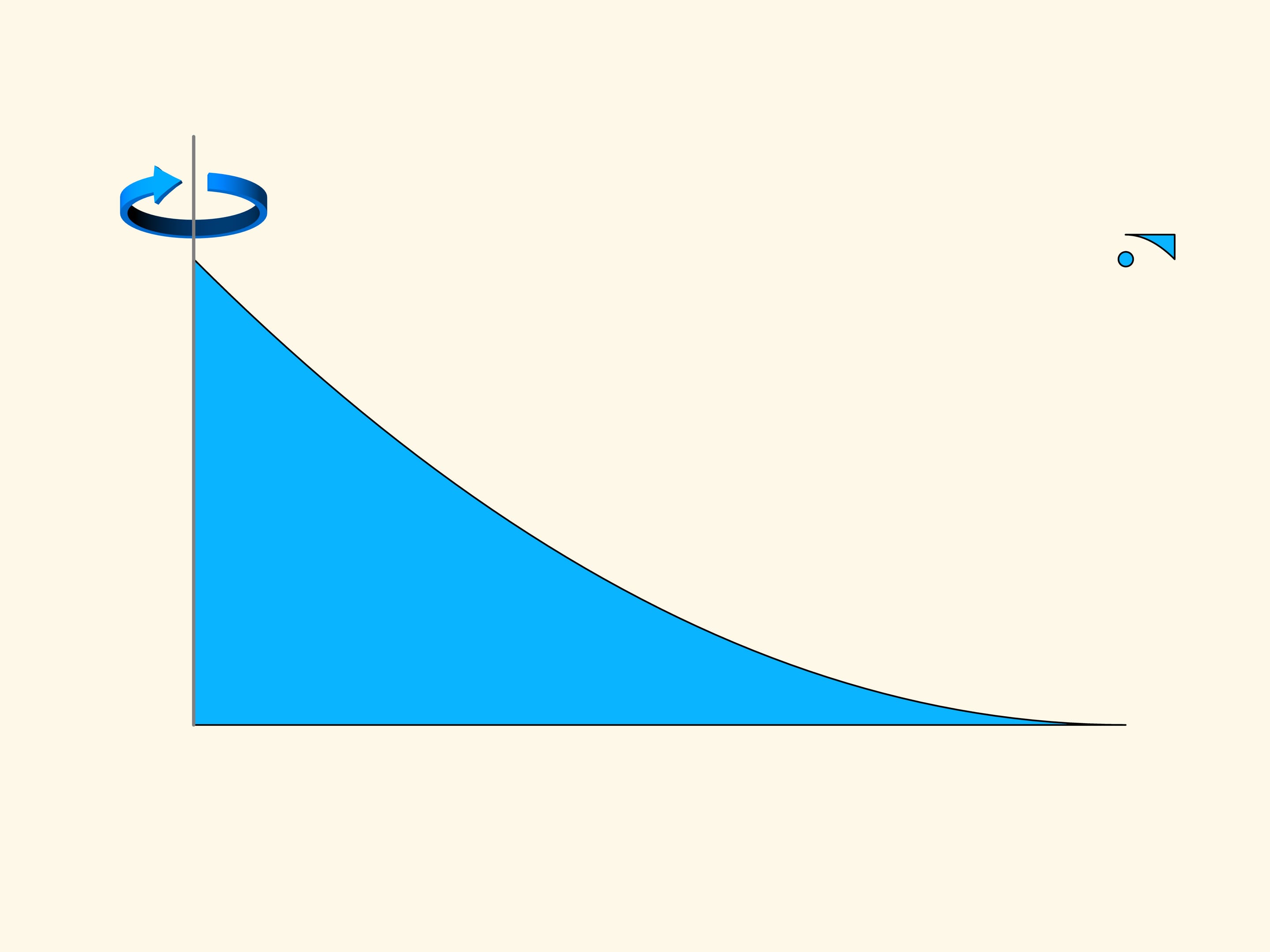
Nous faisons tourner la construc­tion des deux para­boles autour de l’axe vertical. On obtient un solide qui nous rappelle une soucoupe volante. Si l’on regarde de dessus, on voit que la surface de ce disque est très grand. La surface qui oppose une résis­tance on peut la rendre autant petite que l’on veut. Pour un mouve­ment dans la direc­tion de son axe de révo­lu­tion ce solide dans un milieu raréfié de Newton rencon­trera une résis­tance arbi­trai­re­ment petite.

Mais y a–t–il des corps solides sans résis­tance du tous? Il arrive qu’il y a aussi ceux–là!

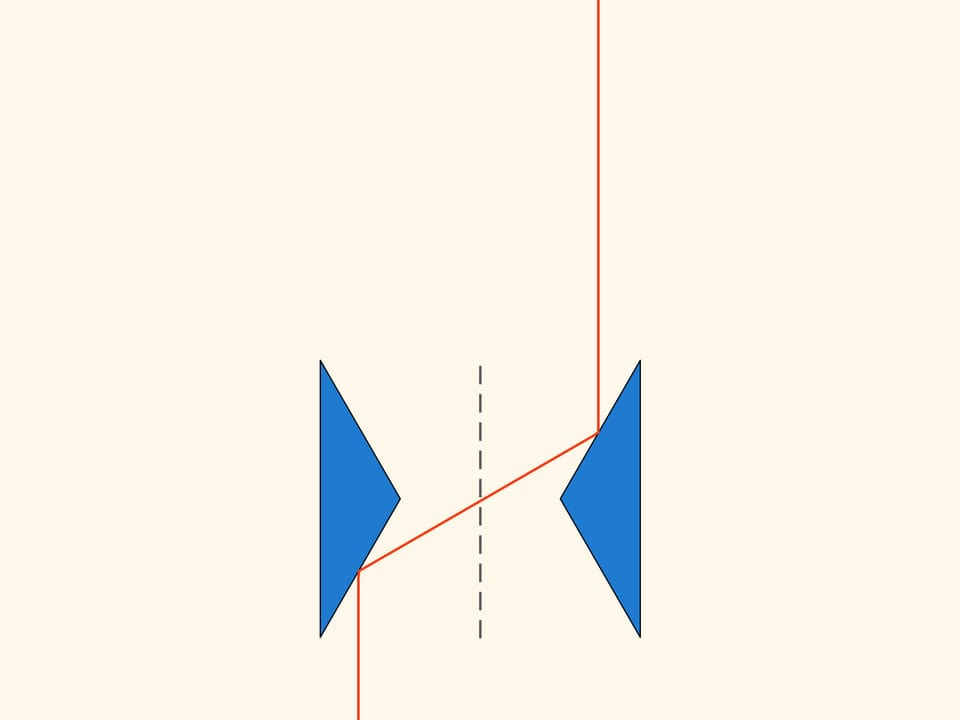
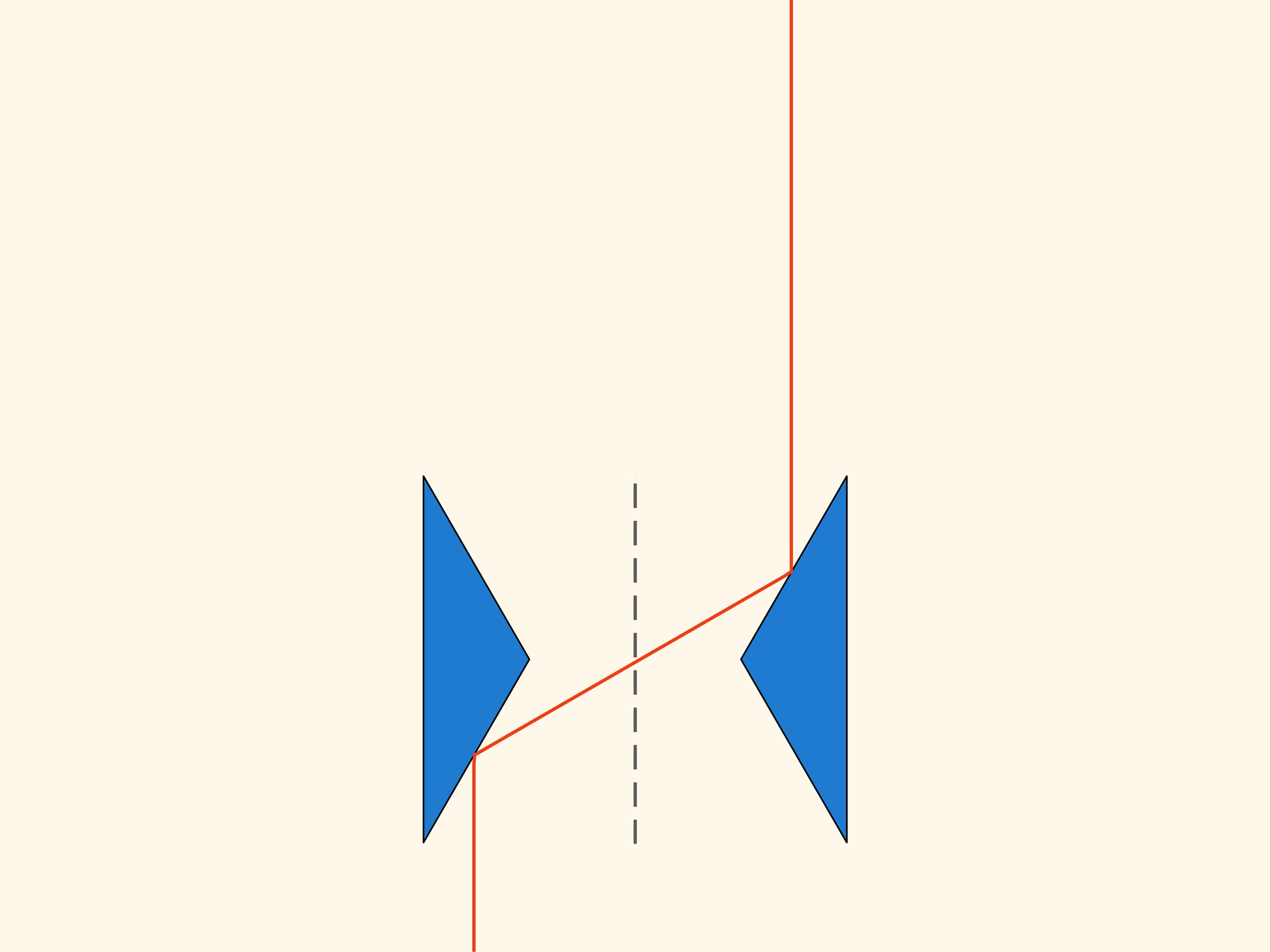
La construc­tion est basée sur un triangle avec des angles de degrés 30, 30 et 120. Prenons un autre triangle symé­trique par rapport à l’axe vertical et à une distance de deux hauteurs.

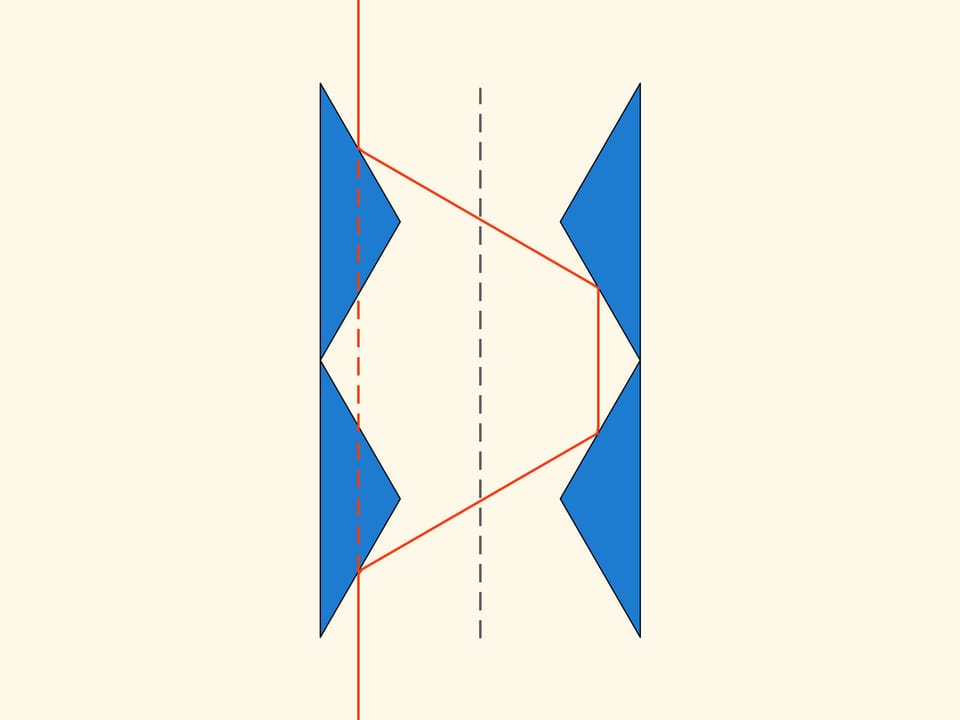
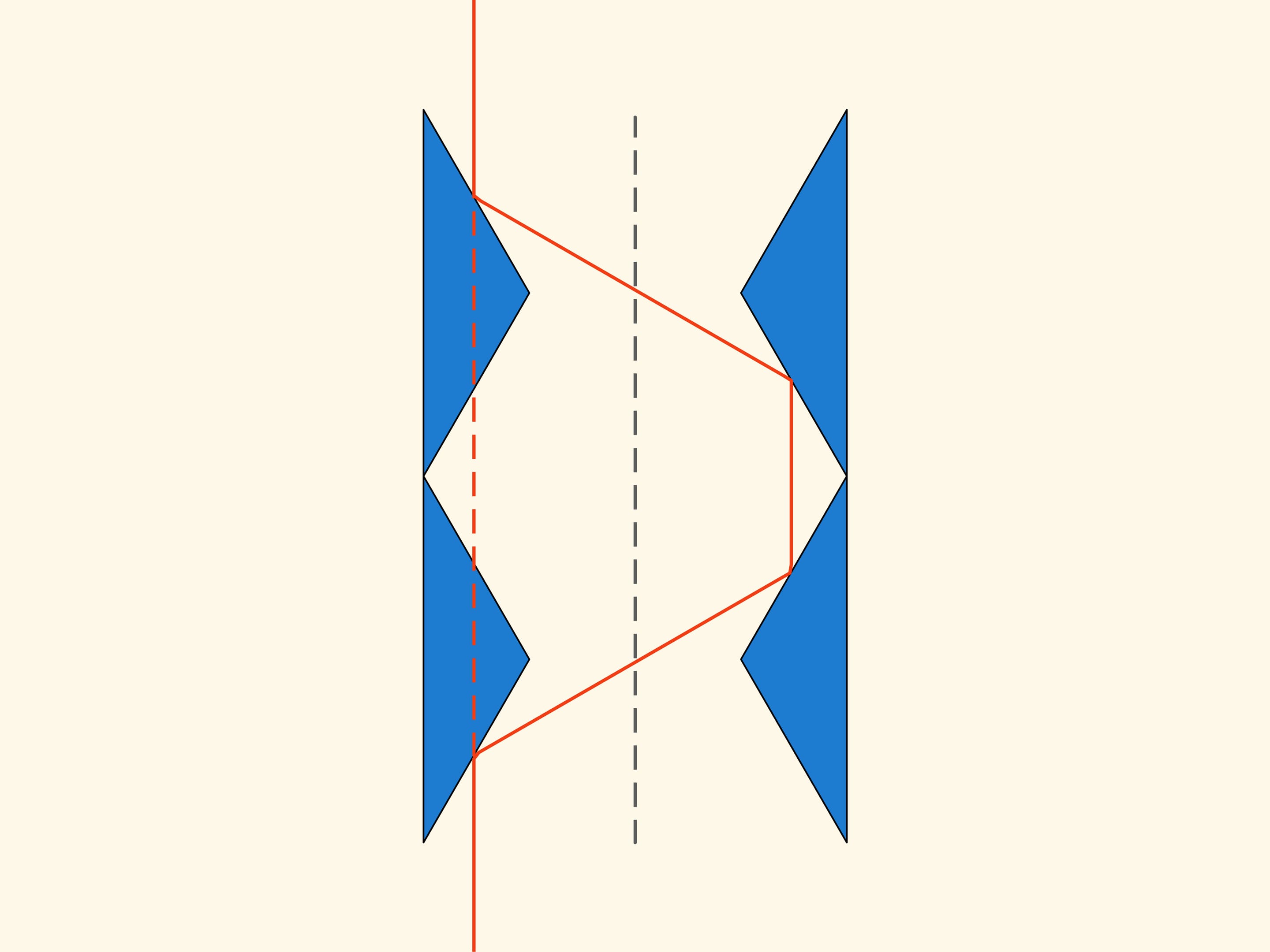
Obser­vons ce qui arrive quand cette construc­tion plane se déplace dans la direc­tion de l’axe de symé­trie dans un milieu raréfié de Newton. Certaines sphères ne l’heurtent pas du tout, et ces parti­cules n’ont aucune influence sur le mouve­ment. Mais les sphères, avec lesquelles elle entre en colli­sion, sont toujours reflé­tées par tous les deux triangles et sortent dans une direc­tion paral­lèle à l’axe de symé­trie, sans changer leur impul­sion. De cette façon, la résis­tance du solide obtenu par rota­tion autour de l’axe de symé­trie de cette construc­tion, est égal à zéro!

Pour suivre la trajec­toire des sphères — les parti­cules du milieu — nous avons repré­senté leurs trajec­toires en forme de rayons. Mais c’est exac­te­ment le long de cette trajec­toire qu’un rayon de lumière se propage! Si la dernière construc­tion basée sur deux triangles est constitué de surfaces réflé­chis­santes, les parties droite et gauche des images que nous voyons à travers d’elle, résultent échan­gées. Mais si nous prenons une deuxième construc­tion égale à la première et la plaçons au dessus de la première, alors les rayons qui passe­ront à travers du système optique ainsi obtenu ne résul­te­ront ni déviés, ni inversé.

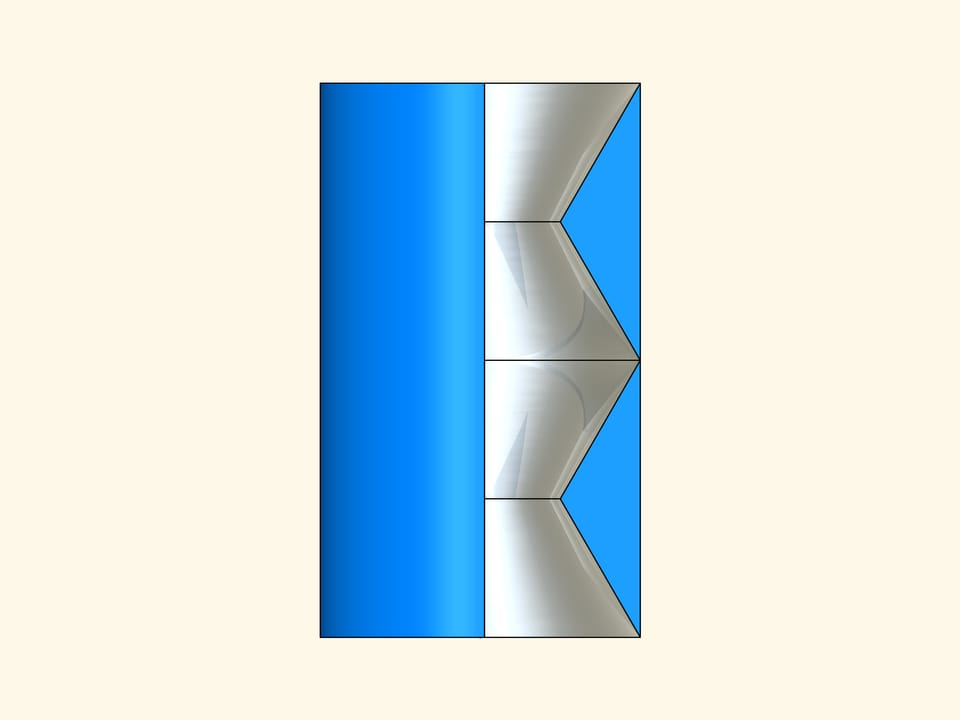
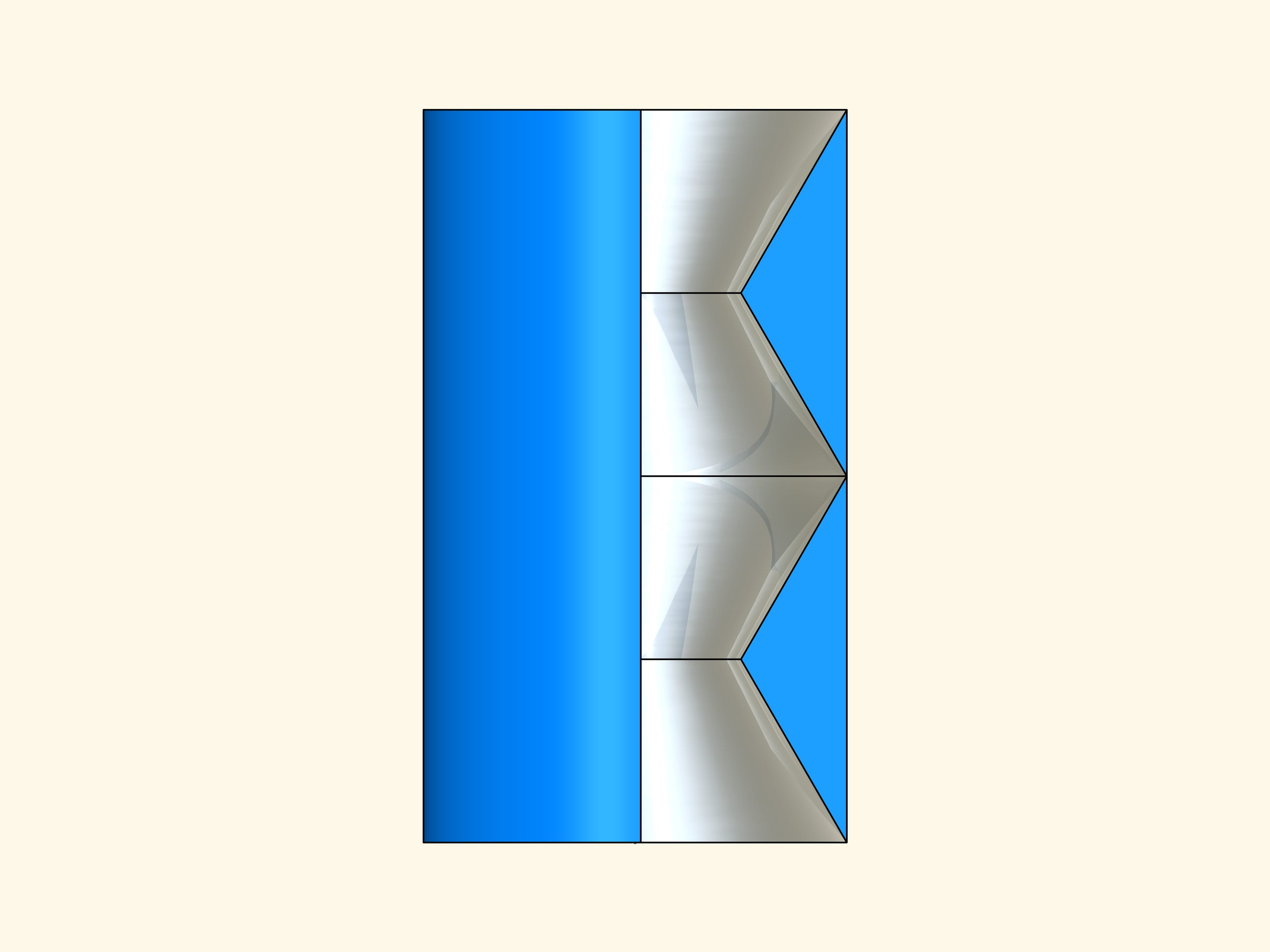
Faisons tourner notre construc­tion planaire autour de son axe de symé­trie et suppo­sons que toutes les surfaces internes sont des surfaces–miroir. Nous obte­nons un solide qui exté­rieu­re­ment est un cylindre mais à l’inté­rieur est constitué de quatre cônes tronqués aux surfaces réflé­chis­santes. Si nous regar­dons à travers ce cylindre en direc­tion de son axe de symé­trie, alors il sera invi­sible!

Dans son travail, A.Yu.Plakhov a aussi consi­déré comment faire un manteau invi­sible pour un corps arbi­traire. Un objet recou­vert d’un manteau semblable devient presque invi­sible!

Évidem­ment, ces construc­tions ne dévient pas (ou presque ne dévient pas dans le cas du manteau invi­sible) seule­ment les rayons qui sont paral­lèles à l’axe de symé­trie. Et pour l’oeil humain le «cylindre invi­sible» en effet sera presque invi­sibles seule­ment si regardé d’assez loin. Il est possible que certains d’entre vous, en utili­sant la connais­sance des mathé­ma­tiques, et, éven­tuel­le­ment, d’autres sciences, à l’avenir seront en mesure de construire des objets tota­le­ment invi­sible.