Vivant à la surface de la Terre, les individus ont considéré pendant longtemps qu’elle était plate. Il a fallu l’approfondissement des théories scientifiques pour prouver que la Terre ressemblait à une sphère.
Ainsi, en mathématiques, “sortant dans la surface volumique”, on peut, en partie, connaître de nombreuses choses intéressantes sur l’objet.
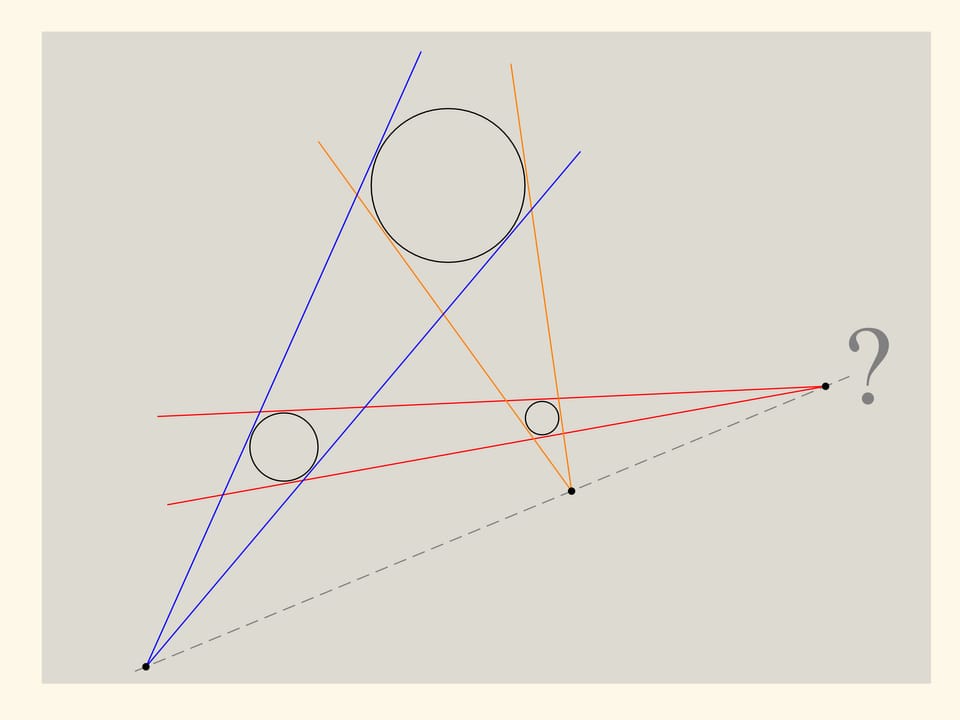
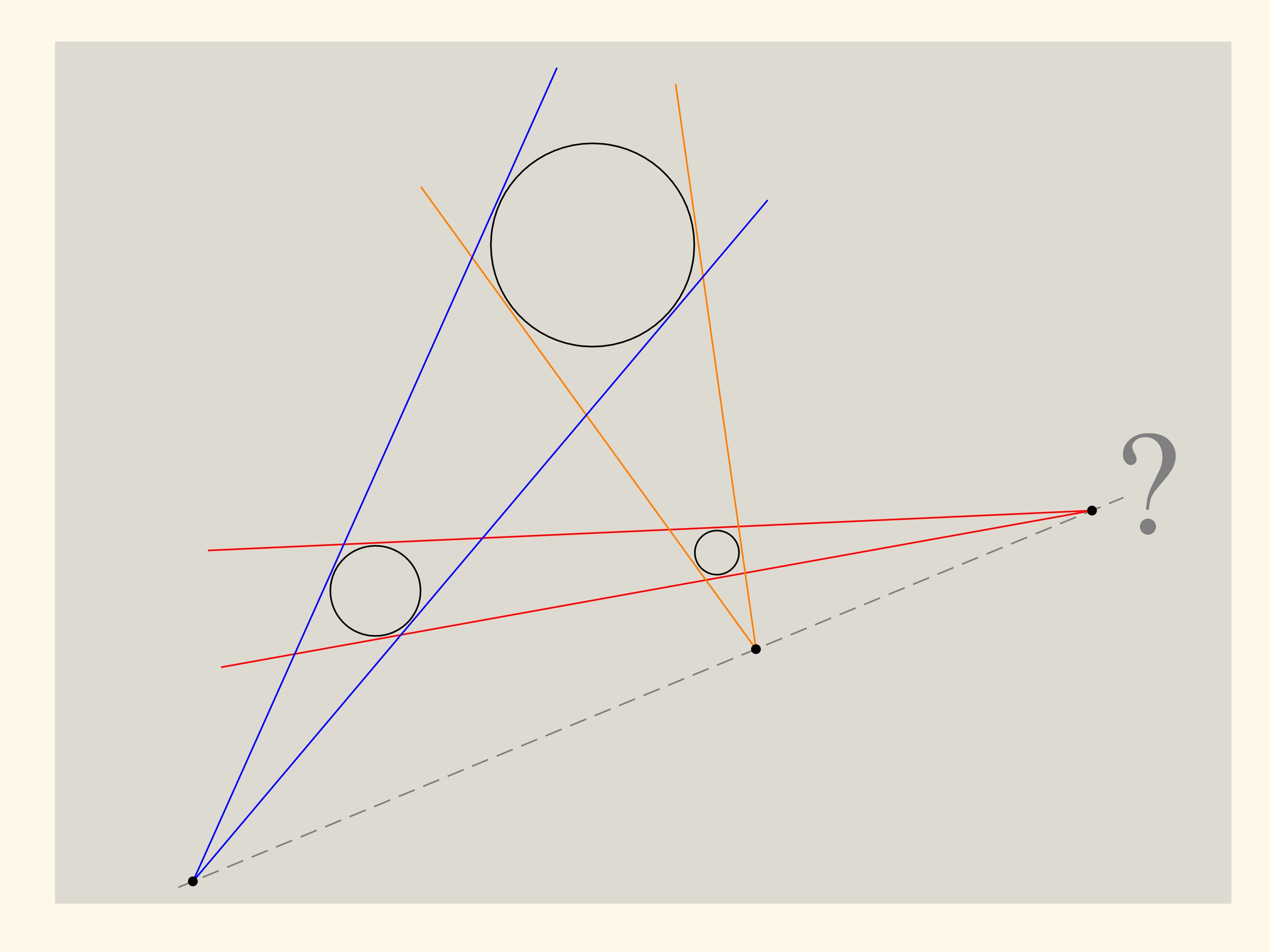
Prenons trois circonférences quelconques, et faisons les se toucher deux par deux, à chaque paire de circonférences. Que peut-on dire des trois points obtenus, dont l’intersection semble conduire vers deux circonférences? A en juger par le dessin, ils se situent sur une même droite. Cependant, le dessin n’est pas une démonstration, mais une simple information pour l’élaboration d’une hypothèse. Essayons de la démontrer.
Le problème posé et le dessin sont sur un plan. Observons ce plan de l’intérieur: d’un espace en 3D.
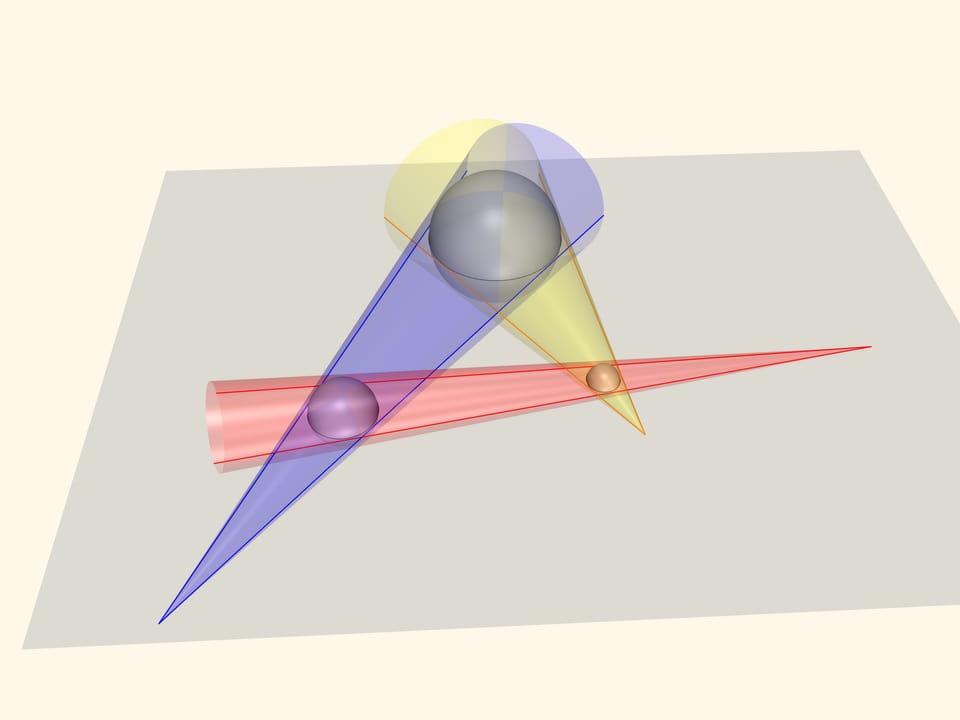
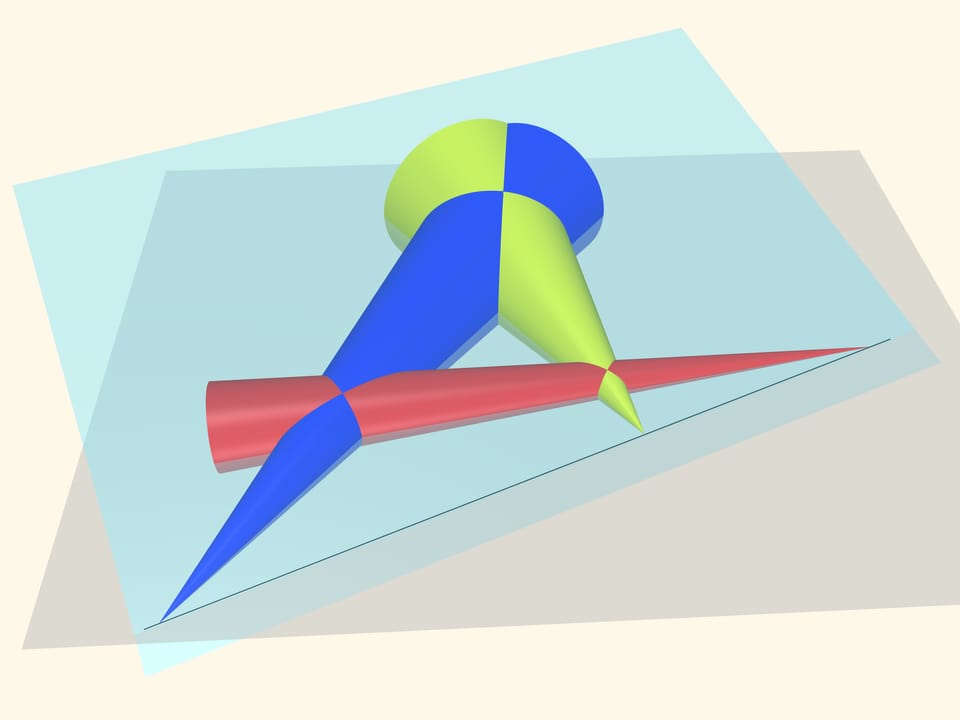
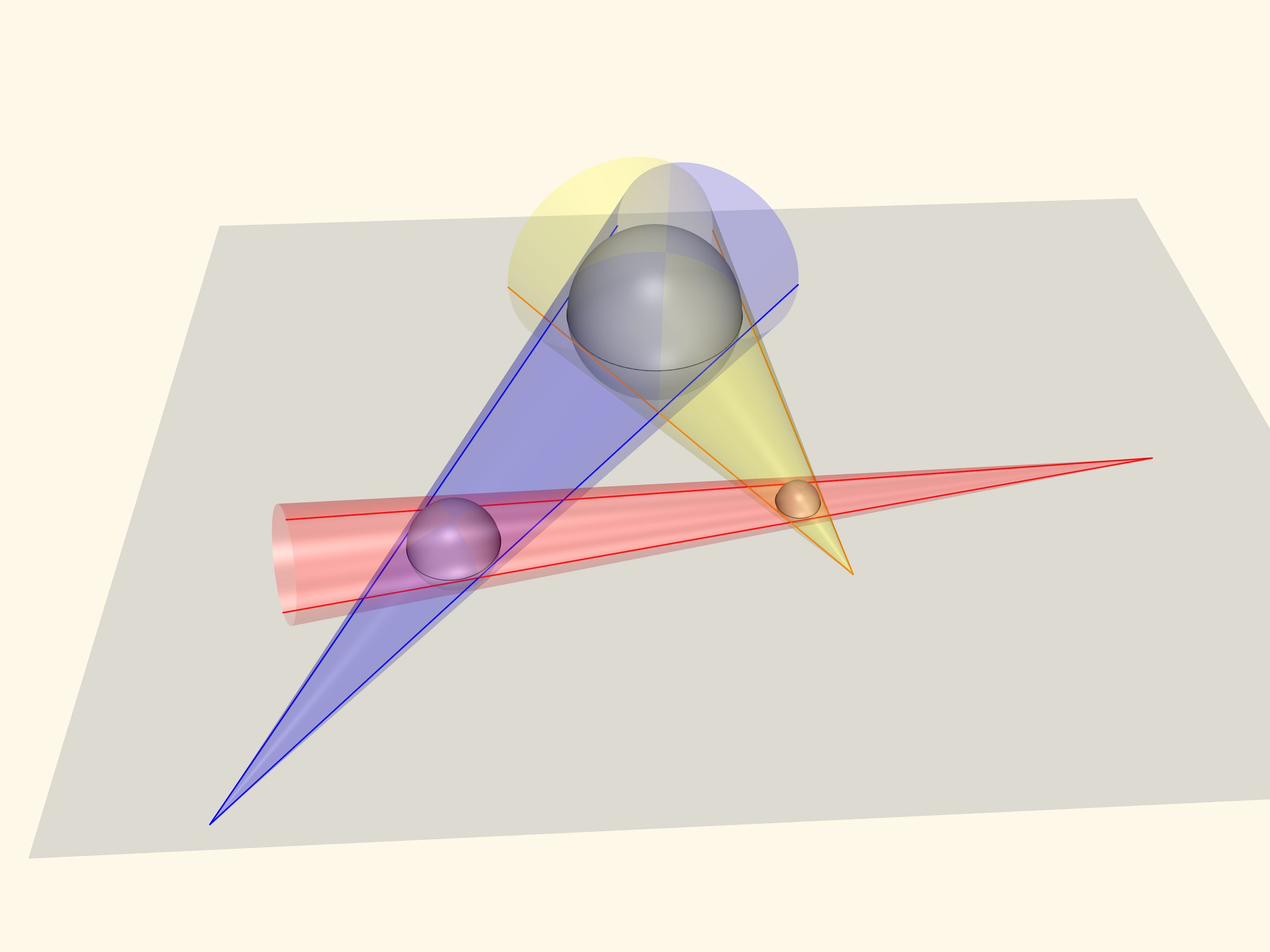
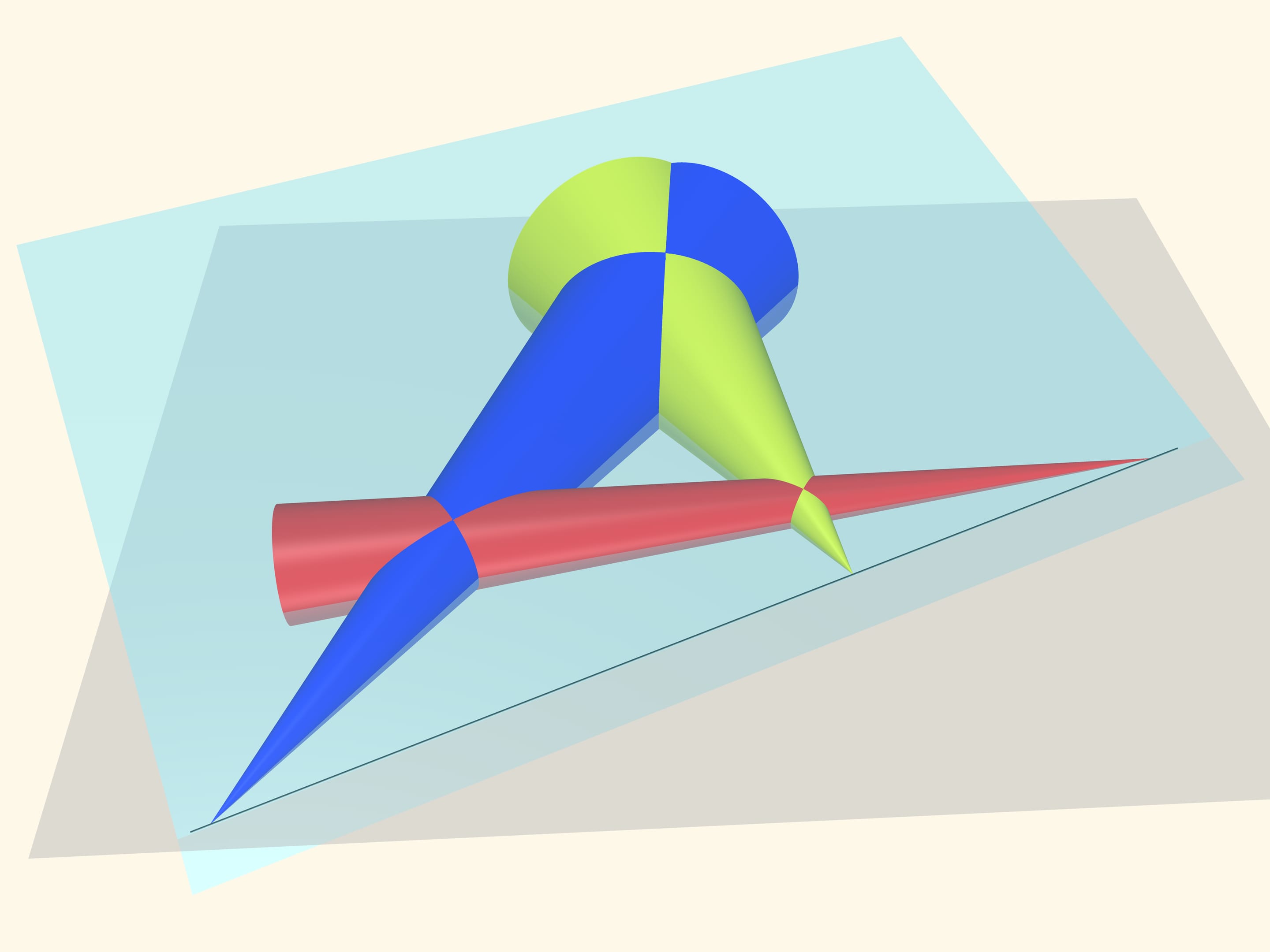
Prenons trois sphères dont la circonférence apparaît d’abord comme des équateurs. Des cônes, deux par deux, des sphères suffisantes, ainsi formés, vont avoir du sens dans la démonstration.
Les points qui sont alignés sur une même droite selon notre hypothèse, seront les sommets des cônes. On place un plan sur les cônes. Les sommets des cônes se croisent deux à deux et forment un plan unique. Les points qui nous intéressent sont les sommets des cônes, et appartiennent à ce plan, tout comme au plan initial: “le plan équatorial”. Deux plans, non parallèles, se croisent en une droite. Cela signifie, comme on l’a suggéré, que ces trois points se croisent.
On a, à présent, démontré le théorème portant le nom d’un mathématicien français: Gaspard Monge.
Autres études dans en “D’autres sujets interessants”
