Le triangle recourbé de Reuleaux ⁠

Cette anima­tion montre comment un concept géomé­trique, étudié par les mathé­ma­ti­ciens, est utilisé dans notre vie quoti­dienne.

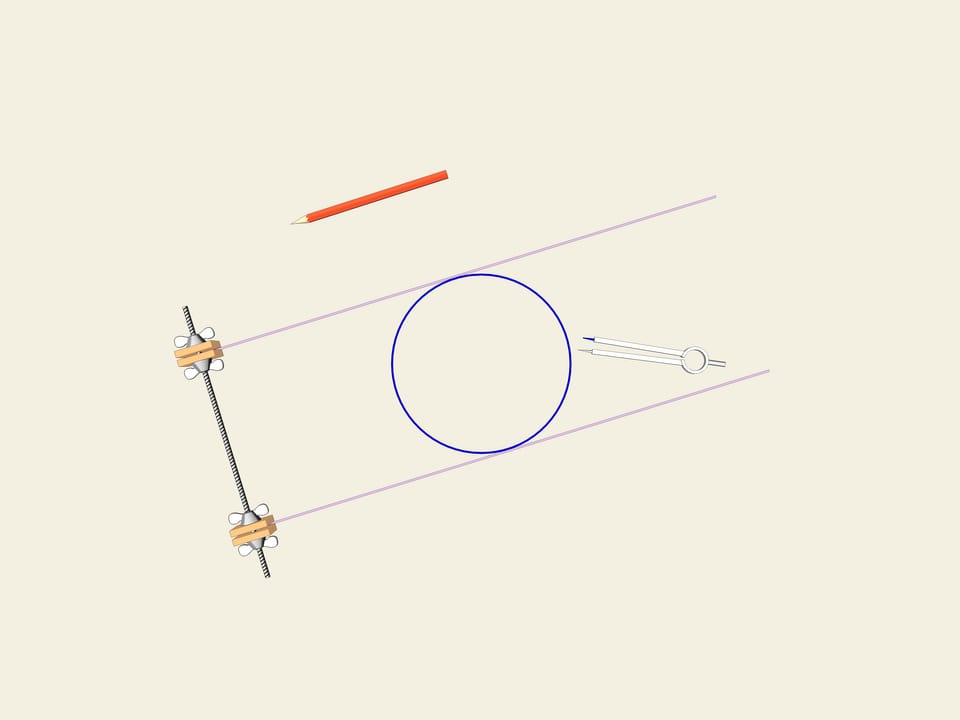
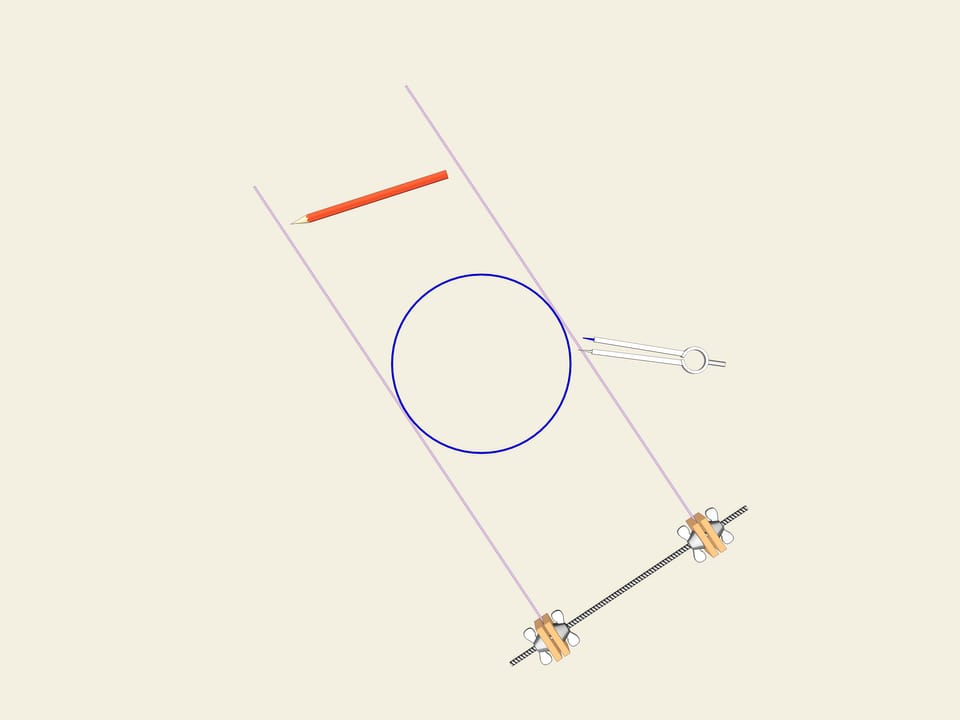
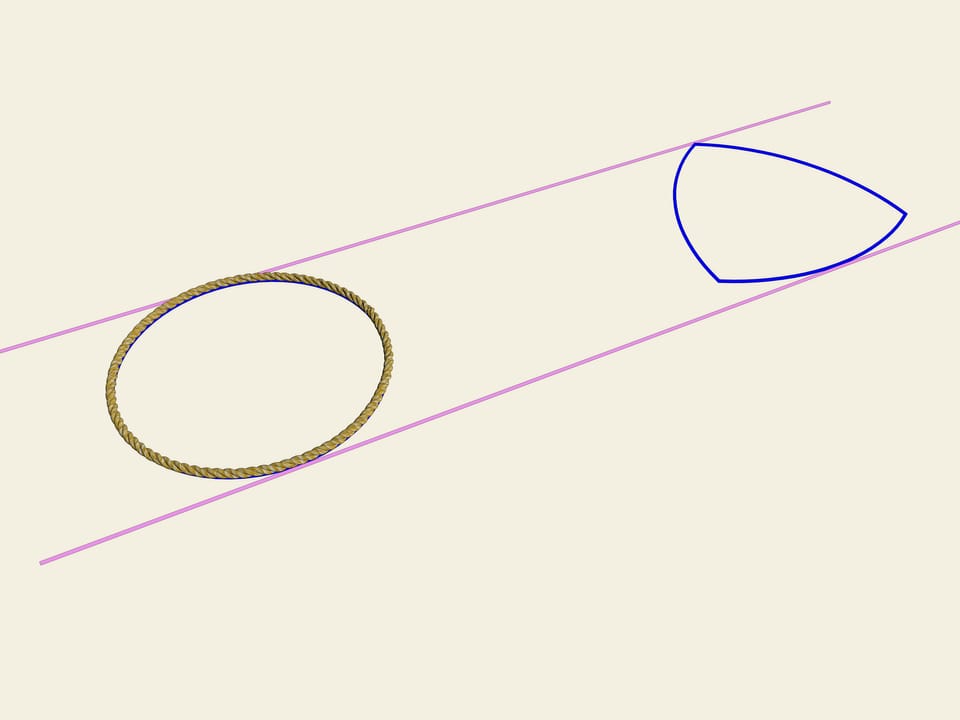
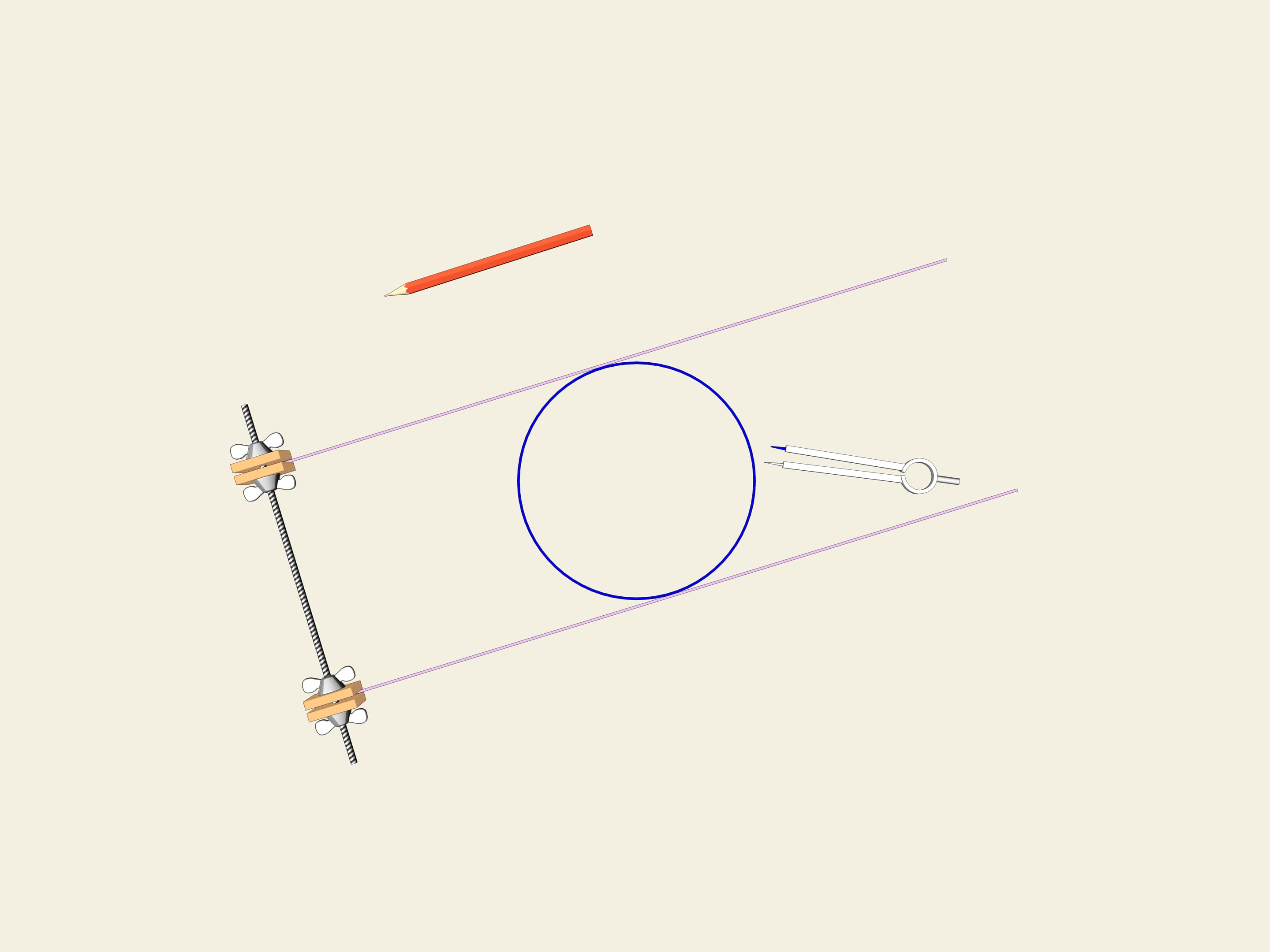
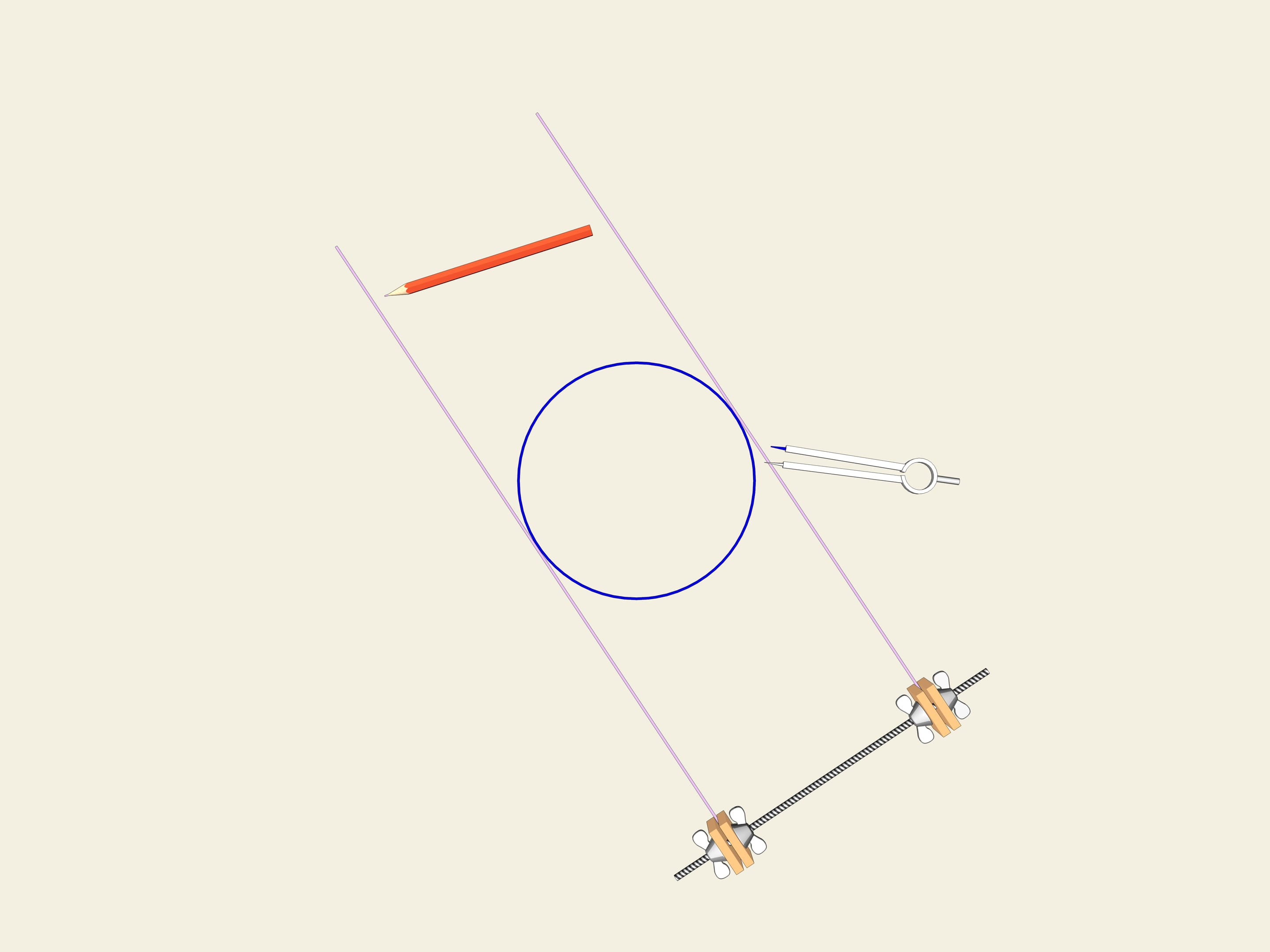
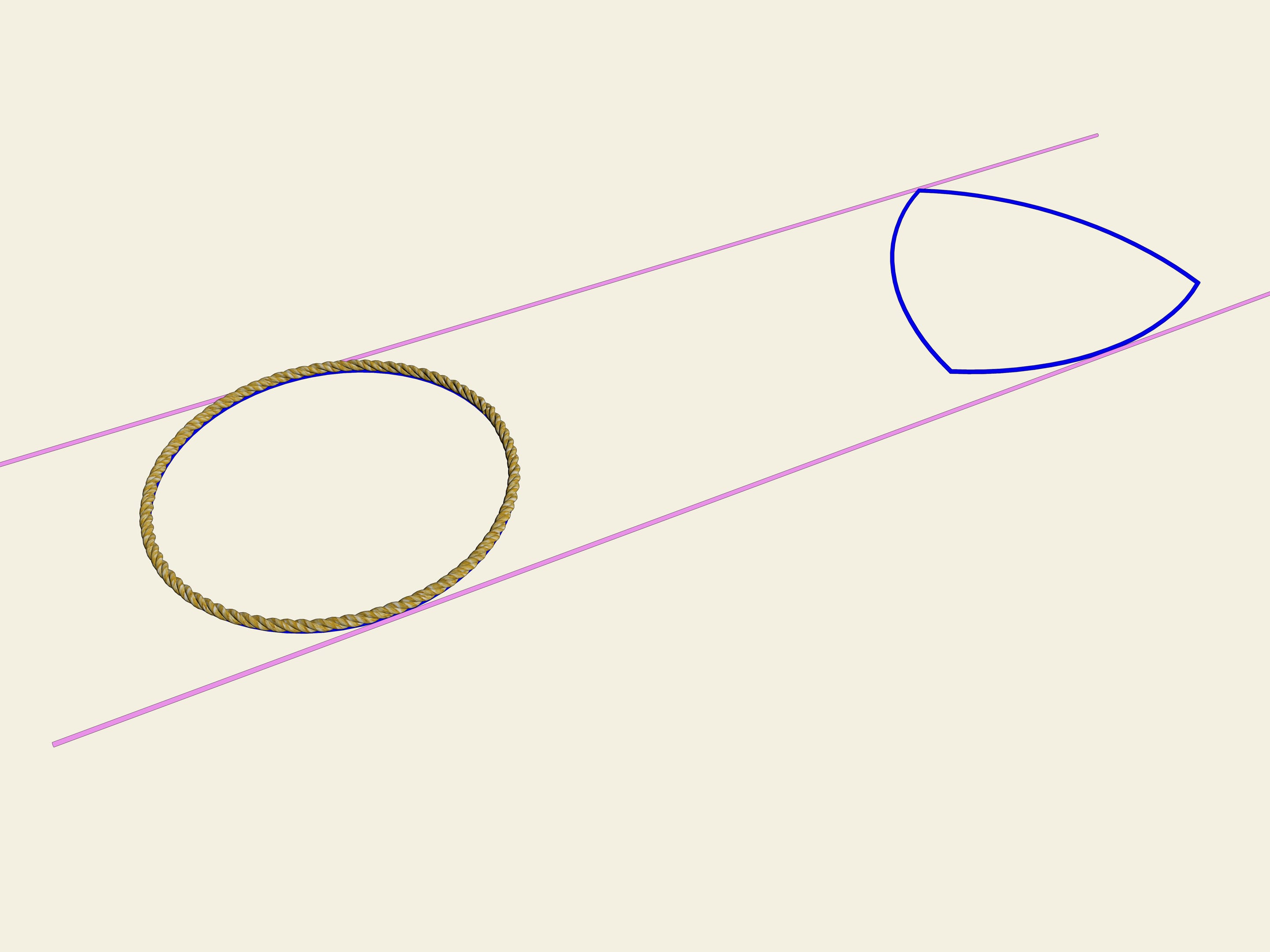
Prenons une roue, c’est à dire un cercle. Une des propriétés du cercle est sa largeur constante. Dessi­nons deux tangentes paral­lèles au cercle, et fixons leur distance. Nous commençons à les faire tourner. La courbe (dans notre cas le cercle) est toujours en contact avec les deux lignes.

C’est la défi­ni­tion même d’une courbe fermée avec une largeur constante.

Y a–t–il des autres courbes diffé­rentes du cercle qui ont la largeur constante?

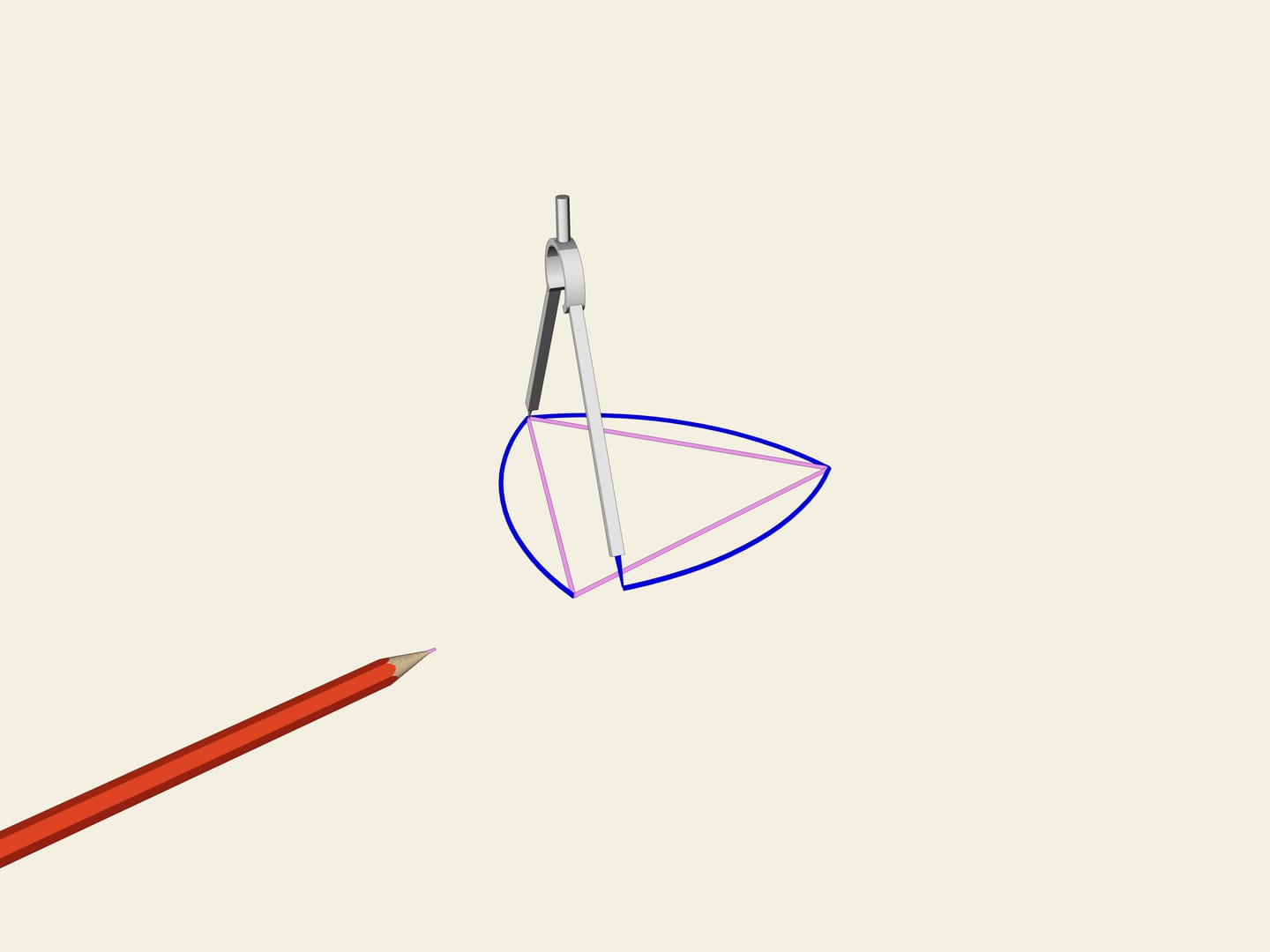
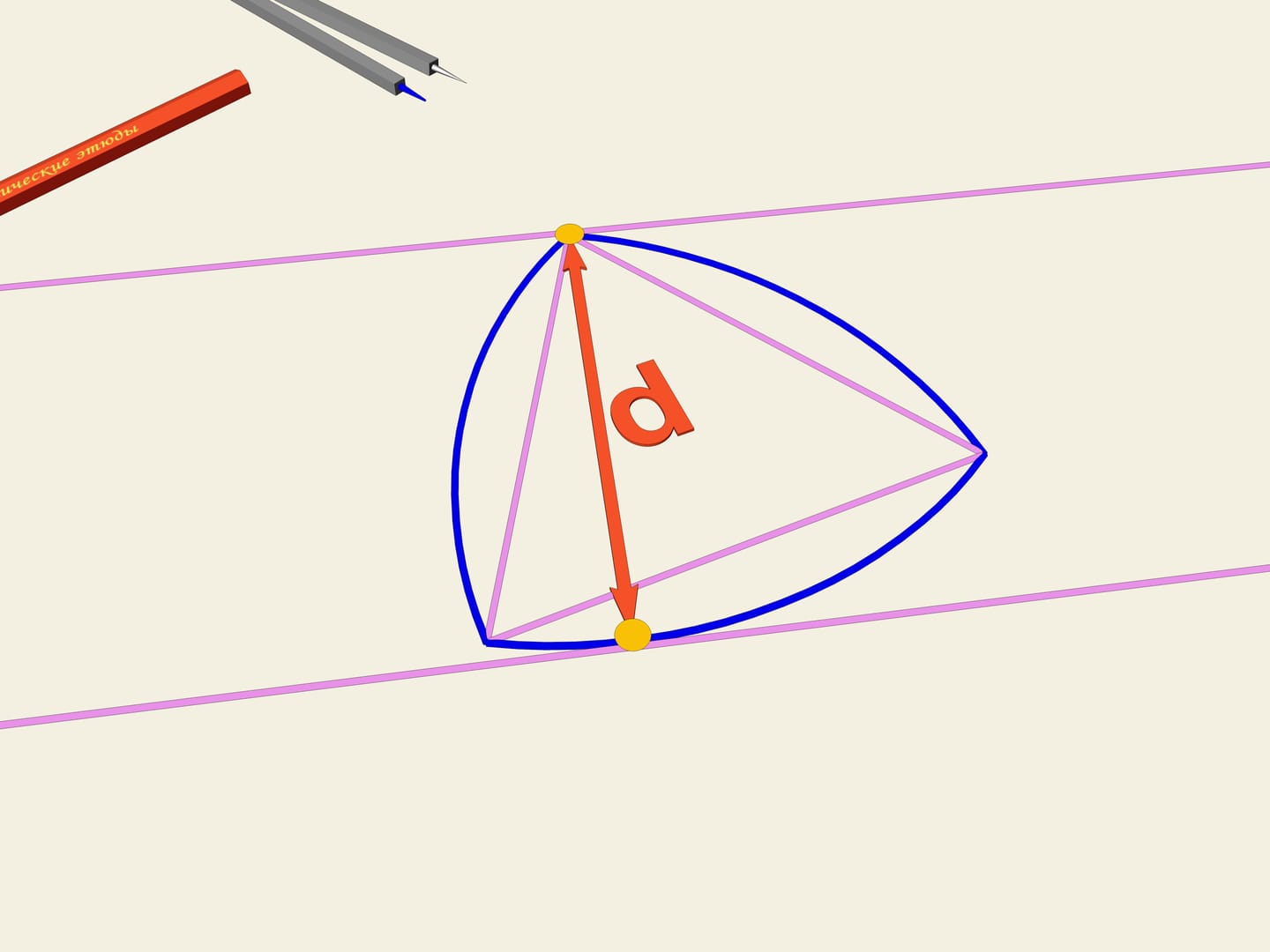
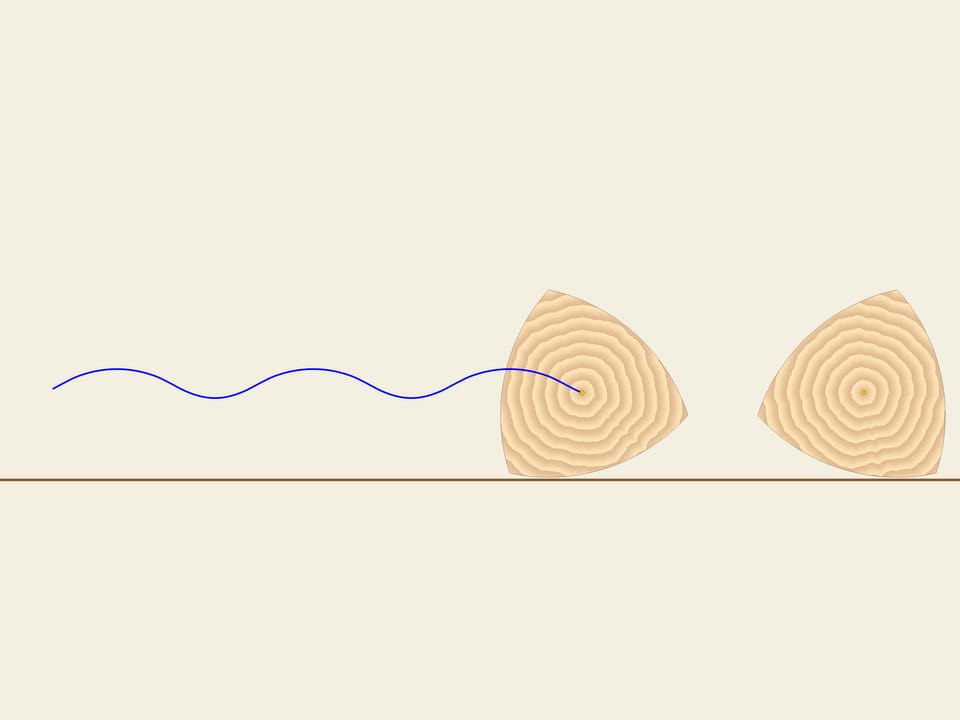
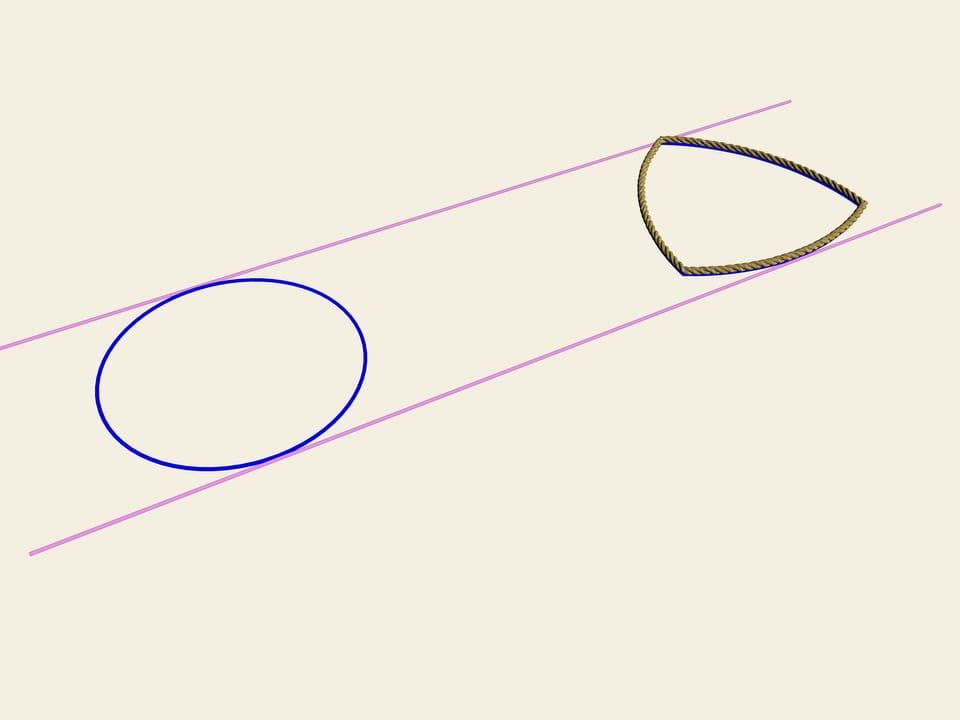
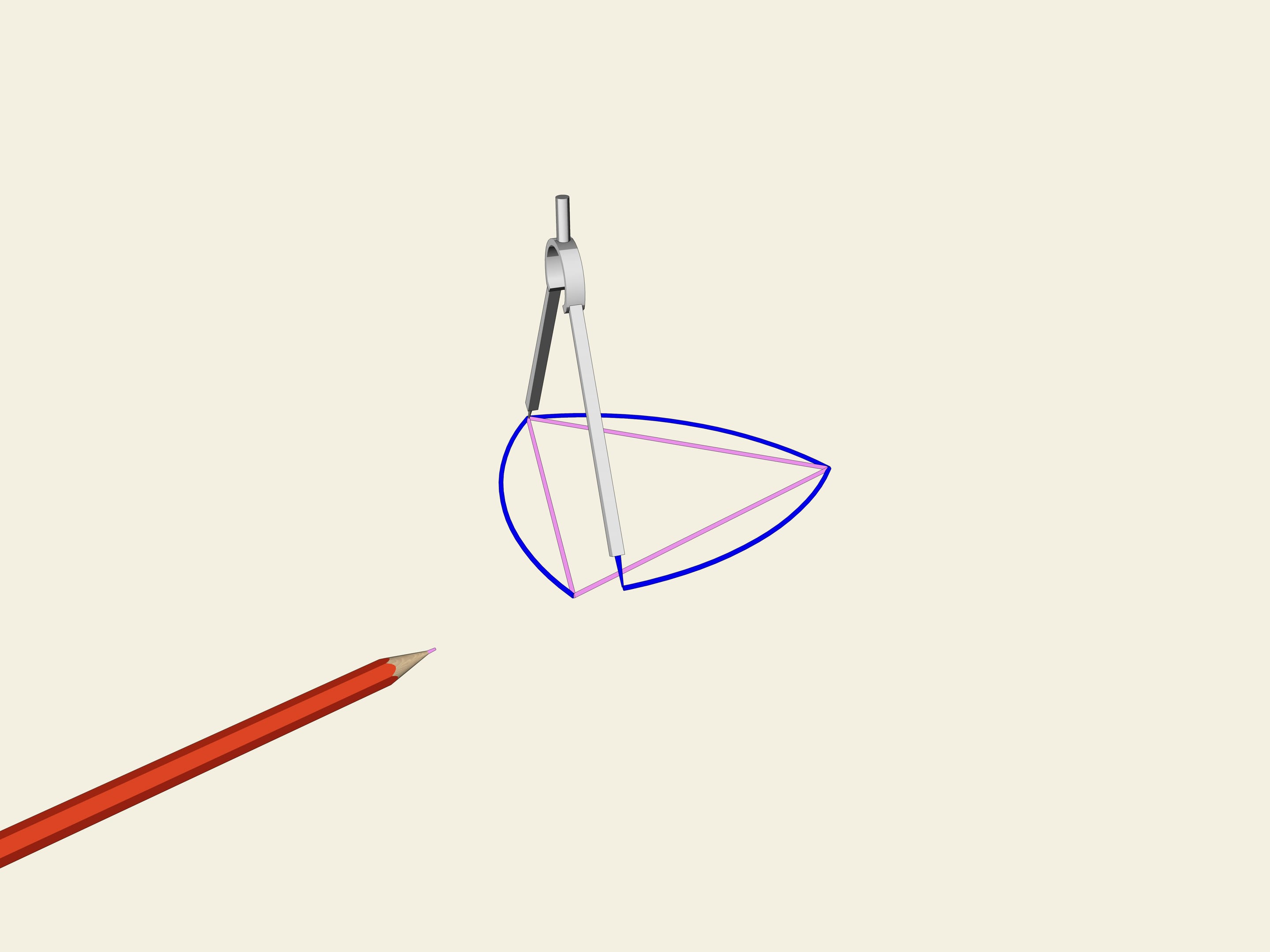
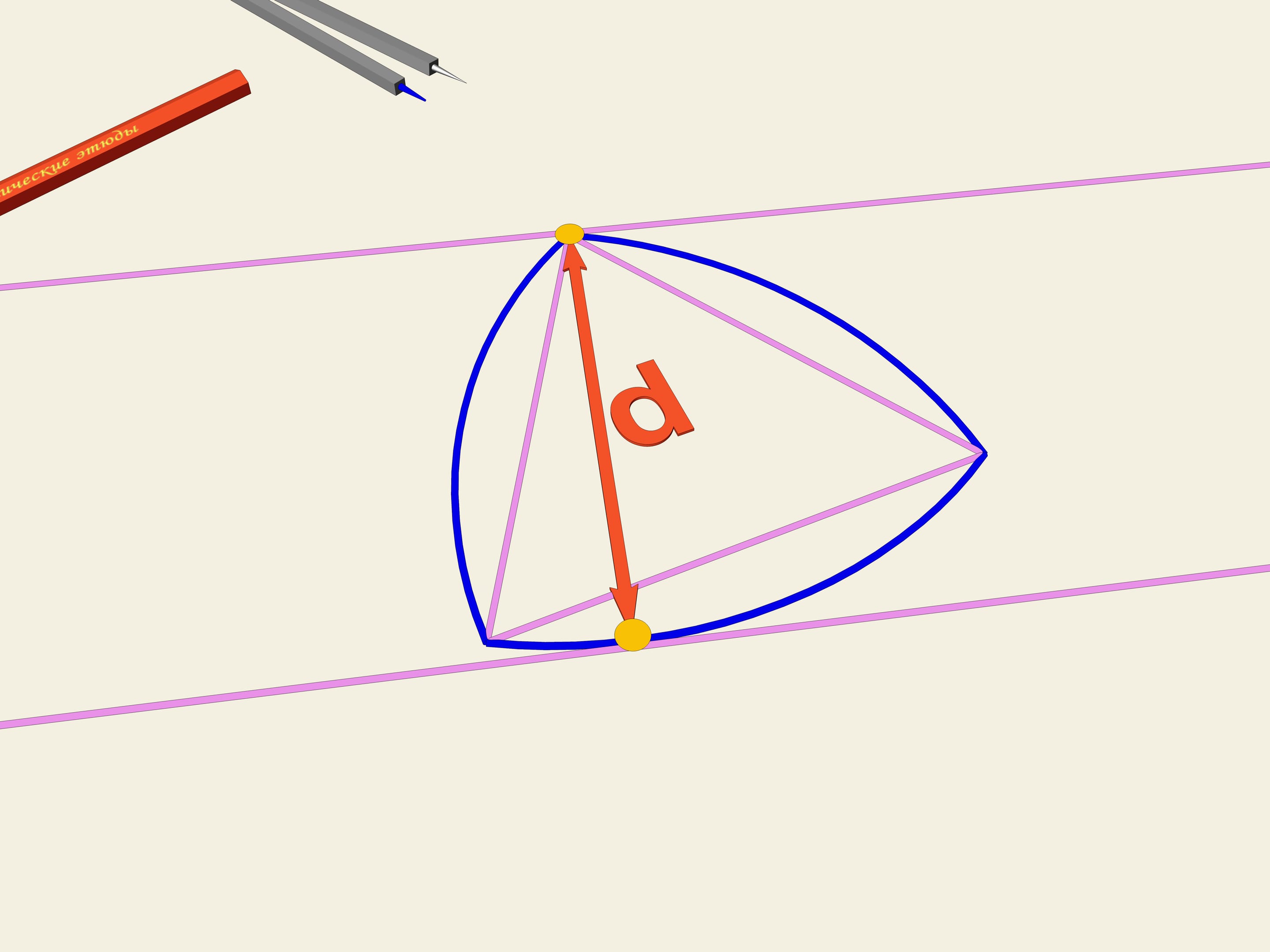
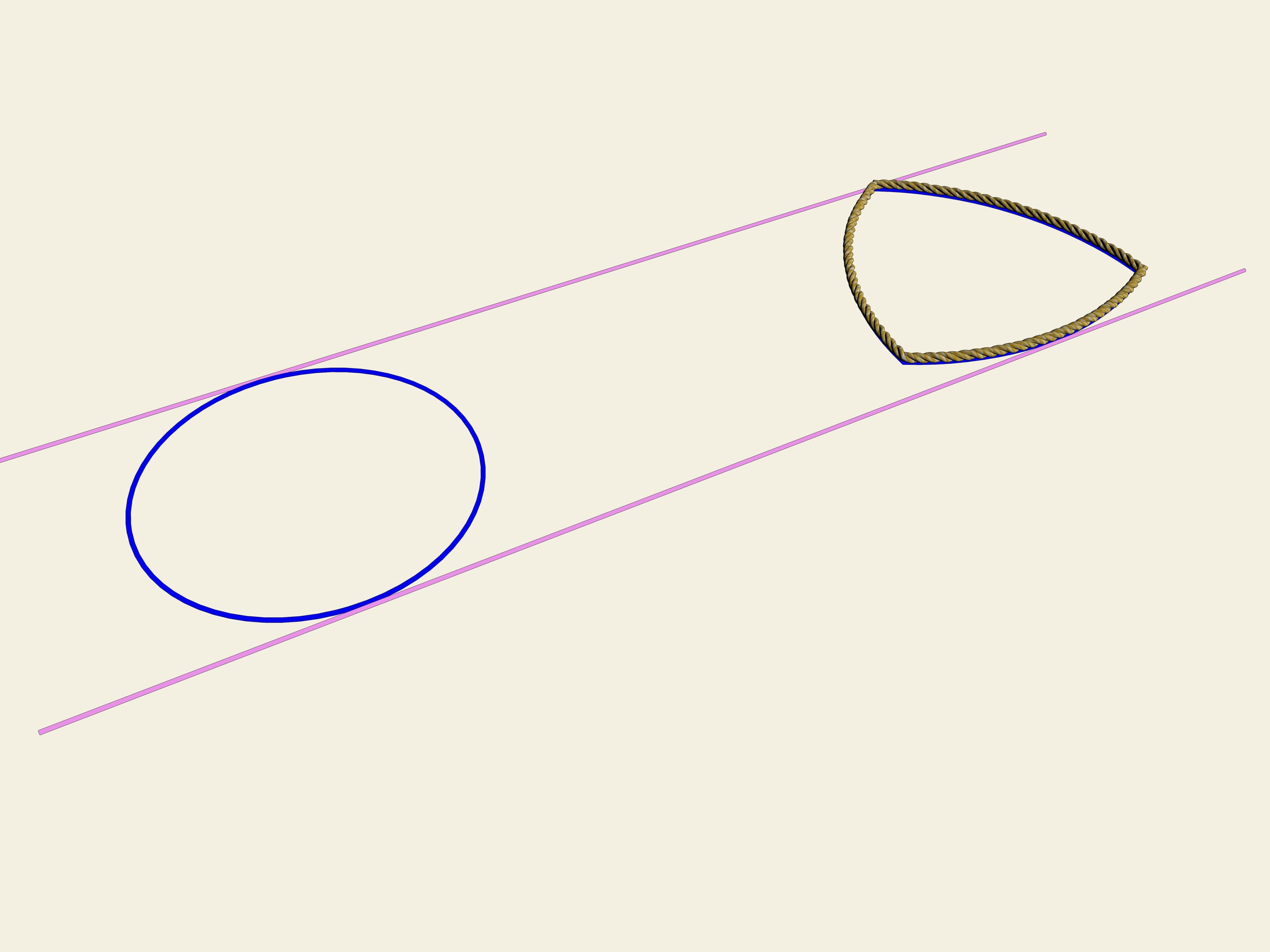
Soit donné un triangle équi­la­téral (avec les côtés égaux). Sur chaque côté on construit un arc de cercle avec un rayon égal à la longueur du côté. La courbe ainsi obtenue s’appelle «triangle de Reuleaux».Il arrive que cette courbe a une largeur constante. Comme dans le cas du cercle, nous prenons deux lignes paral­lèles, fixons la distance entre eux et commençons à les faire tourner. Le triangle de Reuleaux est constam­ment en contact avec les deux barres paral­lèles. En fait, un point de contact est toujours situé dans l’un des sommets du triangle de Reuleaux, tandis que l’autre point, sur la droite paral­lèle, est un point de tangence avec l’arc opposé. Cela signifie que la largeur est toujours égale au rayon du cercle, à savoir la longueur du côté du triangle équi­la­téral initial.

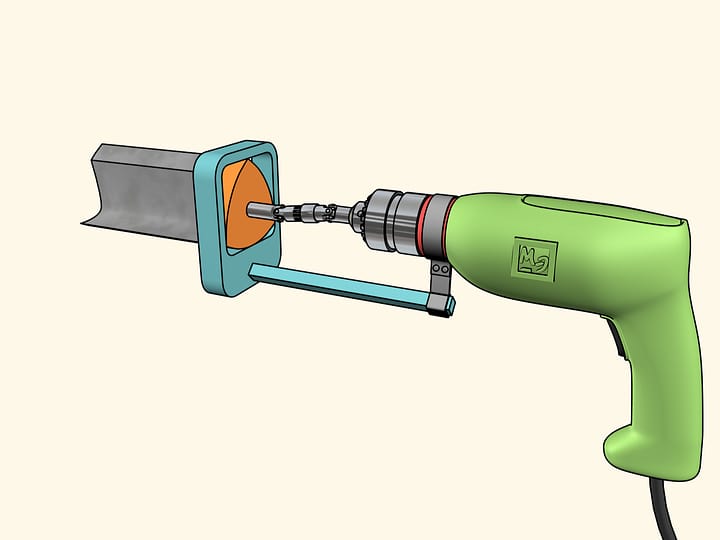
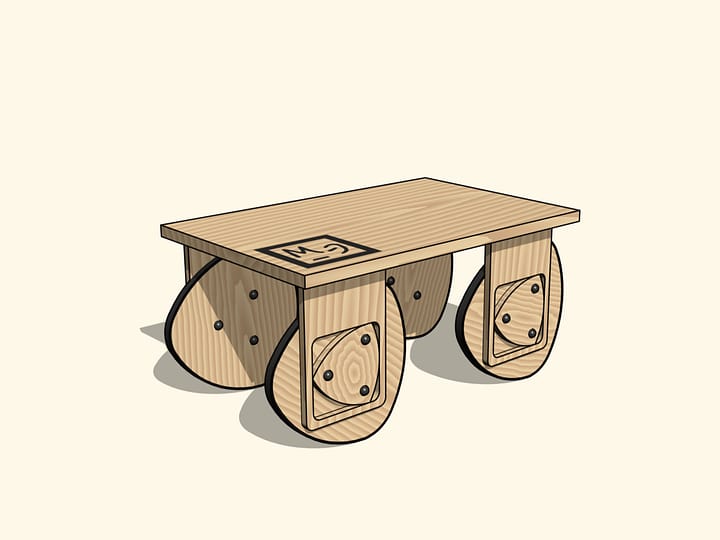
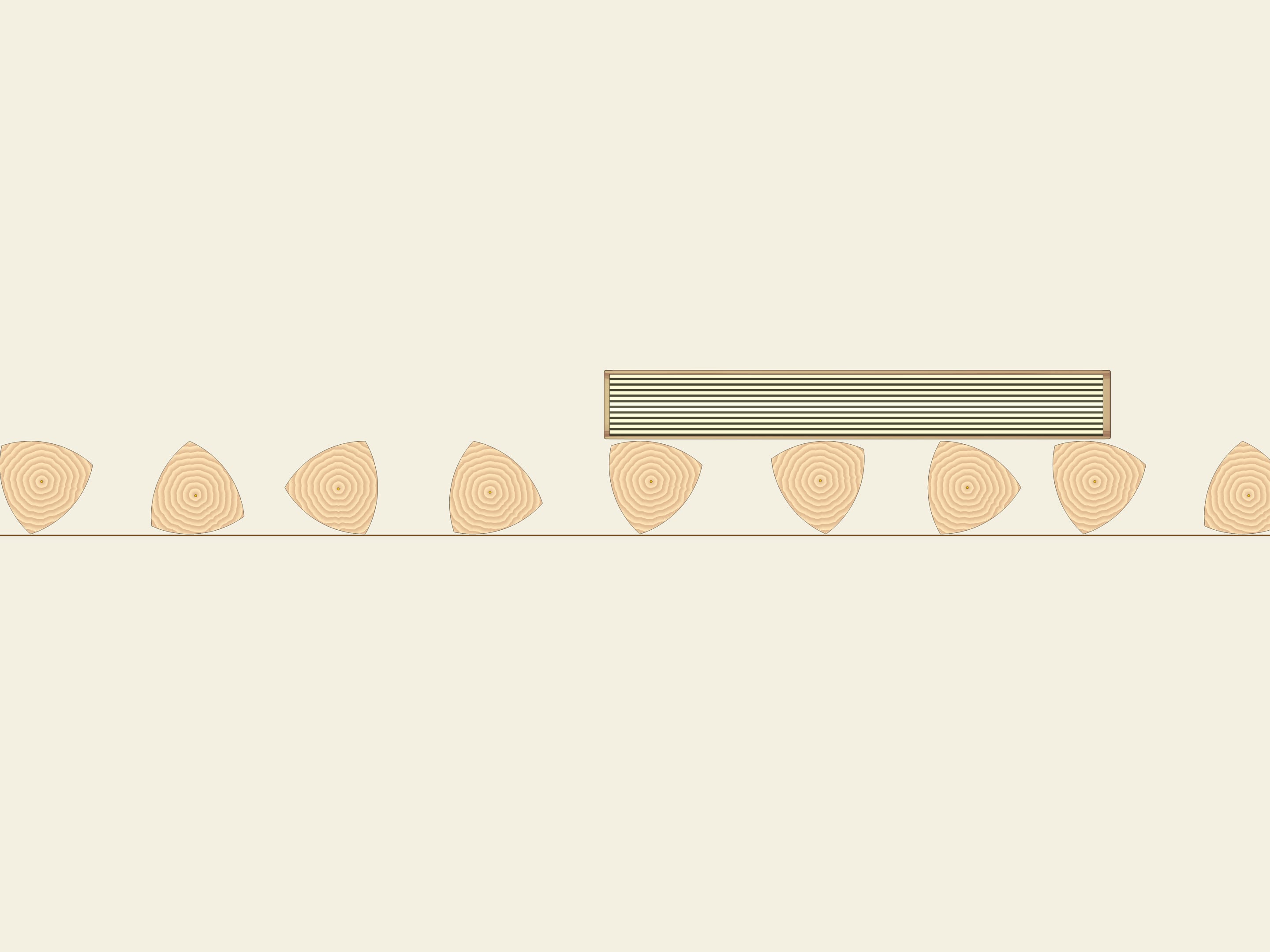
En pratique, la largeur constante de cette courbe implique que si nous construi­sons des rouleaux ayant cette figure comme section, le livre va rouler sur eux, en restant parfai­te­ment hori­zontal.

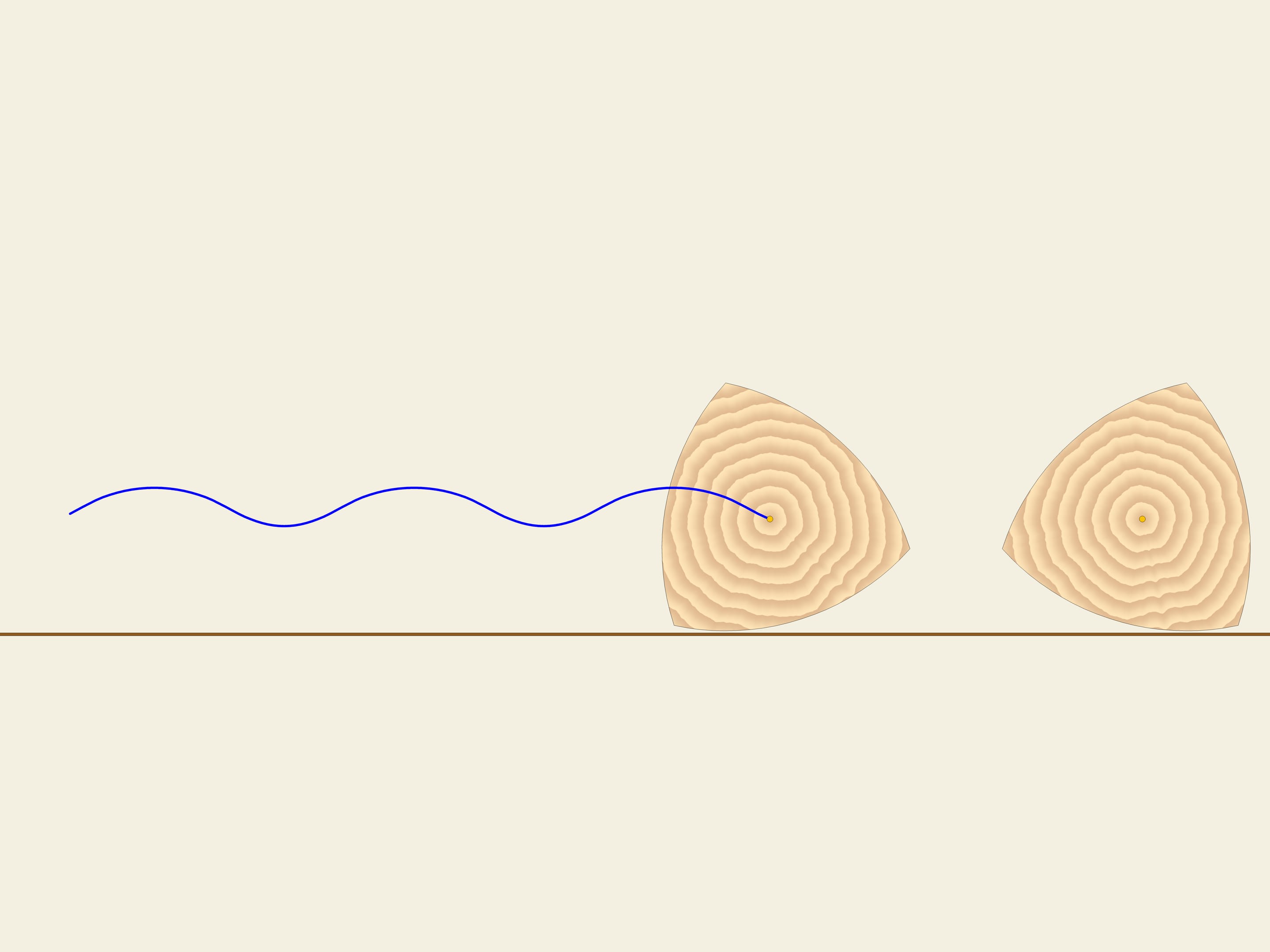
Cepen­dant, on ne pour­rait pas construire un chariot avec des roues à ce profil, car le centre de ces roues décrit une ligne compliquée alors qu’elles roulent sur un terrain plat.

Y a–t–il d’autres courbes de largeur constante? Oui, il y en a, en fait, une infi­nité.

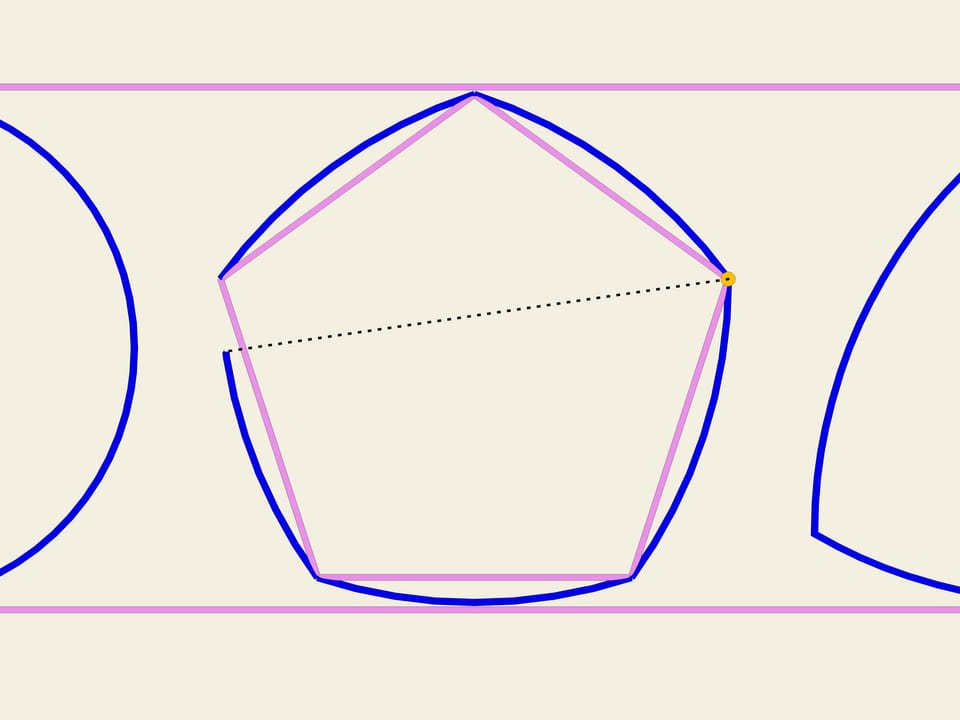
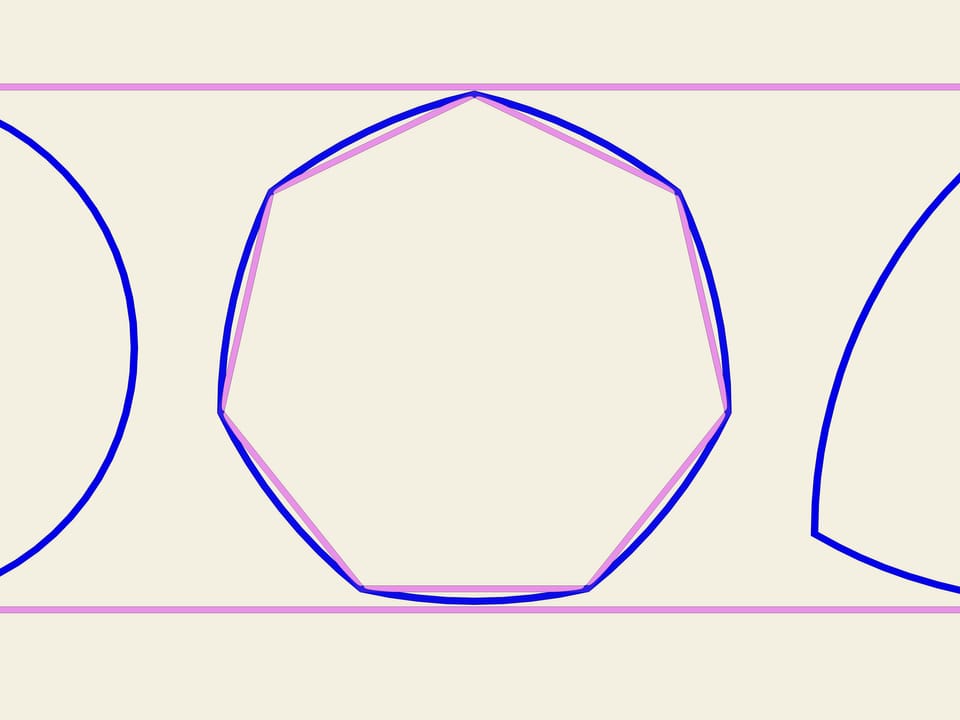
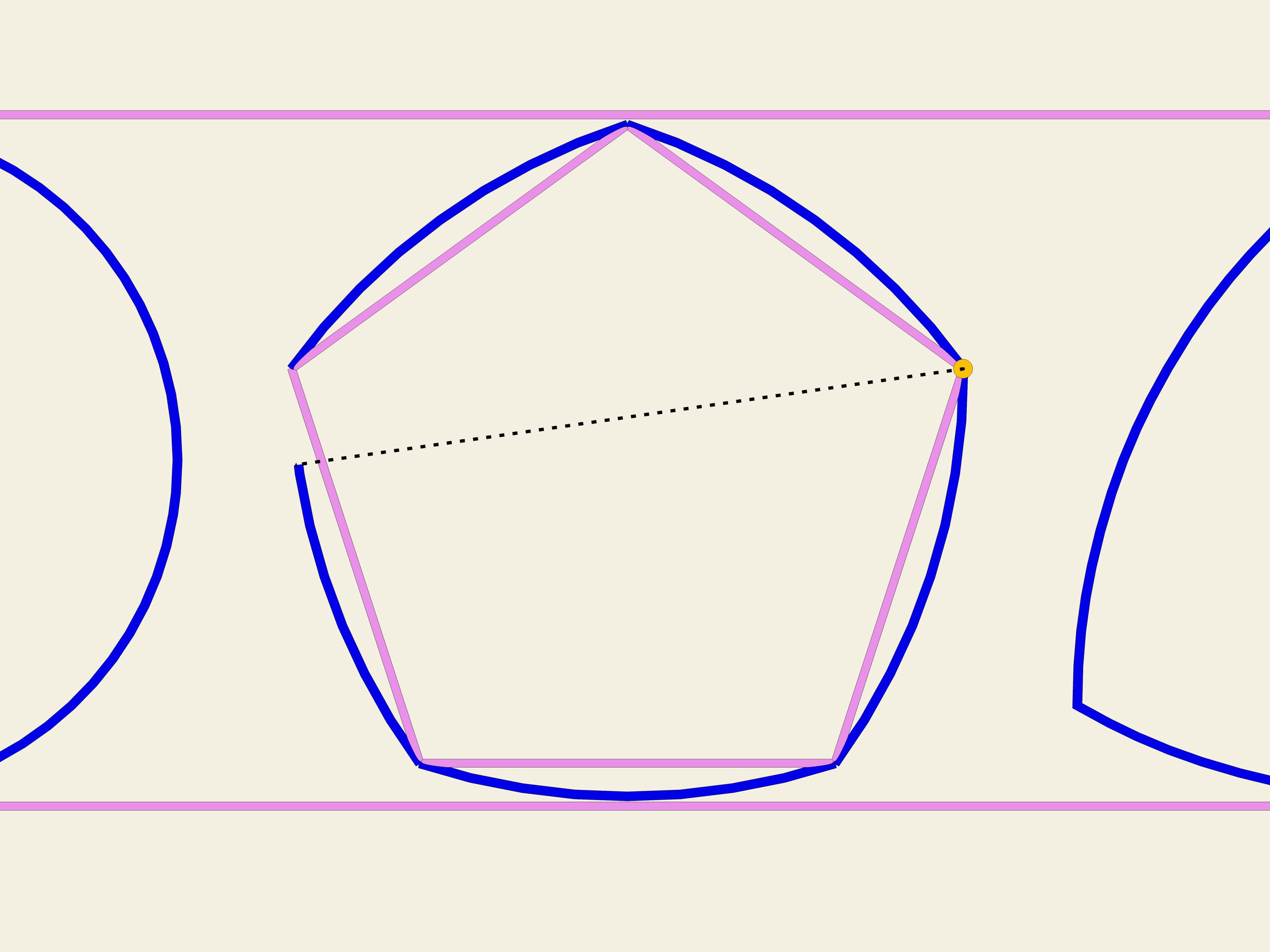
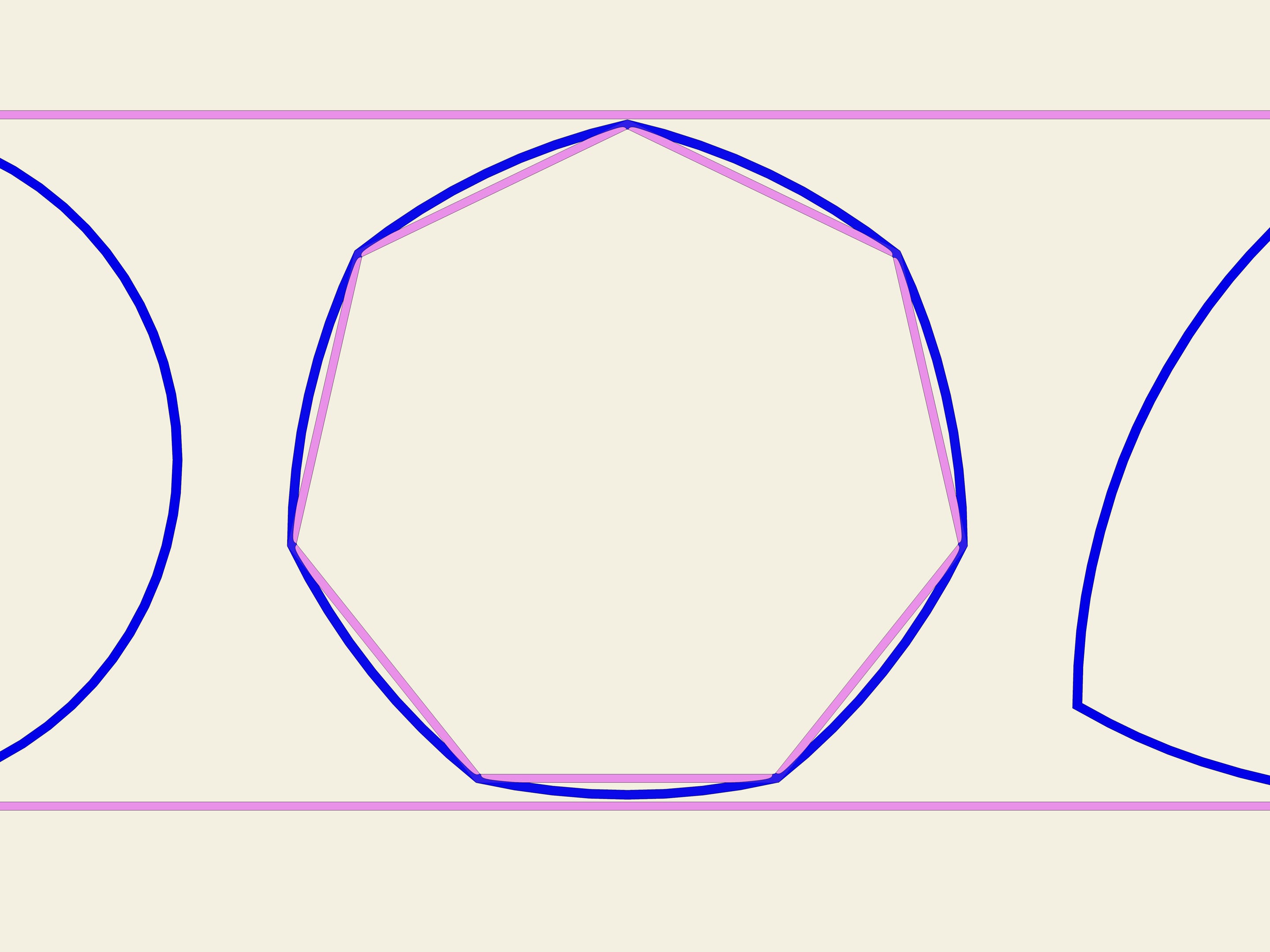
A partir de n’importe quel poly­gone régu­lier avec un nombre impair de côtés, on peut construire une courbe de largeur constante en utili­sant la même procé­dure utilisée pour construire le triangle de Reuleaux. Prenant chaque sommet comme centre, il faut tracer un arc de cercle entre les deux sommets du côté opposé. En Angle­terre, la pièce de 20 pence a la forme d’une courbe de largeur constante, construite sur un hepta­gone.

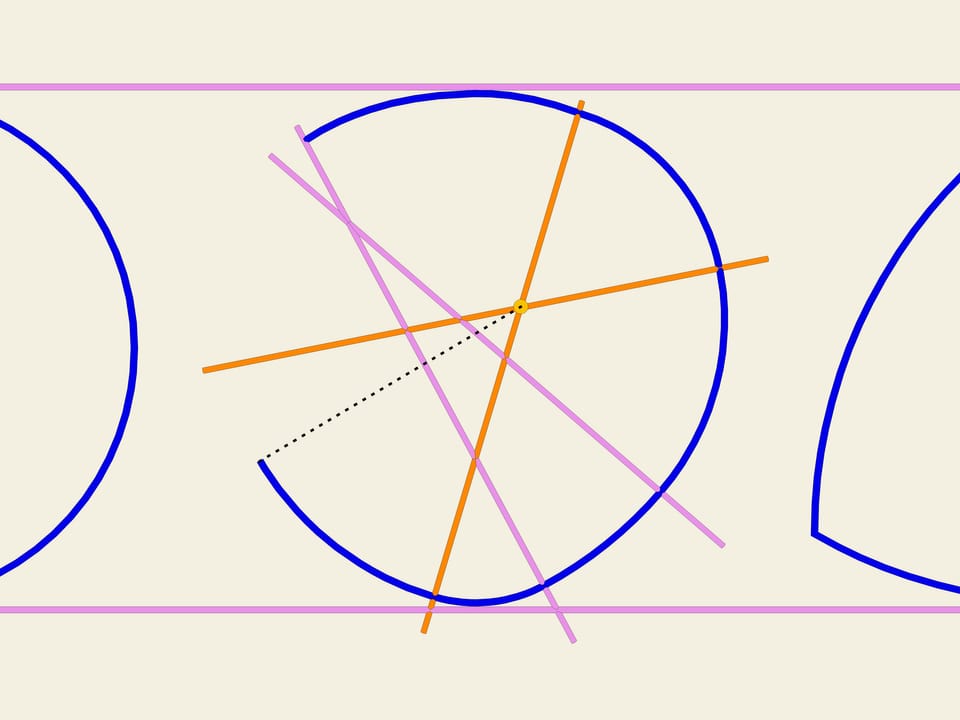
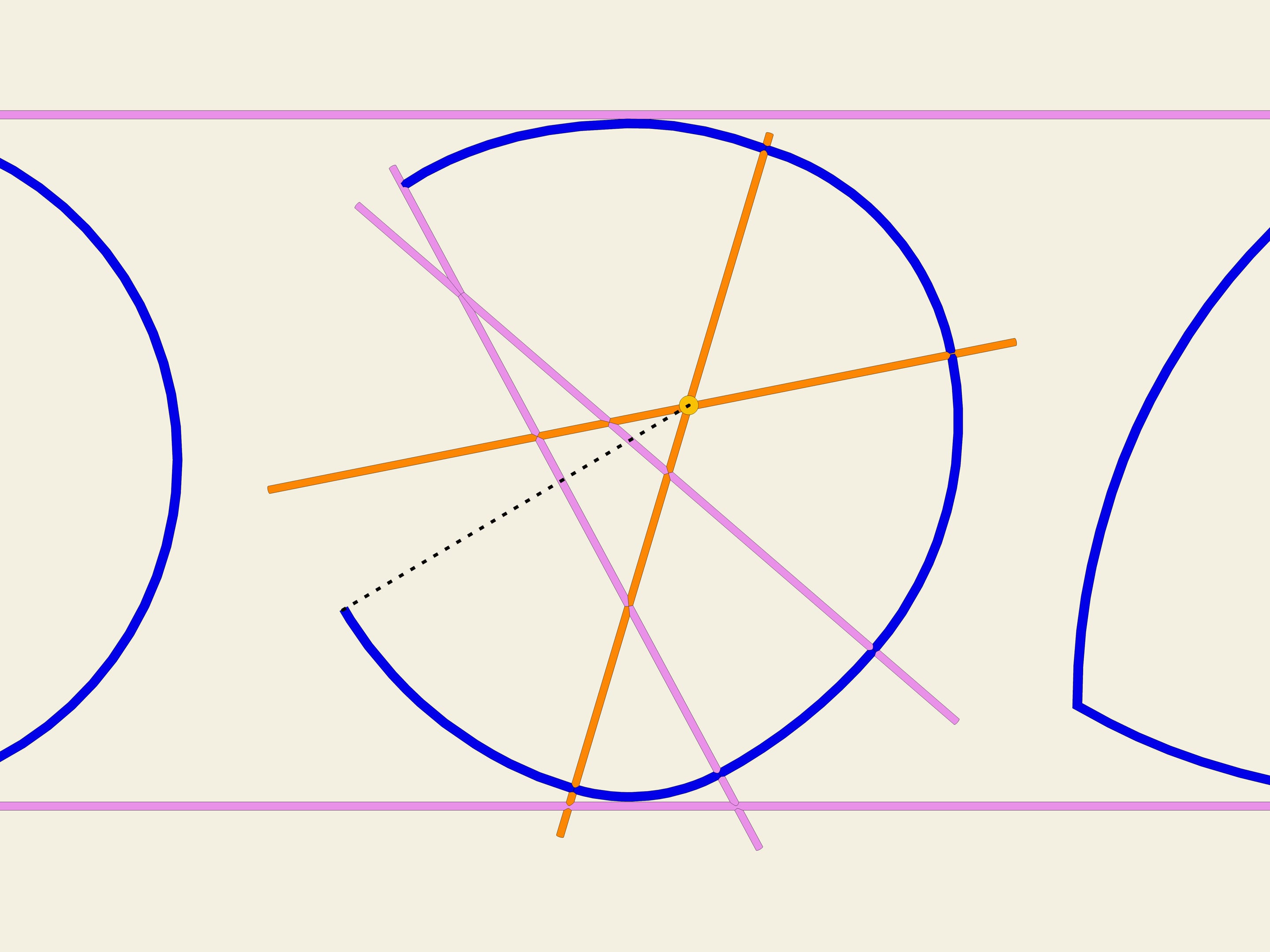
Mais les courbes consi­dé­rées n’épuisent pas la liste de toutes les courbes de largeur constante. Parmi eux, en fait, il ya aussi des courbes non–symé­triques. Consi­dé­rons n droites dans un plan qui se croisent au hasard (n’étant pas paral­lèles les unes aux autres). Elles iden­ti­fient 2n domaines illi­mités. Chacun de ces secteurs a deux côtés qui vont à l’infini. Prenons l’inter­sec­tion de ces deux côtés comme centre, et traçons un arc de cercle, avec un rayon assez grand, entre ces côtés. Puis nous passons au secteur adja­cent et traçons un arc d’une façon pareille, cette fois son rayon est déter­miné par le fait qu’il doit prolonger conti­nuel­le­ment l’arc précé­dent. Eten­dons ce processus à tous les secteurs. La courbe ainsi obtenue, consti­tuée d’arcs de cercles, est une courbe fermée de largeur constante. Démon­trez–le!

Toutes les courbes d’une largeur donnée ont la même longueur. Le cercle et le triangle de Reuleaux avec la même largeur égale­ment partagent la propriété d’être des courbes extré­males parmi les courbes de la même largeur: le cercle entoure la surface d’aire maxi­male, et le triangle de Reuleaux la surface d’aire mini­male.

Le triangle de Reuleaux n’est pas seule­ment inté­res­sant pour les mathé­ma­ti­ciens, cette figure a des appli­ca­tions surpre­nantes en méca­nique.

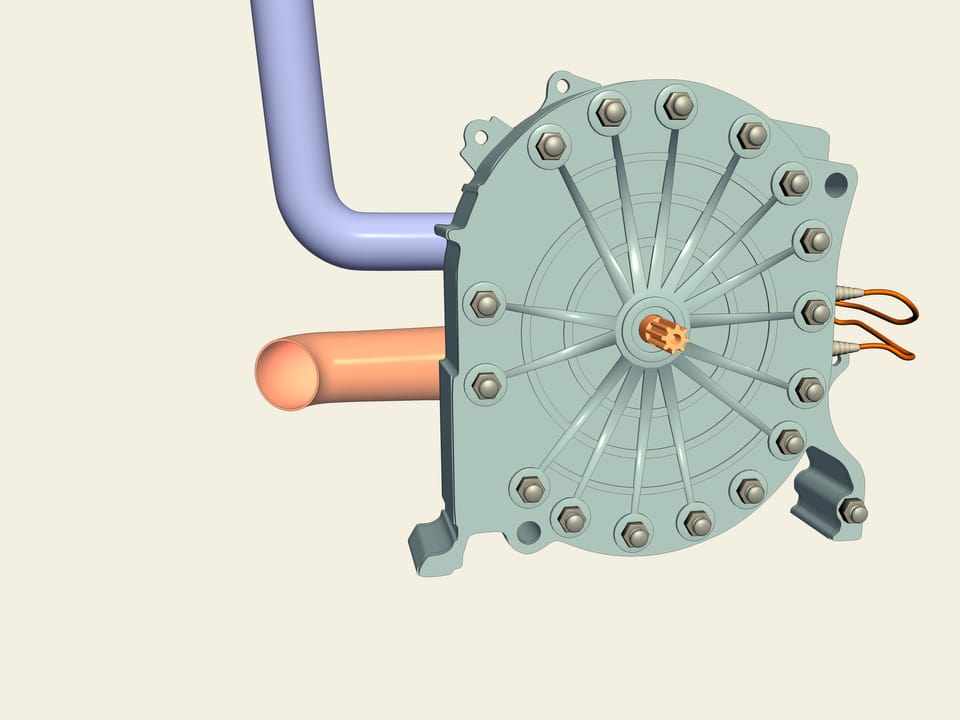
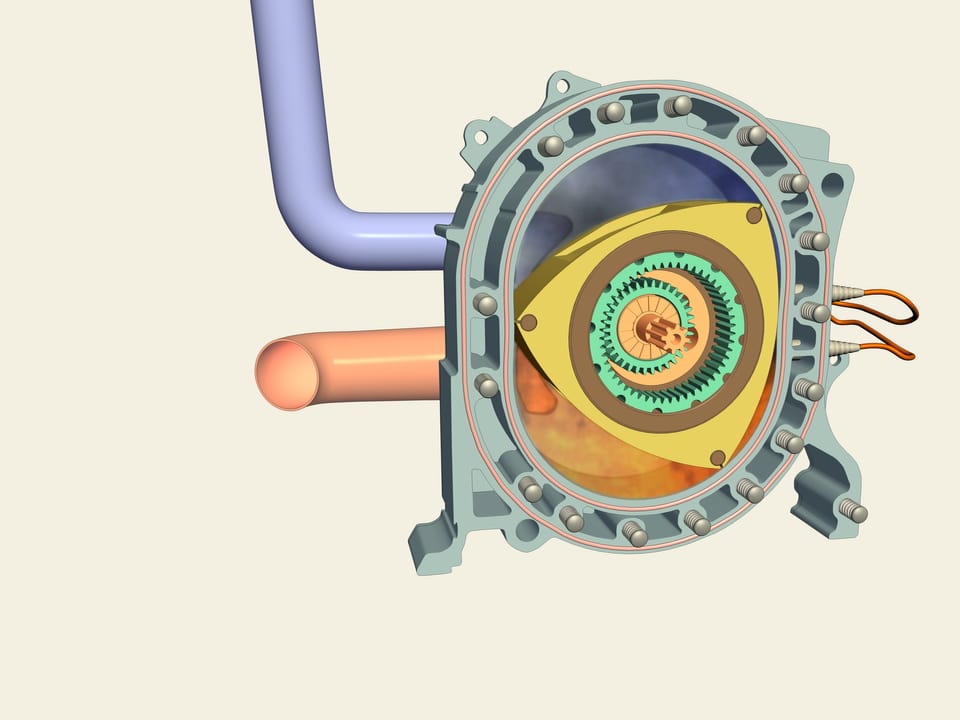
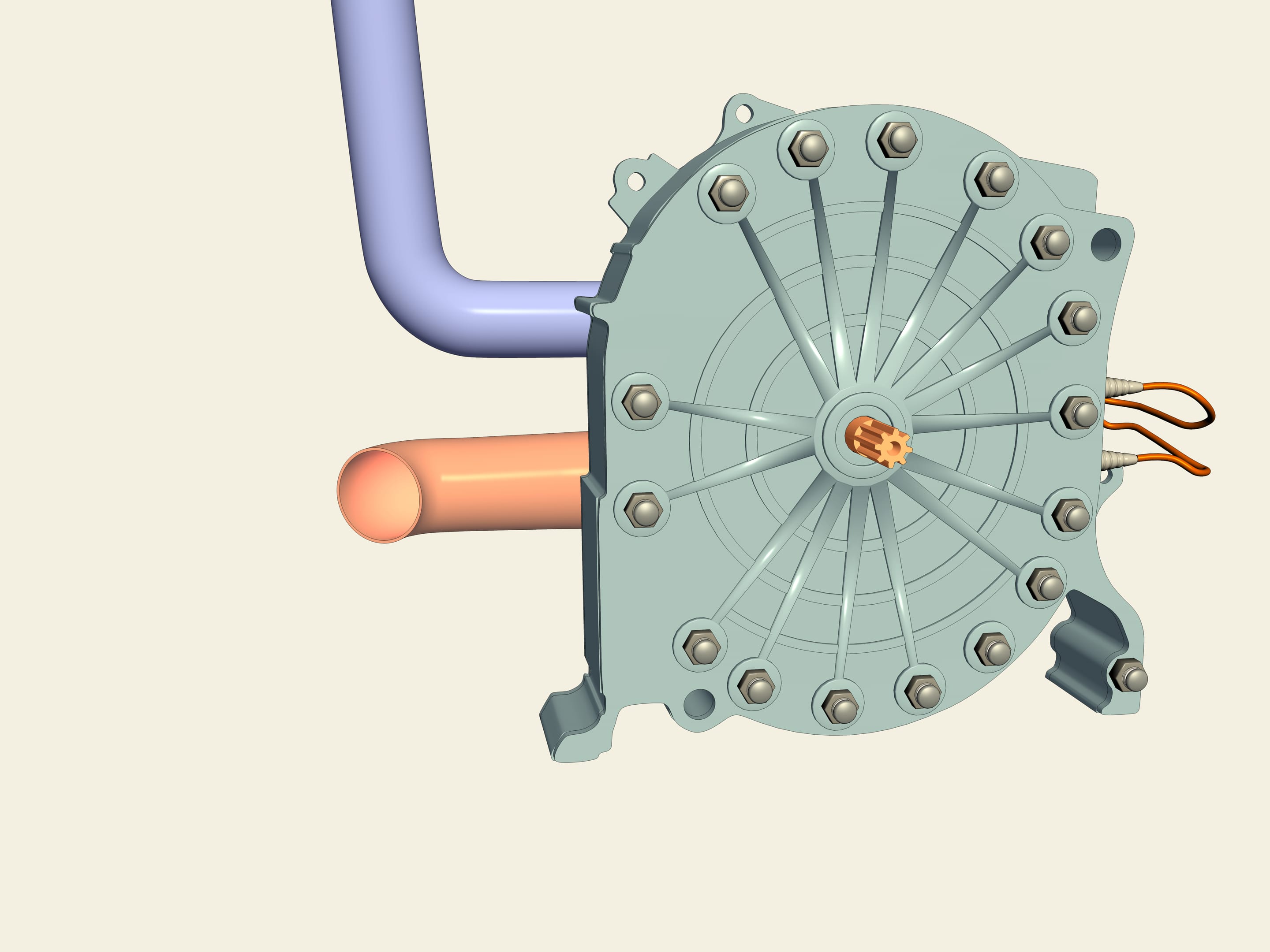
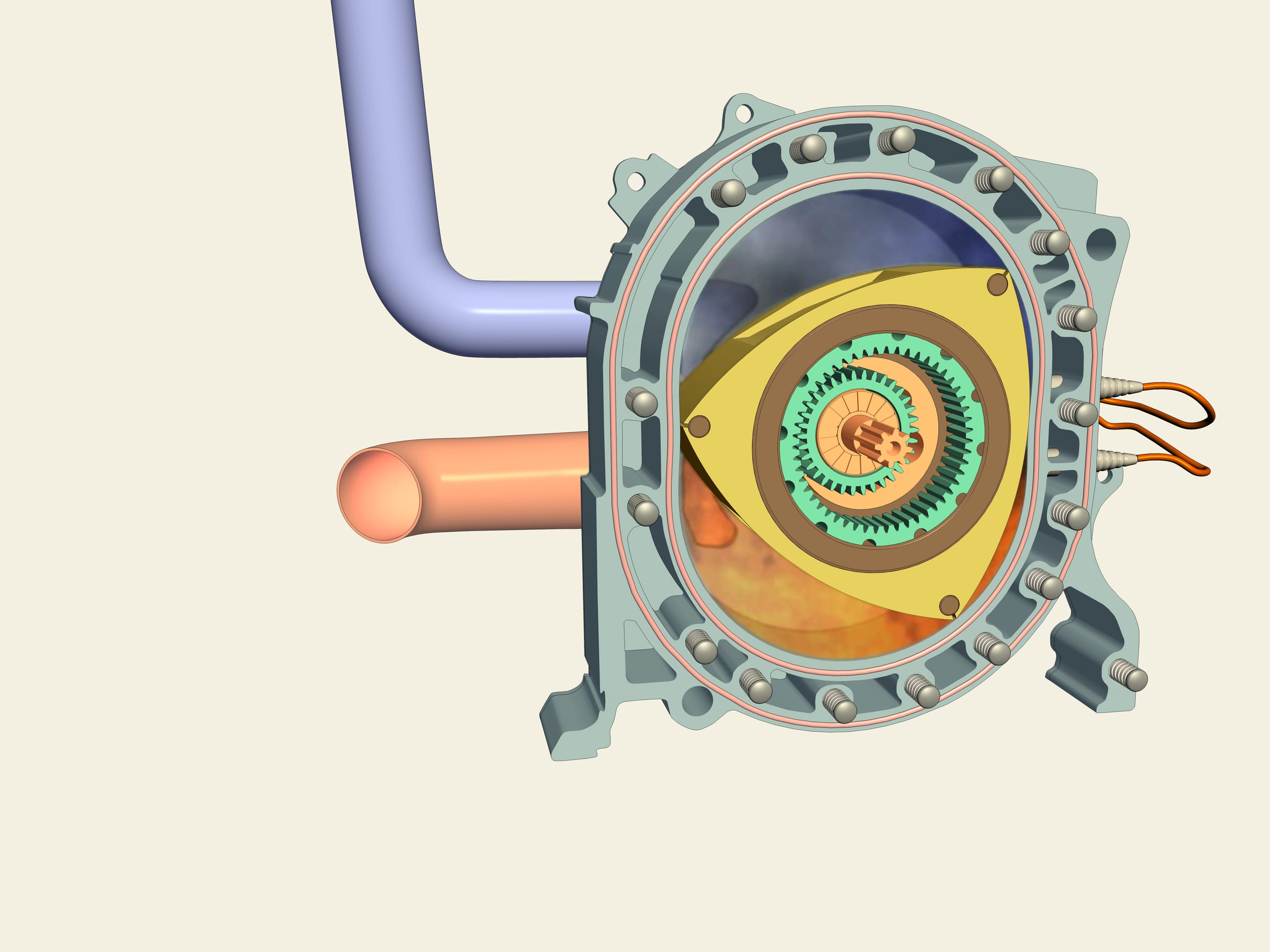
Observez: il s’agit d’une “Mazda RX–7”. Contrai­re­ment à la majo­rité des voitures, en lui (comme dans le RX–8) il y a un moteur rotatif Wankel. Comment est il fait? Le rotor a la forme d’un triangle de Reuleaux! Entre lui et les parois trois chambres se forment, dont chacune est à son tour une chambre de combus­tion. L’essence (en bleue), une fois intro­duite, en raison du mouve­ment du rotor est comprimé, ensuite, à cause de l’écla­te­ment, le rotor tourne. Le moteur rotatif est exempt de certains défauts de la contre­partie à piston: la rota­tion est direc­te­ment trans­mise à l’axe et il n’est donc pas néces­saire d’utiliser l’arbre de trans­mis­sion.

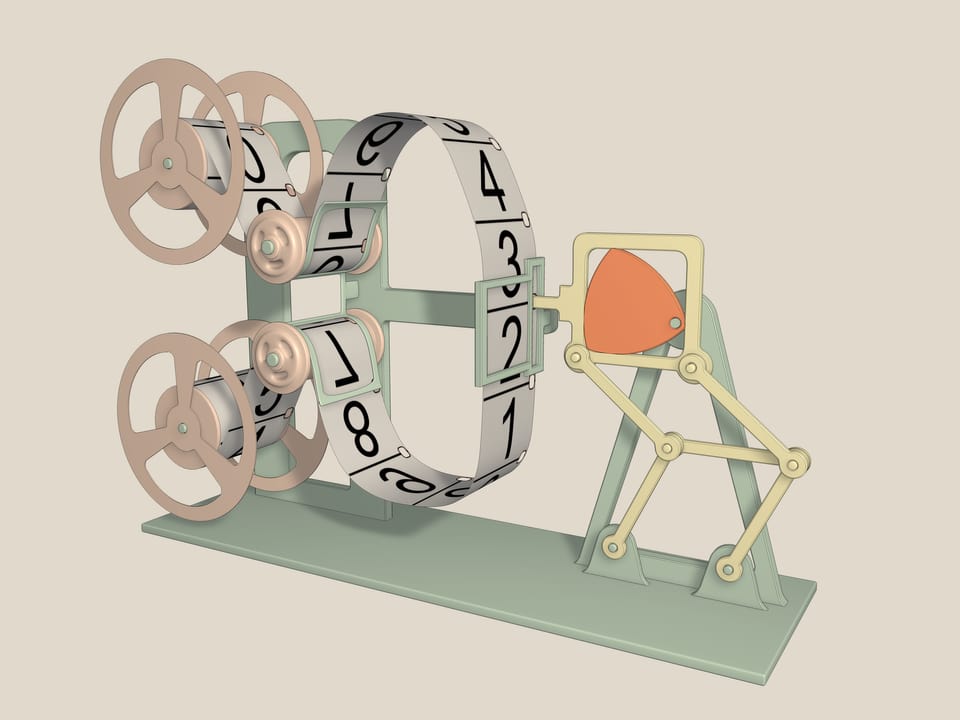
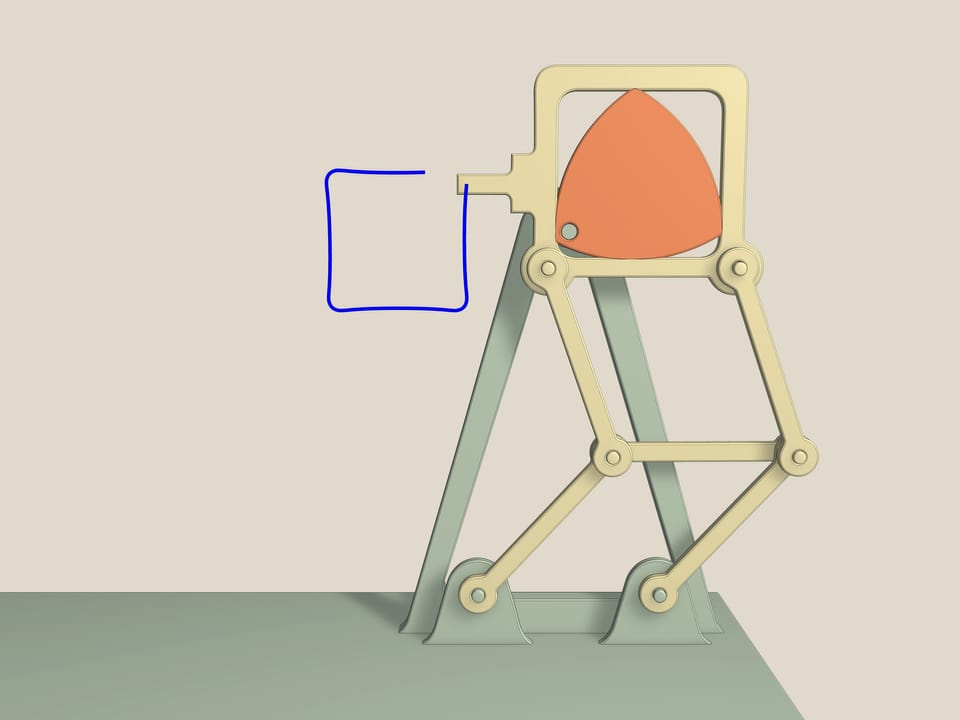
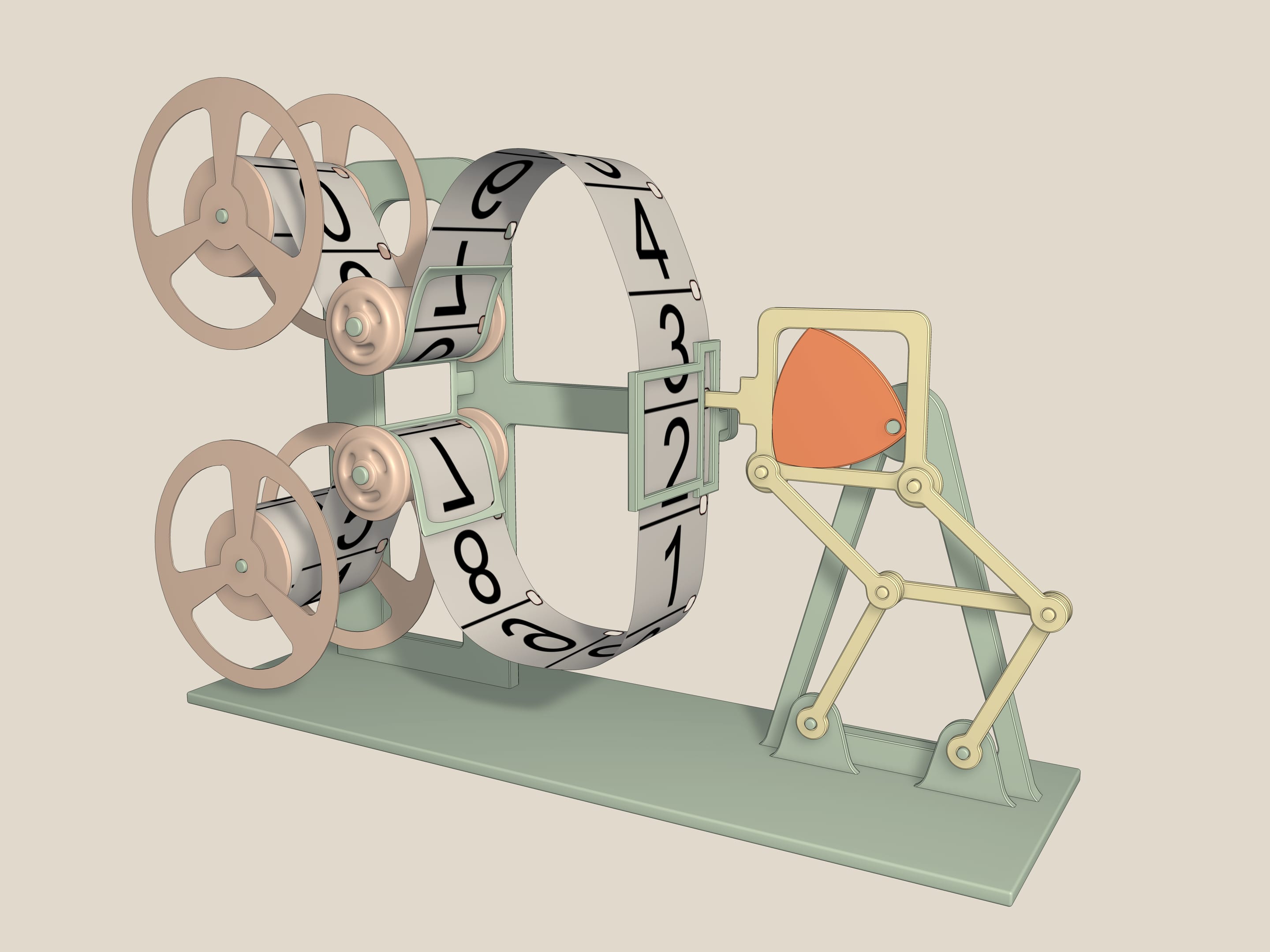
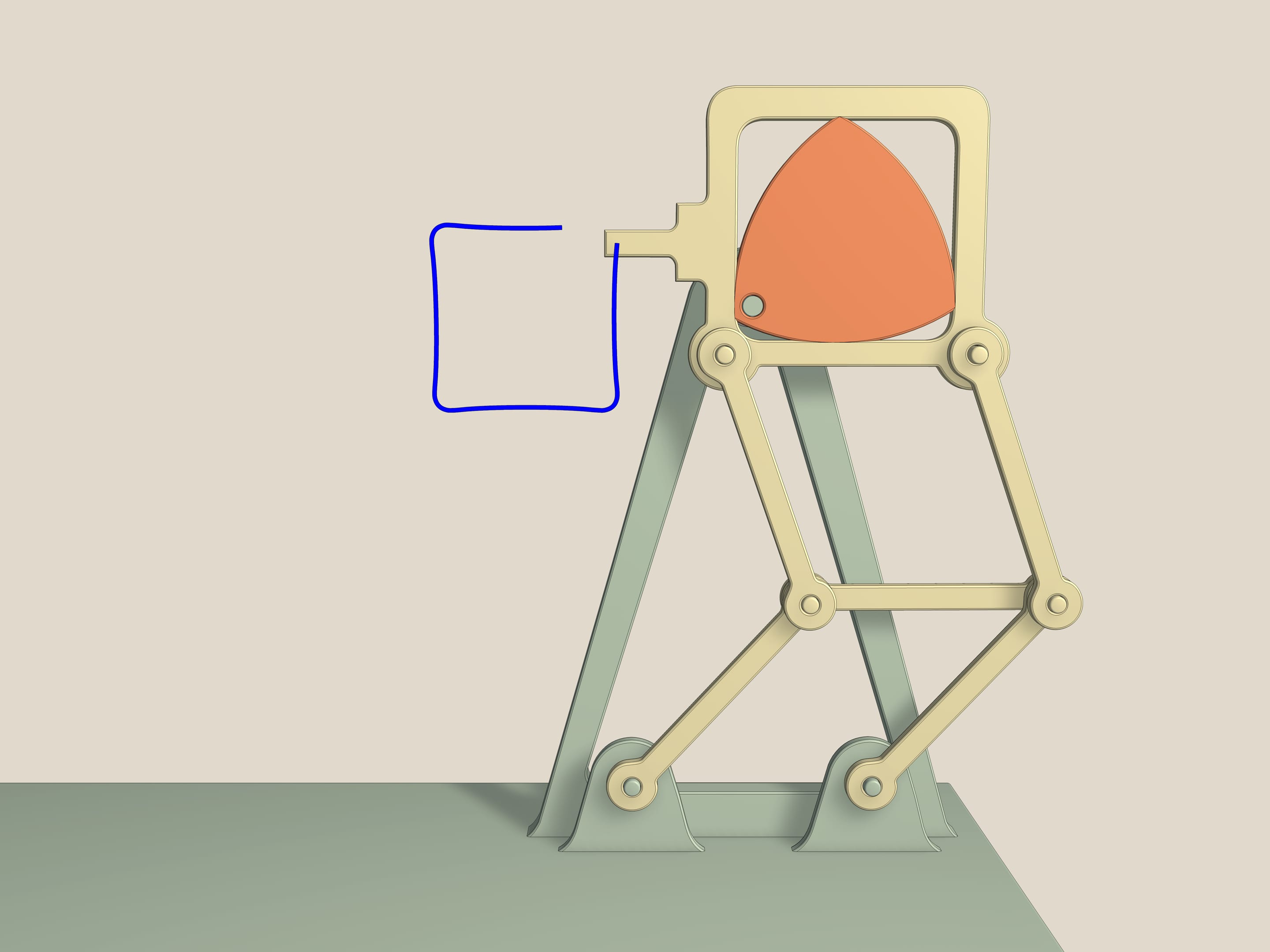
Celui–ci c’est un méca­nisme de projec­tion de films. Le moteur d’un appa­reil pareil, en fait, génère une rota­tion continue autour d’un axe, mais afin d’avoir des images nettes sur l’écran, chaque image doit rester un moment immo­bile, tandis que la tran­si­tion d’un cadre à l’autre doit se dérouler dans un temps beau­coup plus court. Tout cela 18 fois par seconde. Ce problème est effec­ti­ve­ment résolu simple­ment par un méca­nisme qui est basé sur le triangle de Reuleaux, inscrite dans un carré, et un double paral­lé­lo­gramme, ce qui empêche au carré de s’incliner. En fait, comme les longueurs des côtés opposés sont égaux, l’élément central pendant les mouve­ments reste paral­lèle à la base et le côté du carré reste toujours paral­lèle à l’élément central. Plus l’axe de rota­tion est proche d’un sommet du triangle de Reuleaux, plus la dent du méca­nisme décrit une figure qui ressemble à un carré.

Nous avons donc appris des appli­ca­tions inté­res­santes de purs objets mathé­ma­tiques.