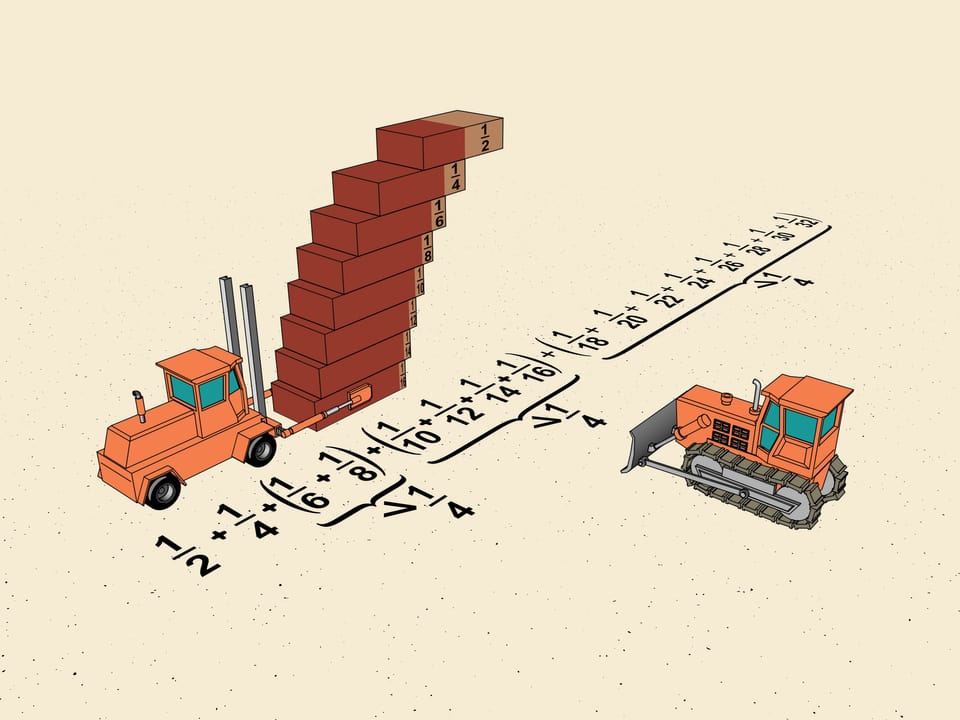
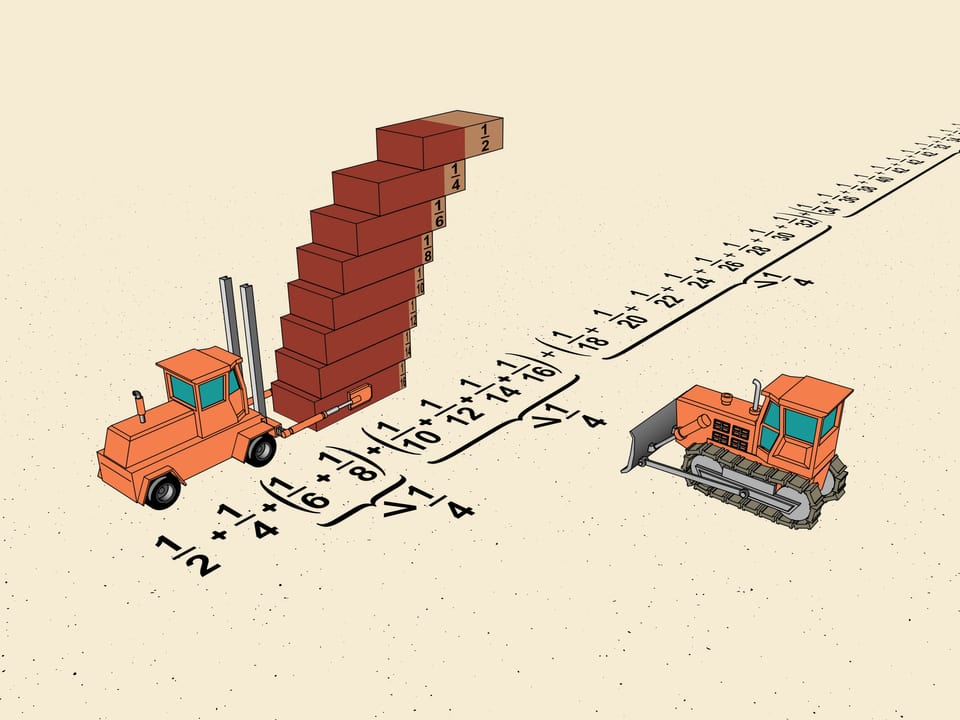
Quelle est la position limite où il faut mettre une brique sur l'autre, afin qu'il ne tombe? Évidemment, au milieu de la première brique. En fait, le centre de gravité d'une brique est dans son milieu, de sorte qu’on peut la poser exactement sur une autre, et après la déplacer de la moitié de sa longueur.
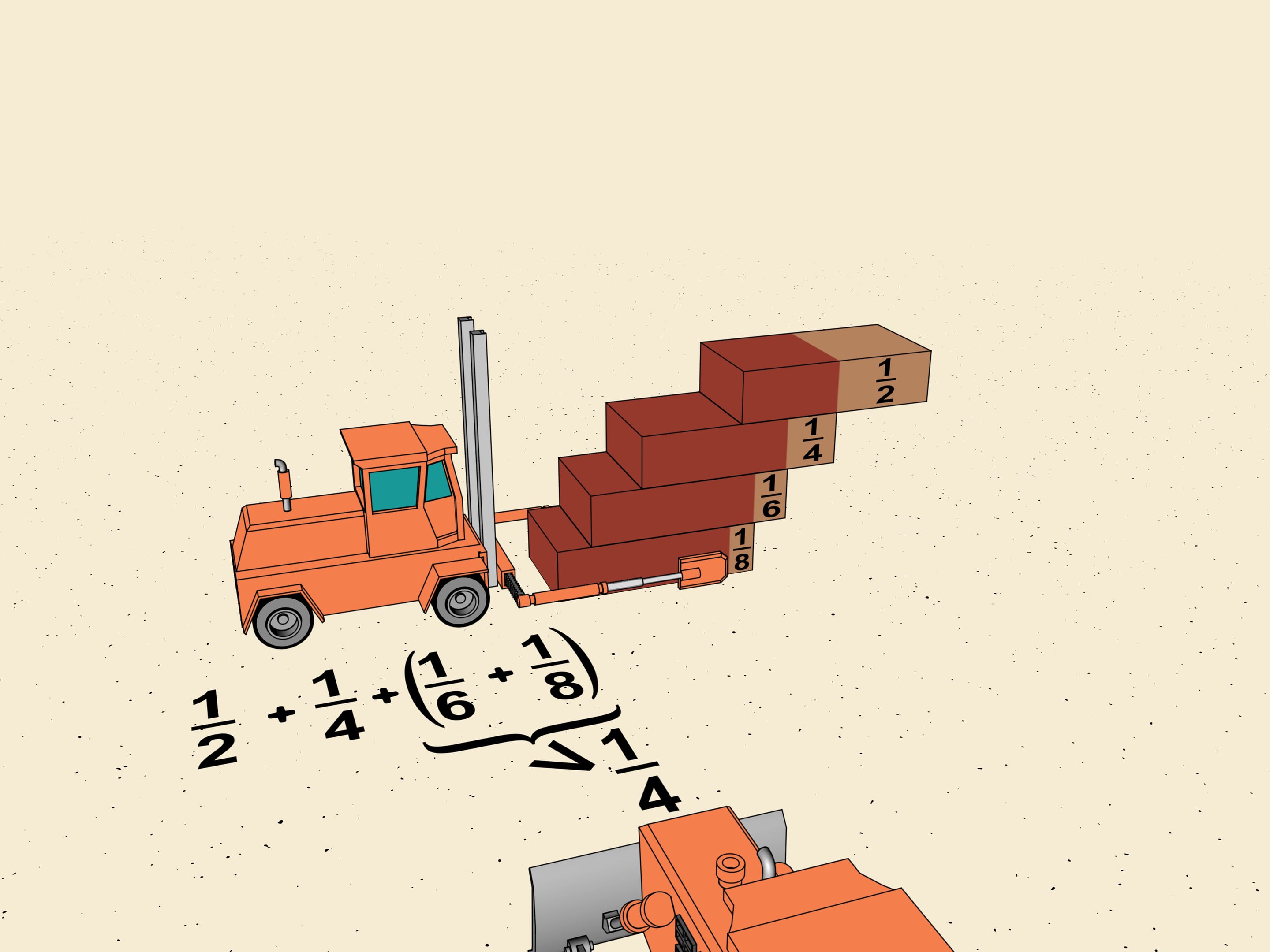
Mais quelle est la position limite où il faut mettre ce système de deux briques sur une autre brique? Il n'est pas difficile de calculer que le centre de gravité de notre construction de deux briques est situé à distance de 1/4 de la longueur d'une brique du bord de la brique de dessous. En fait, le centre de gravité du système est situé à mi chemin entre les deux bords, c'est à dire à un quatrième à partir du bord de la brique inférieure, et doit se projeter sur le bord de la brique de dessous.
Le tracteur porte encore une brique. Comme nous l'avons vu, les deux premières peuvent être déplacées d'un quart de leur longueur pare rapport à celle-ci.
Le papillon est une créature légère, et les conducteurs des machines s’amusent à jouer avec elle. Mais voila elle se pose sur les briques. Si elle atterrit sur un point qui se projette sur le brique plus en bas, la construction va tenir. Mais la voila voler encore et se poser un peu plus à droite, et l’escalier perd son équilibre. Le soulevateur doit se dépêcher pour soutenir la construction afin qu'elle ne s’écroule pas. Cela nous montre une fois de plus que les déplacements de $1/2$ et $1/4$ de la longueur sont les maximum autorisés, lorsque l’escalier est construit sans ciment, et il ne se tient que pour la gravité des briques.
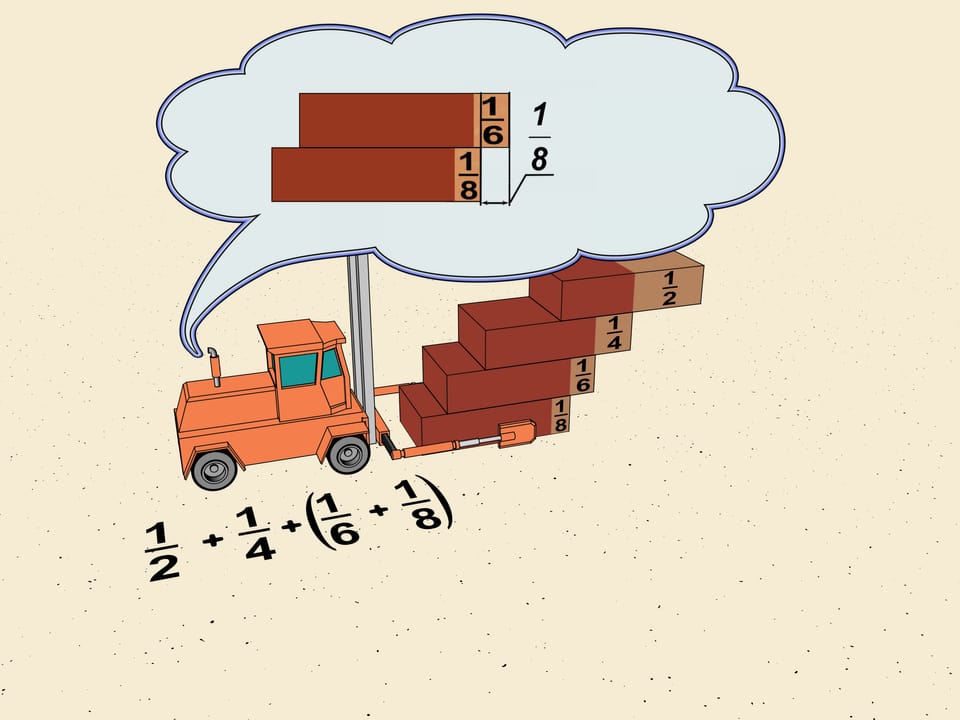
Mais où est le centre de gravité du système de trois briques? Le centre de gravité des deux premières briques se projette sur le bord de la brique-dessous, qui a son centre de gravité dans le milieu. Mais maintenant, les poids correspondants à ces deux centres ne sont pas les mêmes: nous avons à droite la masse de deux briques, et è gauche celle d’une seule. En conséquence, la ligne verticale passant par le centre de gravité du système de trois briques divise la distance entre le centre et le bord de la brique-dessous, calculée à partir du centre, en deux parties qui sont dans le rapport 2:1. Cette ligne est donc loin du bord de $1/6$ de la longueur d'une brique.
De la même façon nous pouvons calculer que, si l’on veut bâtir un escalier sans utiliser le ciment, on peut le faire en déplaçant à chaque fois le système de $n$ exactement de $1/2n$ la longueur d'une brique par rapport au bord de la brique plus en bas. Nous allons faire ainsi, nous déplaçant du maximum autorisé à l'horizontale à chaque étape.
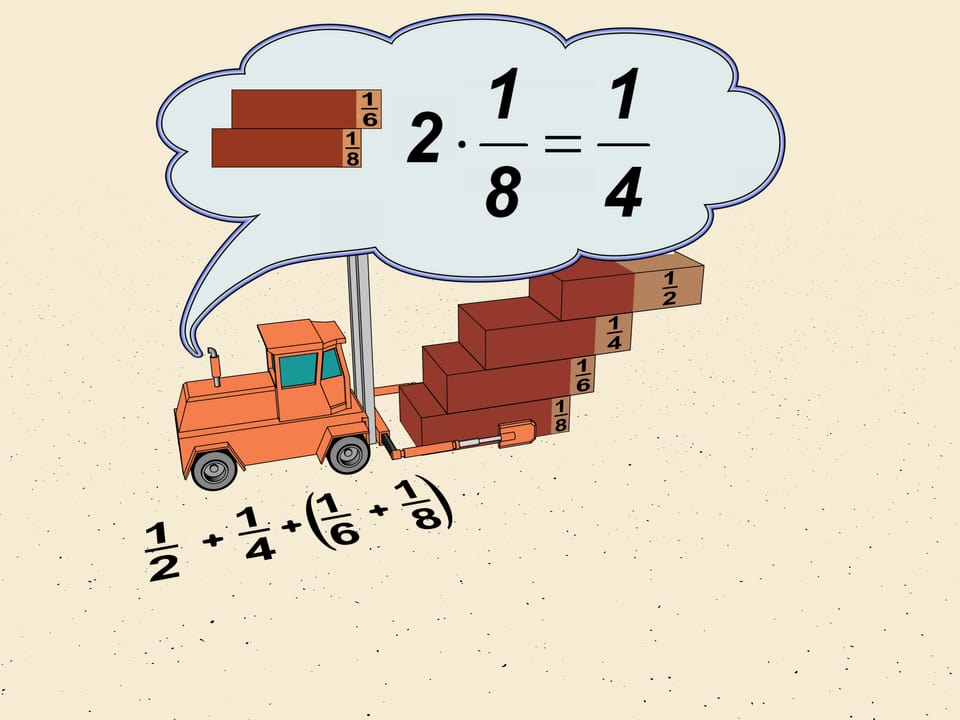
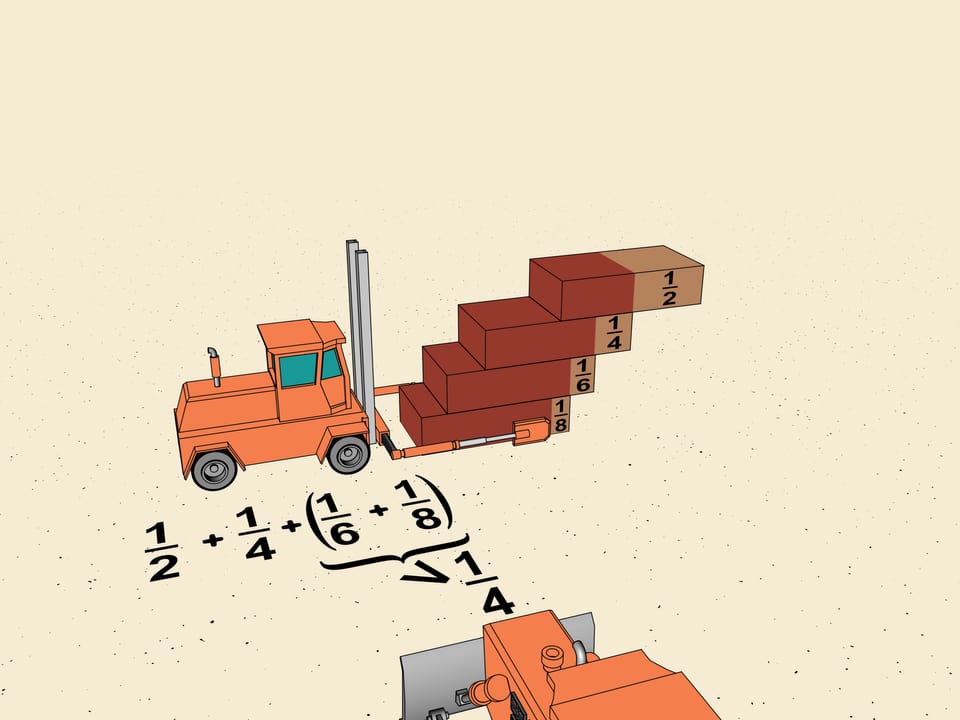
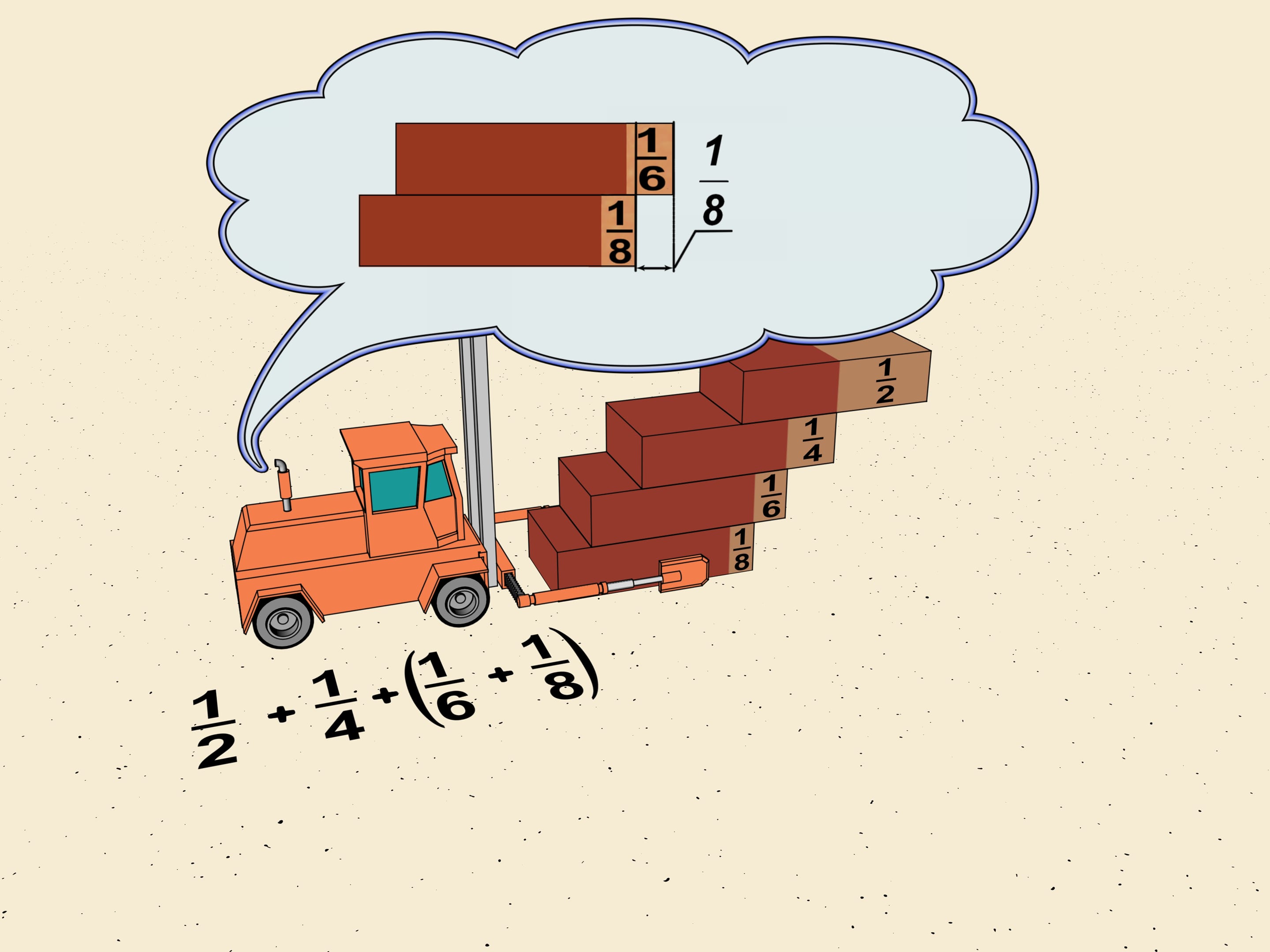
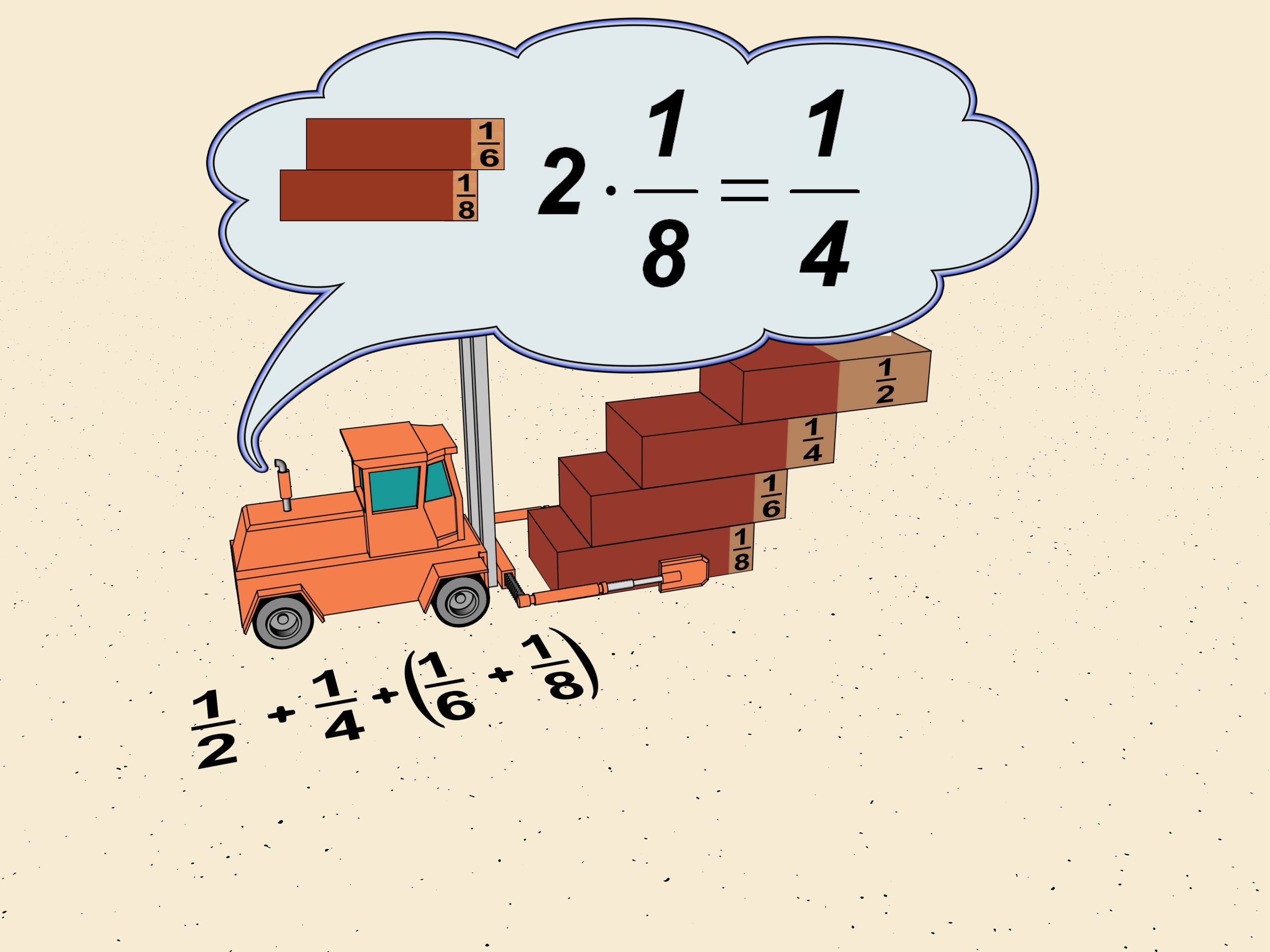
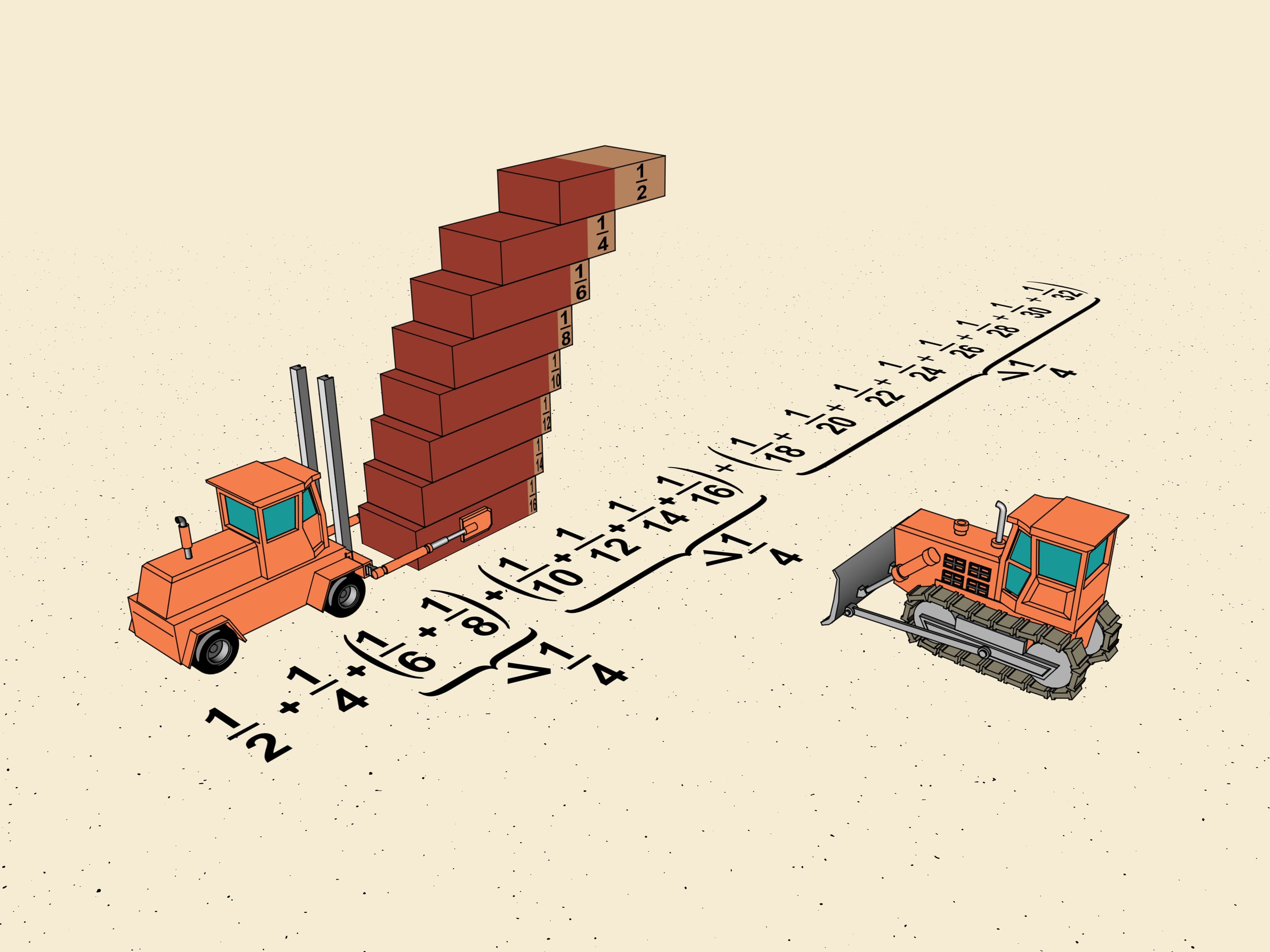
Observons les déplacements des premières briques de l'escalier: $1/2$, $1/4$, $1/6$, $1/8$. Laissant à part les deux premiers termes, nous regroupons $1/6$ et $1/8$ en ce que les mathématiciens appellent un "bloc". Déplaçons les bords des briques de façon que tous les déplacements dans le bloc sont les mêmes, et égaux au plus petit, c'est-à-dire à $1/8$. Le déplacement totale à ajouter est de $2\cdot1/8=1/4$ de la longueur d'une brique.
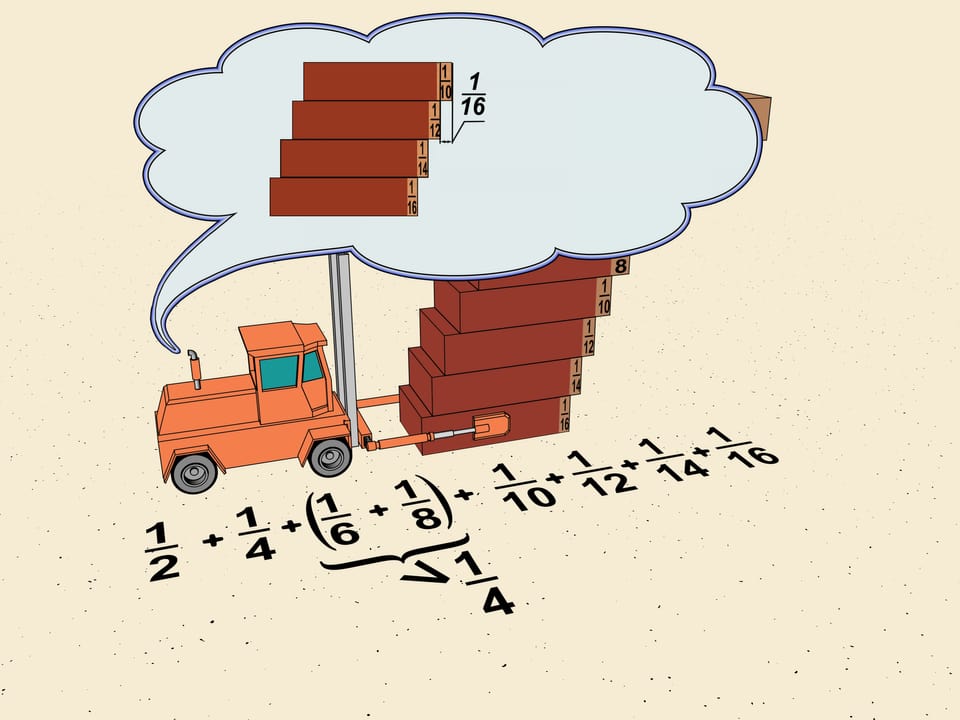
Bien sûr, nous sommes libres de diviser notre escalier en blocs comme il nous plait. Le bloc suivant sera composé de quatre briques. Cela correspond à un déplacement total de $1/10 + 1/12 + 1/14 + 1/16$. Pour estimer le déplacement dans chaque bloc, nous allons procéder de la même façon. Nous répétons ce que nous avons fait avec le premier bloc, c'est à dire déplaçons les briques de sorte que leurs déplacements sont tous égaux au minimum dans ce bloc. Nous obtenons que notre escalier en horizontale se déplace 4 fois $1/16$, soit $4\cdot 1/16 = 1/4$ de la longueur d'une brique. Cela signifie que le déplacement en horizontale de l’escalier du à ce bloc était à l’origine plus que $1/4$ de la longueur d'une brique.
Est-ce que vous avez compris la règle générale ? Le bloc suivant sera composé de $2^{3}$ briques, et le déplacement plus petit sera de $1/2^{5}$ de la longueur d'une brique, de sorte que le déplacement total, donné par ce bloc, sera lui aussi supérieur à $1/4=2^{3}\cdot1/2^{5}$.
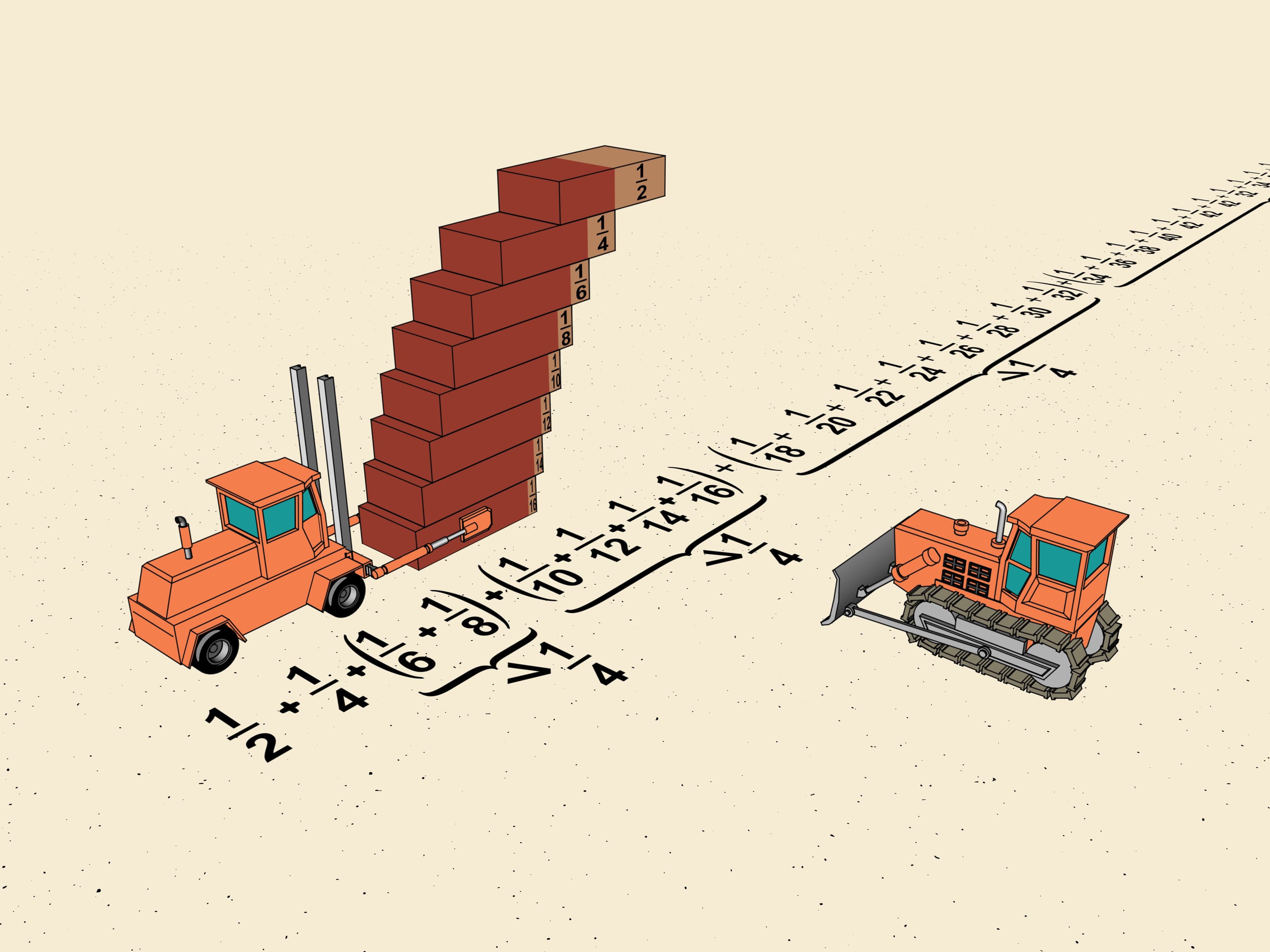
De cette façon, tout l’escalier peut être divisé en blocs. Le $n$-ième bloc sera composé de 2$n$ briques, et le moindre déplacement dans ce bloc sera $1/2^{n+2}$ la longueur d'une brique. La longueur totale du bloc sera supérieure $2^n\cdot{1/2}^{n+2}=1/4$.
Il est maintenant évident que lorsque le nombre $n$de blocs tend vers l'infini, la longueur de l'escalier à l’horizontale, qui est supérieure à $n$/4, ira à l'infini.
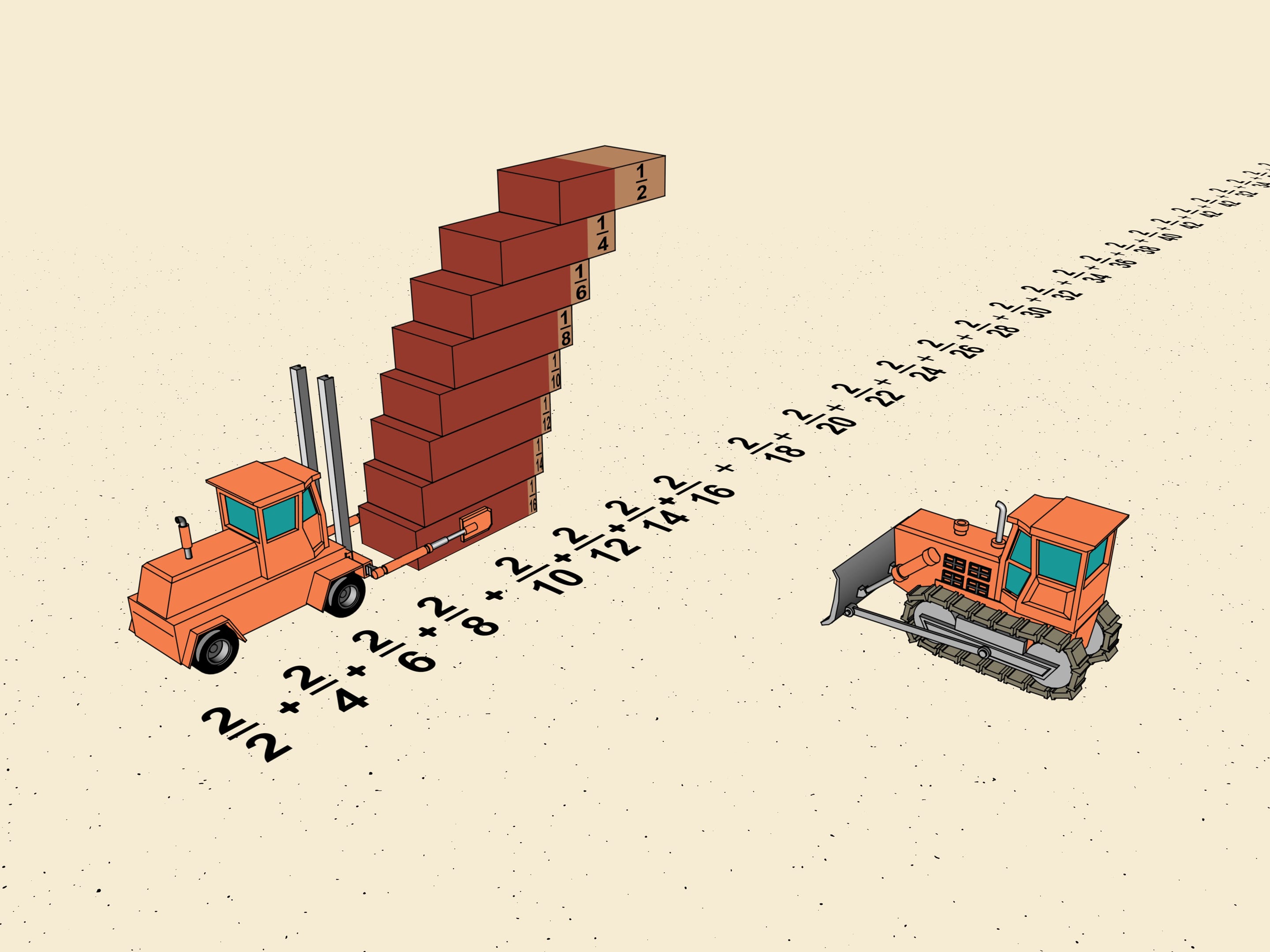
Multiplions par $2$ chaque terme de la série, puis nous réduisons les fractions. Nous obtenons la série $1+1/2+1/3+1/4+1/5+1/6+1/7+...+1/n+...$ Cette série est appelée harmonique. Elle joue un rôle important parmi les séries, une sorte de «frontière». Si vous construisez un escalier (déjà à l'aide du ciment), avec des déplacements plus grand que $1/n$ (c’est-à-dire, le dénominateur sera un nombre inférieur à $n$), cet escalier ira à l'infini dans la direction horizontale.
En mathématiques, cette propriété est appelée la «divergence de la série » et signifie que étant donné un nombre aussi grand que l’on veut, on peut toujours trouver un certain nombre de termes de la série tels que leur somme est supérieure au nombre donné. Un des critères de divergence est juste la comparaison avec la série harmonique.
En s’éloignant, les conducteurs des machines se disent:
– C'est incroyable, vraiment l'escalier va arriver jusqu’à ce point?
– Nous venons de le prouver : nous pouvons prendre n'importe quel nombre de blocs, dont chacun dépasse $1/4$ de la longueur d'une brique ...