Nous allons prendre des mesures. Toutefois, avant de mesurer quelque chose, il faut toujours définir l’unité de mesure avec laquelle on prendra les mesures. Les garçons russes se souviennent d’une chanson qui dit «Mais en perroquets je suis beaucoup plus haut!»
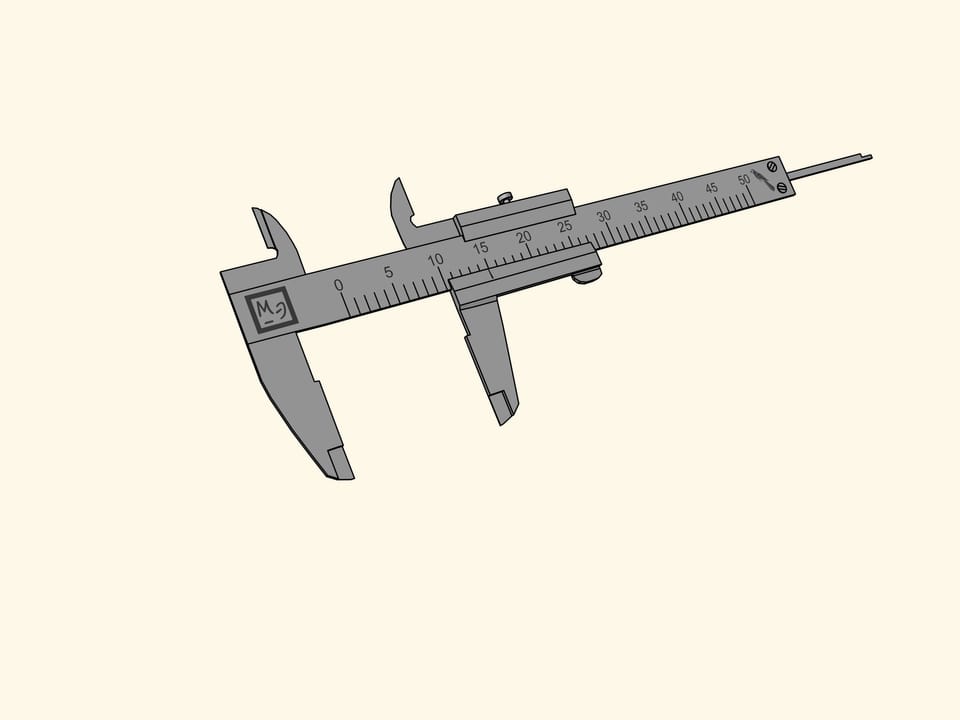
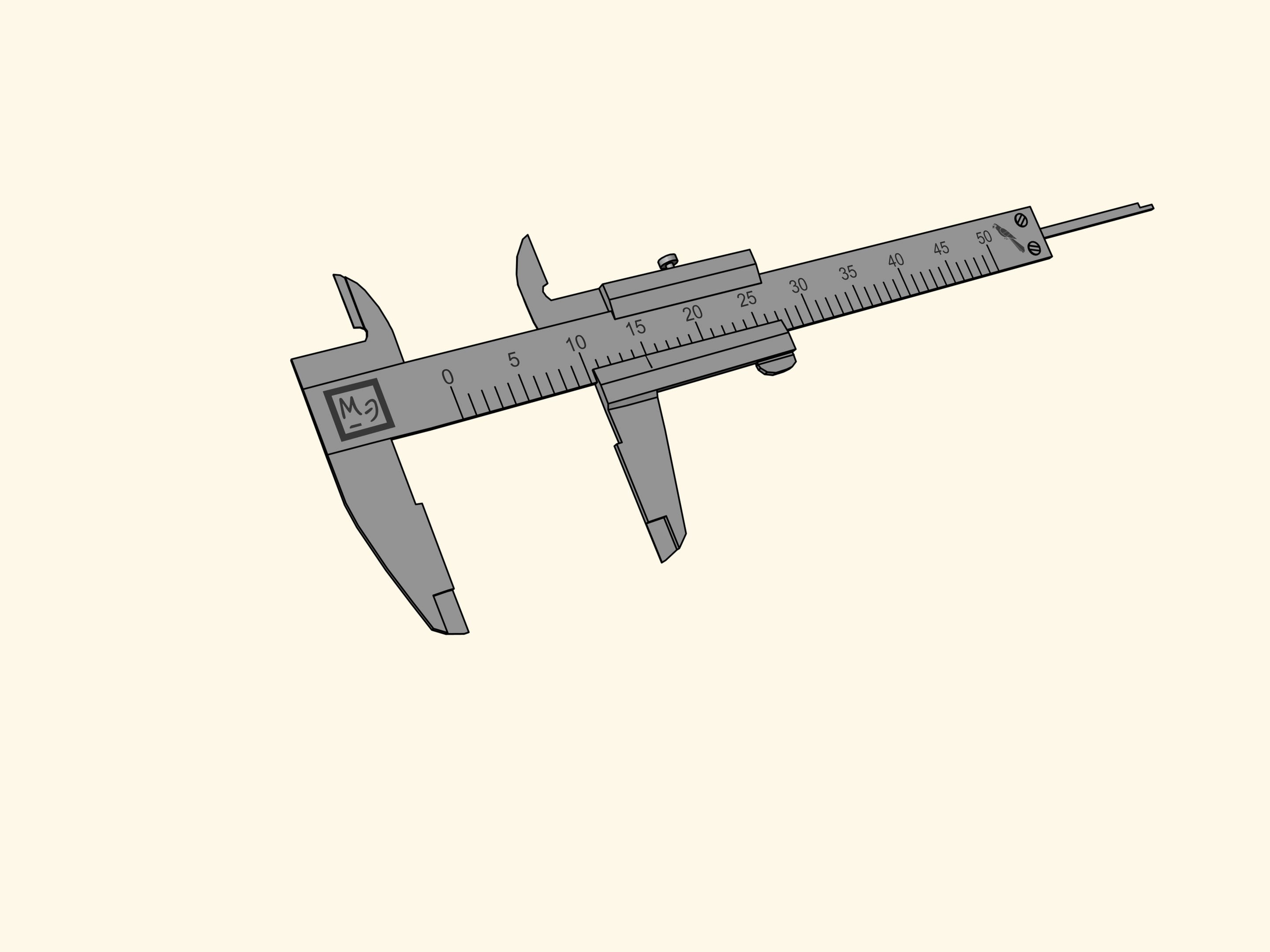
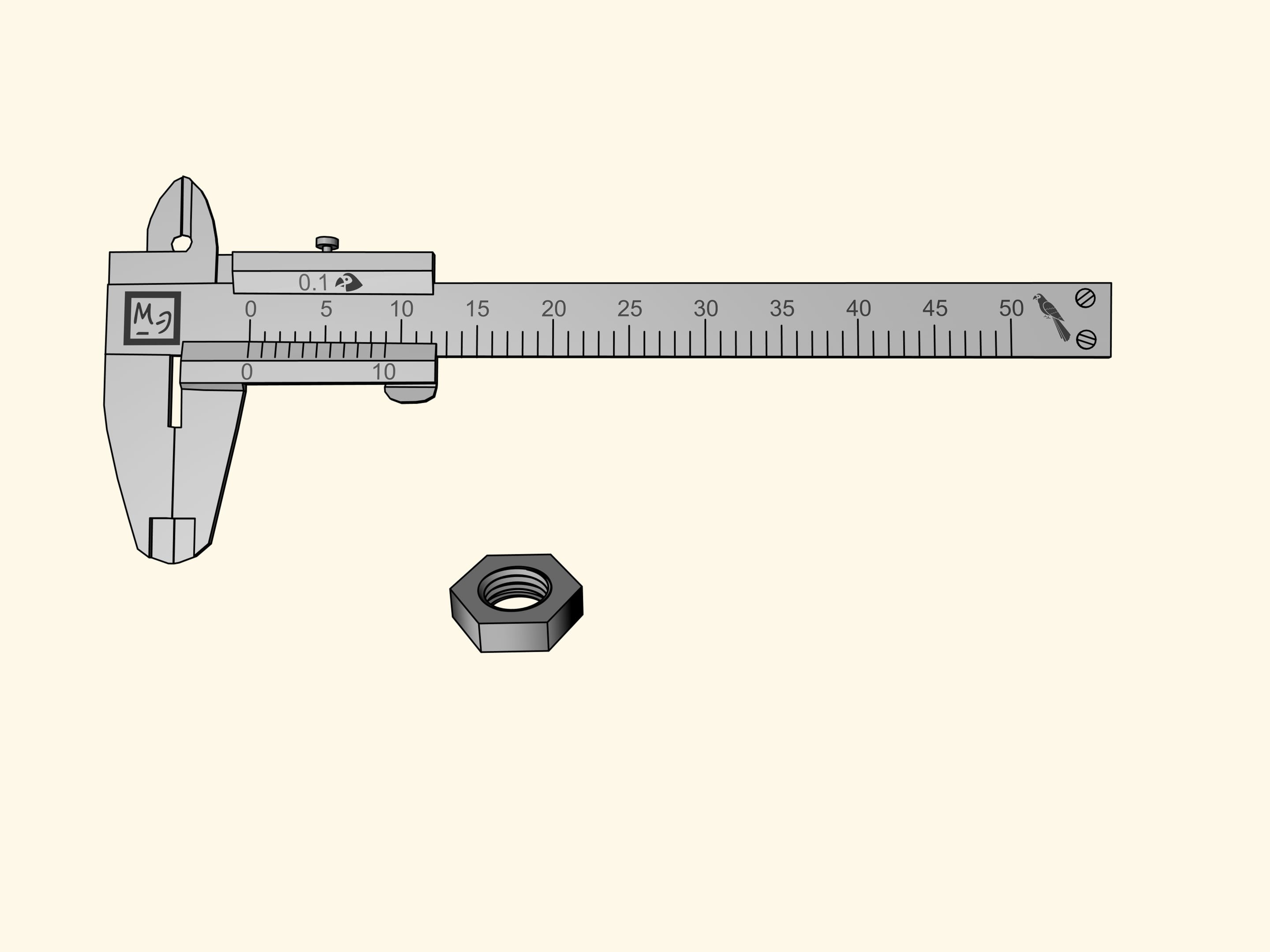
Comment faut–il mesurer «en perroquets» par un pied à coulisse? Les têtes situées inférieurement è la règle fixe graduée son utilisées pour les dimensions extérieures, quand il faut mesurer, par exemple, le diamètre extérieur d’un tuyau. Les ergots qui se trouvent supérieurement à la règle graduée sont utilisées pour les dimensions intérieures, comme, par exemple, le diamètre intérieur d’un tuyau. Pour finir, il y a encore une «queue» qui affleure le bout de la règle, pour mesurer la profondeur, par exemple, d’un trou. Ces trois parties sont fixées à une barre coulissant qui mesure 15 perroquets.
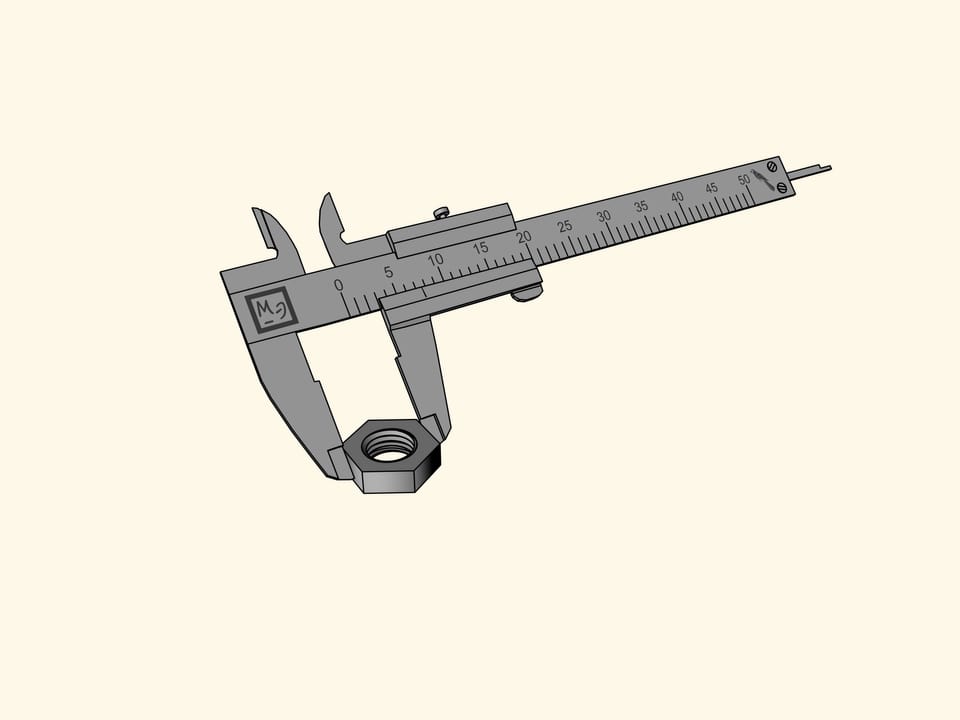
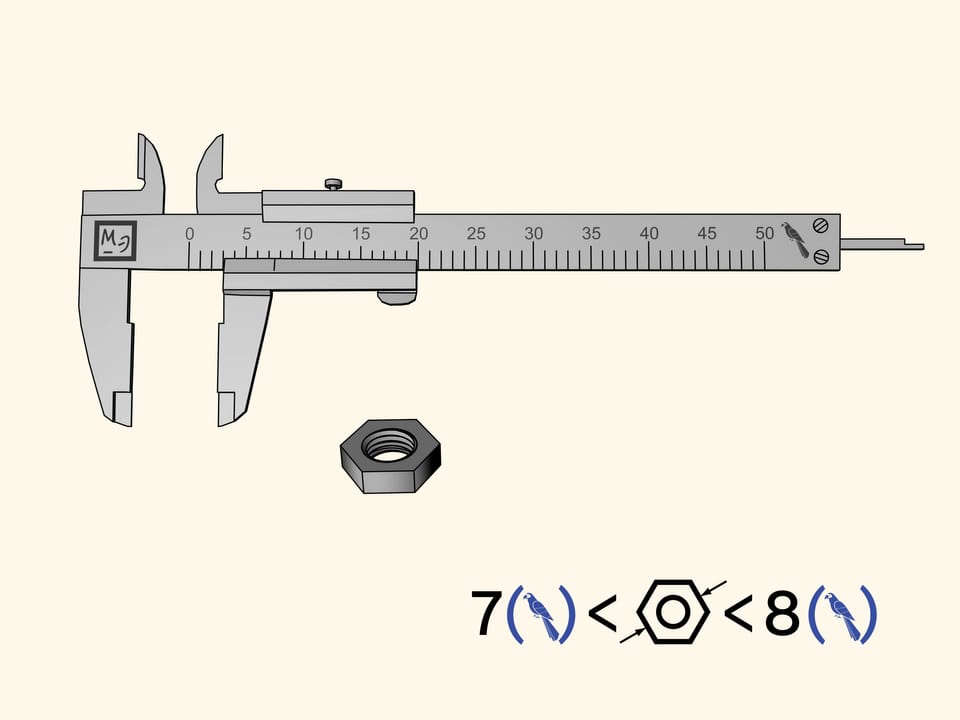
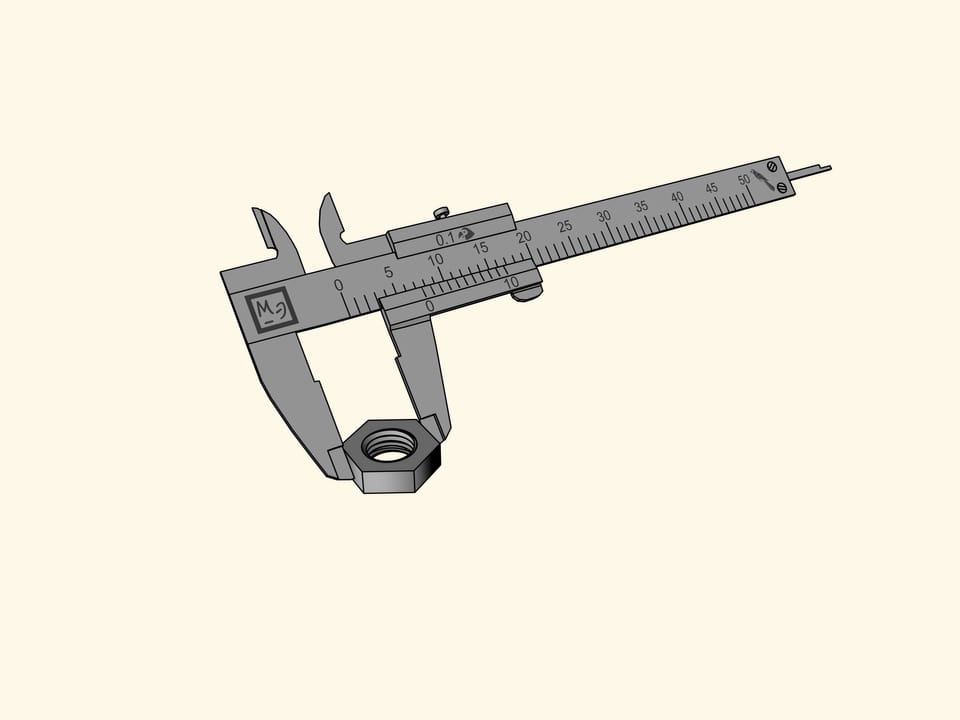
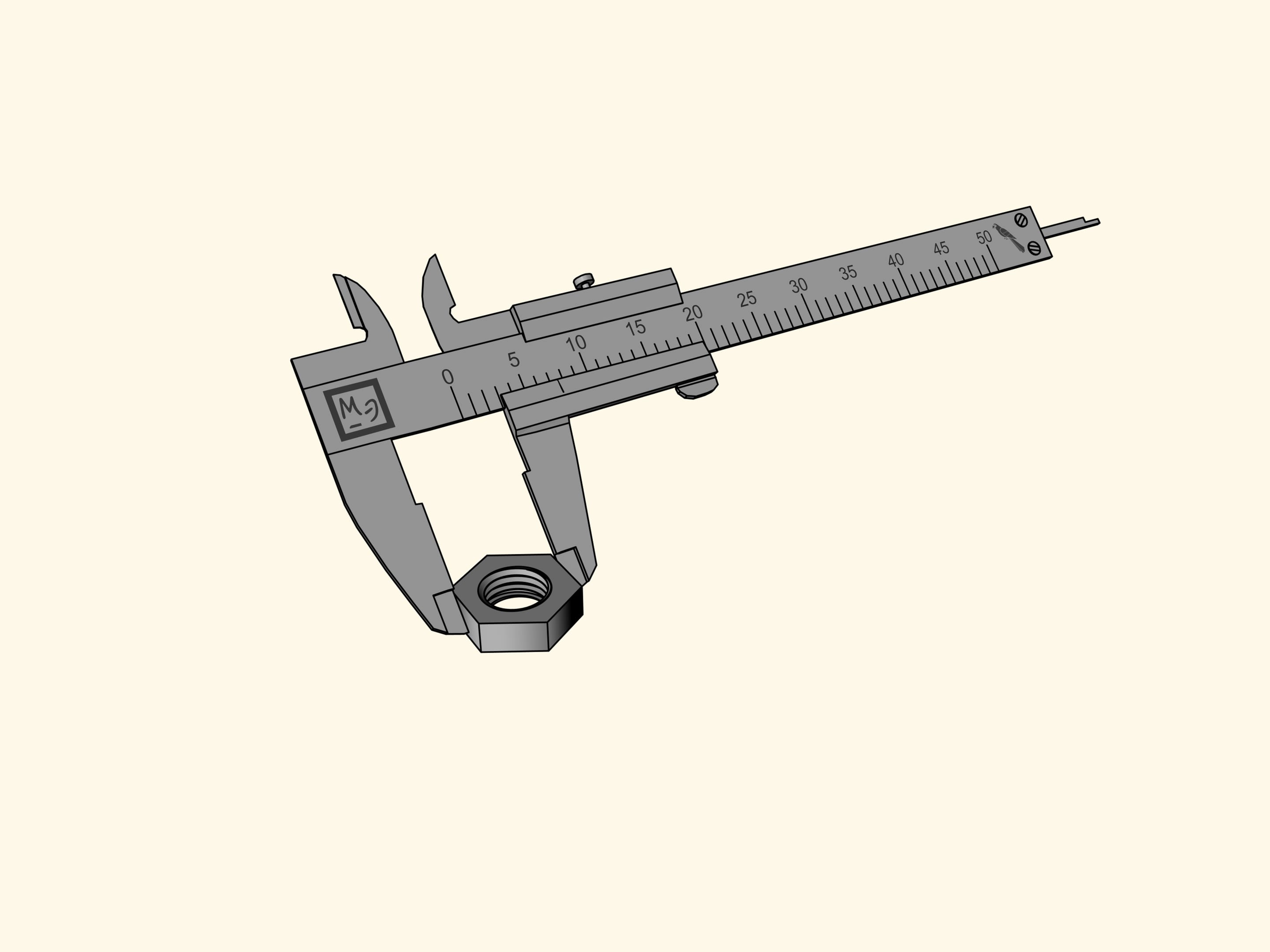
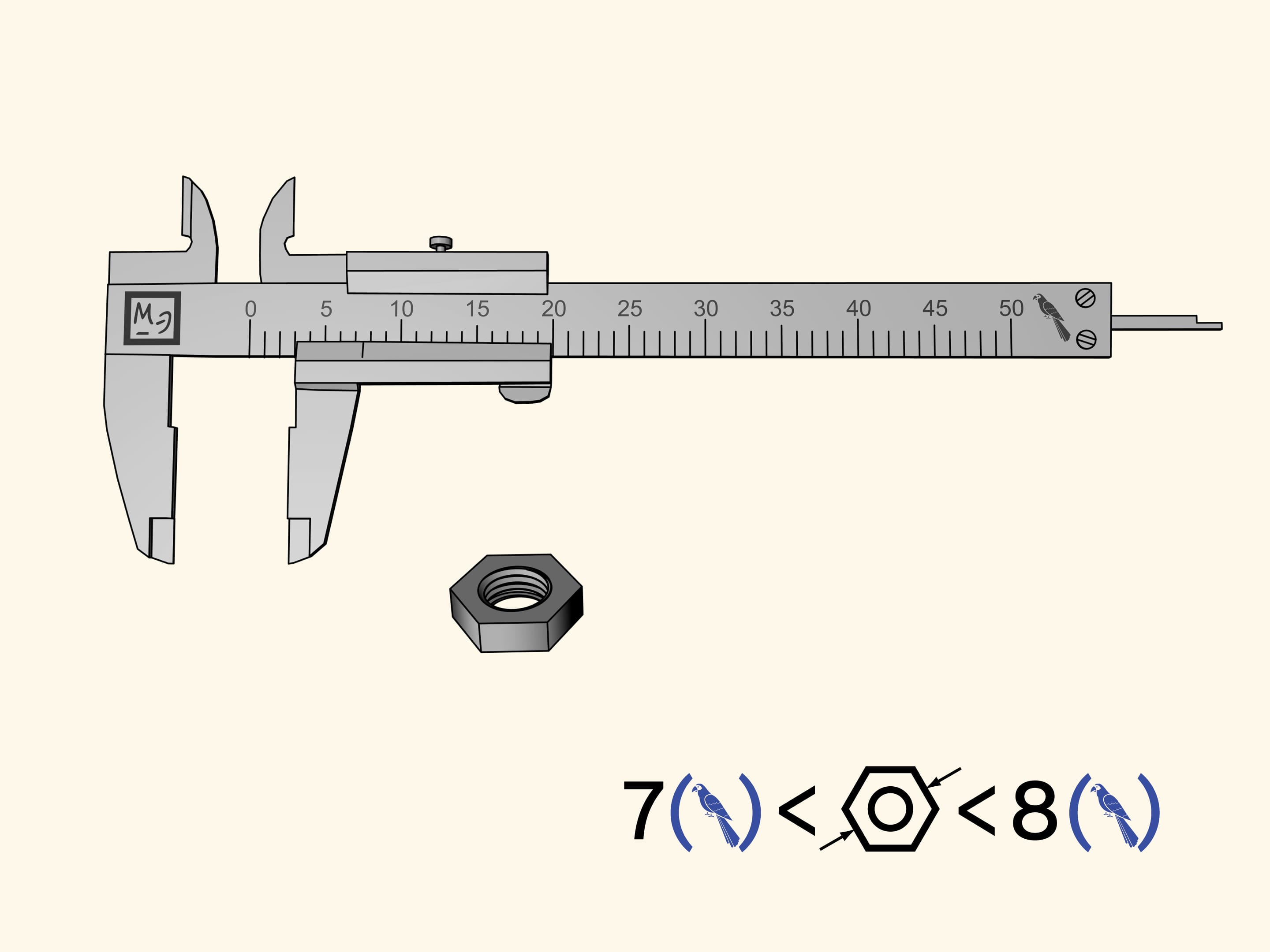
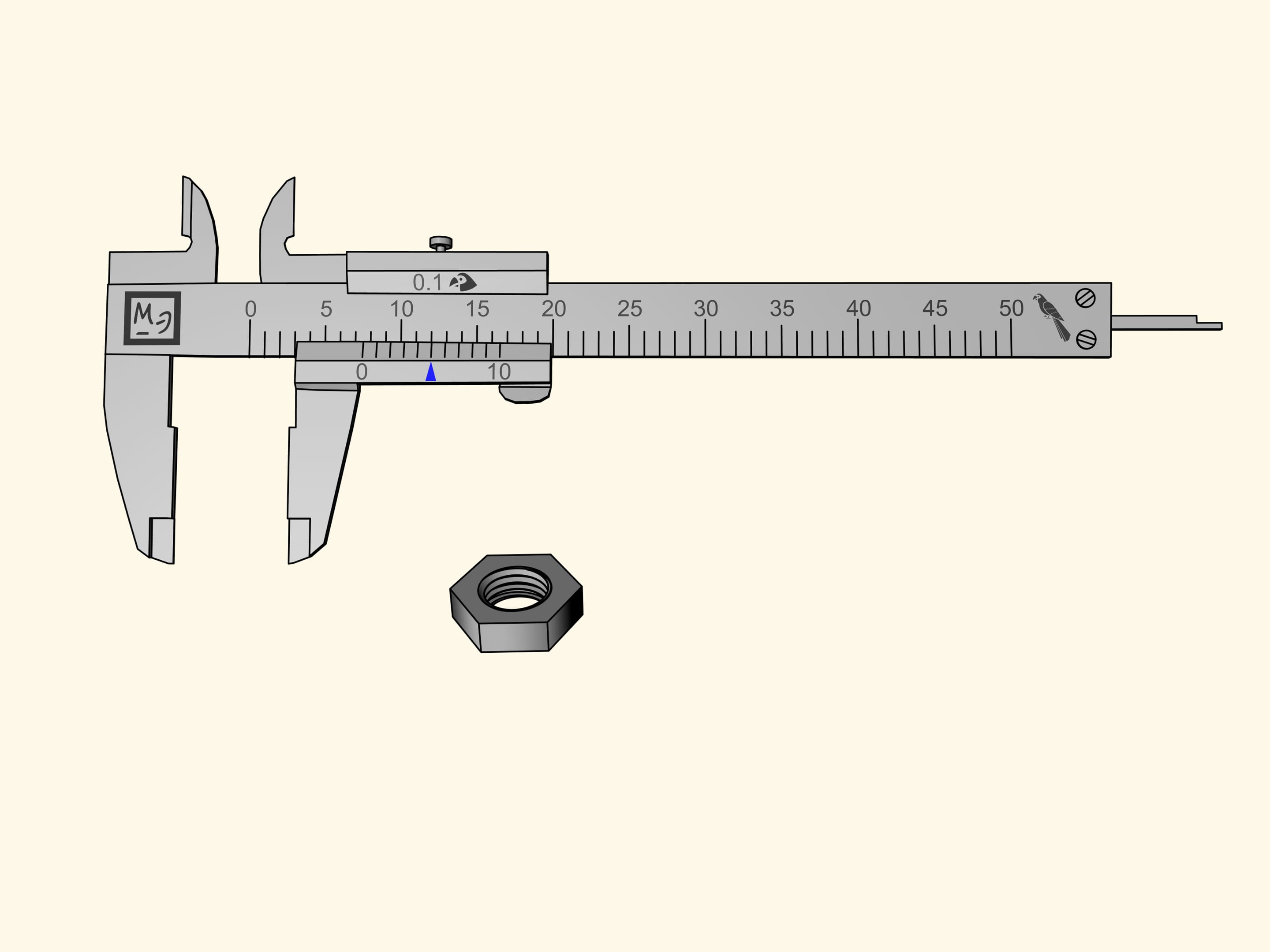
Nous allons mesurer un écrou hexagonal. Malheureusement, l’encoche du zéro de la barre coulissant, qui indique la taille de l’écrou, se trouve entre deux divisions de la règle principale. Tout ce que cette mesure nous permet de dire c’est que l’écrou est plus de sept perroquets, mais moins de huit. Il est difficile de définir sa taille plus précisément par l’oeil.
Une méthode qui ne complique pas la construction du même pied à coulisse, mais permet des résultats plus précis, a été inventée il ya quelques siècles. Il ne s’agit que d’ajouter sur la barre coulissante une échelle graduée supplémentaire, le vernier.
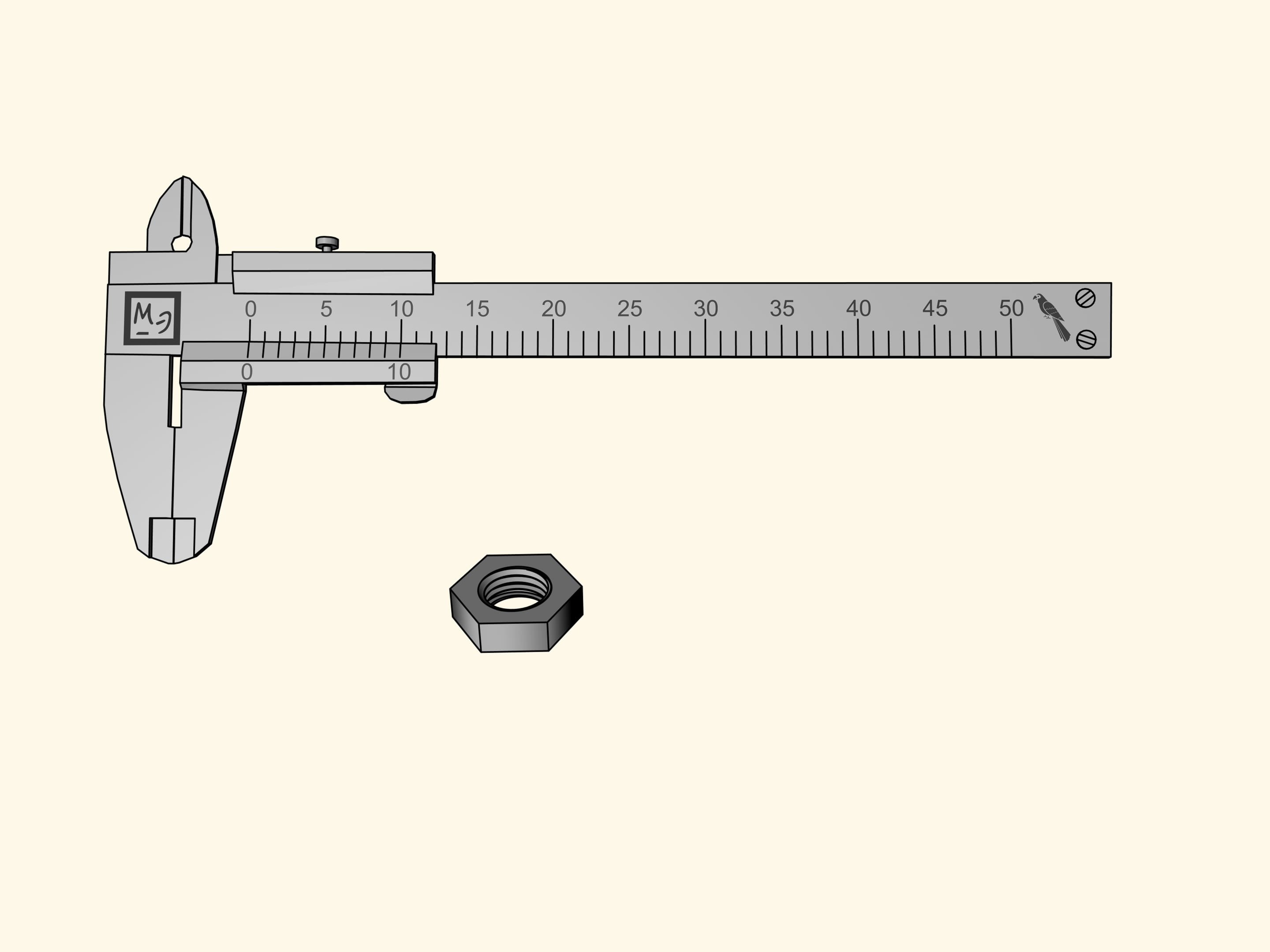
Sur la barre coulissant marquons dis encoches après le zéro de référence, qui coïncident avec celles de la règle principale. Maintenant on comprime uniformément ces dis divisions de façons qu’elles occupent neuf divisions de l’échelle principale. Ce dispositif fut inventé en 1631 par le mathématicien Pierre Vernier. Dans certaines langues, il porte le nom de nonius, nom latinisé de l’astronome et mathématicien portugais Pedro Nunes (1502—1578), qui avait inventé, avant Vernier, un système pareil.
Il arrive que la règle supplémentaire construite de cette manière permet de faire des mesures avec une précision de $0{,}1$ perroquets. Mais comment?
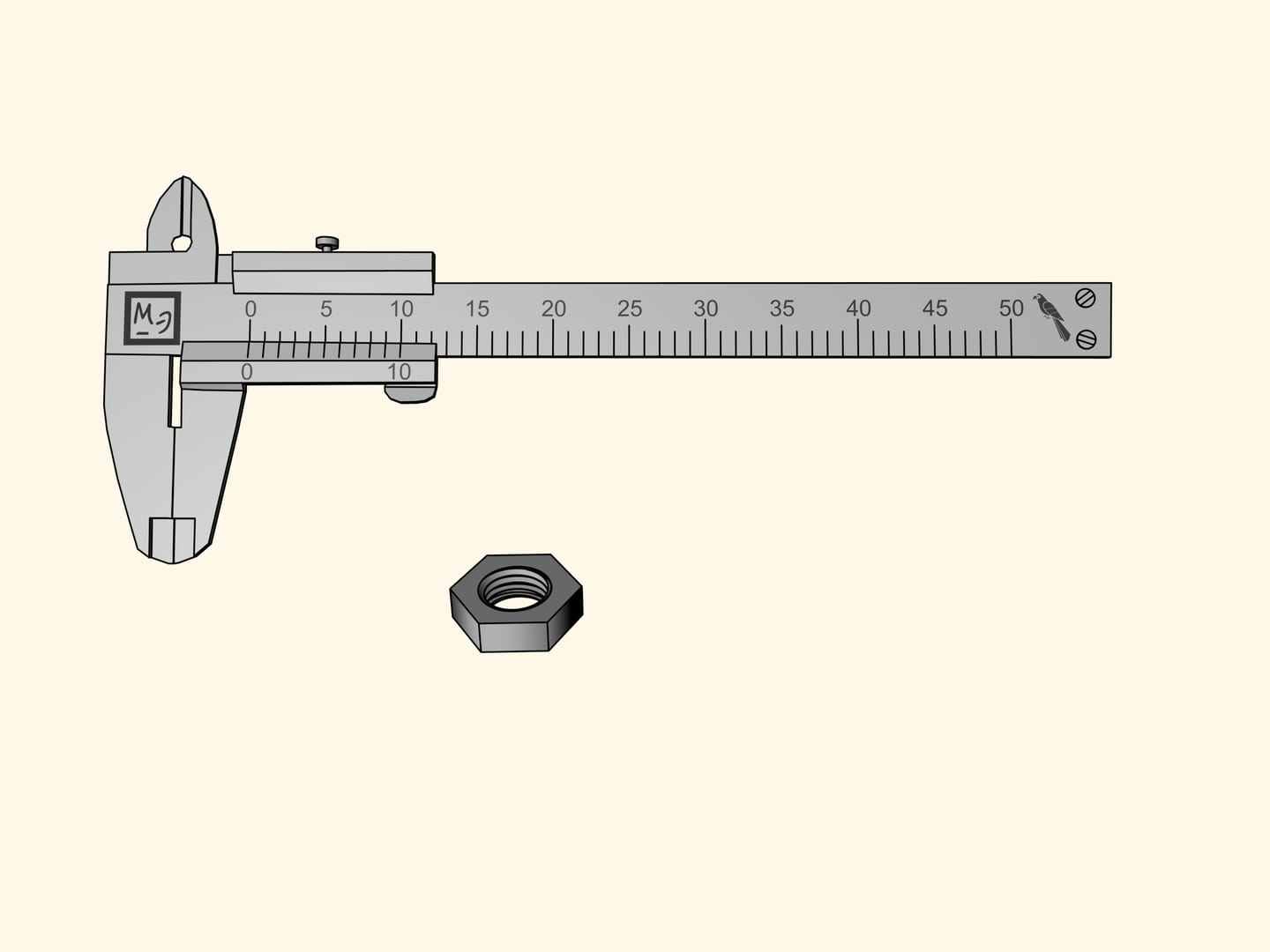
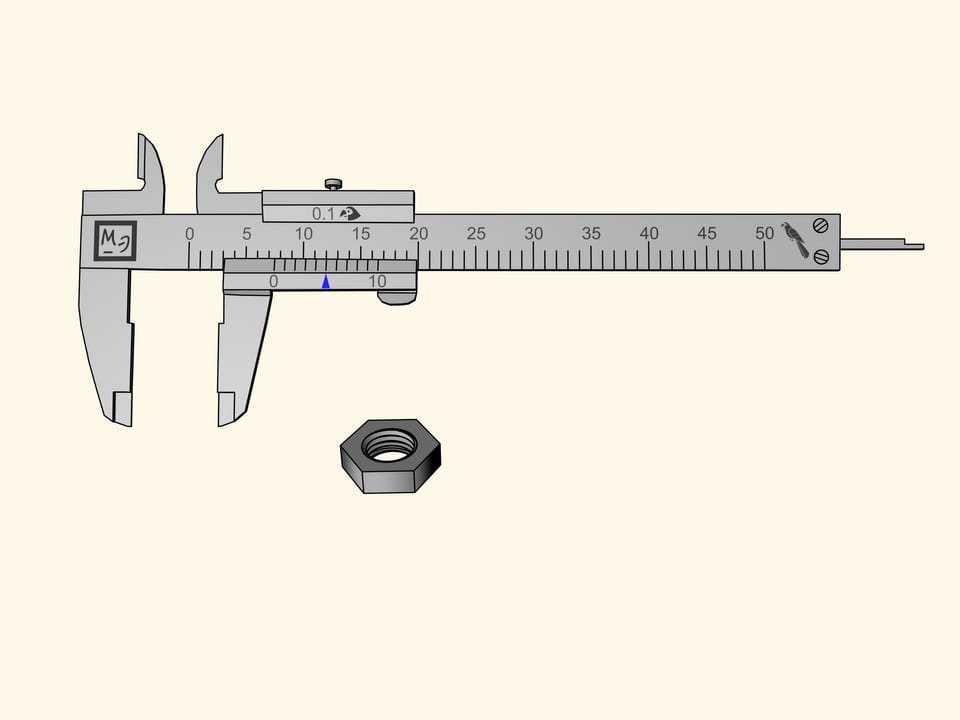
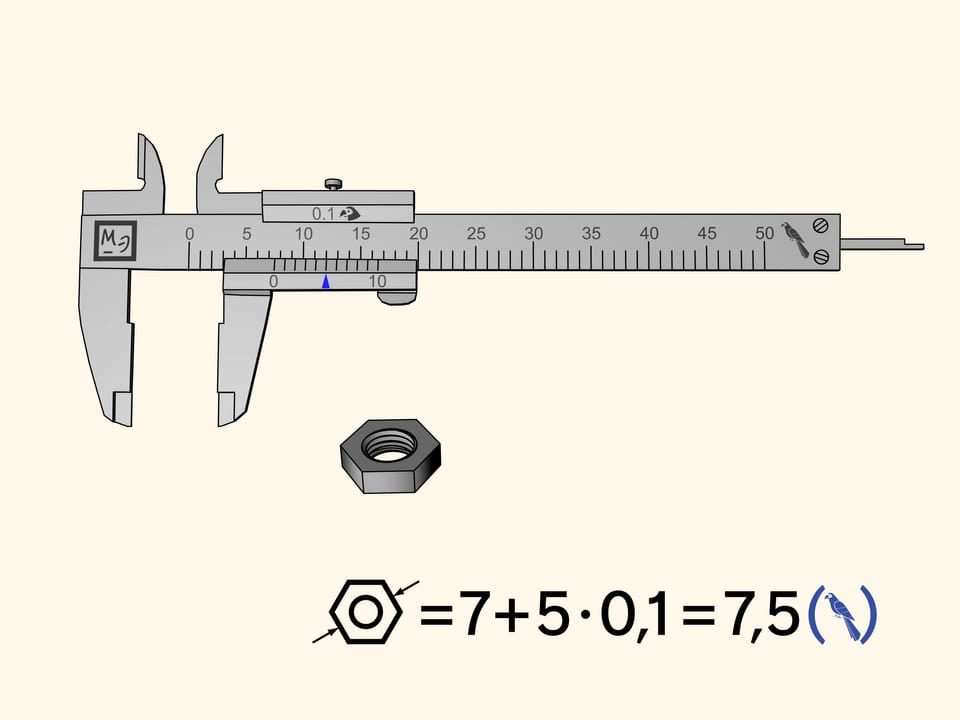
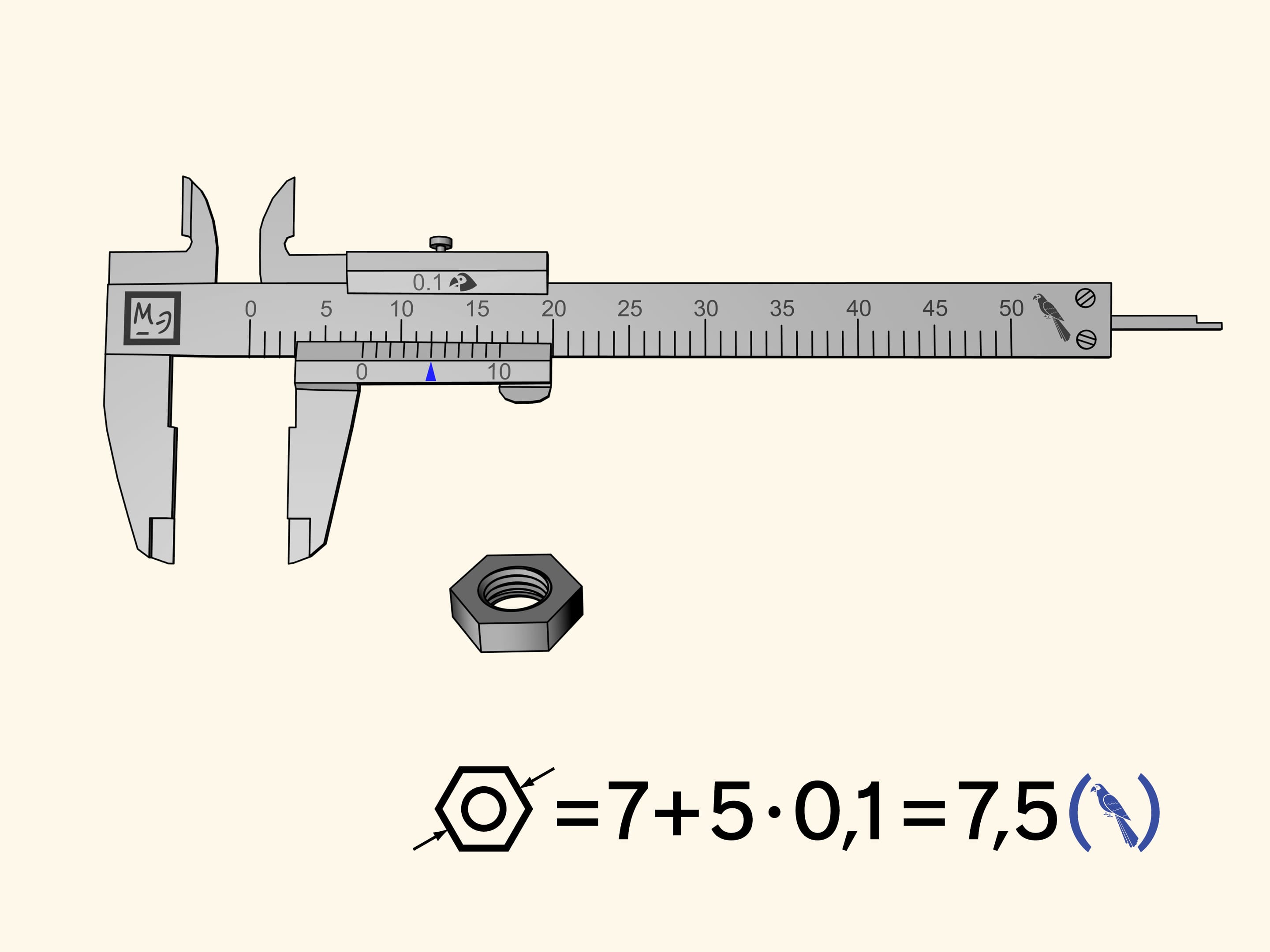
Nous mesurons l’écrou à nouveau. Le zéro de référence de la barre coulissante sera, comme avant, entre la septième et la huitième division. Cela signifie que notre mesure contient sept perroquets entiers. Maintenant observons les encoches de la règle supplémentaire de gauche à droite et cherchons celle qui coïncide avec l’une des encoches de l’échelle principale. Dans notre cas, cela arrive à la cinquième encoche. Par conséquent, la mesure de l’écrou est égale à $7 + 5 × 0{,}1 = 7{,}5$ (perroquets).
Expliquez mathématiquement l’argument ci–dessus. Pensez à comment utiliser la même idée pour obtenir plus de précision.