Inventer la roue ⁠

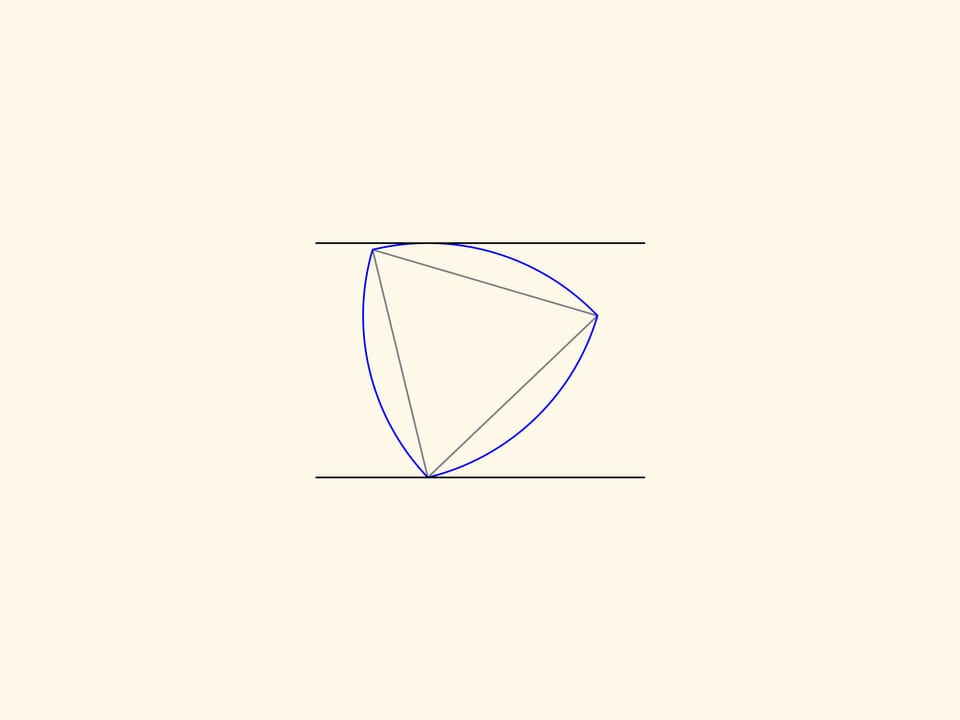
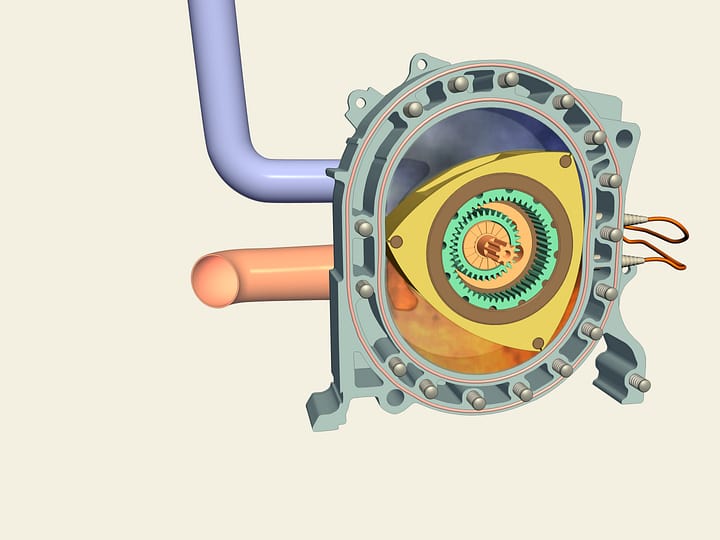
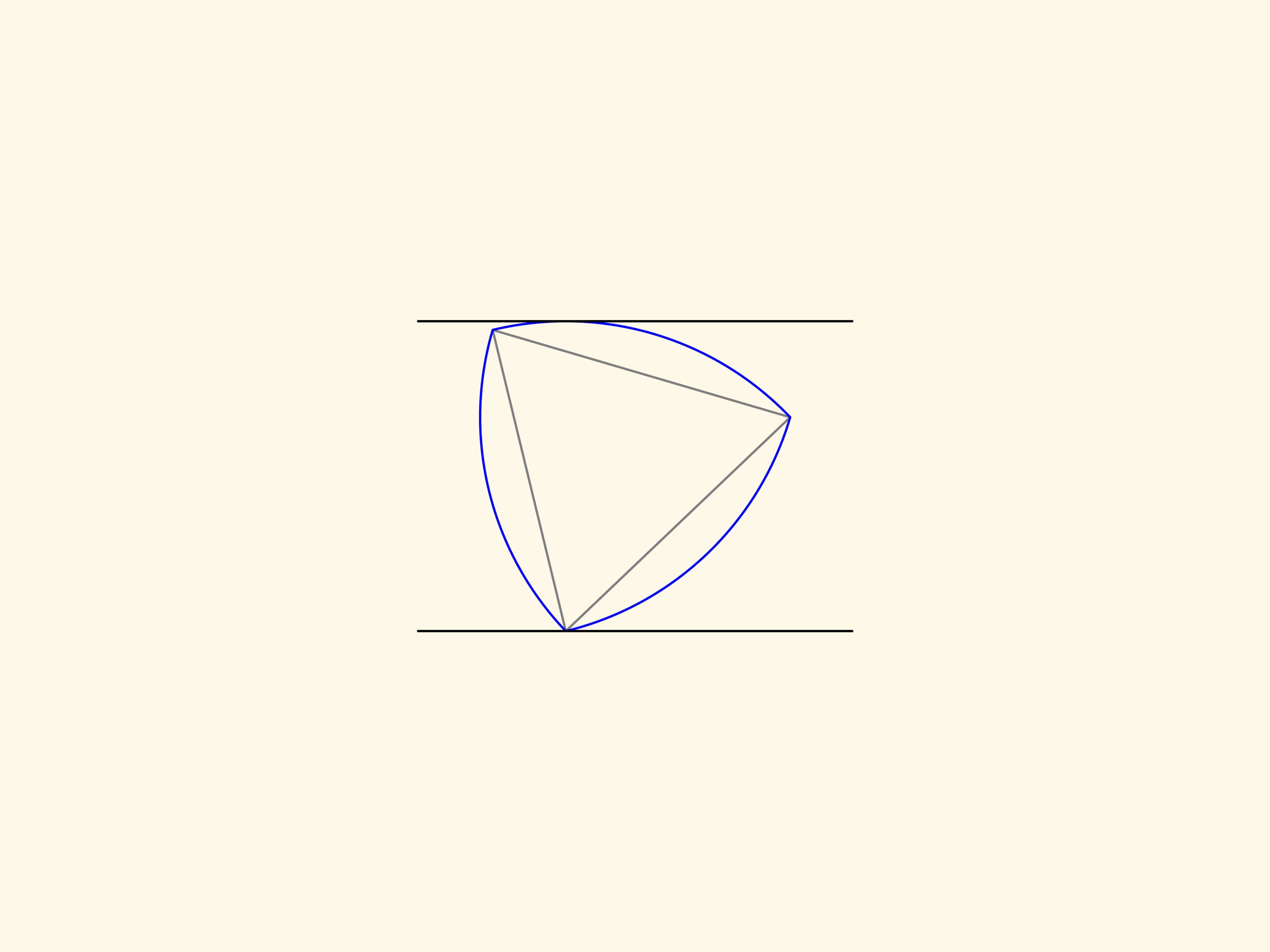
⁠⁠Le triangle de Reuleaux est une figure plane de largeur constante: il peut être tourné entre deux droites paral­lèles qui sont à une distance fixe, en restant en contact constant avec les deux.

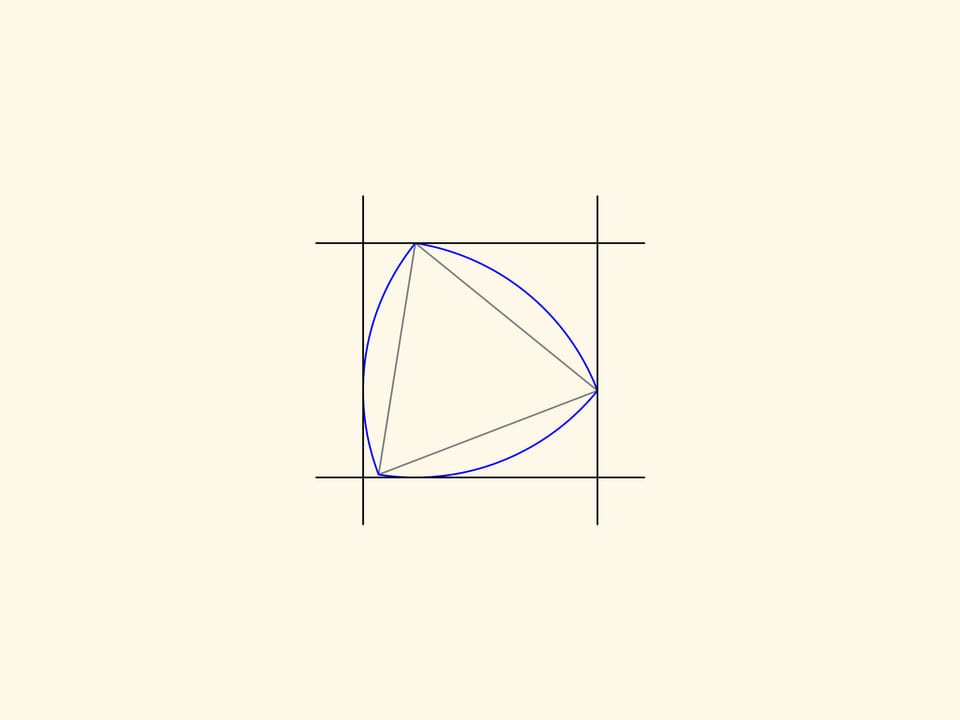
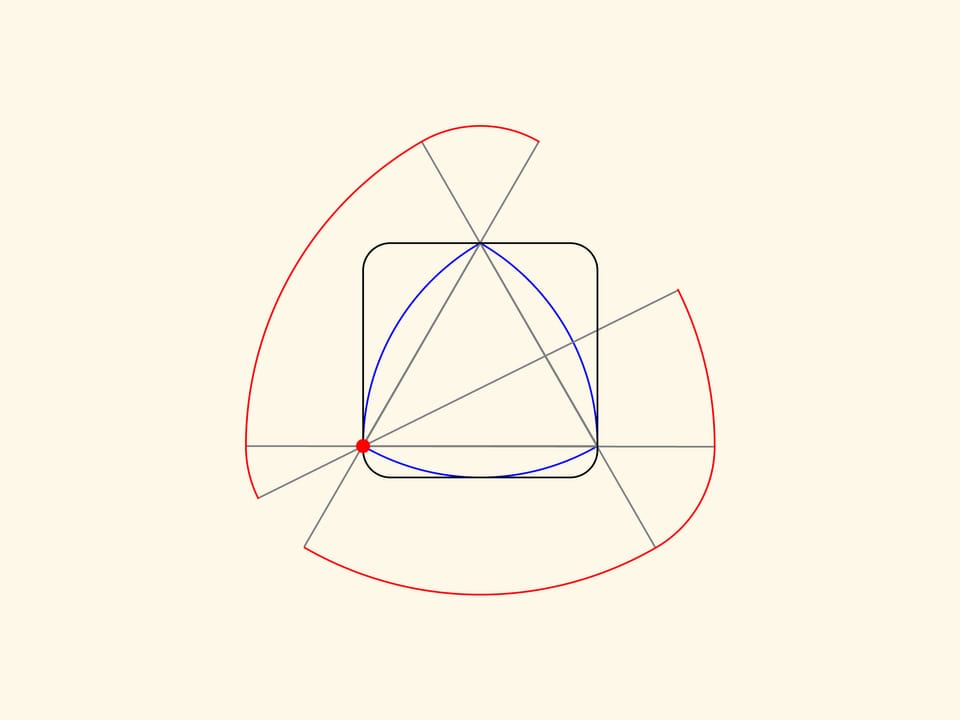
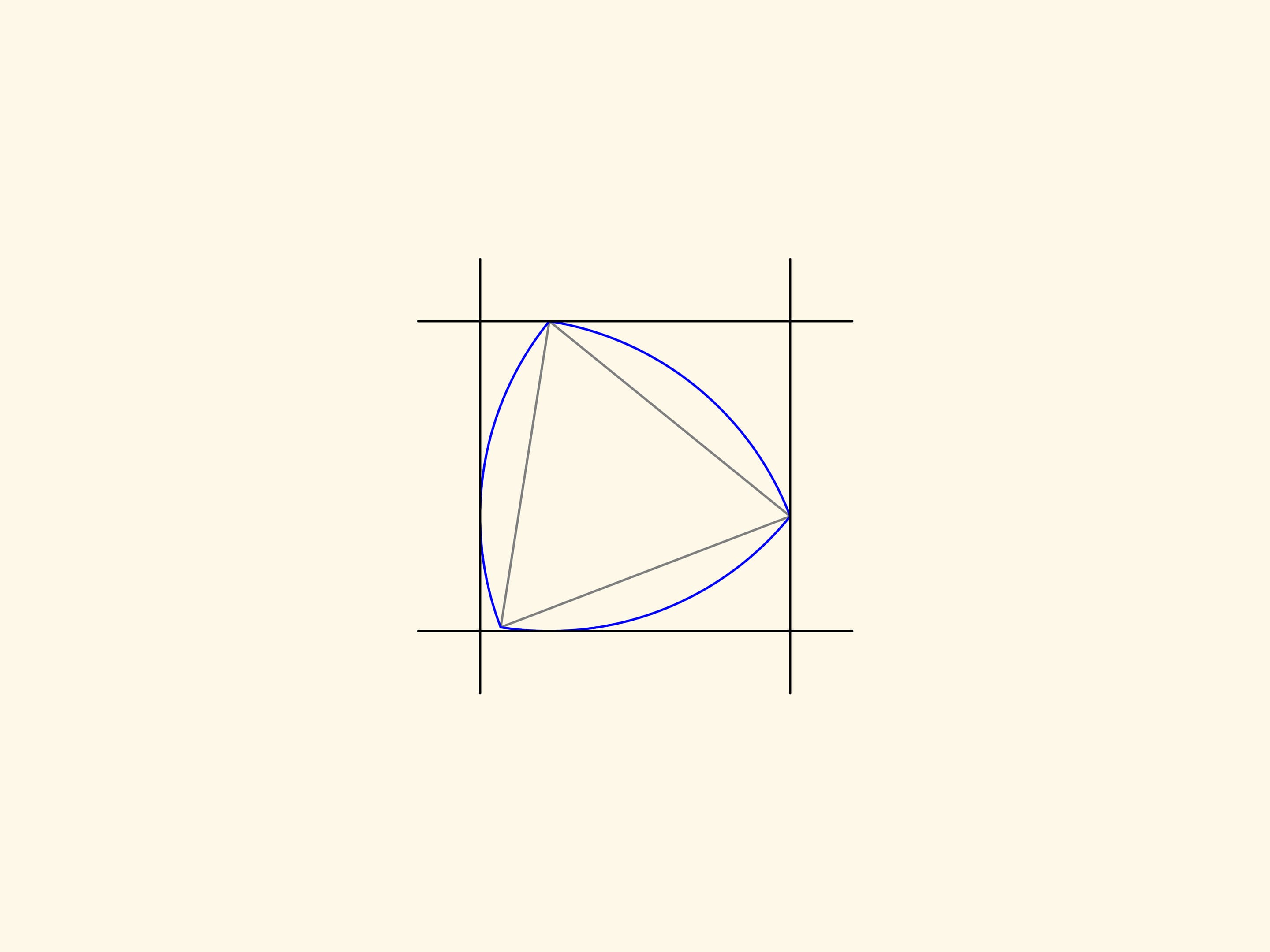
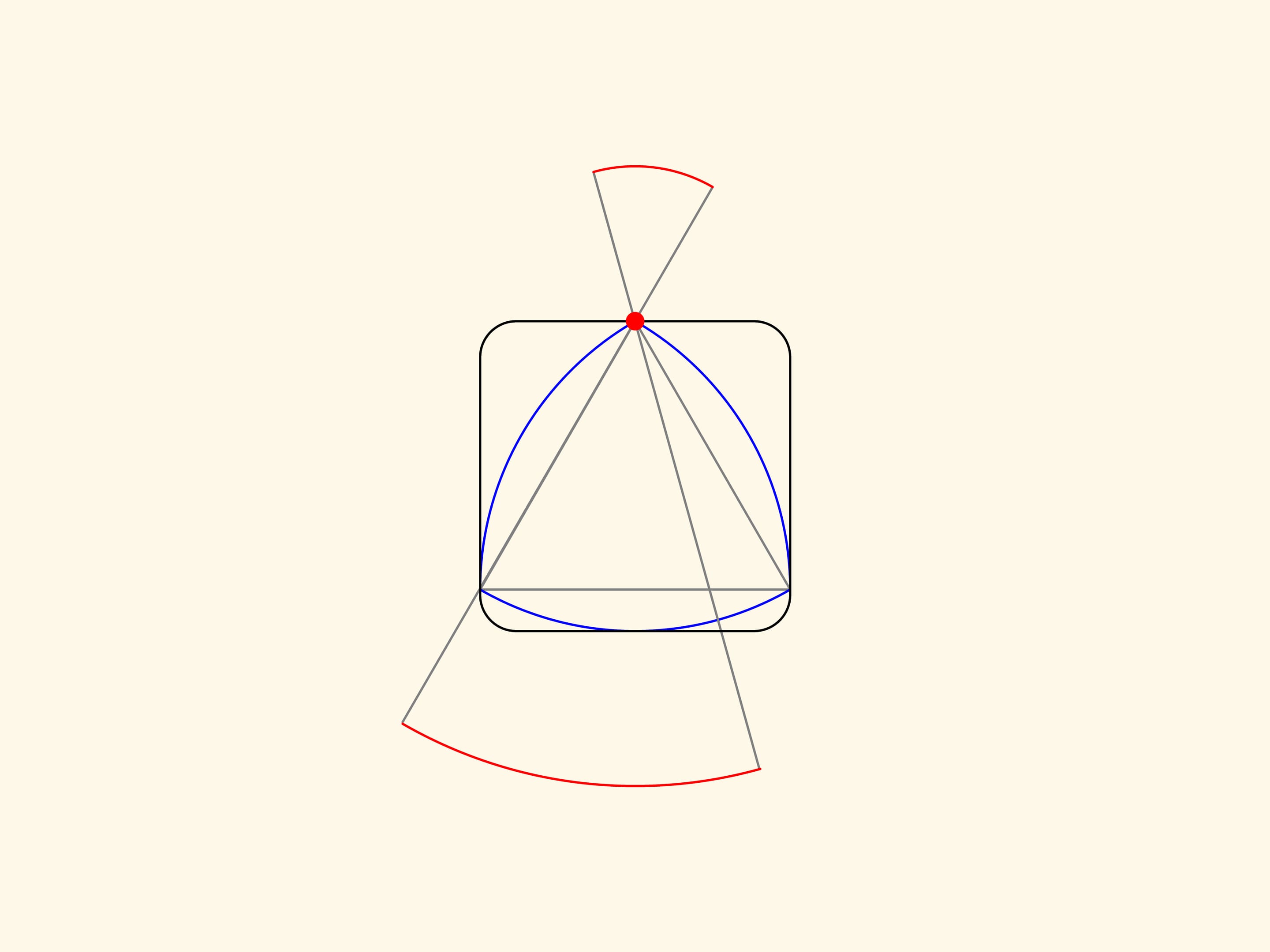
Ajou­tons une autre paire de droites paral­lèles tangentes au triangle et formant un angle droit avec celles déjà exis­tantes. Nous obte­nons un carré. Le triangle de Reuleaux, si l’on fait tourner de façon conve­nable, sera toujours à l’inté­rieur du carré et à tout moment en contact avec tous les côtés du carré.

Pour être plus précis, nous devrions prendre un carré avec les coins légè­re­ment arrondis. De cette façon, le triangle de Reuleaux résulte être, à l’inté­rieur de ce «carré», le rotor d’aire mini­male, c’est–à–dire une figure qui, n’importe comment tournée, touchera le «carré» en quatre points, et étant en outre la figure d’aire mini­male avec cette propriété.

Le cercle et le triangle de Reuleaux ne sont pas les seules ⁠⁠figures de largeur constante. Sur un poly­gone avec un nombre impair de côtés, ainsi que le triangle, nous pouvons construire une courbe de largeur constante. Il y a aussi des courbes asymé­triques de largeur constante.

Mais il y a aussi d’innom­brables autres figures de largeur constante, construites exac­te­ment sur le triangle équi­la­téral, et qui ne sont pas semblables, soit entre eux soit au triangle de Reuleaux.

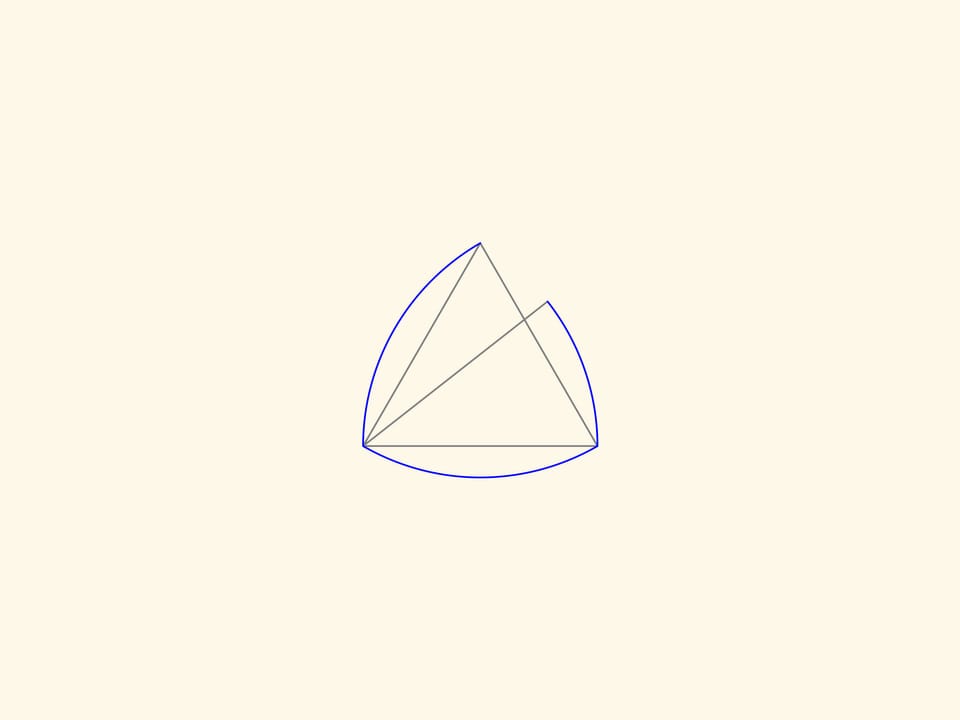
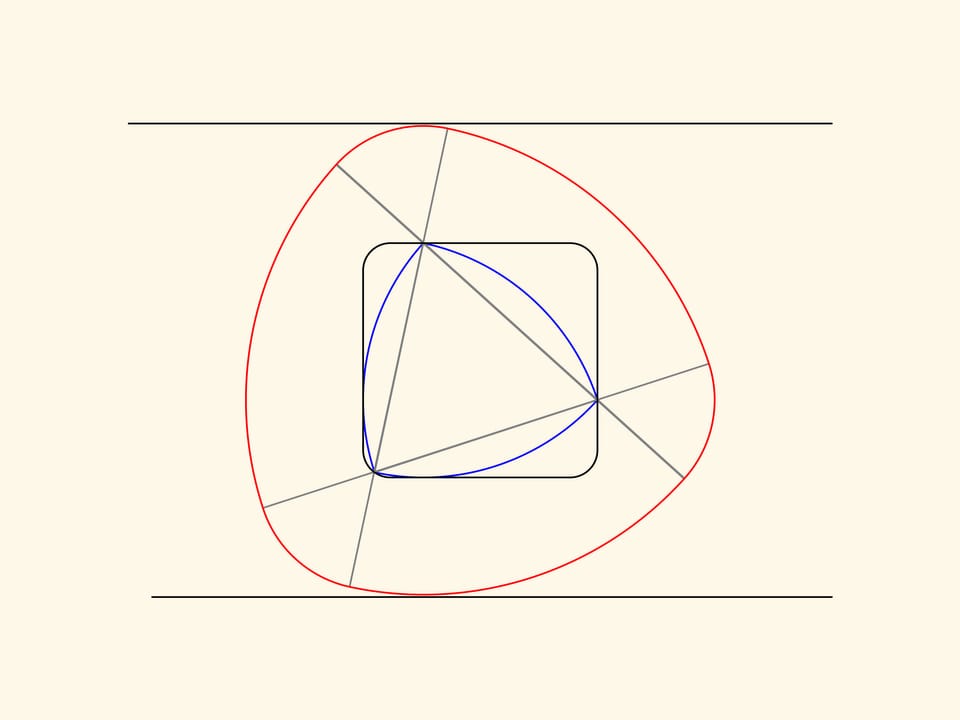
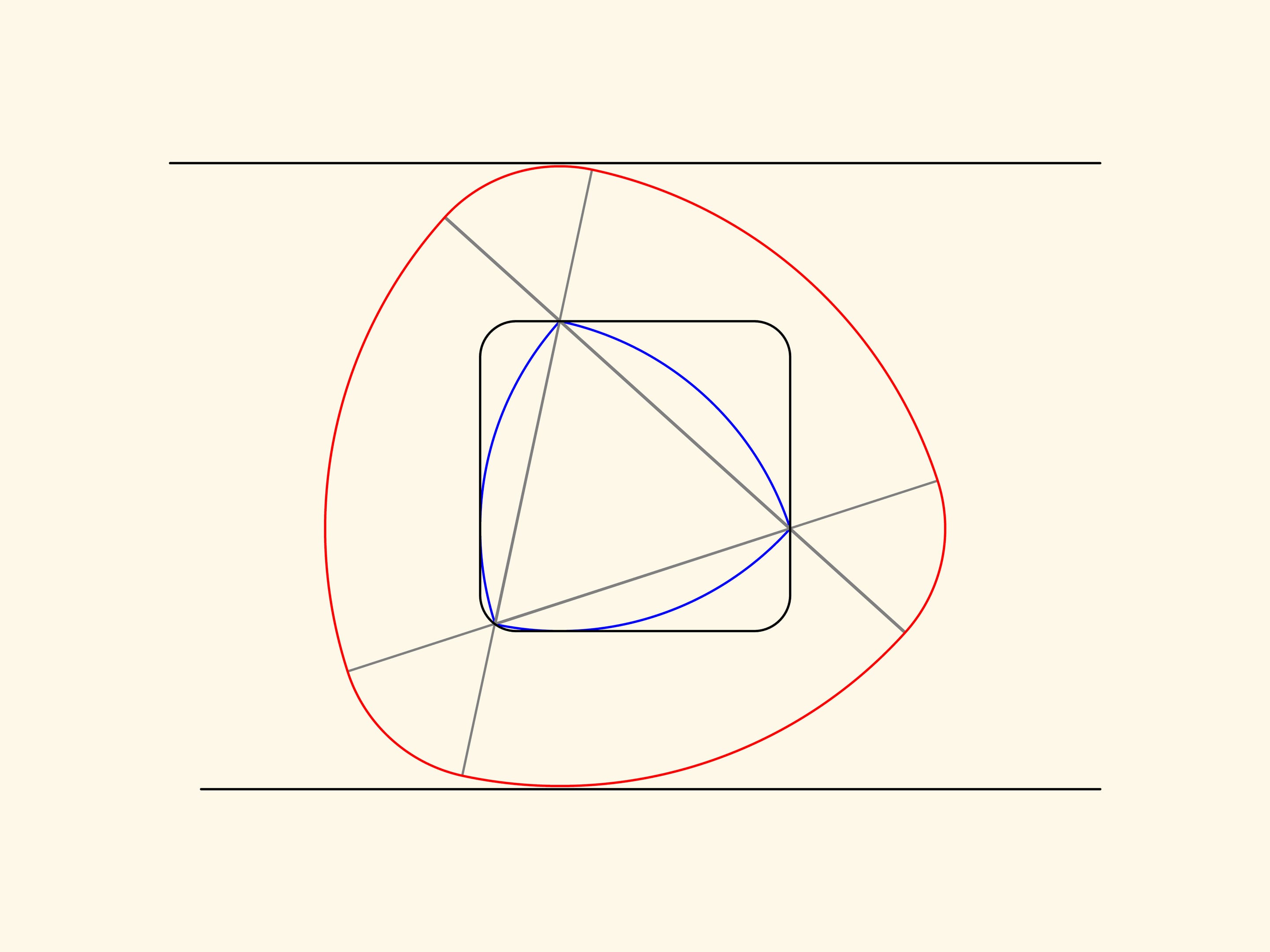
Prolon­geons un des côtés en ajou­tant à ses sommets deux segments de même longueur. Tour­nons le côté ainsi prolongé autour d’un des sommets, jusqu’il recouvre le côté adja­cent. Les arcs de cercles, l’un plus grand et l’autre plus petit, décrits par les extré­mités du côté prolongé, déli­mitent la figure de largeur constante que nous allons construire. Main­te­nant nous faisons tourner le côté prolongé autour de l’autre sommet, et en fin autour du troi­sième sommet.

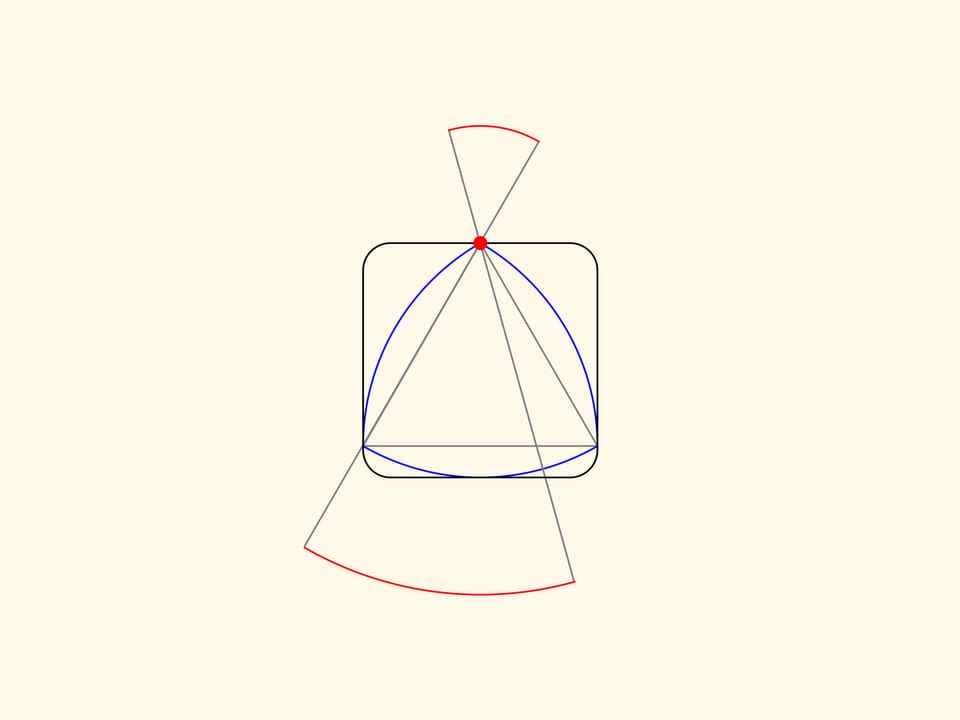
La courbe rouge ainsi obtenue sera composée de trois arcs de grand rayon et de trois arcs de rayon plus petit. On peut démon­trer que cette courbe borne une figure de largeur constante. Peu importe combien les côtés du triangle sont étirés, il est impor­tant que les segments ajoutés ont la même longueur.

Si main­te­nant on fait tourner le triangle de Reuleaux dans le carré, alors la courbe rouge corres­pon­dante tour­nera entre deux droites paral­lèles, qui ne se déplacent pas par rapport au carré.

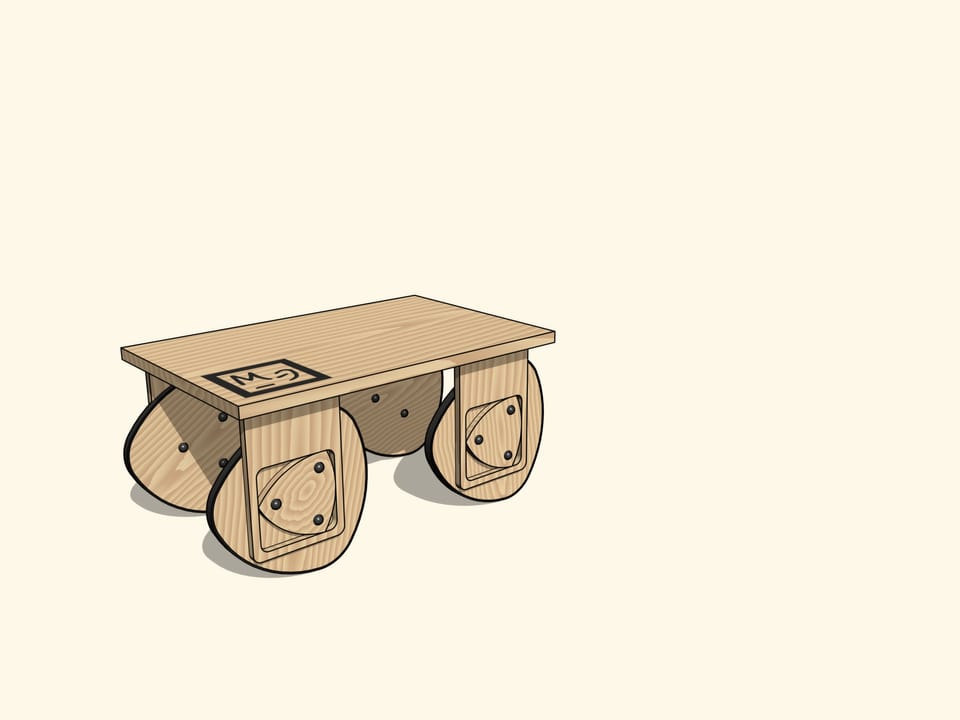
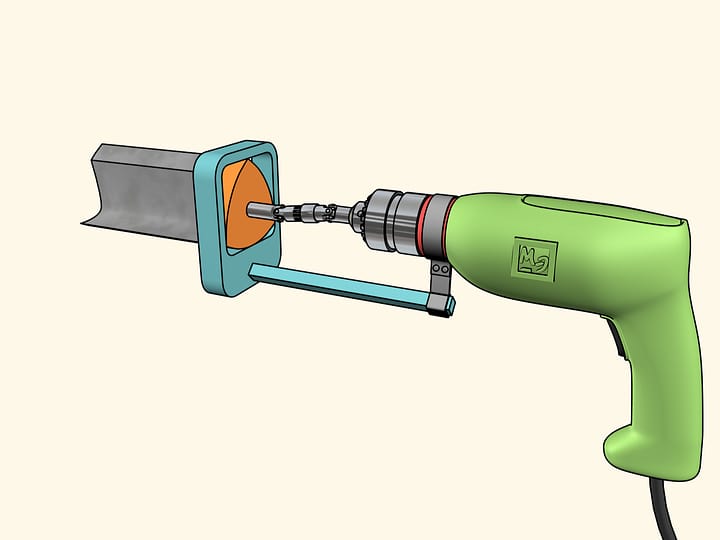
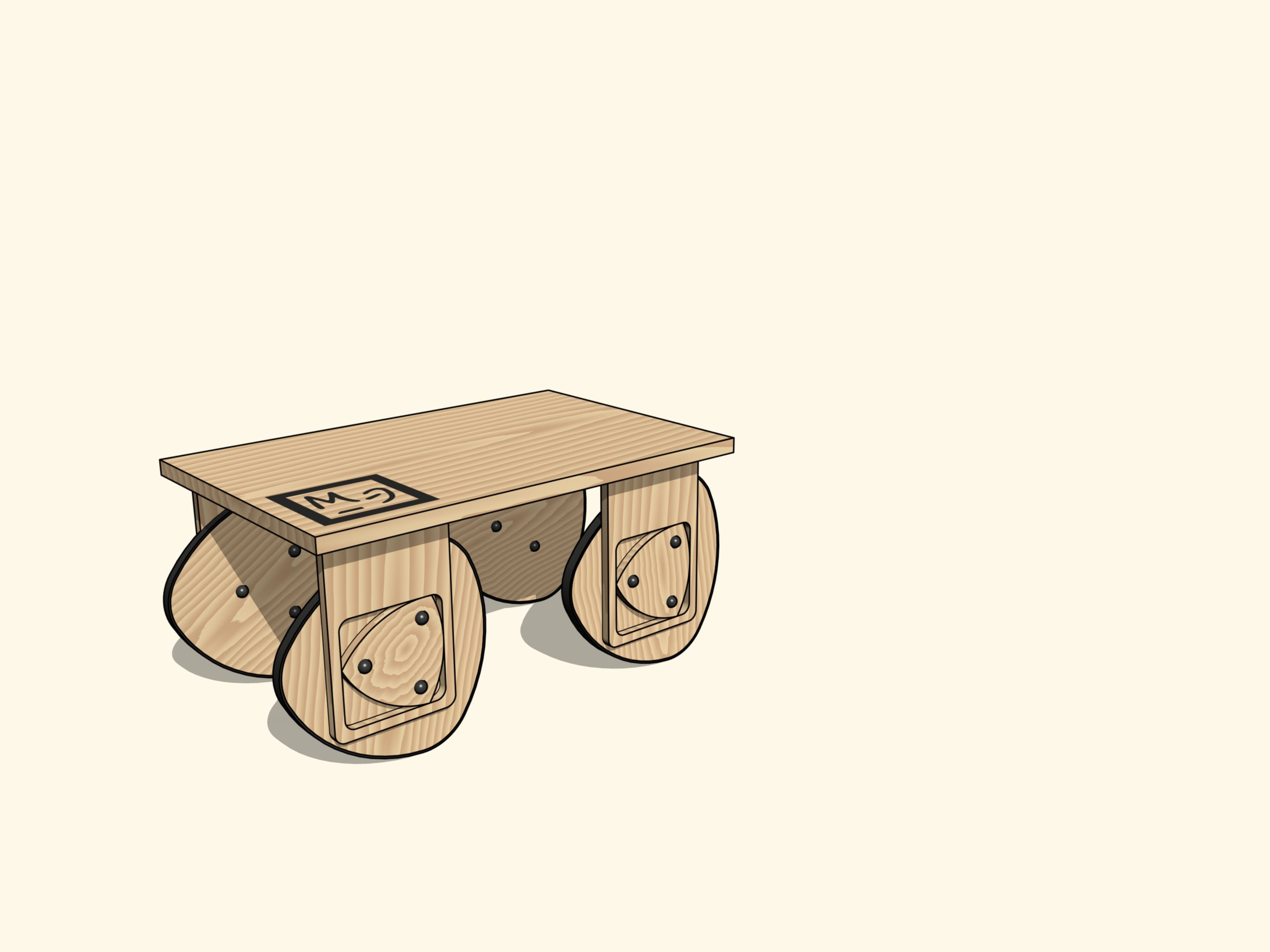
En conséquence, nous pouvons construire un chariot avec des roues non circu­laires, avec le bord ayant la forme de la courbe rouge.

Repo­sant sur quatre suspen­sions de ce genre, notre chariot se déplace abso­lu­ment sans osciller!

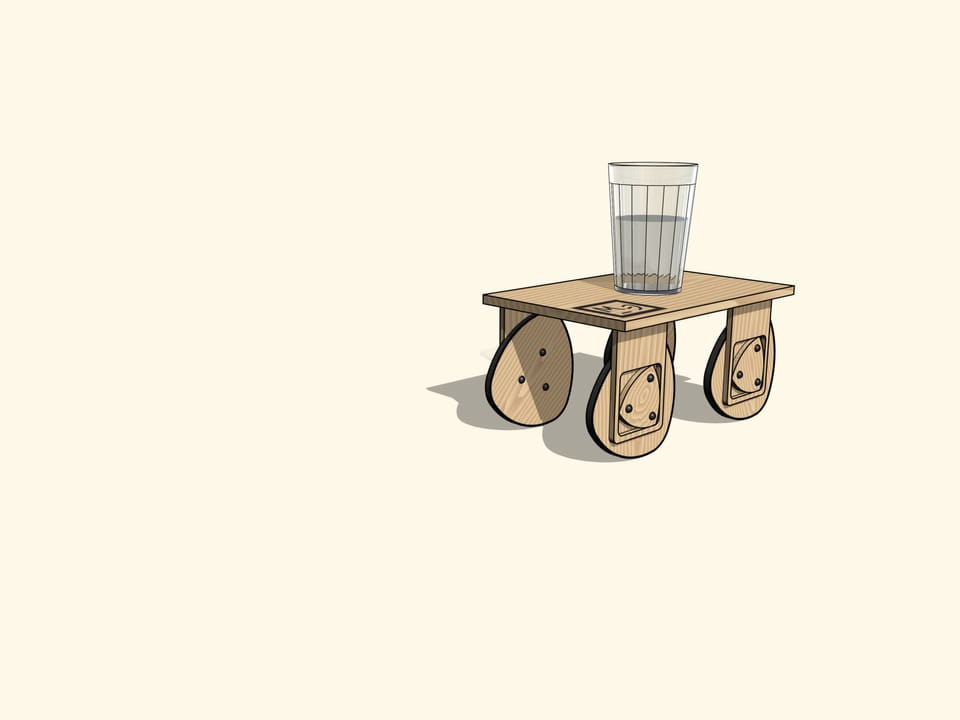
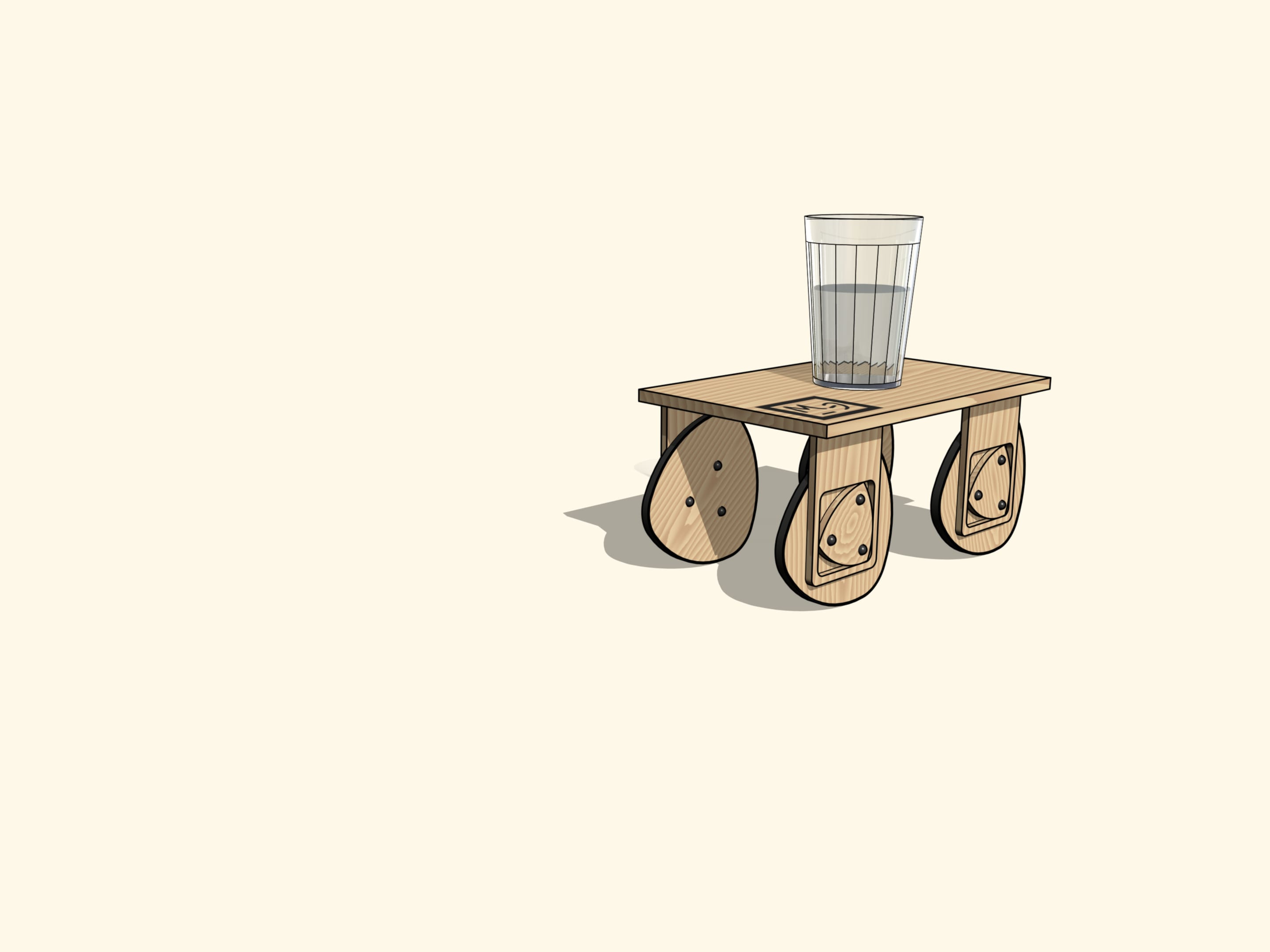
Afin de s’assurer qu’il n’ya pas de secousses, nous avons mis un verre d’eau sur notre chariot comme la tradi­tion auto­mo­bi­lis­tique nous enseigne. La surface lisse de l’eau nous montre encore une fois qu’il y a des roues non–circu­laires avec des suspen­sions spéciales réalisés afin que le chariot se déplace sur eux tout à fait hori­zon­ta­le­ment.