Le problème consiste à diviser un angle en trois parties égales. Avec deux autres problèmes classiques de construction — la duplication du cube et la quadrature du cercle — le problème de la trisection est venu jusqu’à nous de la Grèce antique et dans le cours de plusieurs siècles a occupé les esprits de meilleurs mathématiciens.
On a essayé plusieurs fois de résoudre ces problèmes en faisant usage des instruments sacrés de la géométrie euclidienne: la règle et le compas.Entre autres choses, même dans l’antiquité les mathématiciens avaient deviné que, en utilisant la règle et le compas seuls, ces problèmes étaient insurmontables, mais plus tard, cela fut démontré. Les tentatives visant à élargir la gamme des outils permis eu une grande influence sur les mathématiques de la Grèce antique, et a mené à la première étude des sections coniques, à la recherche de courbes complexes, et à la construction de théories intéressants.
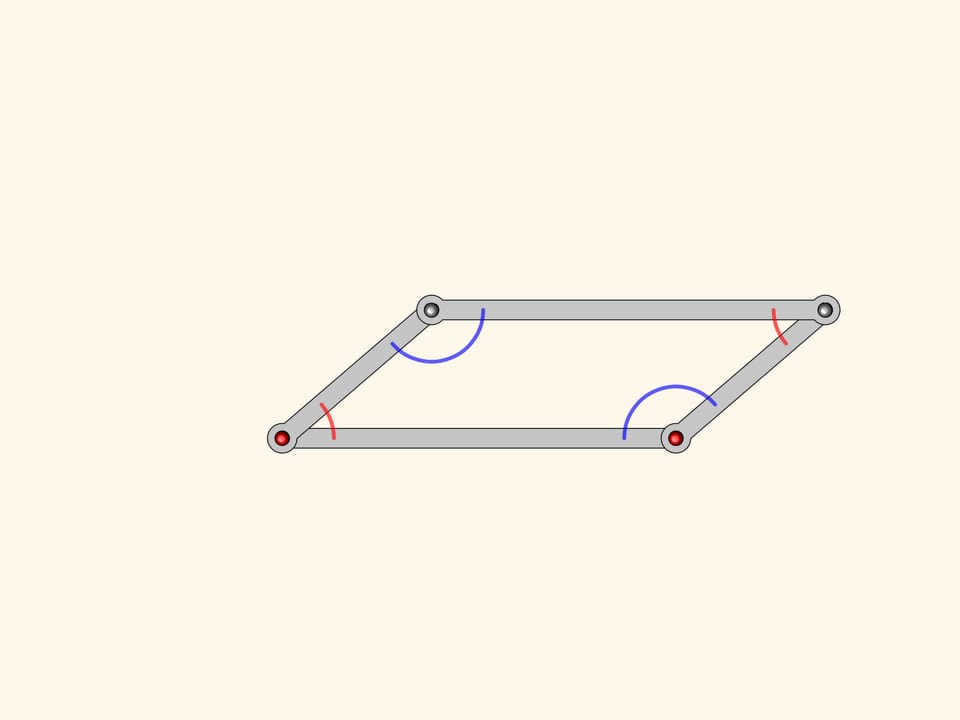
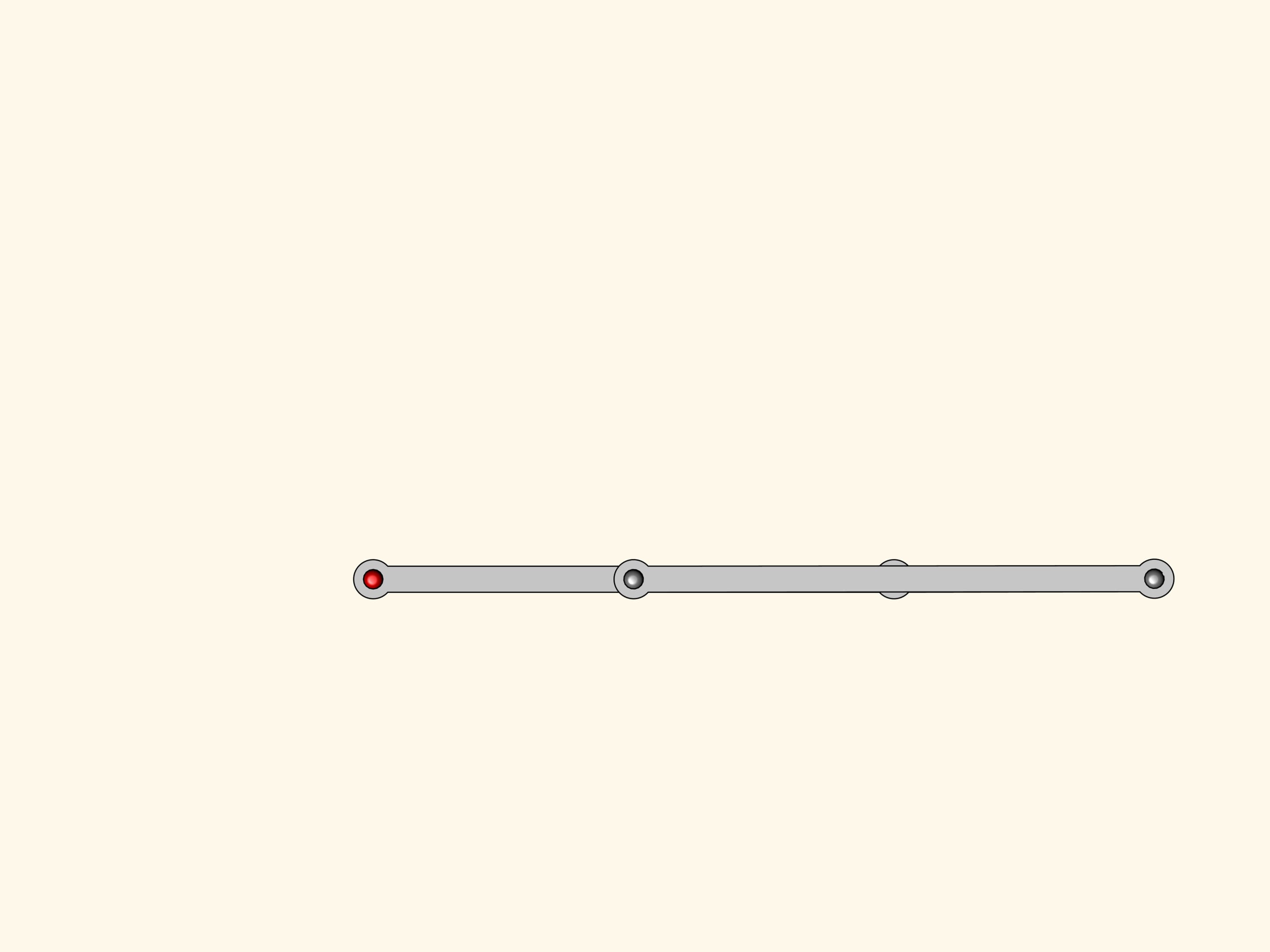
Considérons un mécanisme à charnières, composée d’un parallélogramme avec deux charnières fixes. Du cours de mathématiques à l’école vous vous souviendrez que les angles opposés d’un parallélogramme sont égaux. Cela est vrai pour tout parallélogramme, et donc aussi pour notre mécanisme, n’importe comment soit–il incliné.
Mais vraiment n’importe comment ?
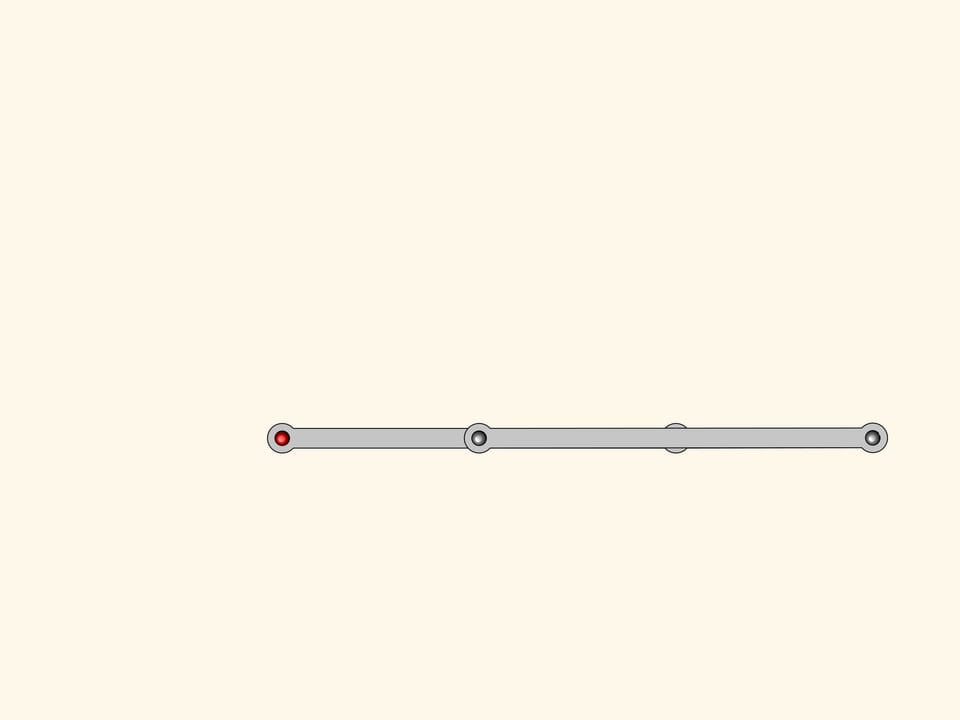
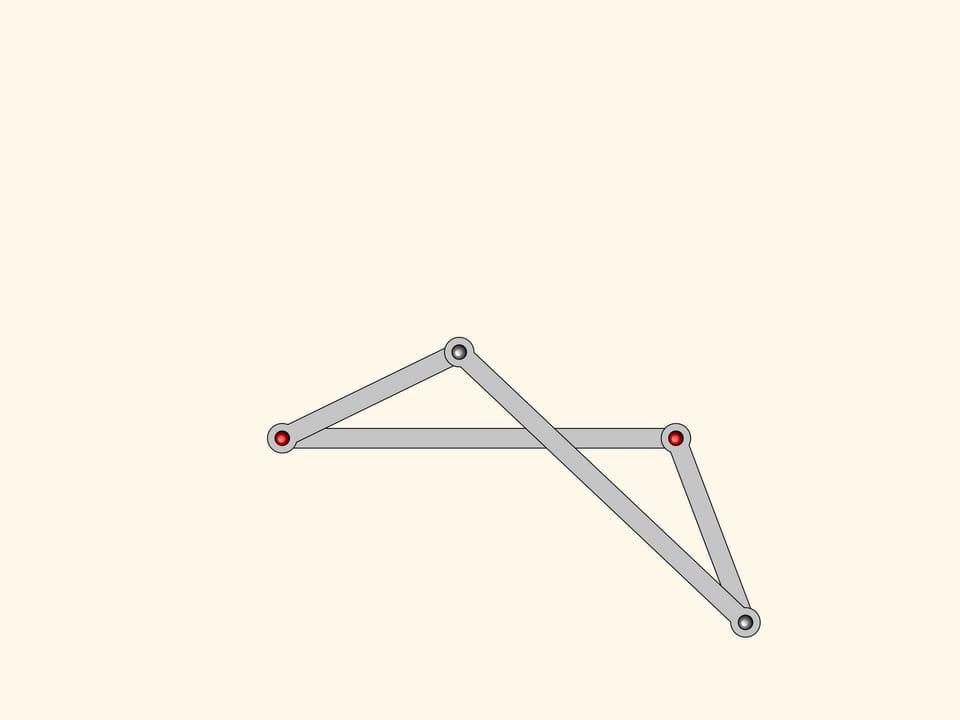
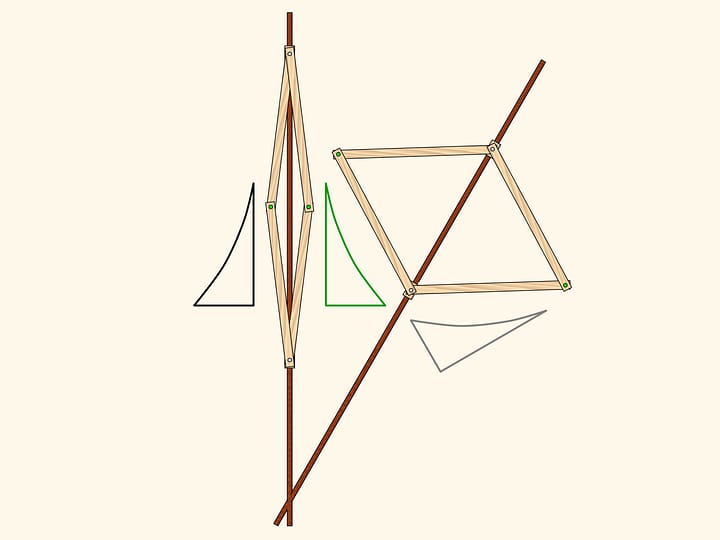
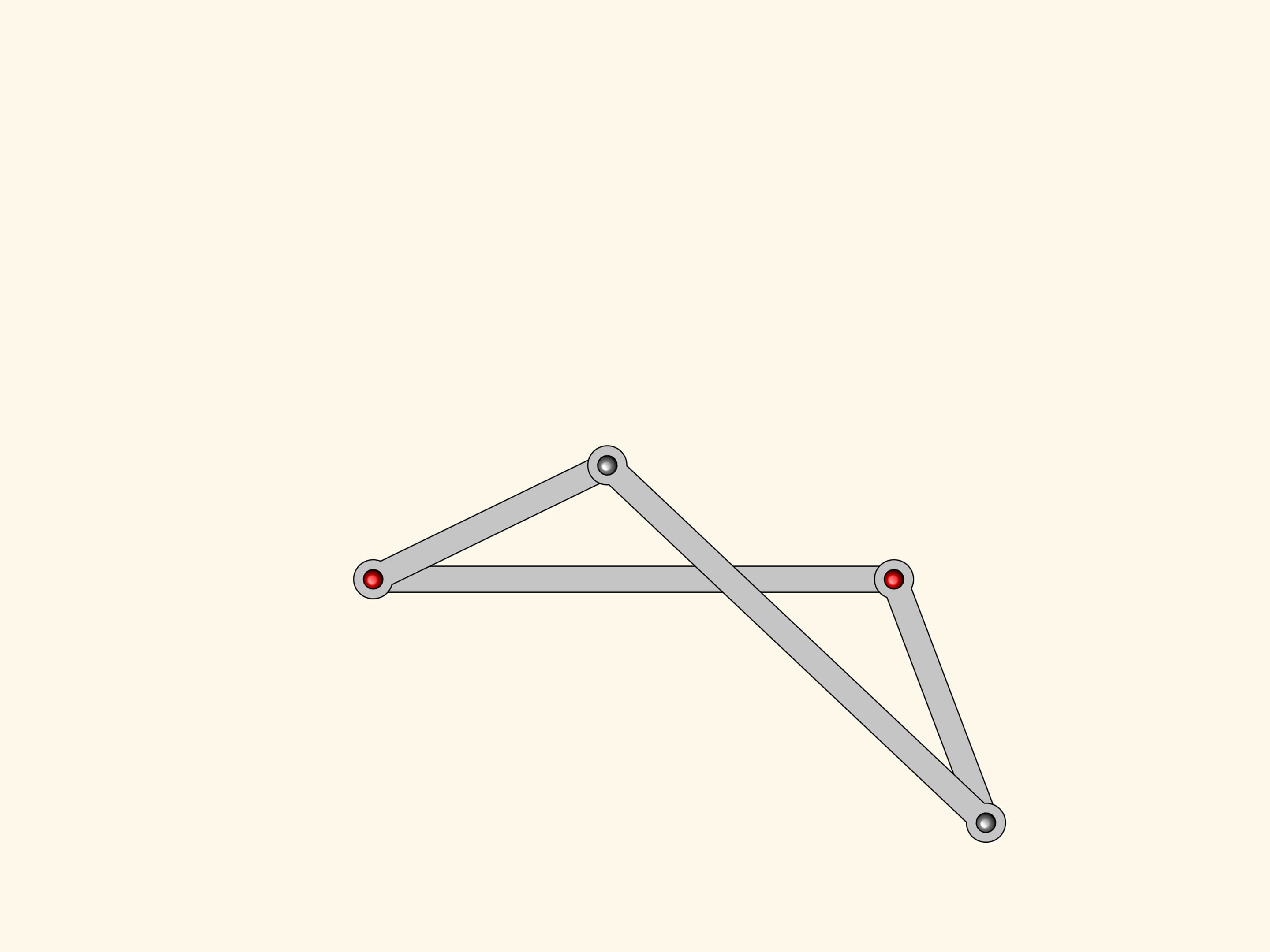
Notre système a un point singulier, lorsque toutes les barres sont sur la même ligne. De ce point de bifurcation le mécanisme peut sortir ou redevenant un parallélogramme ou se transformant en une figure appelée antiparallélogramme.
Alfred Bray Kempe 1849—1922
C’est cette singularité du mécanisme à charnières que nous avons considéré qui a été la cause d’une erreur dans le raisonnement d’Alfred Kempe ; en 1876 il «prouva» le théorème qu’il ya un mécanisme à charnières, capable de forger votre signature et ne pouvant dessiner rien d’autre. Plus précisément, que toute courbe algébrique qui est dans une région bornée du plan est la trajectoire d’un mécanisme planaire à charnières. Le théorème lui–même est vrai, mais seulement en 1984 on a trouvé qu’il n’y avait une erreur dans la preuve de Kempe et seulement à la fin du XXe siècle on l’a corrigé.
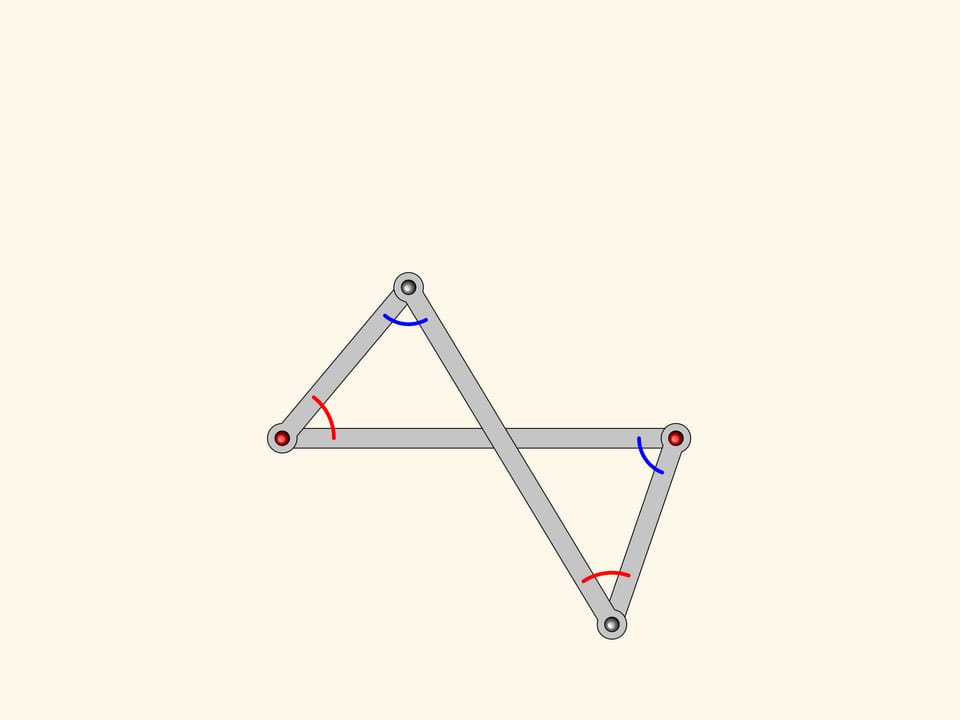
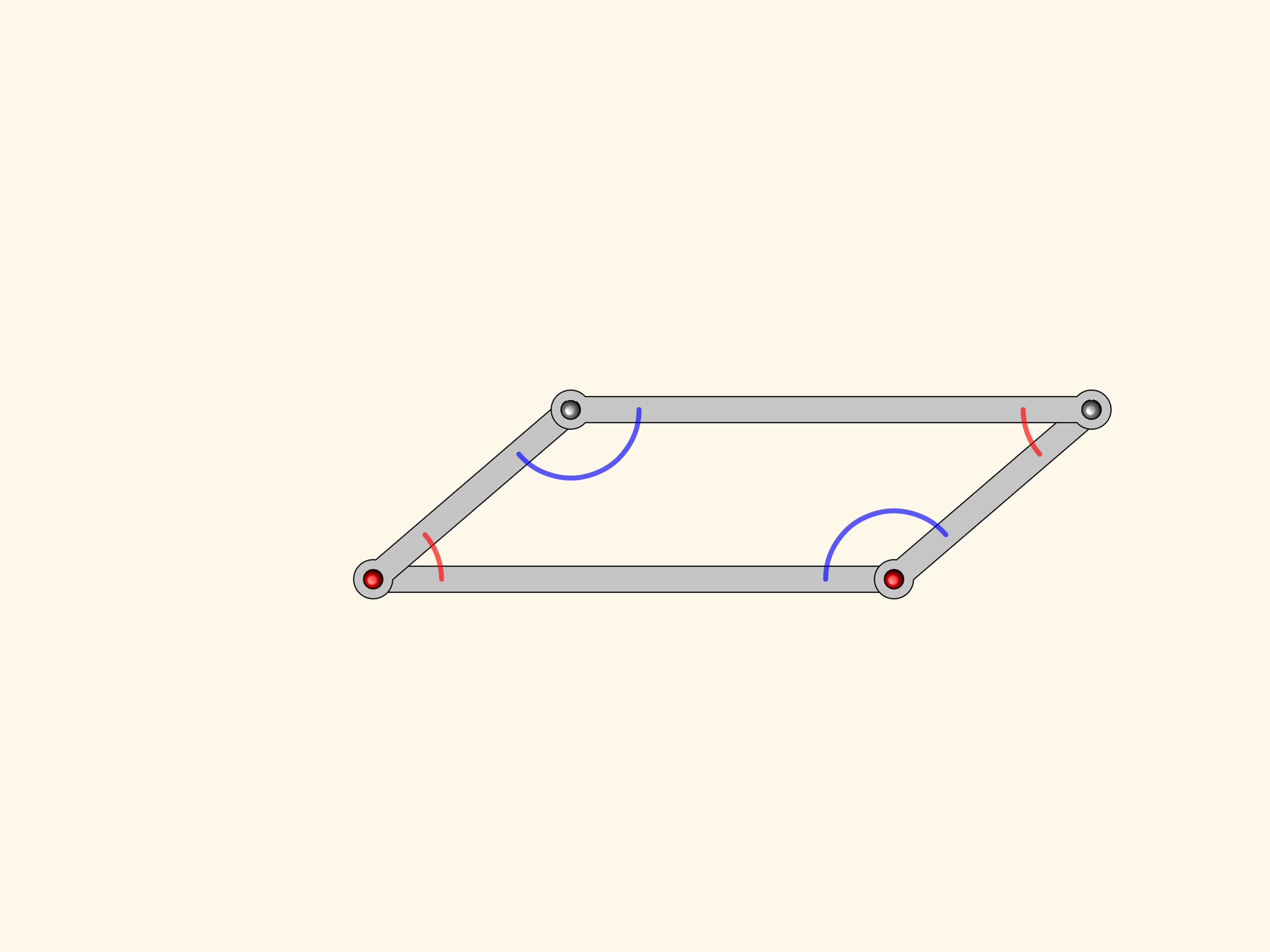
Du parallélogramme l’antiparallélogramme hérite la propriété que les deux côtés opposés sont égaux ; même les deux autres, qui se croisent entre eux, sont égaux. Mais notre figure possède également une relation entre les angles: même dans l’antiparallélogramme ils sont égaux en couple!
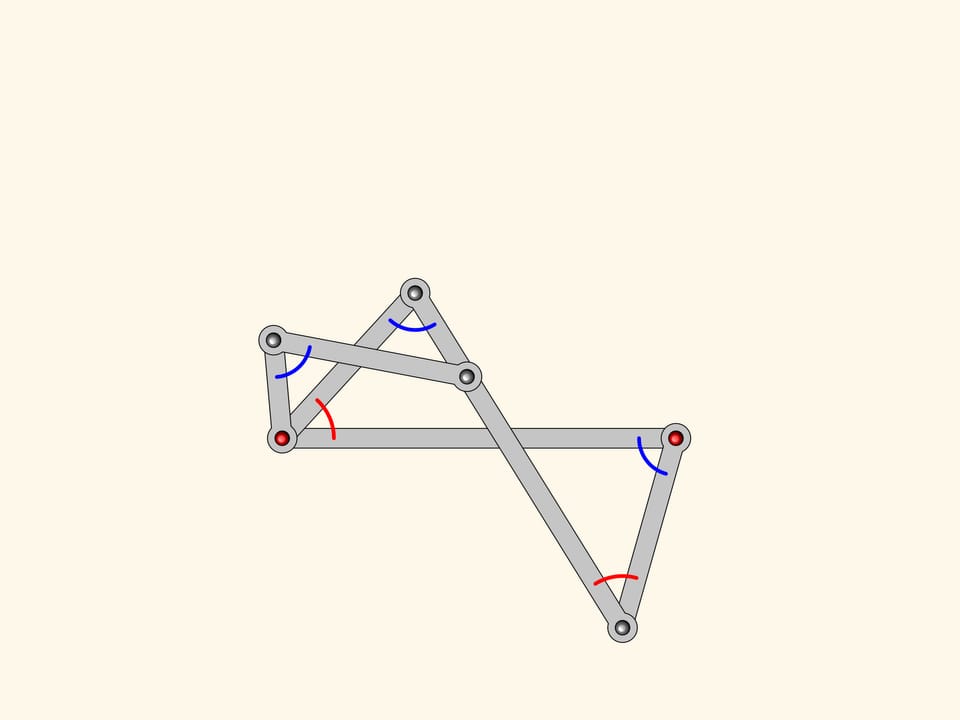
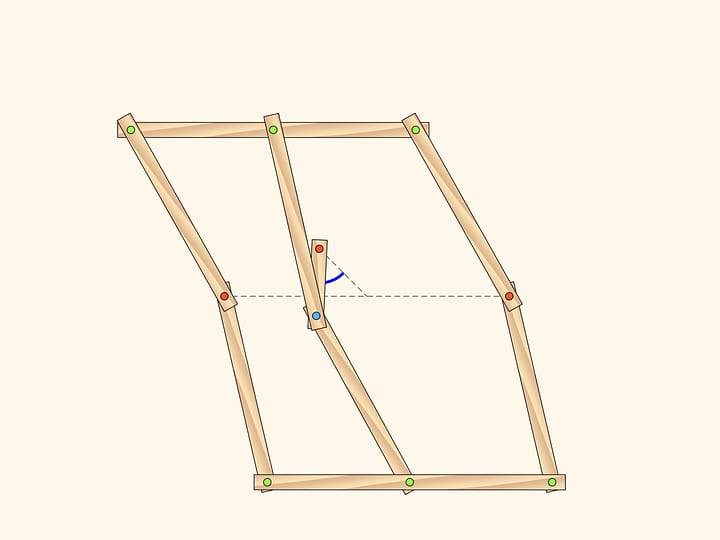
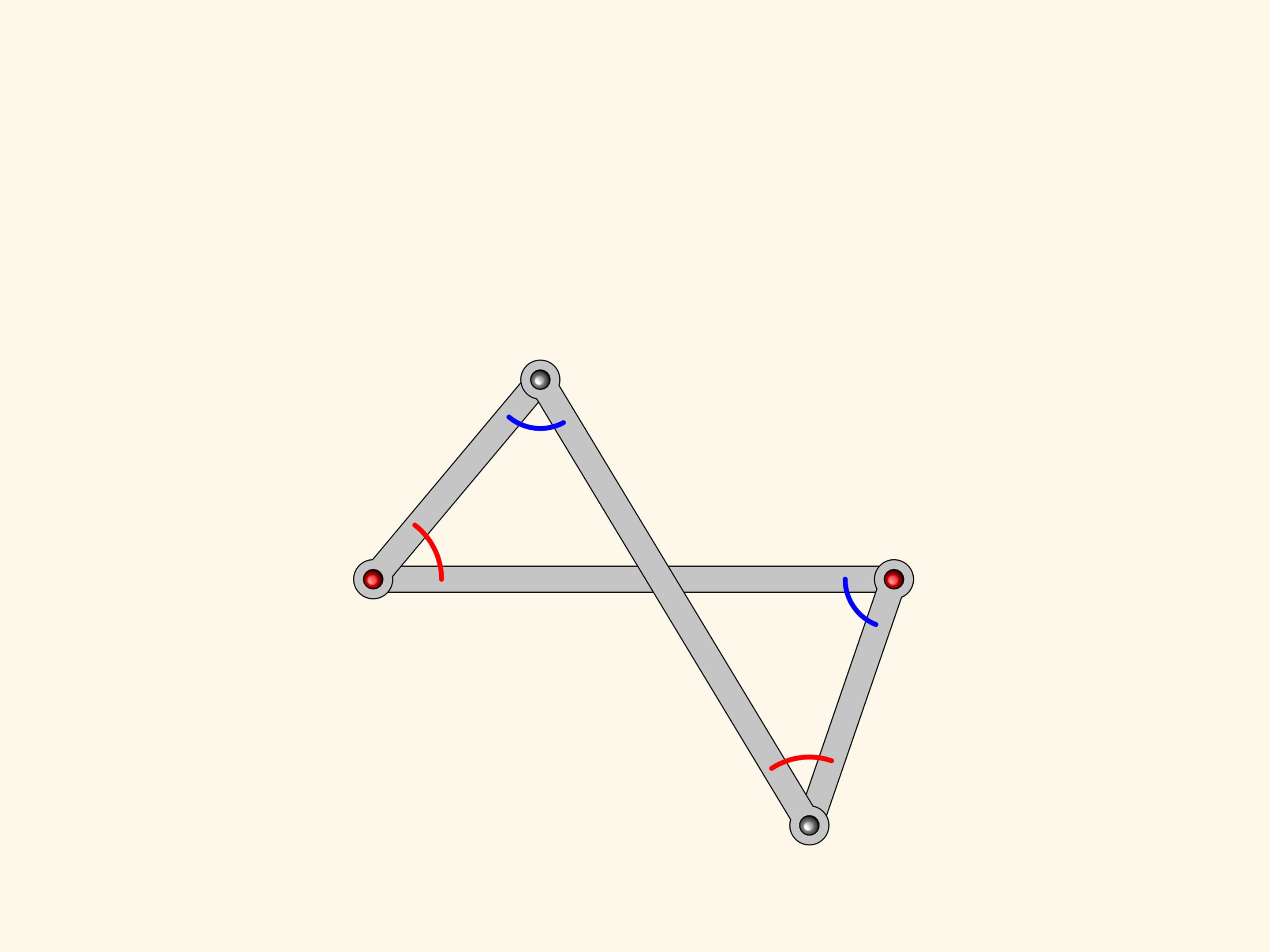
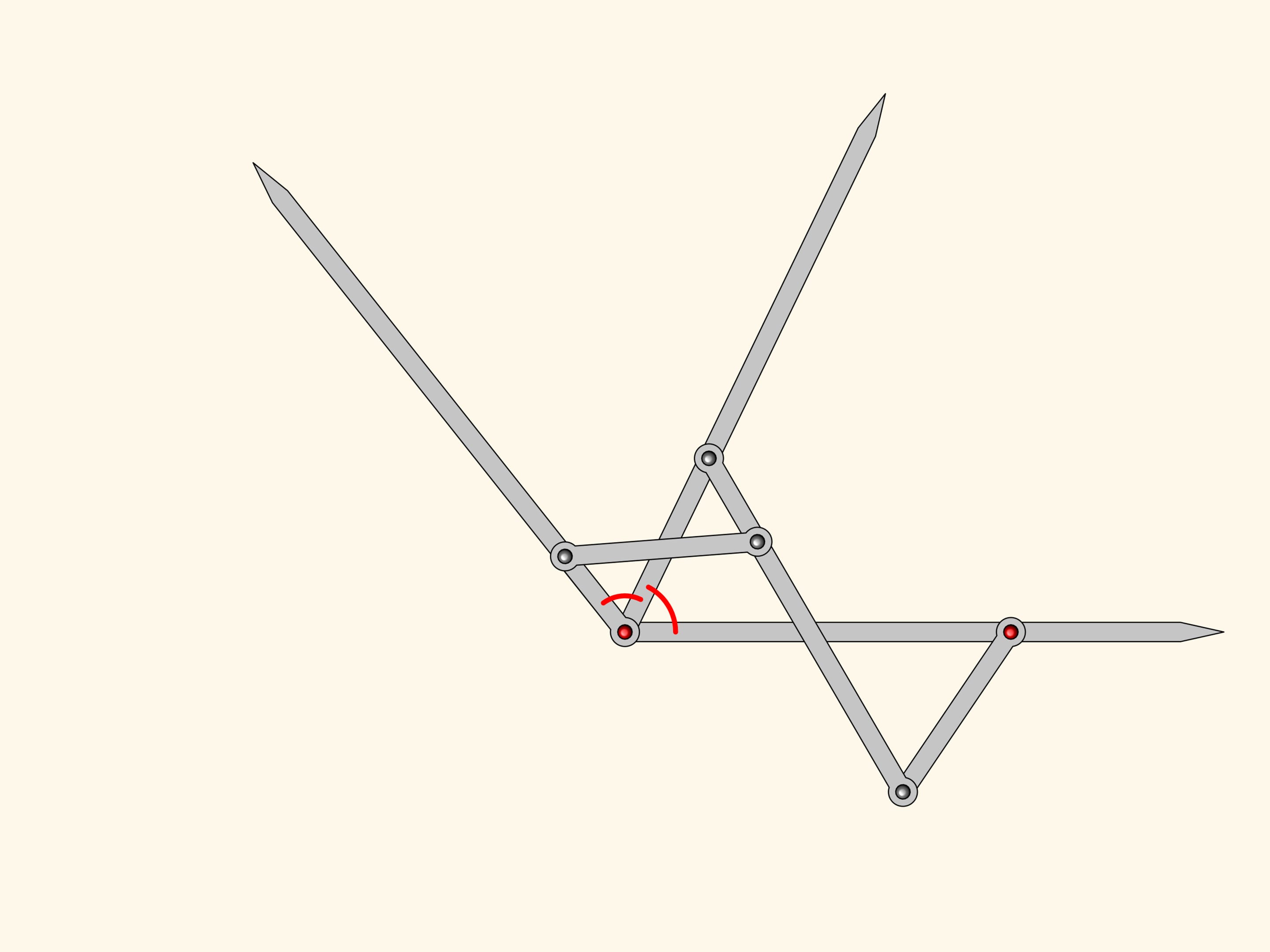
Ajoutons à notre antiparallélogramme un autre antiparallélogramme plus petit, mais semblable au premier. Ils ont un angle en commun, ce qui signifie que les angles marqués en rouge sont les mêmes.
En étendant les côtés de ces angles, on obtient un mécanisme planaire à charnières qui peut être utilisé pour construire la bissectrice d’un angle quelconque.
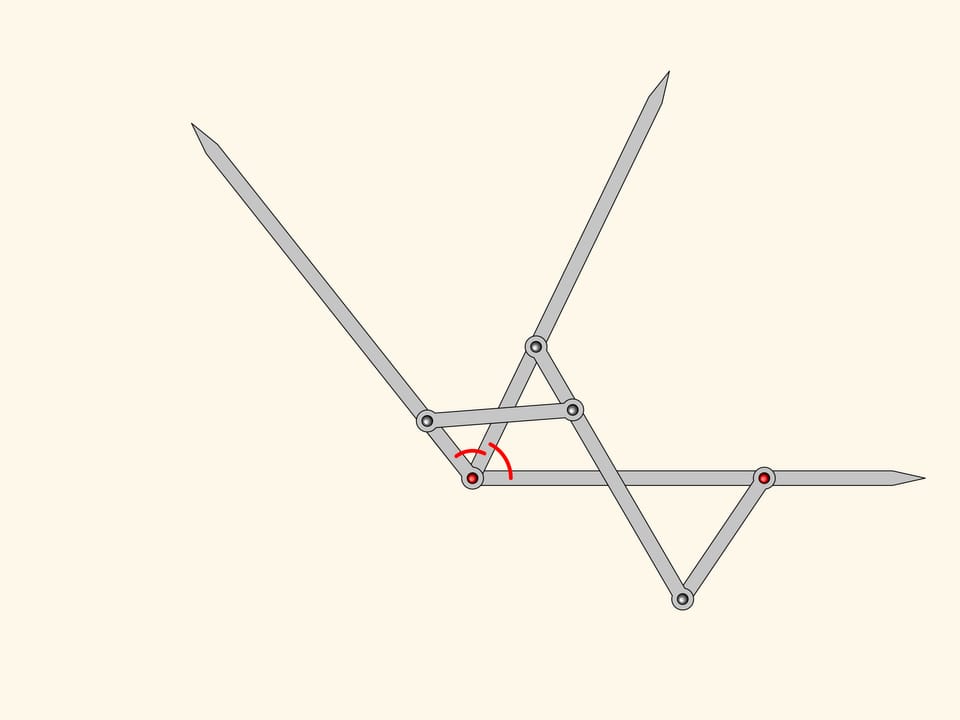
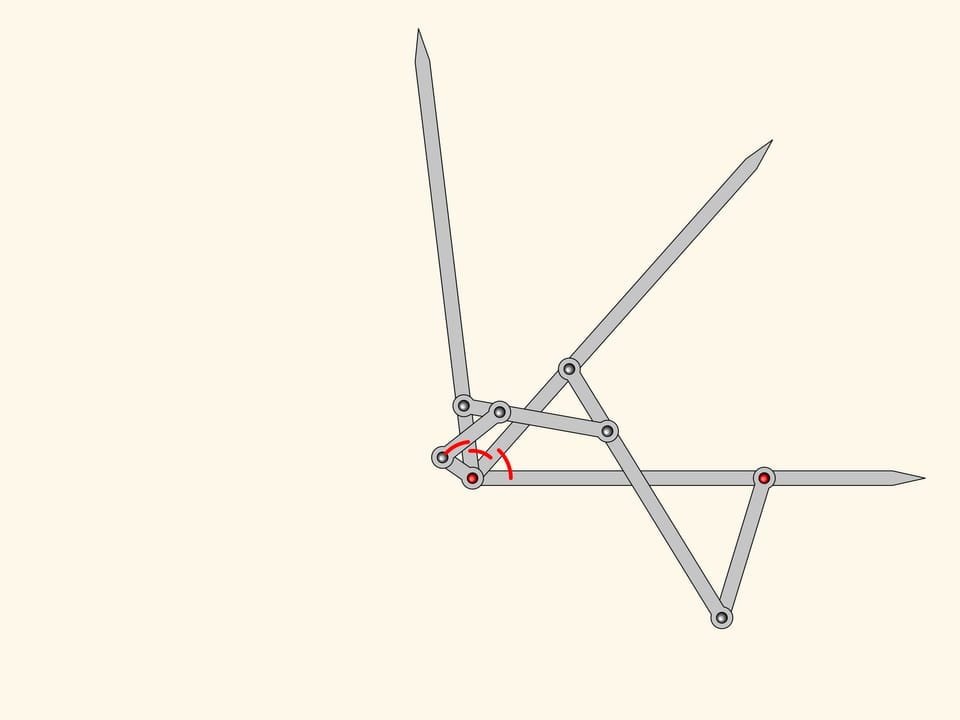
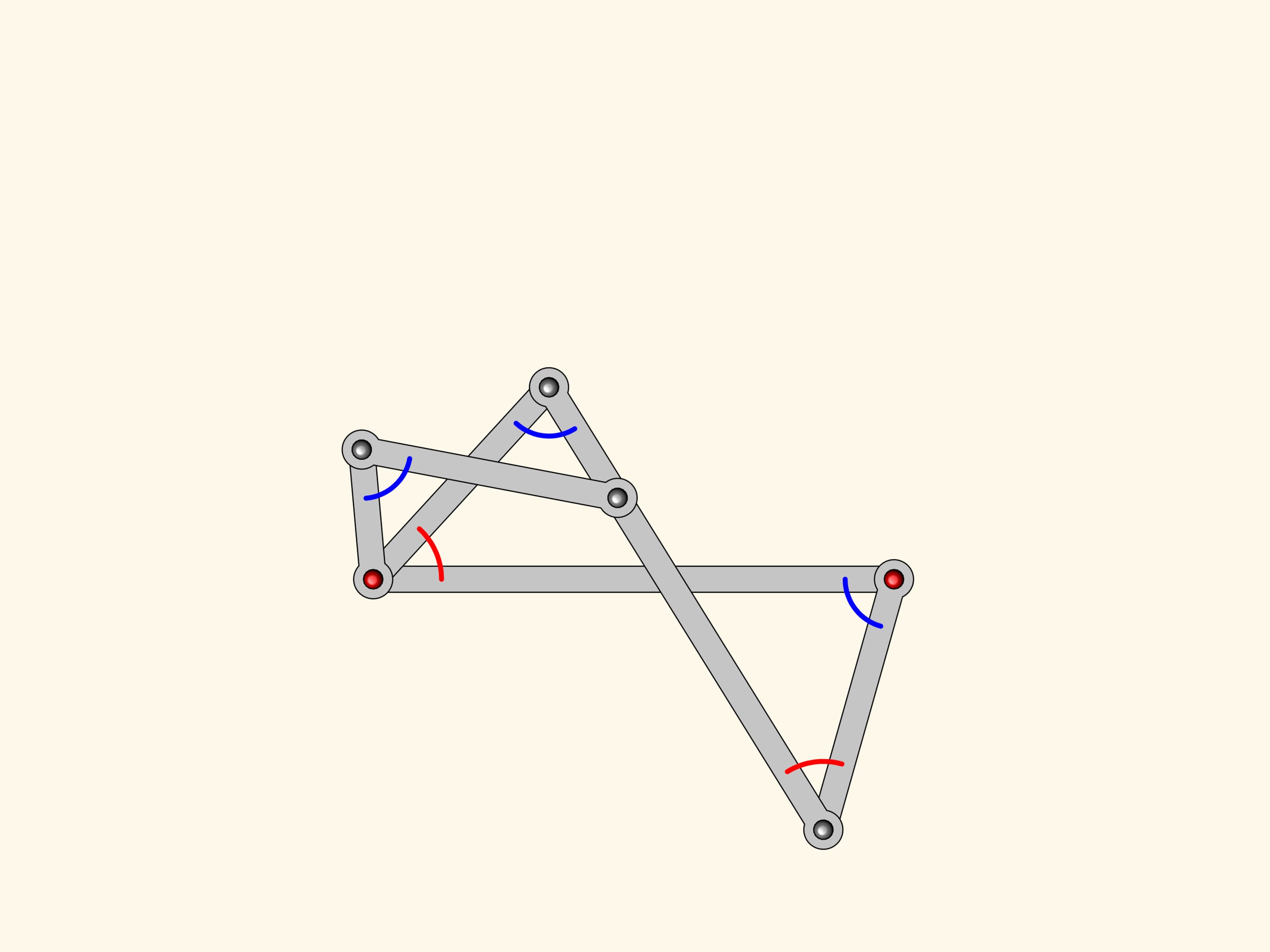
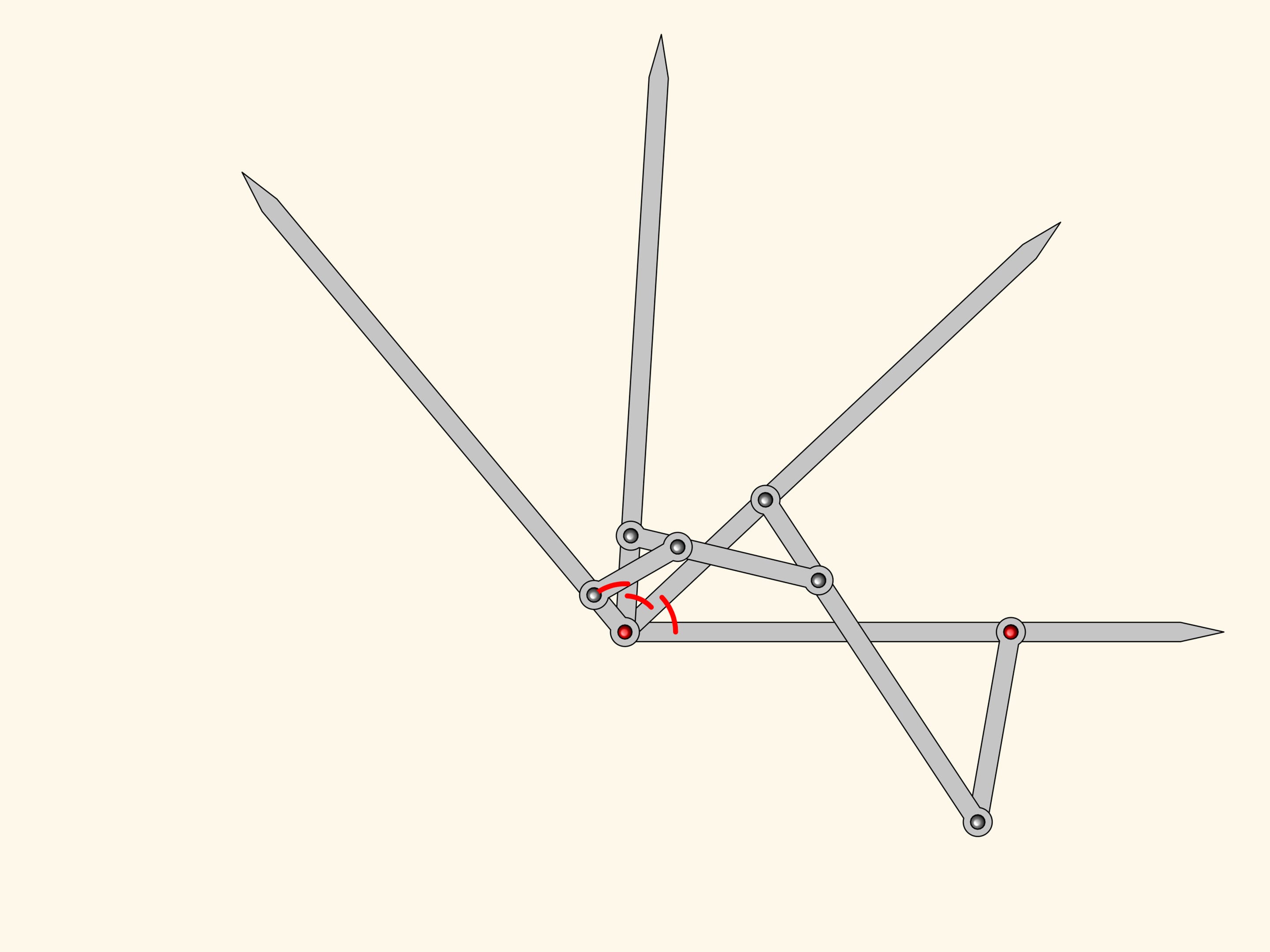
Nous pouvons maintenant ajouter encore un autre antiparallélogramme semblable aux deux premiers. Avec le même raisonnement, l’angle près de la charnière en rouge sera égal aux deux autres voisins, que nous avons déjà montré être égaux.
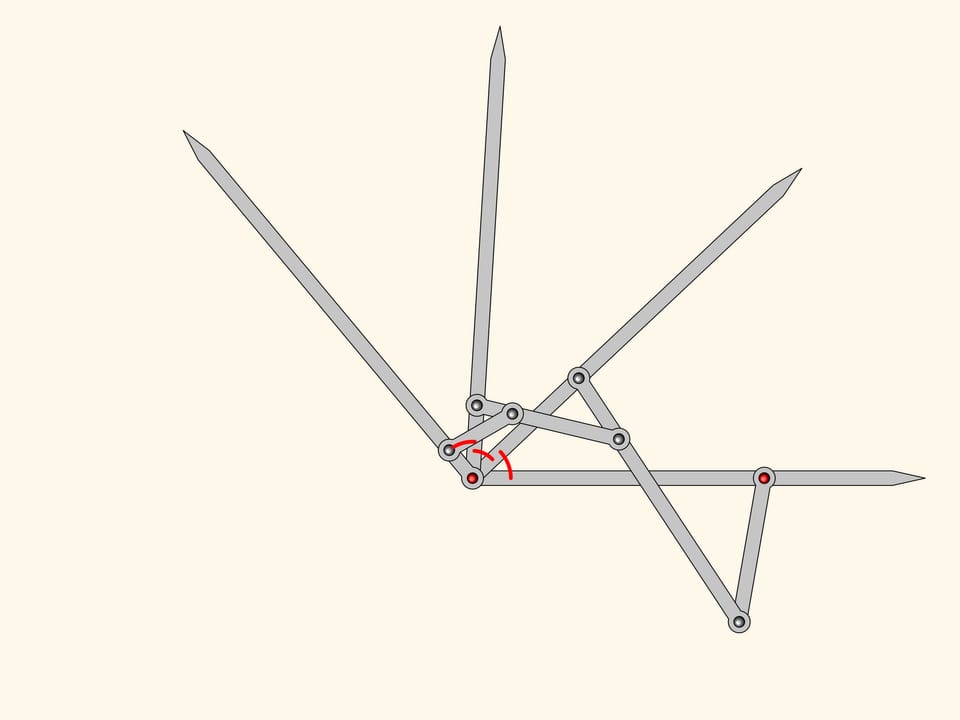
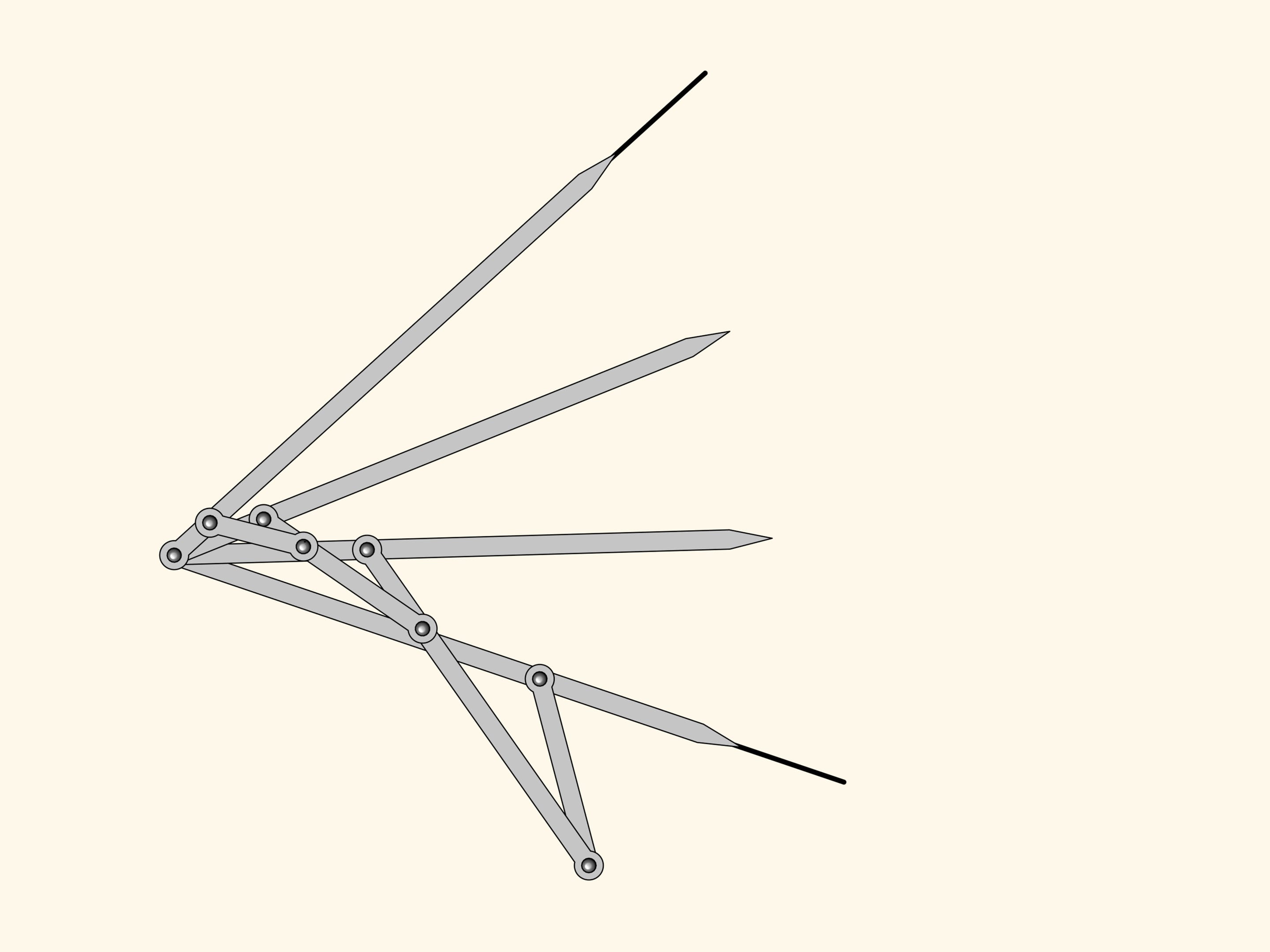
Le mécanisme planaire à charnières que nous avons obtenu est un trisecteur d’angles, et pourtant il résout le problème de la division de n’importe quel angle en trois parties égales!
Kempe s’arrêta sur ce mécanisme, puisque dans sa «preuve» du théorème de la «signature» il lui fallait un mécanisme capable de diviser un angle dans exactement trois parties. Cependant, il est clair qu’on peut encore continuer l’algorithme de construction du trisecteur, et ainsi obtenir des mécanismes à charnières qui divisent n’importe quel angle dans un nombre arbitraire de parties égales.