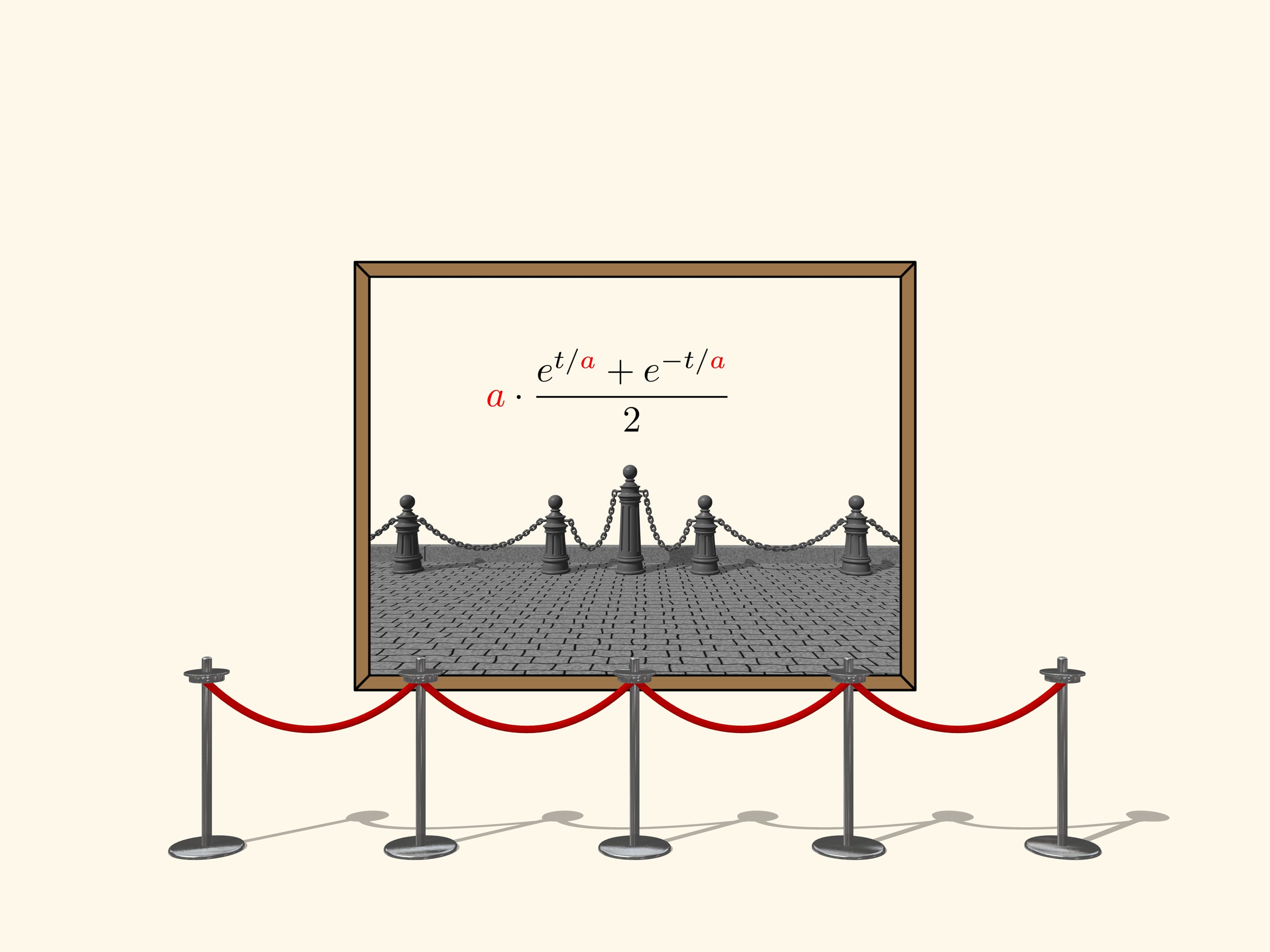
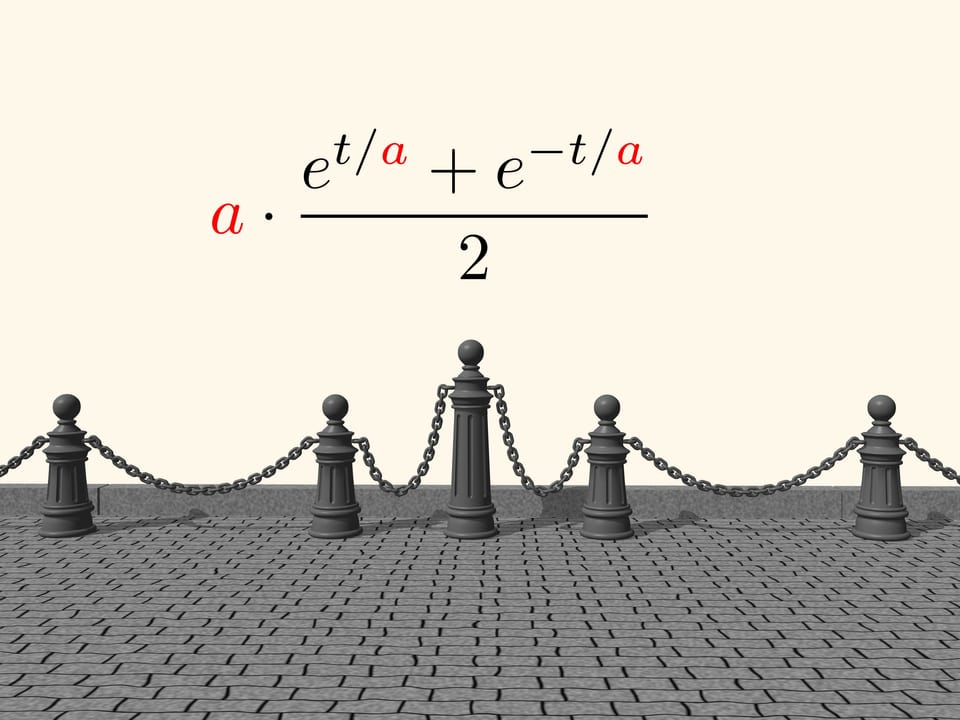... Une autre façon de tracer la parabole cherchée sur un mur est la suivante. Plantons deux clous dans le mur à la même hauteur au-dessus de l'horizon, à une distance l'un de l'autre, qui est le double de la largeur du rectangle, où nous voulons inscrire la parabole. Accrochez aux clous les extrémités d'une chaîne fine d'une longueur telle que son point le plus bas se trouve à une distance du niveau des clous égale à la hauteur du rectangle. La chaîne suspendue prend la forme d'une parabole, de sorte que, en marquant les points du mur par les maillons de la chaîne, on obtient le tracé d'une parabole, qui est bissecté par le segment de droite perpendiculaire qui passe entre les deux clous en son point médian.
Galileo Galilei “Conversations et preuves mathématiques.” 1638.
Cependant, le mètre s’est trompé. Il y aura une petite distinction entre une parabole et une ligne de chaîne courbe. A peine un demi-siècle plus tard, Yoan Bernulli, Godfried Leibnitz et Christian Hughens ont déduit l’équation de la “Chaînette”. Un paramètre la compose,et, en le modifiant, il peut recevoir une diversité de fléchissements courbes de chaîne. Nous devons l’origine du nom “Chaînette” à Hughens.
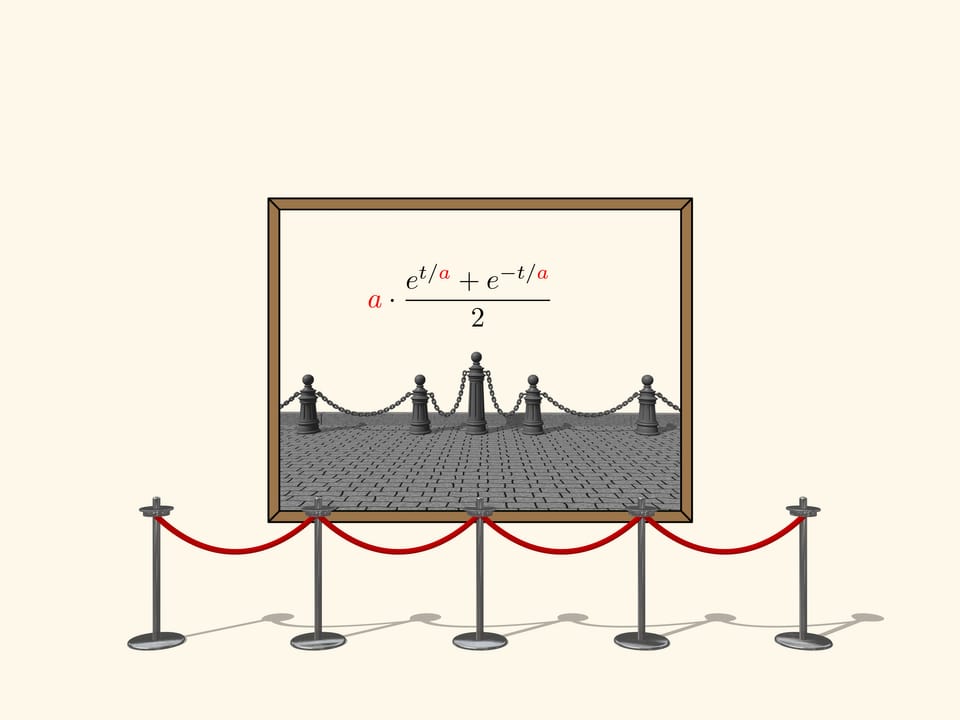
Il n’y a pas seulement une chaîne suspendue le long de cette ligne, mais n’importe qu’elle autre fil similaire non tendu par l’action de la force de pesanteur. Vous pouvez observer cette courbe, par exemple, en visitant un musée.
Mais retournons à notre tableau.
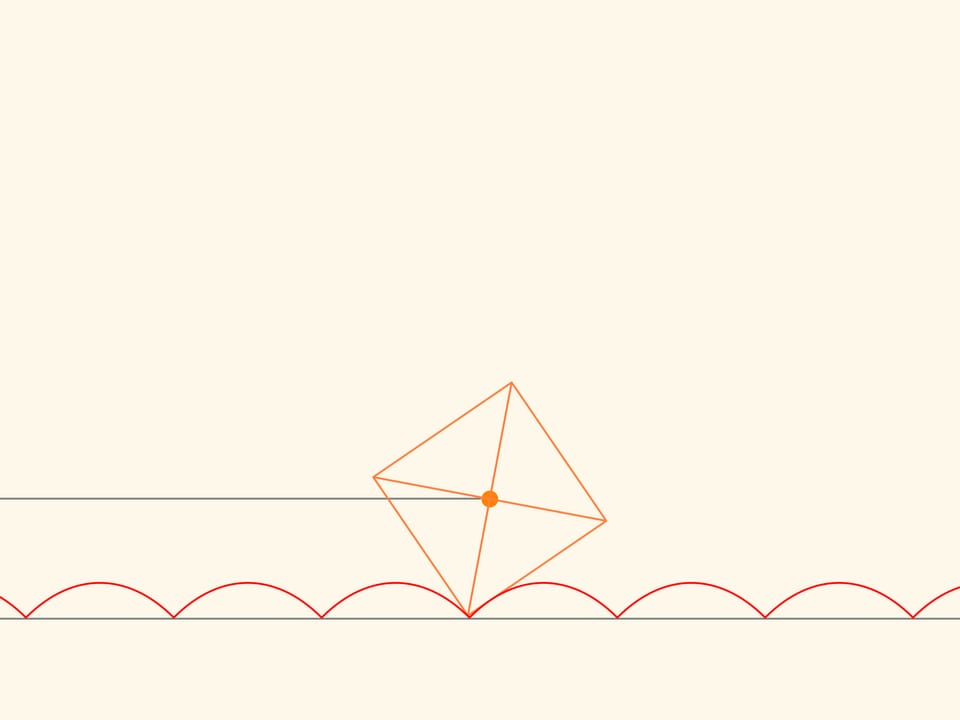
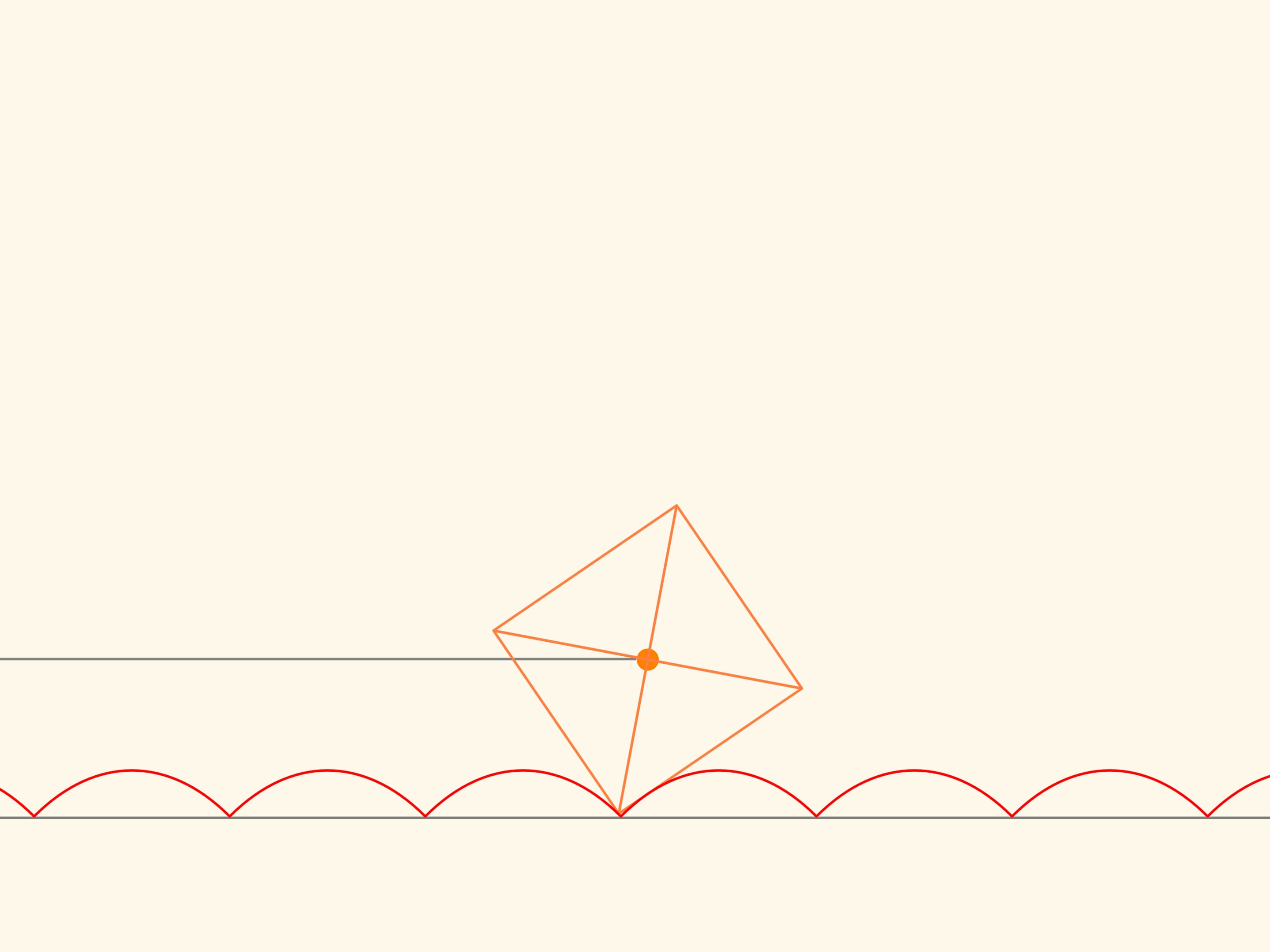
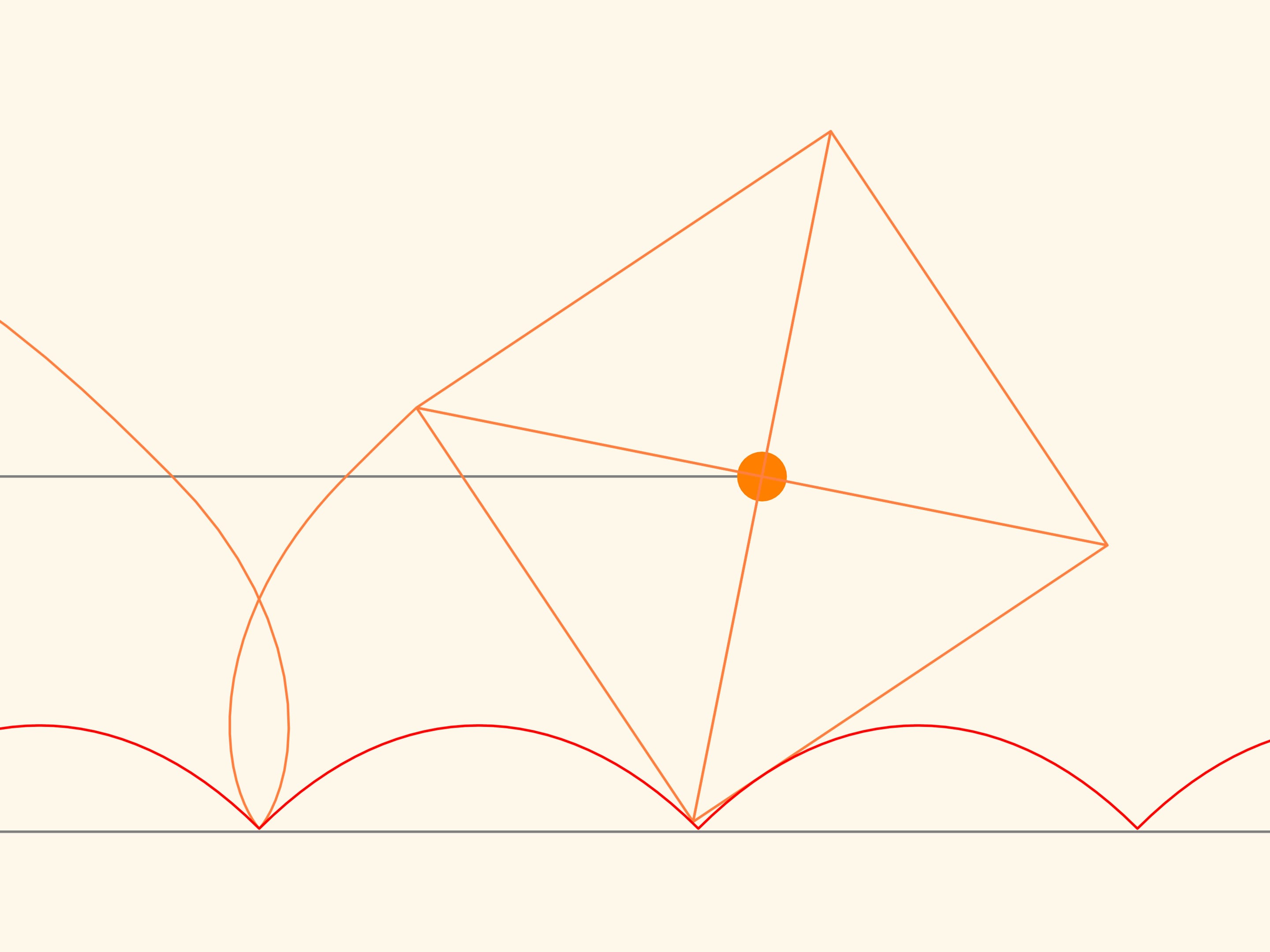
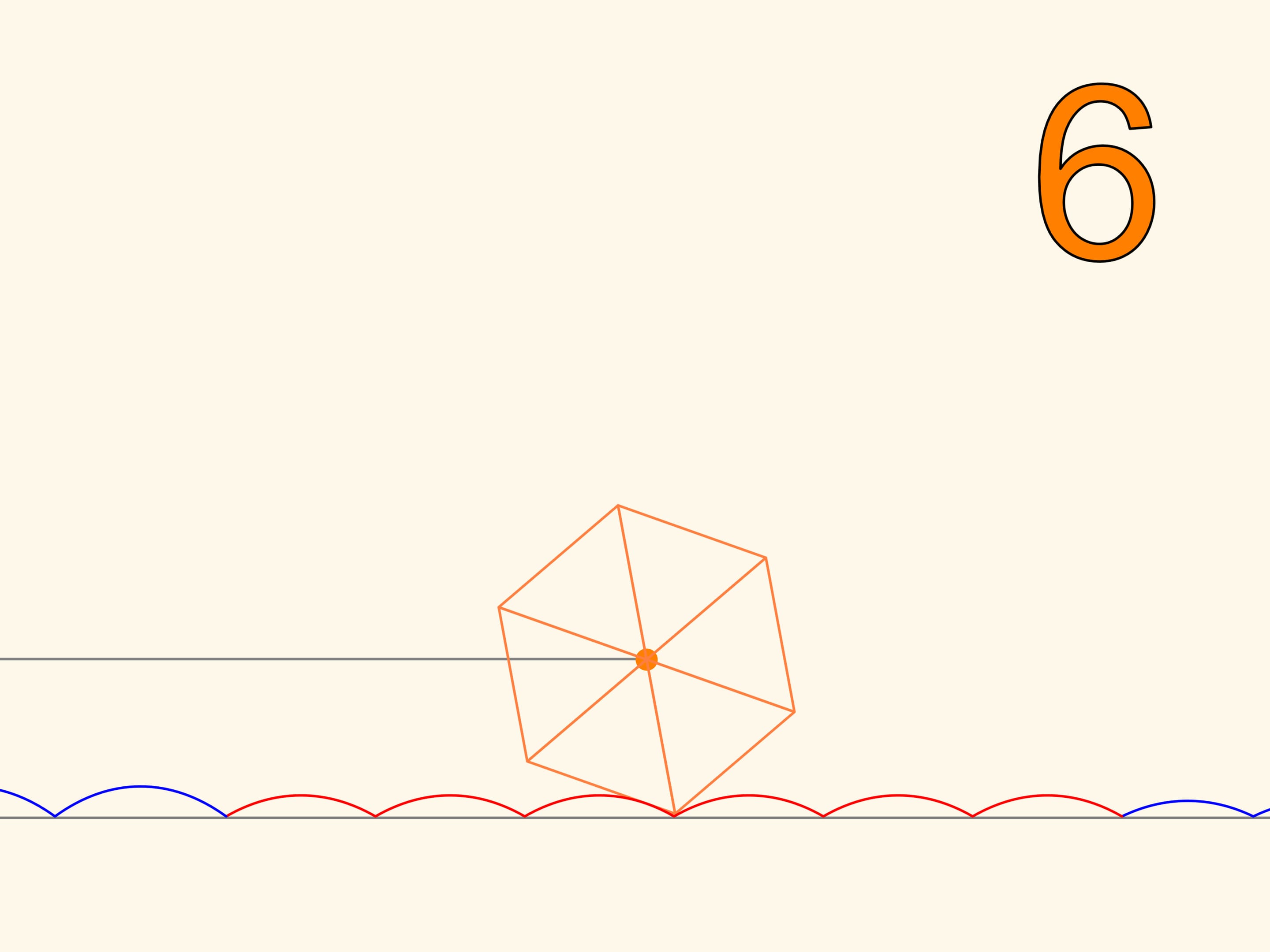
Si on relève un paramètre dans l’équation, comme le centre du carré, se déplaçant sans heurt le long de l’arc de la chaînette, alors, il se déplacera le long d’une droite!
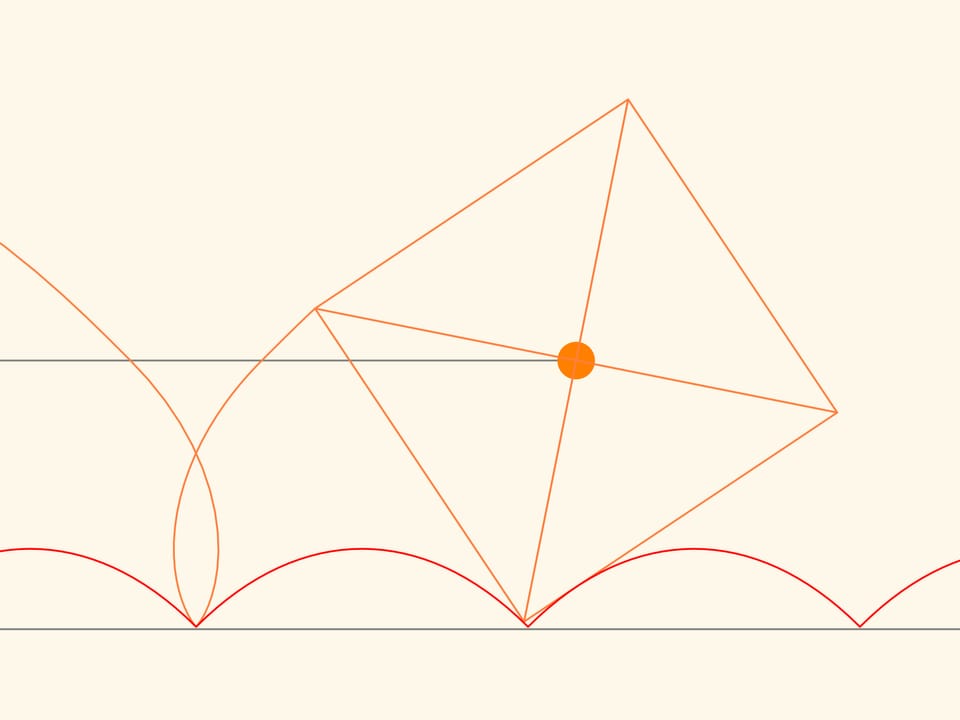
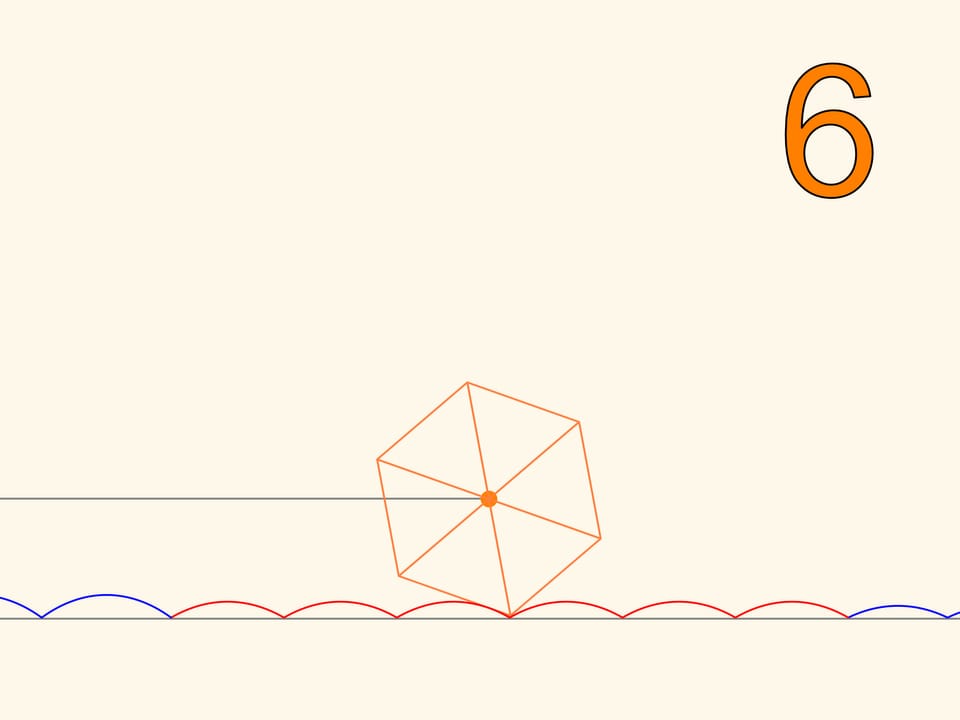
Observons la trajectoire du déplacement d’un des sommets du carré. Cette courbe ne coupe nulle part la chaînette, c’est-à-dire qu’on peut faire une voiture à roués carrées! Ainsi, la distance entre les axes de la voiture ne sont pas obligatoirement de longueur multiple a la bosse de la chaînette. Les roués peuvent être à différentes phases.
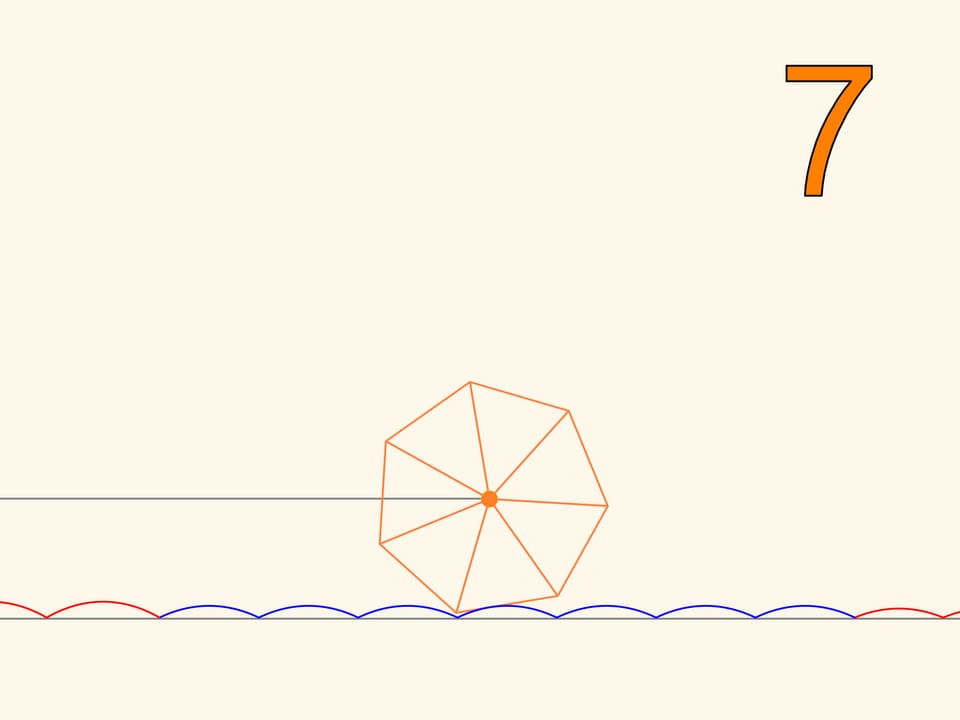
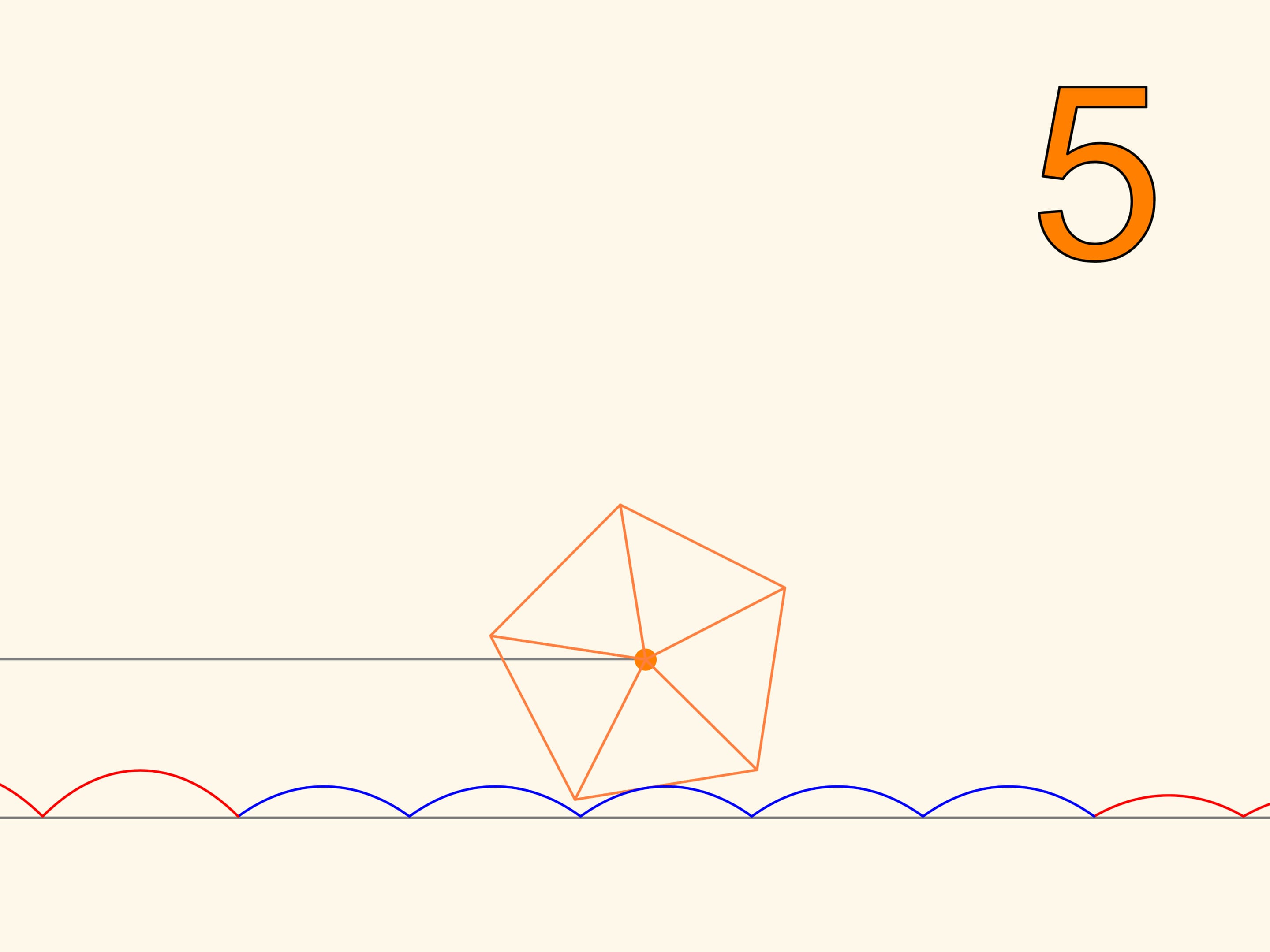
Nous avons appris à rouler avec des roués carrées. Il se trouve qu’on peut rouler avec des roués de différentes formes de polygones réguliers. La route doit seulement être non plane, ressemblant à une chaîne, avec connaissance du paramètre dépendant de la quantité d’angles. Selon le rapprochement du polygone régulier de la circonférence et d’un changement correspondant du paramètre, les arcs de la chaînette deviennent plus bas,la longueur horizontale du morceau, nécessaire pour tour du polygone, se rapproche de la longueur de la circonférence. Voilà comment est l’évolution des roues, qui, à la différence des polygones droits, se déplaçant sur une chaînette, savent tourner.
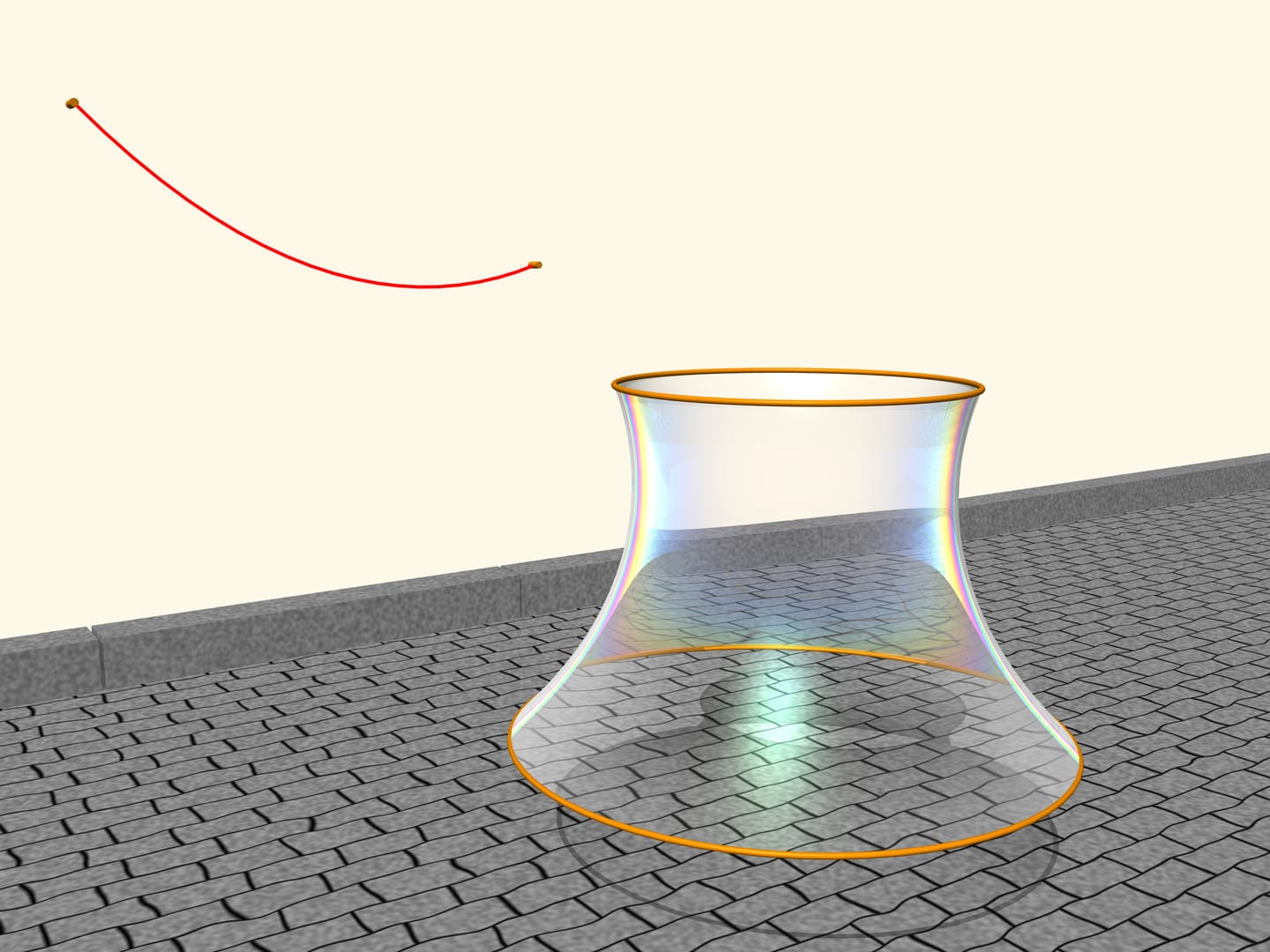
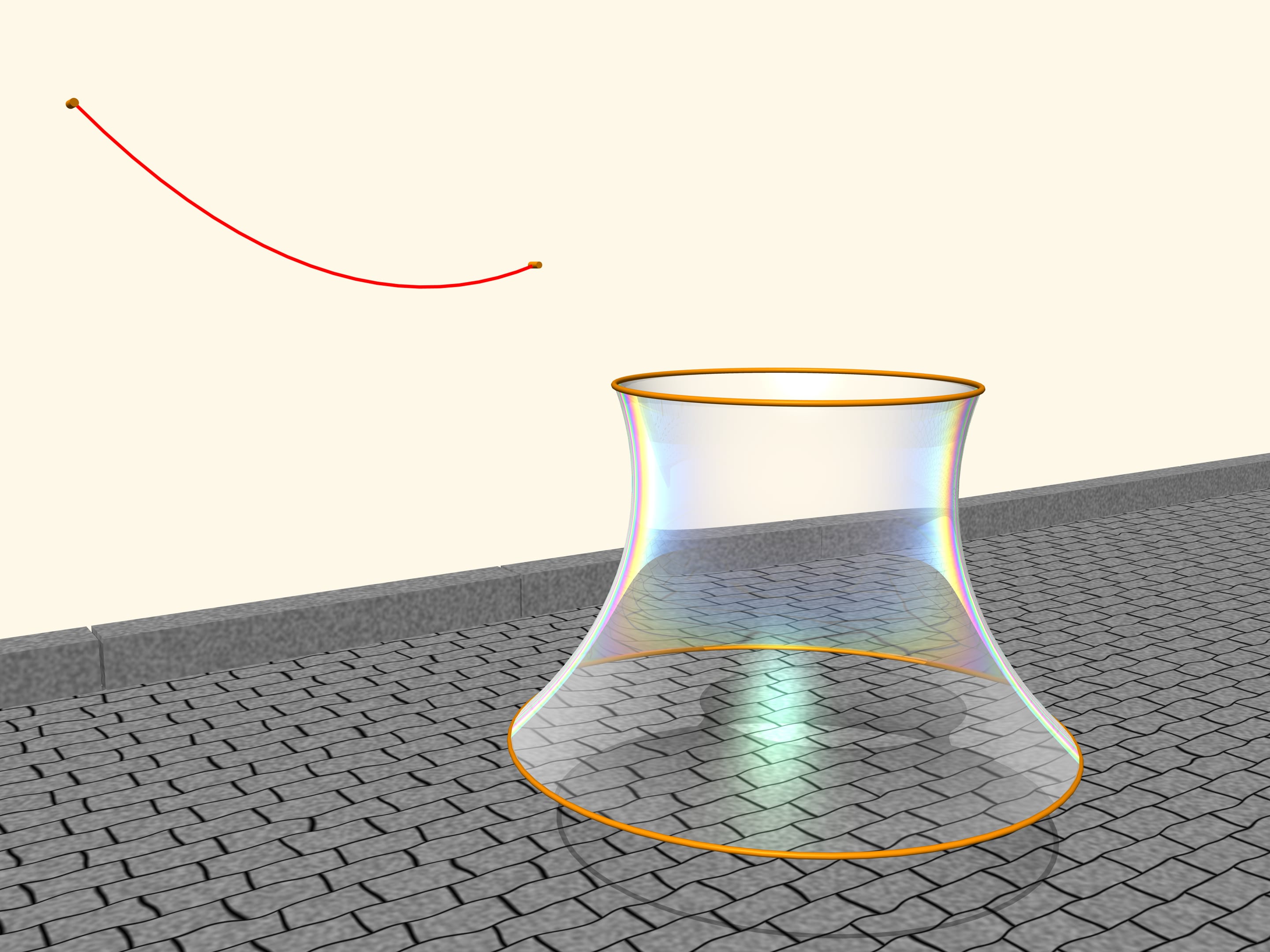
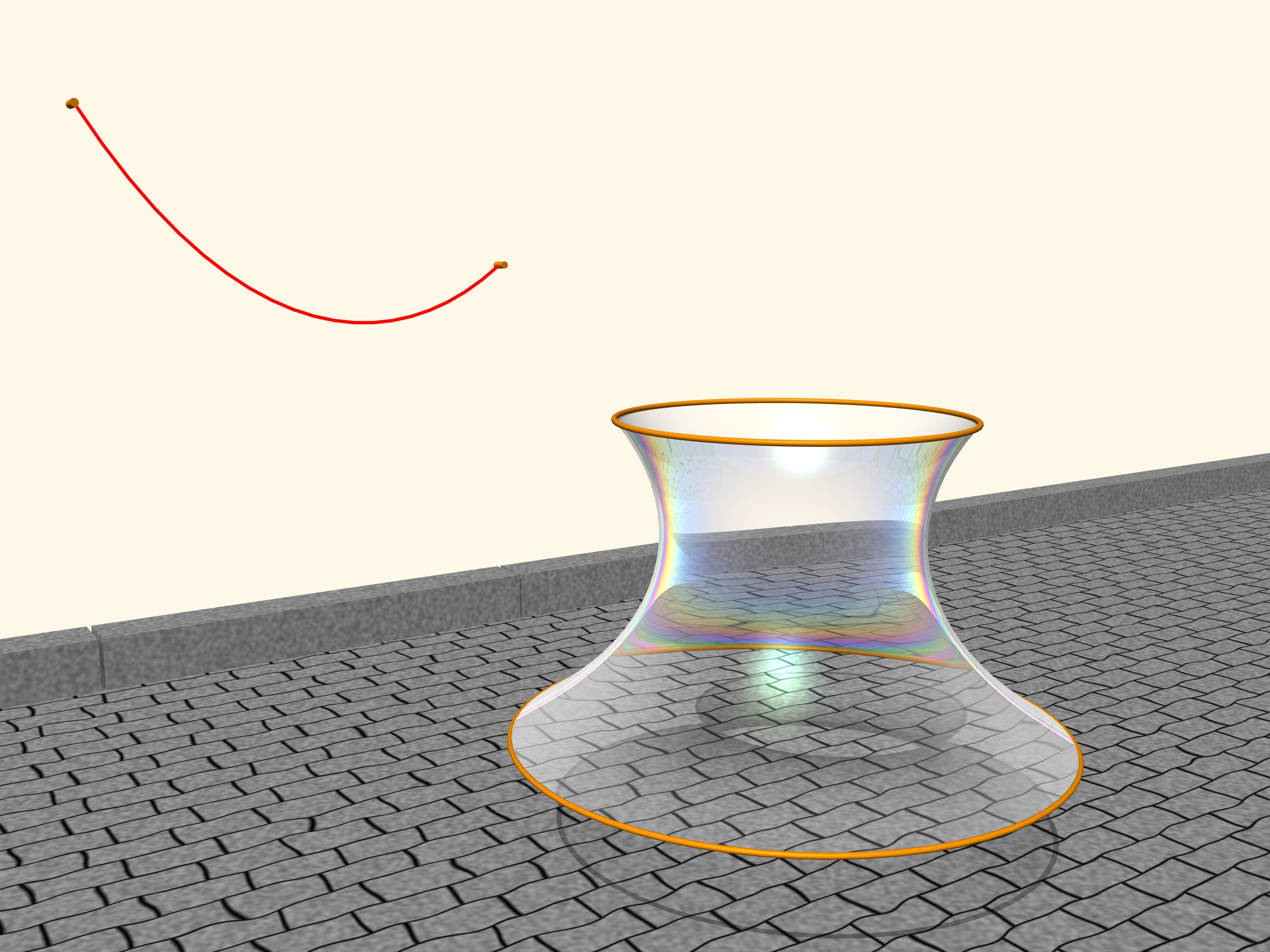
Tendons sur deux cercles, disposés sur deux plans parallèles, une .couche savonneuse. La couche savonneuse est un objet surprenant. Elle est légère, les forces intérieures sont beaucoup plus fortes que la force de pesanteur, à cause de ça, cette couche ressemble toujours à une surface ayant une aire infime selon les conditions de frontières données. Comment s’installe la couche de savon, étendue sur les cercles?
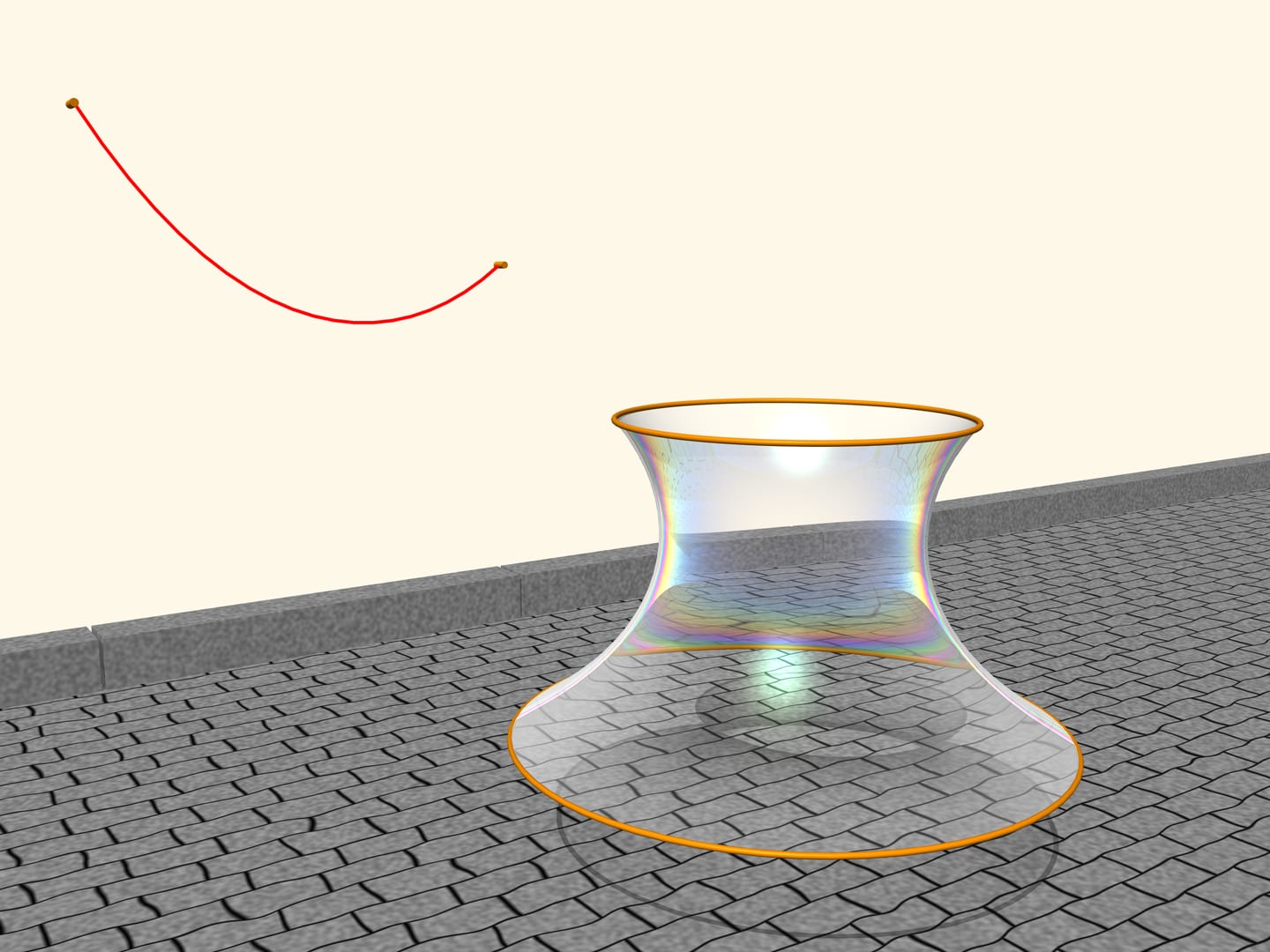
Il se trouve que ce sera la surface, caractérisée par la rotation de la chaîne. Si on change la distance entre les plans des cercles, la surface sera alors aussi changée, mais ressemblera toujours, de profil, à une chaîne de longueur donnée, suspendue conformément à sa disposition à des colonnes disposées. Léonard Euler a démontré cela en 1744, dans l’oeuvre “Méthode pour trouver des lignes courbes jouissant de propriétés de maximum ou de minimum, où la solution de problèmes isopérimétriques dans le sens le plus large”, il a nommé la surface caténoïde ( catena: chaîne en latin; idos: représentation, aspect en grec).