La cycloïde ⁠

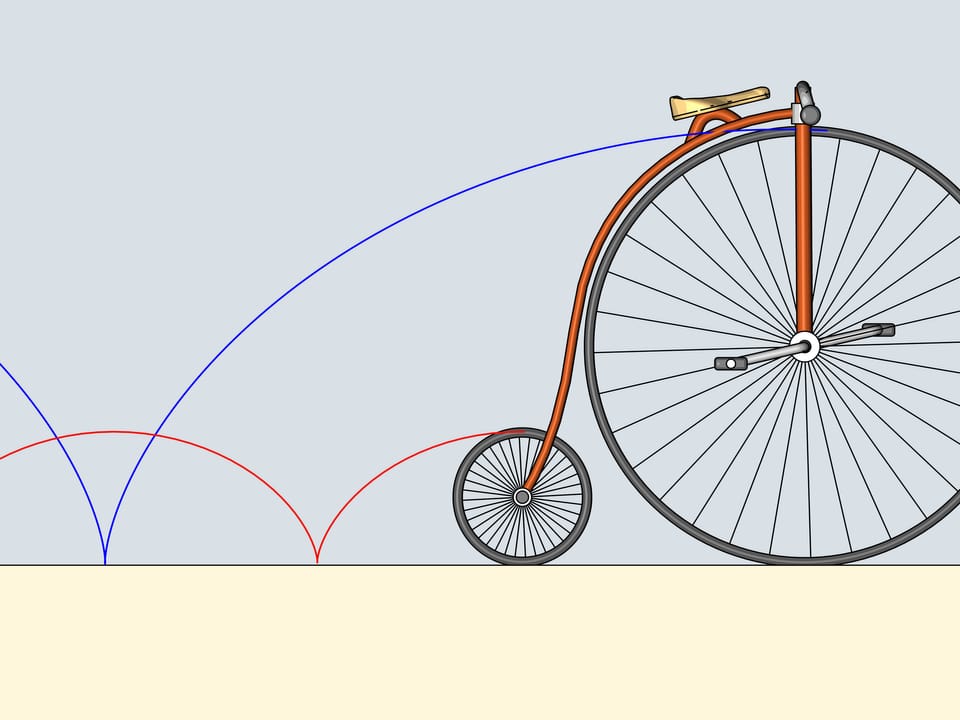
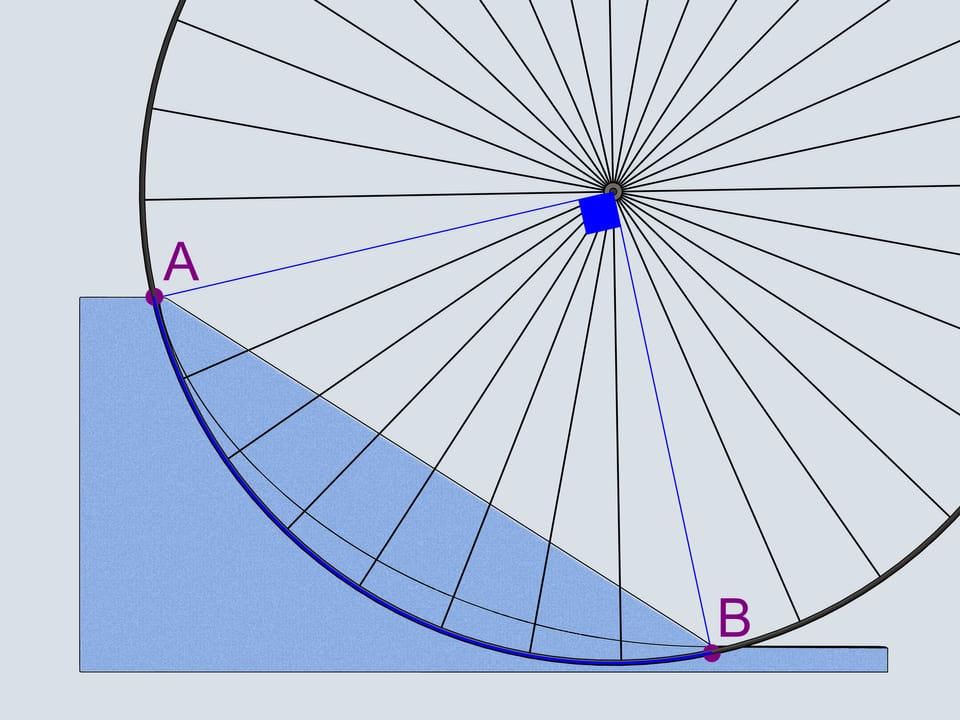
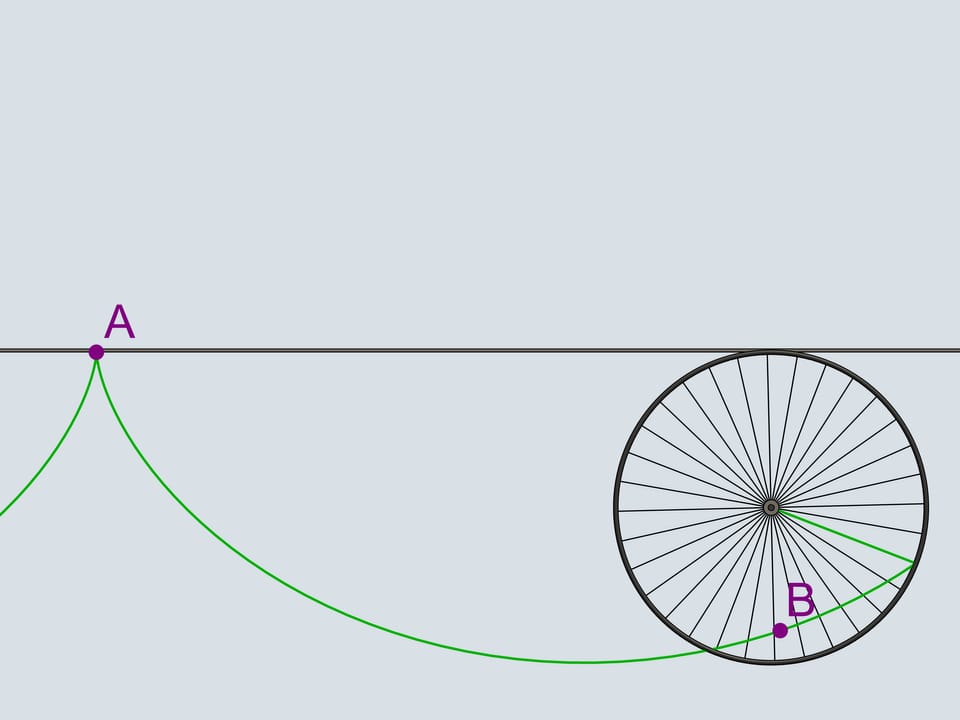
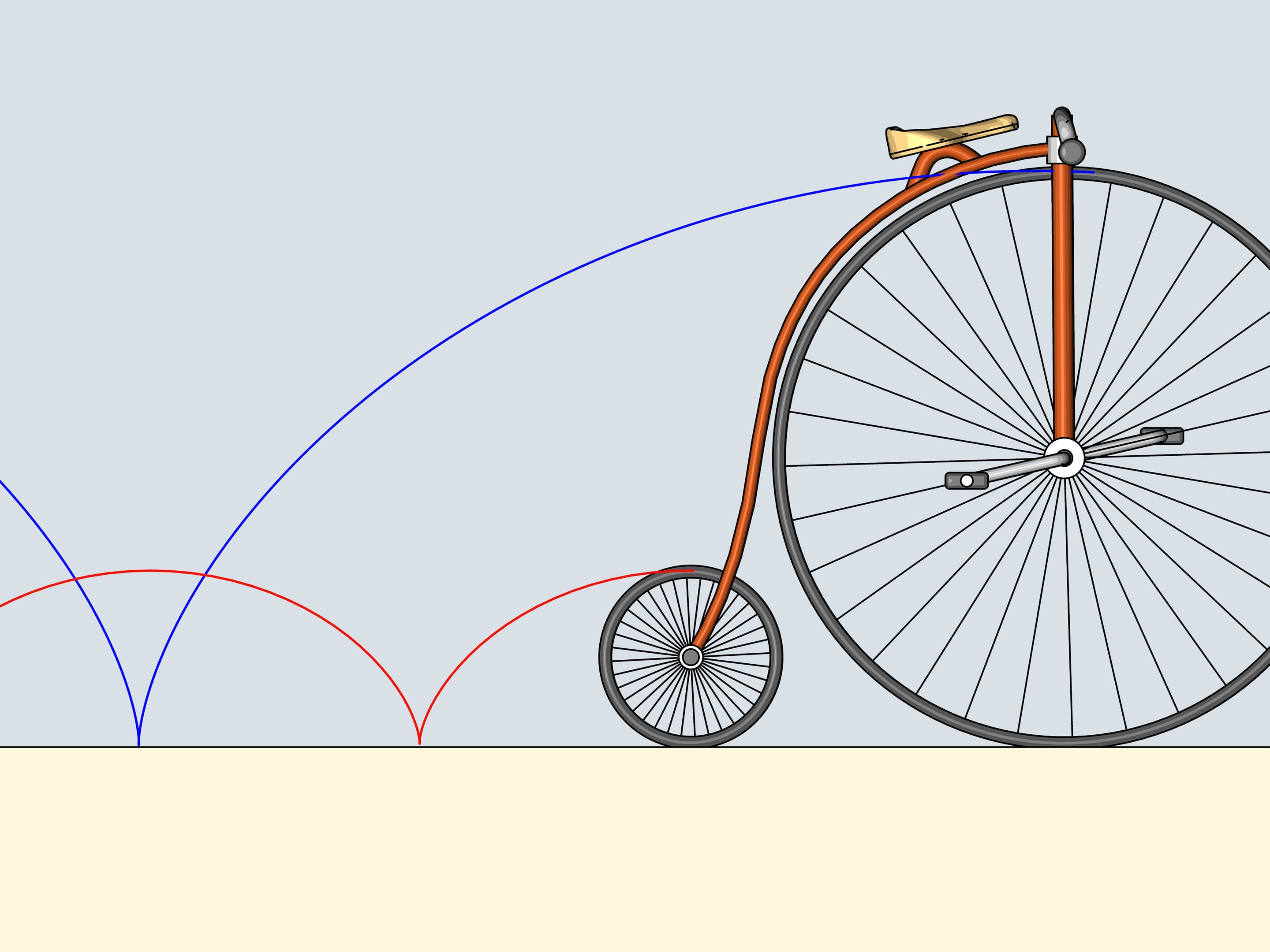
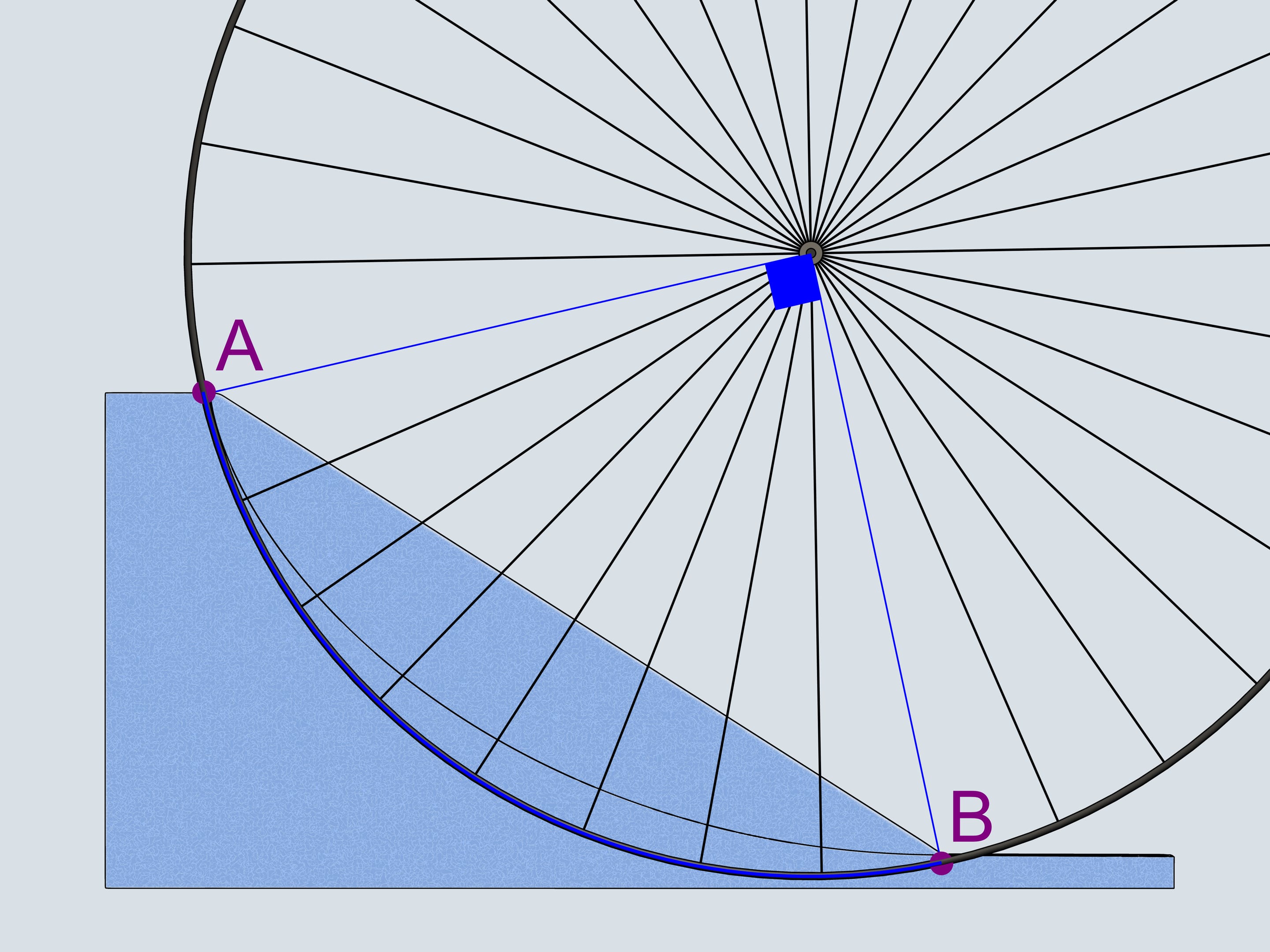
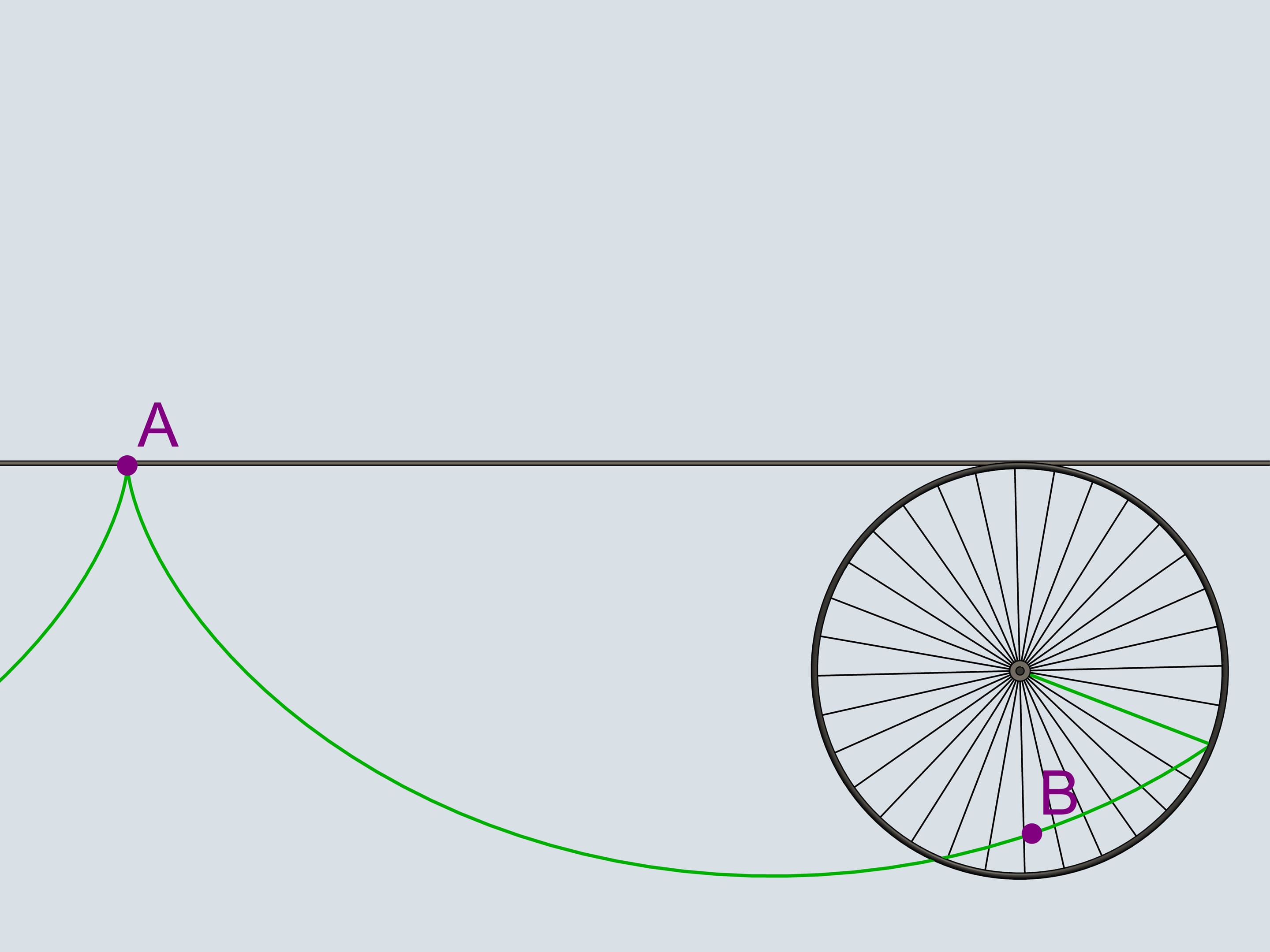
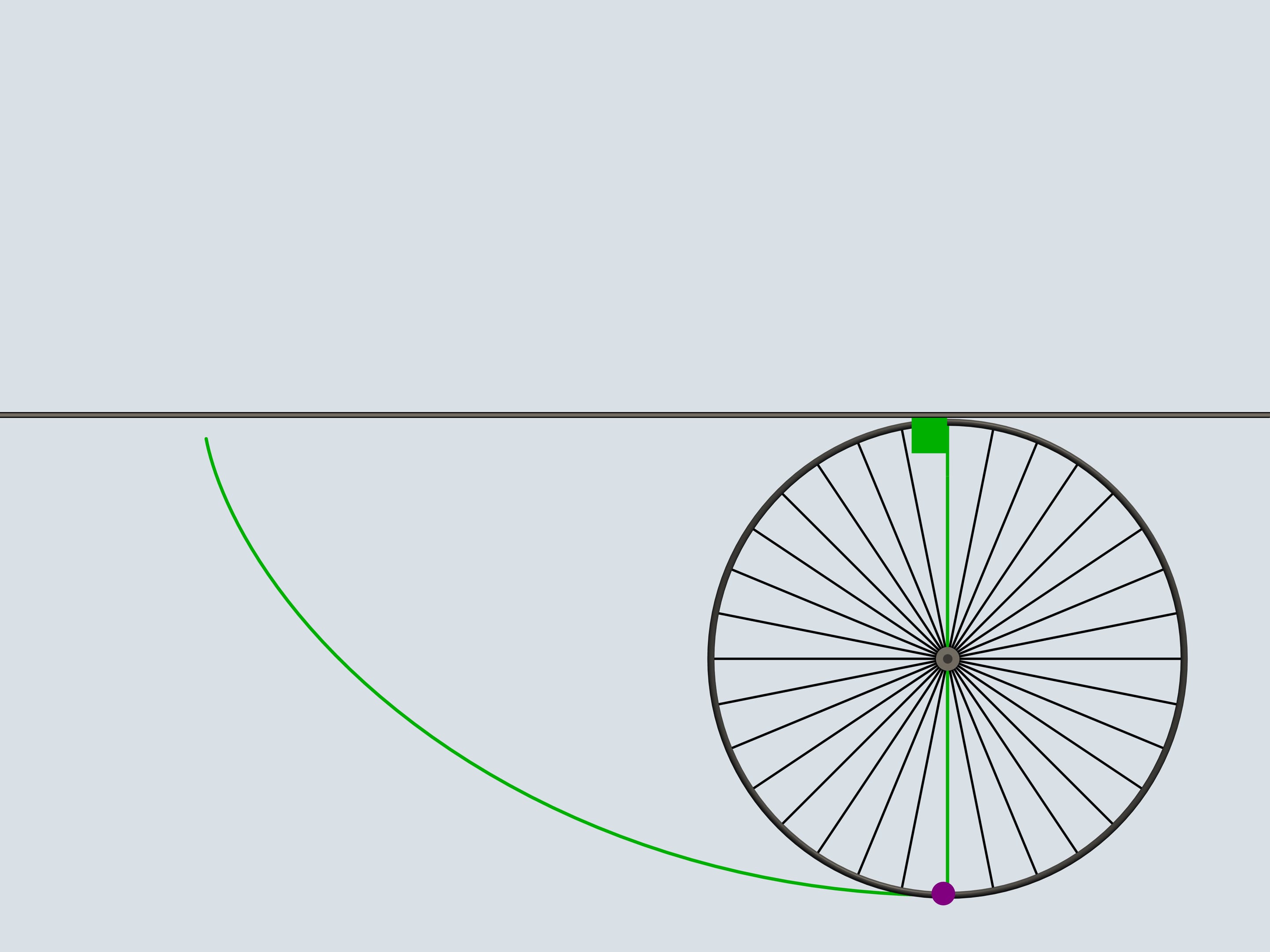
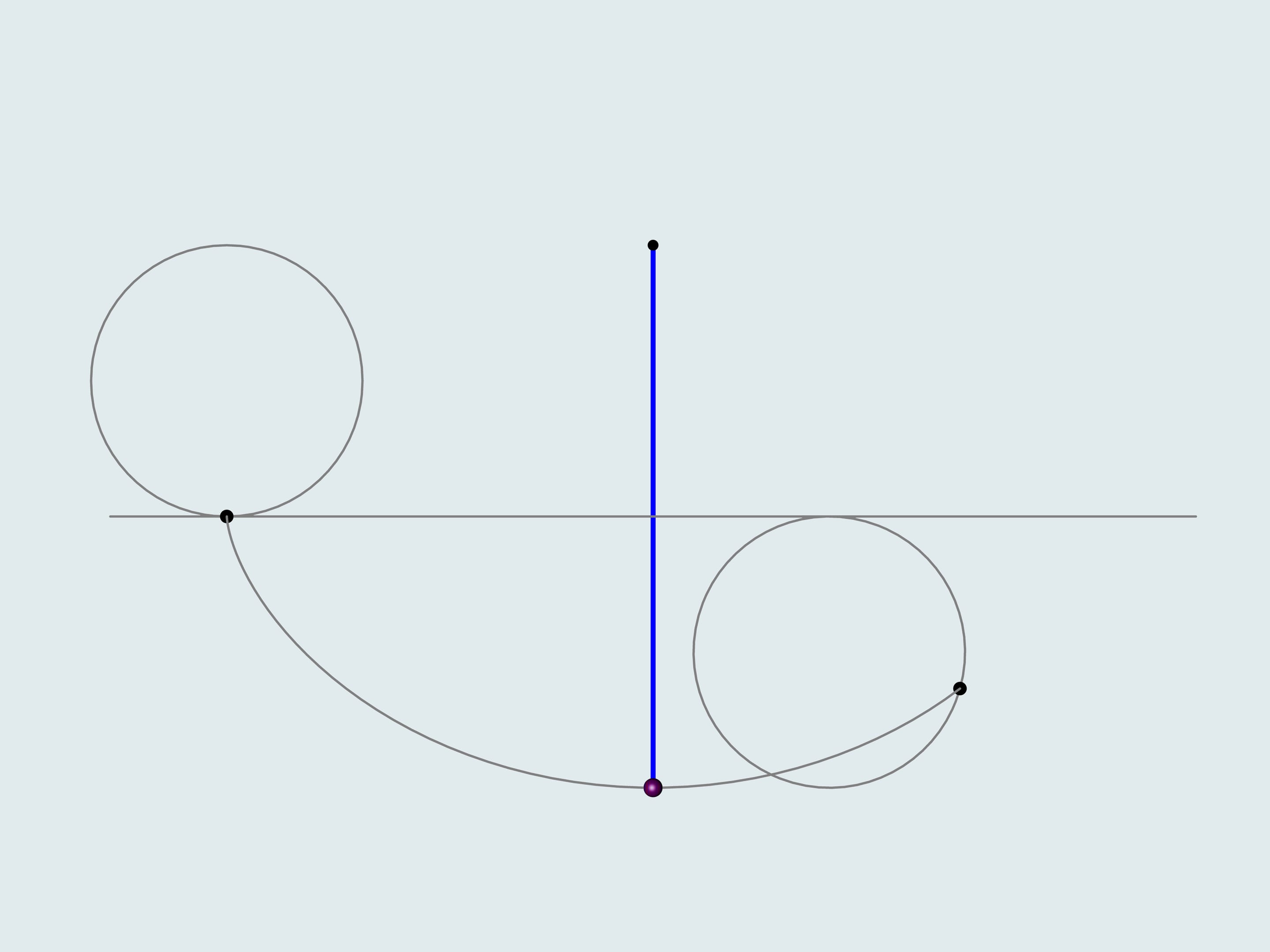
Vous souvenez vous de ces cata­photes en plas­tique orange, qu’on accro­chait aux rayons des roues du vélo? Nous accro­chons le cata­phote à la jante et en suivrons la trajec­toire. Les courbes ainsi obte­nues appar­tiennent à la famille des cycloïdes.

La roue est appelée dans ce cas «cercle géné­ra­teur de la cycloïde».

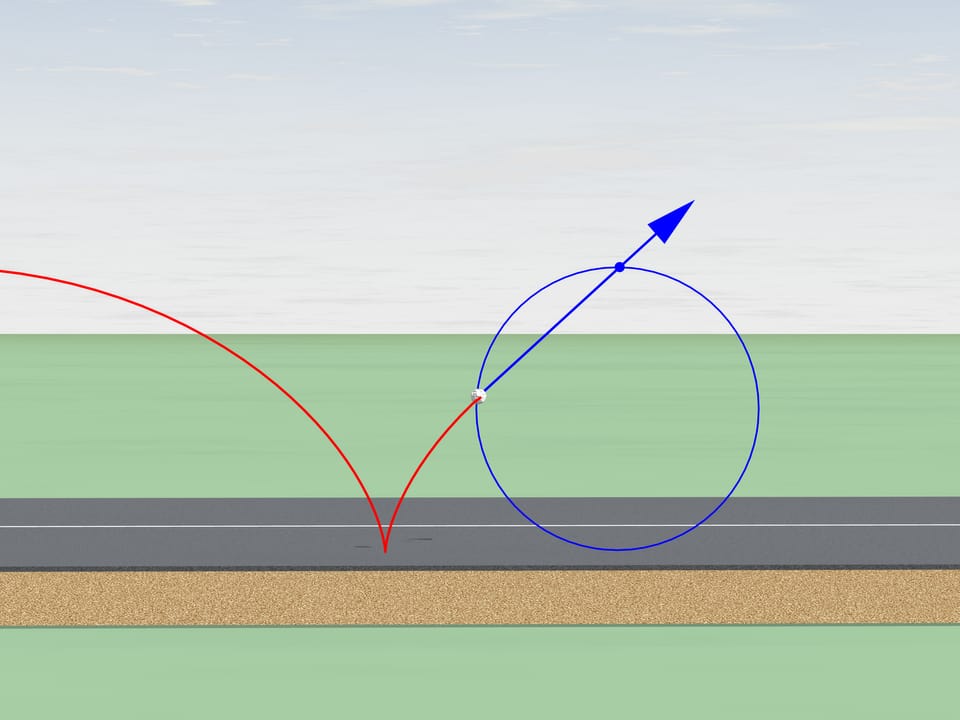
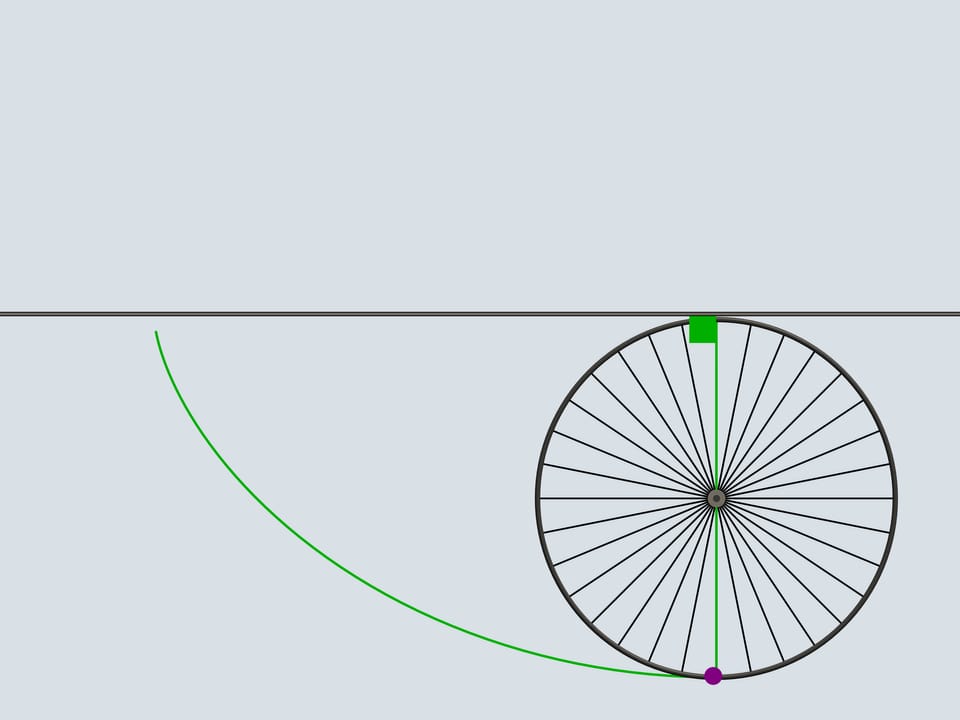
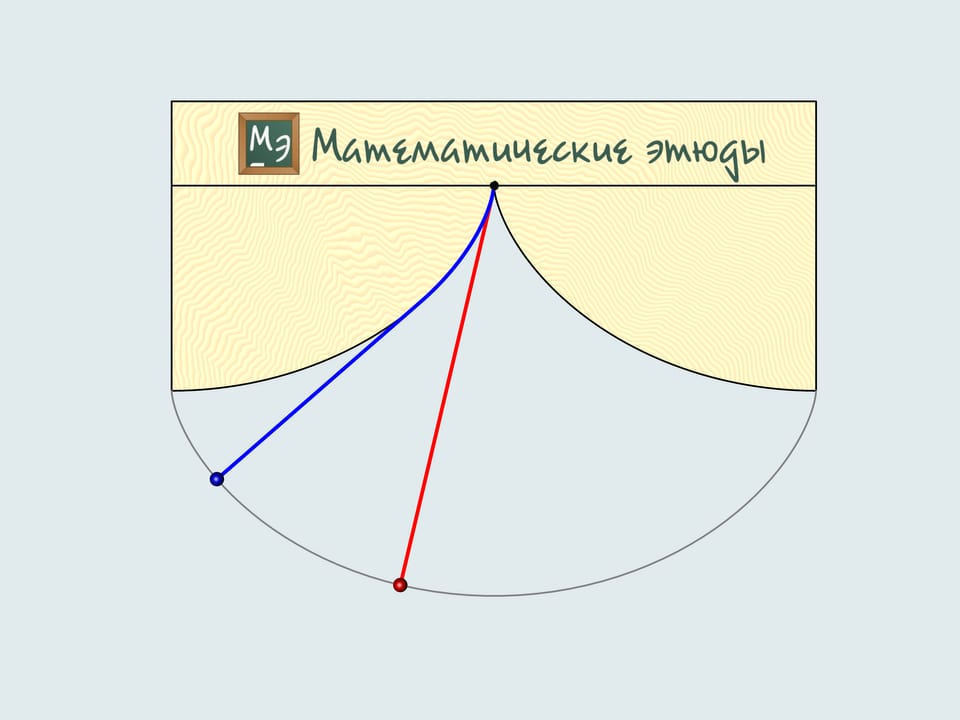
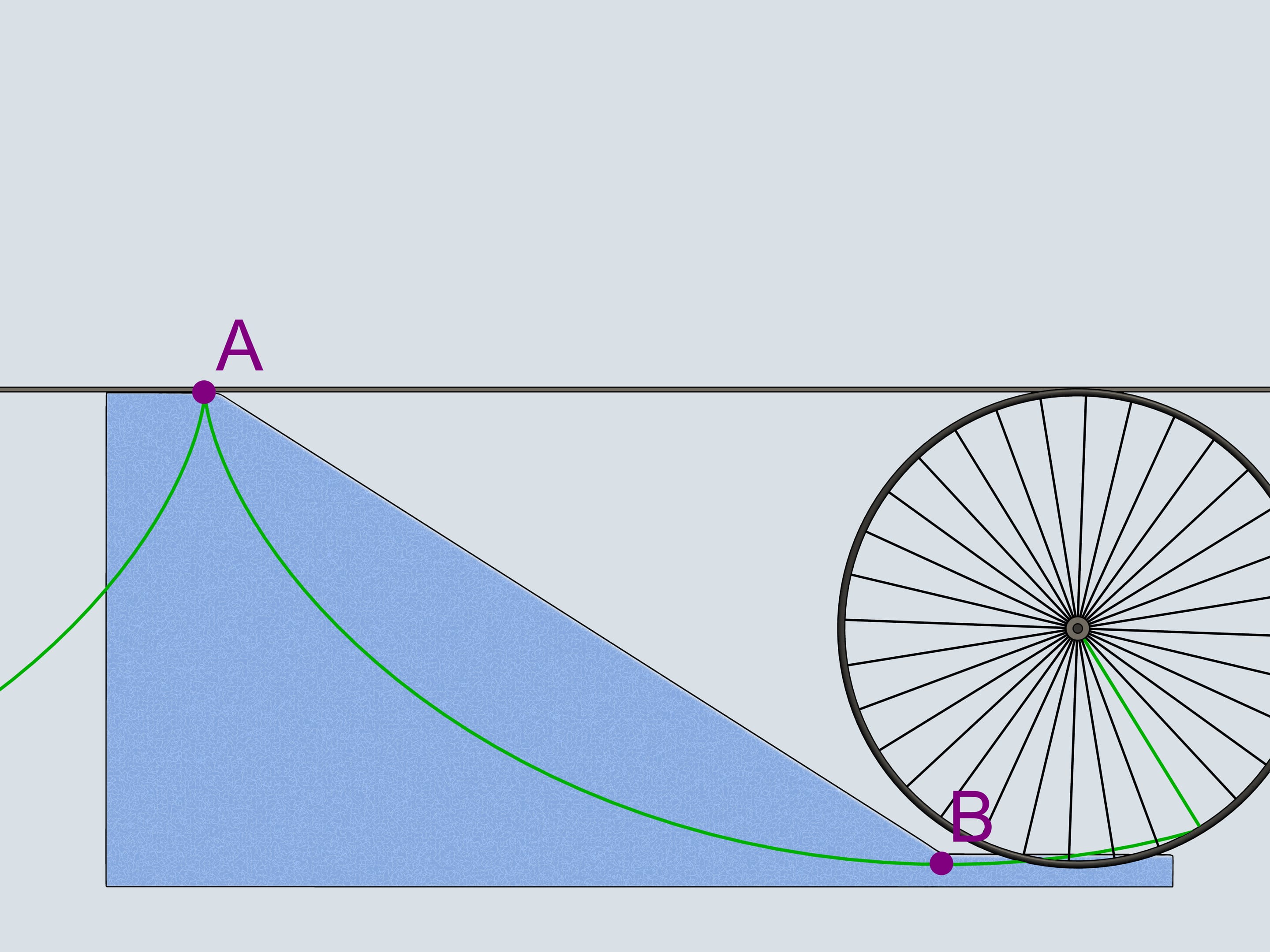
Mais reve­nons au siècle présent et déplaçons nous par un moyen plus modern. Sur le trajet d’une moto­cy­clette il y a un caillou qui s’est collé au pneu de la roue posté­rieure. Il tourne avec le roue un certain nombre de fois et enfin il se détache du pneu: dans quelle direc­tion volera–t–il? En direc­tion opposée à celle de la marche ou dans la même direc­tion?

Comme on le sait, le mouve­ment d’un corps libre commence en direc­tion de la tangente à la trajec­toire le long de laquelle il bougeait. La tangente à la cycloïde est toujours directe dans le sens de la marche et passe par le point plus haut du cercle géné­ra­teur. Notre caillou se dépla­cera donc dans la direc­tion de la moto­cy­clette.

Vous souvenez vous quand vous étiez des garçons et traver­siez les flaques d’eau sur un vélo sans les garde–boue arrière? Une bande mouillée sur votre dos était une confir­ma­tion de ce que nous venons d’obtenir.

Le XVIIe siècle a été le siècle de la cycloïde. Les plus grand scien­ti­fiques de cette époque étudièrent ses propriétés extra­or­di­naires.

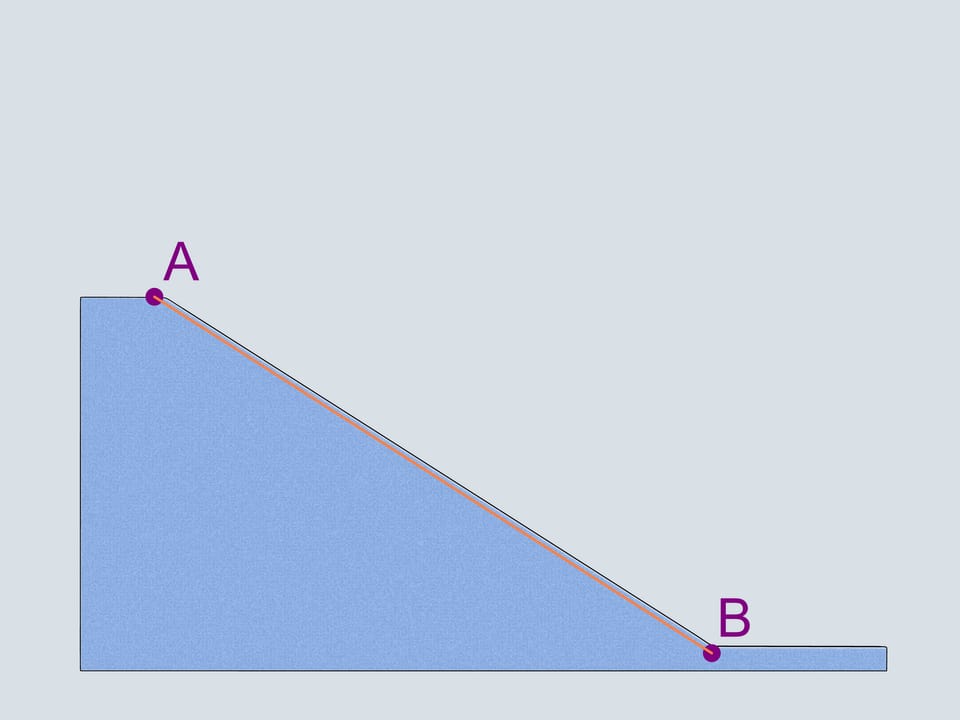
Quelle est la trajec­toire d’un corps qui, sous l’action de la gravi­ta­tion, bouge entre deux points donnés, dans le temps le plus bref? Cette ci a été une de premières ques­tions d’une disci­pline qui s’appelle main­te­nant calcul des varia­tions.

On peux mini­miser (ou maxi­miser) des choses diffé­rentes, la longueur d’un trajet, la vitesse, le temps. Dans le problème de la brachis­to­chrone on mini­mise exac­te­ment le temps (comme son nom l’indique: en grec brachistos signifie ’le plus bref’, chronos signifie temps).

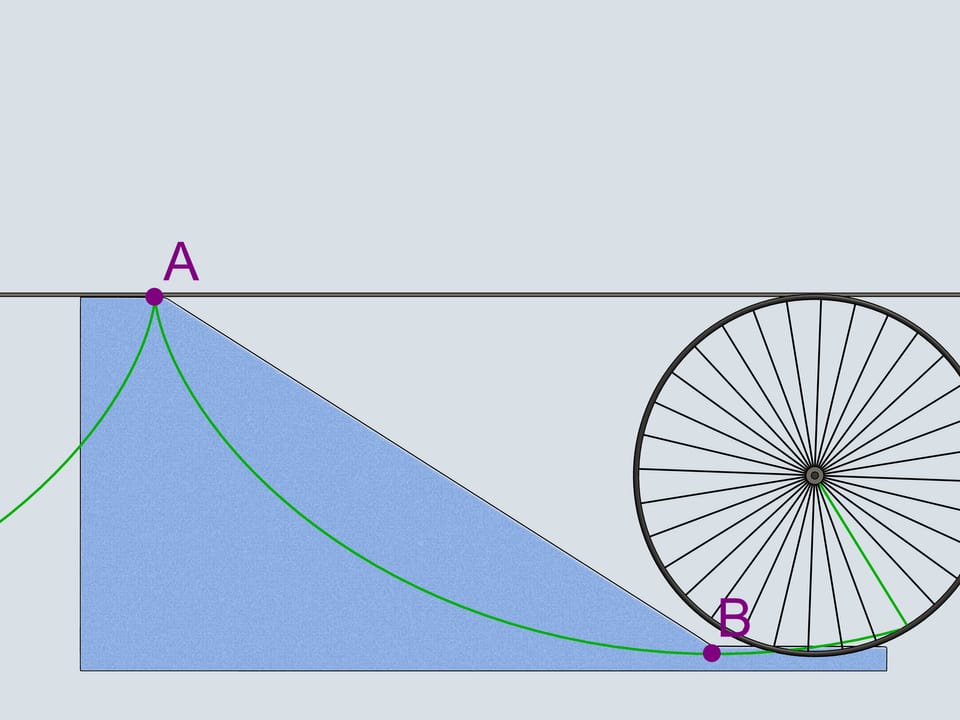
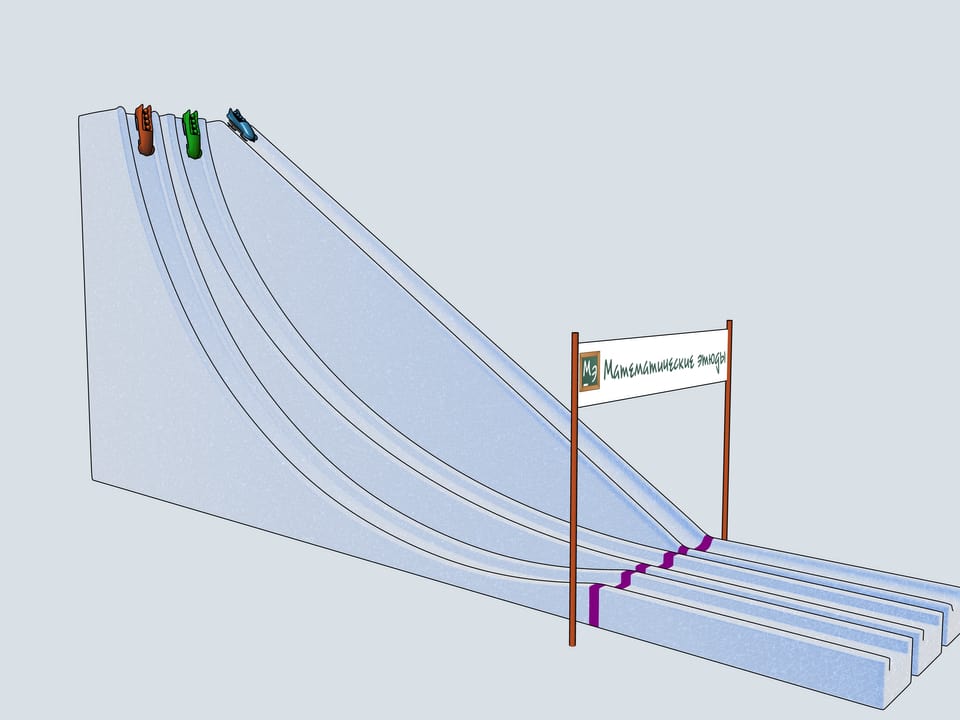
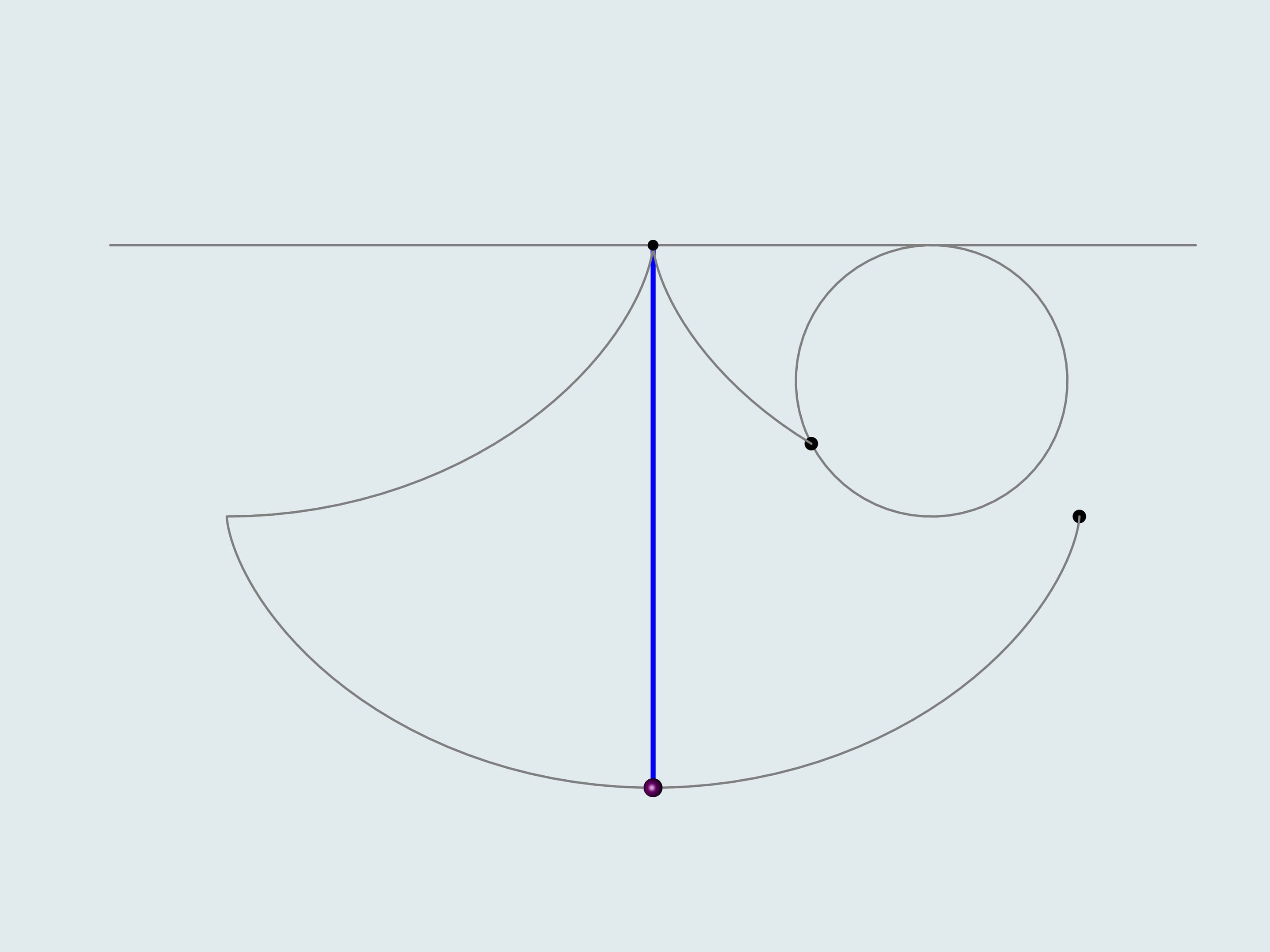
La première chose qui vient à l’esprit est une ligne droite. Mais nous consi­dé­rons égale­ment une cycloïde retournée avec le point de rebrous­se­ment qui coïn­cide avec le plus haut de deux points donnés. Enfin, selon Galilée, nous consi­dé­rons aussi un arc de cercle joignant les deux points, de 90 dégrées d’ouver­ture.

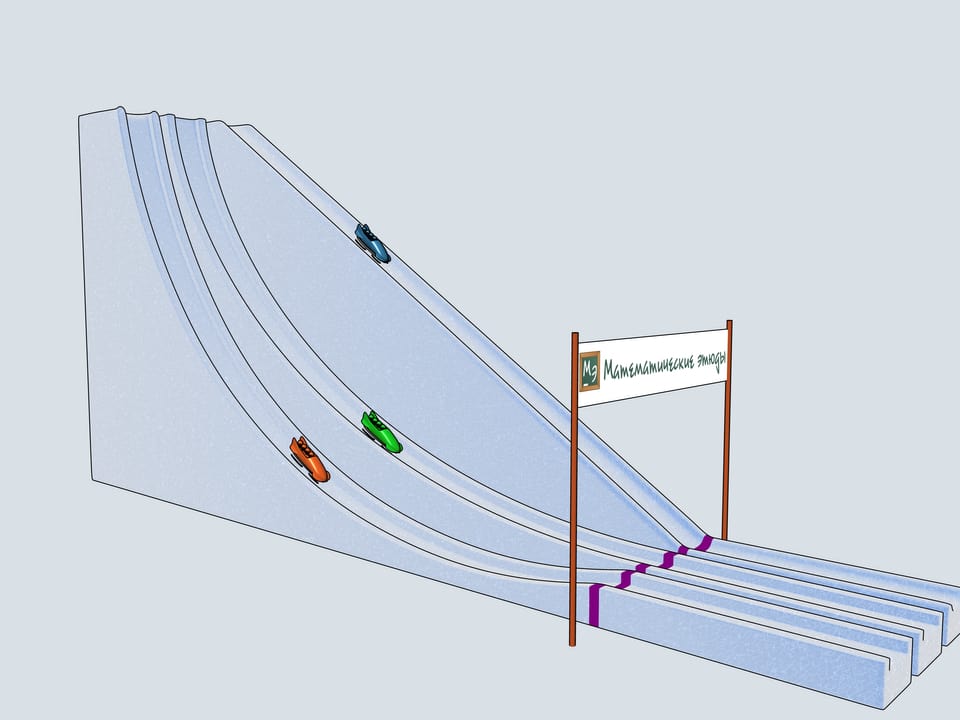
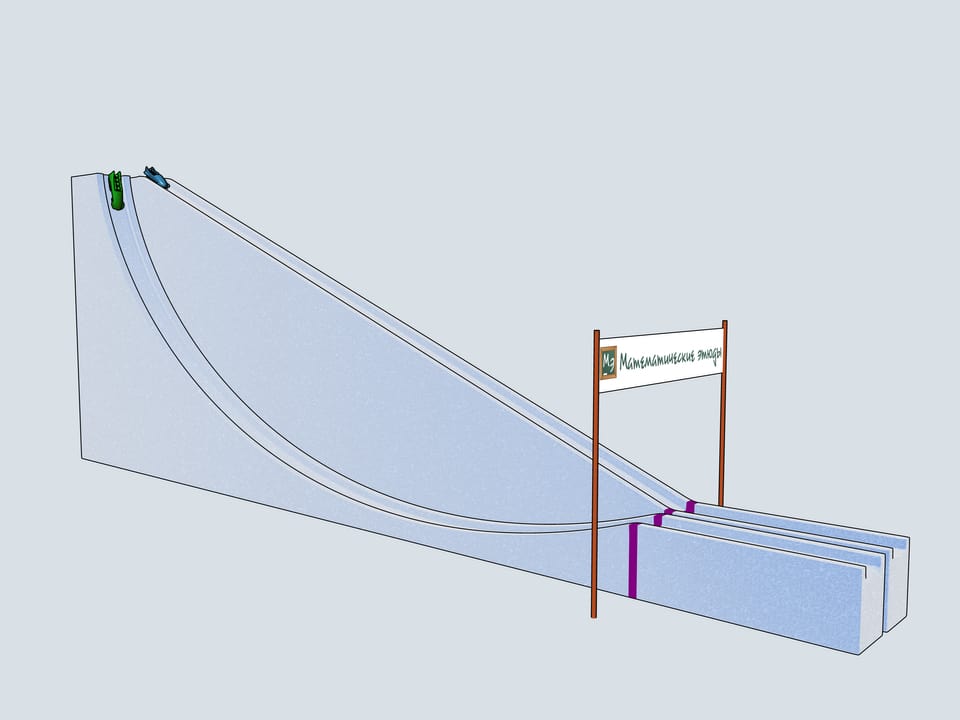
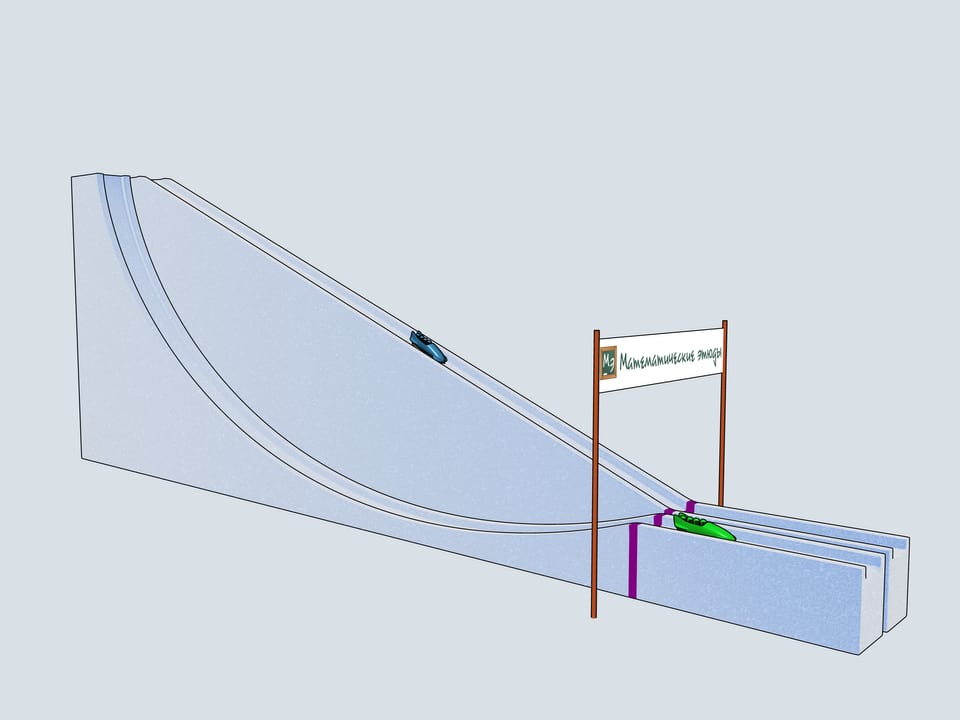
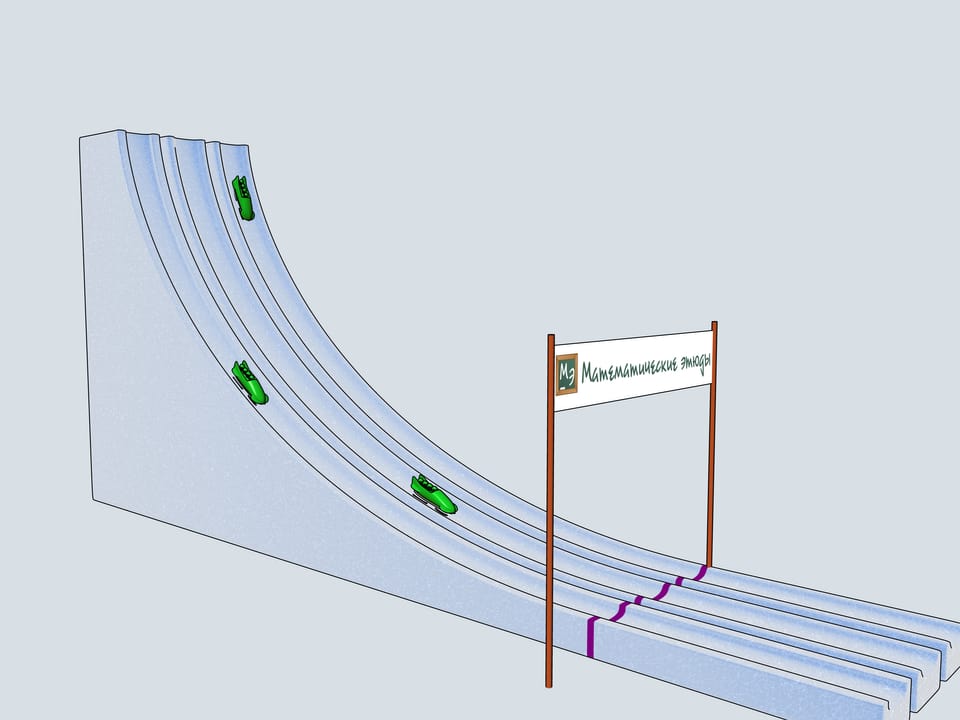
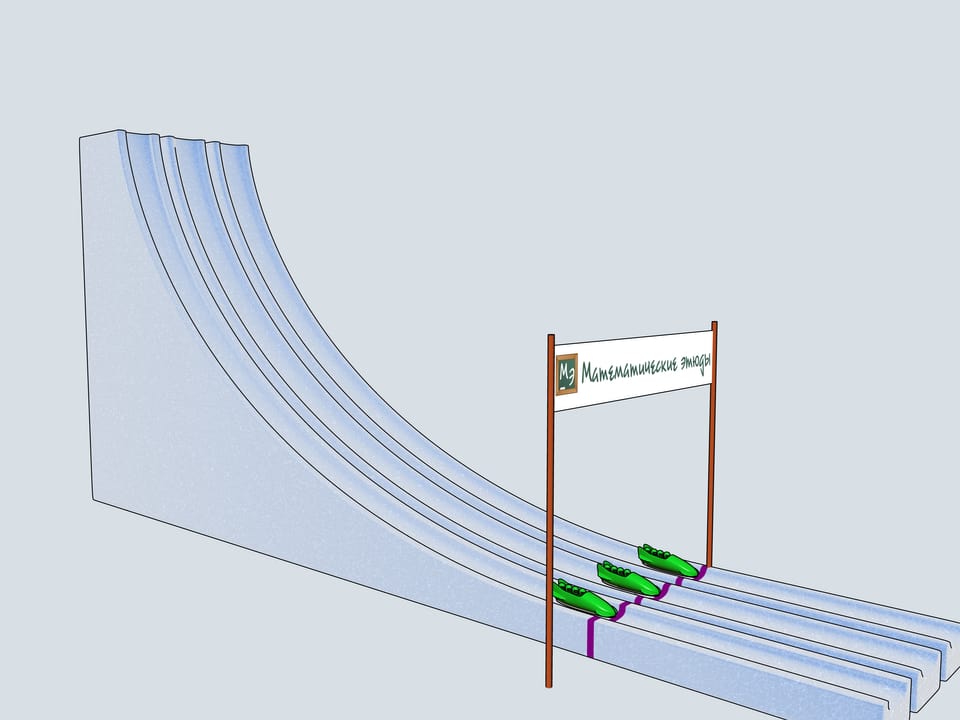
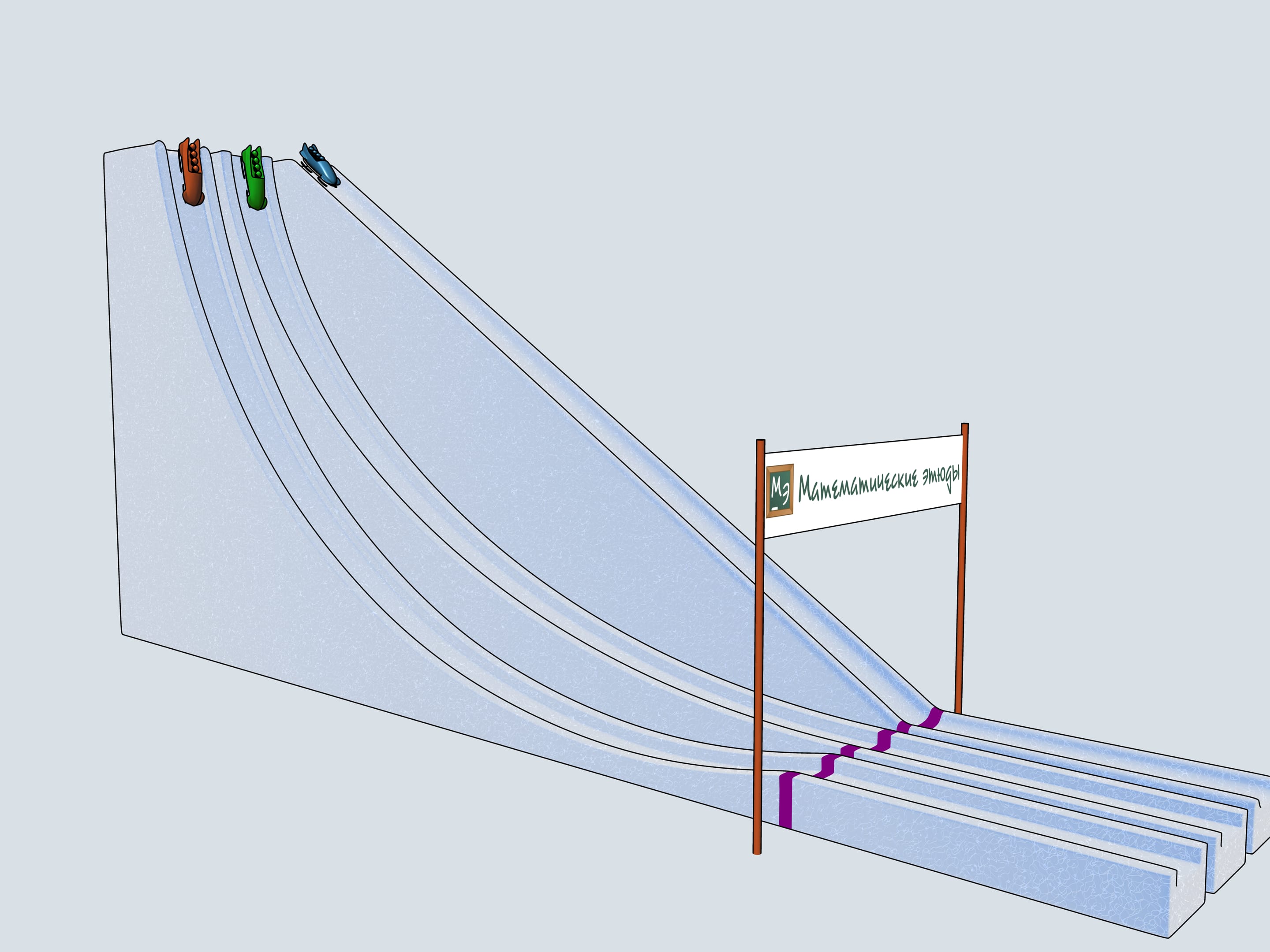
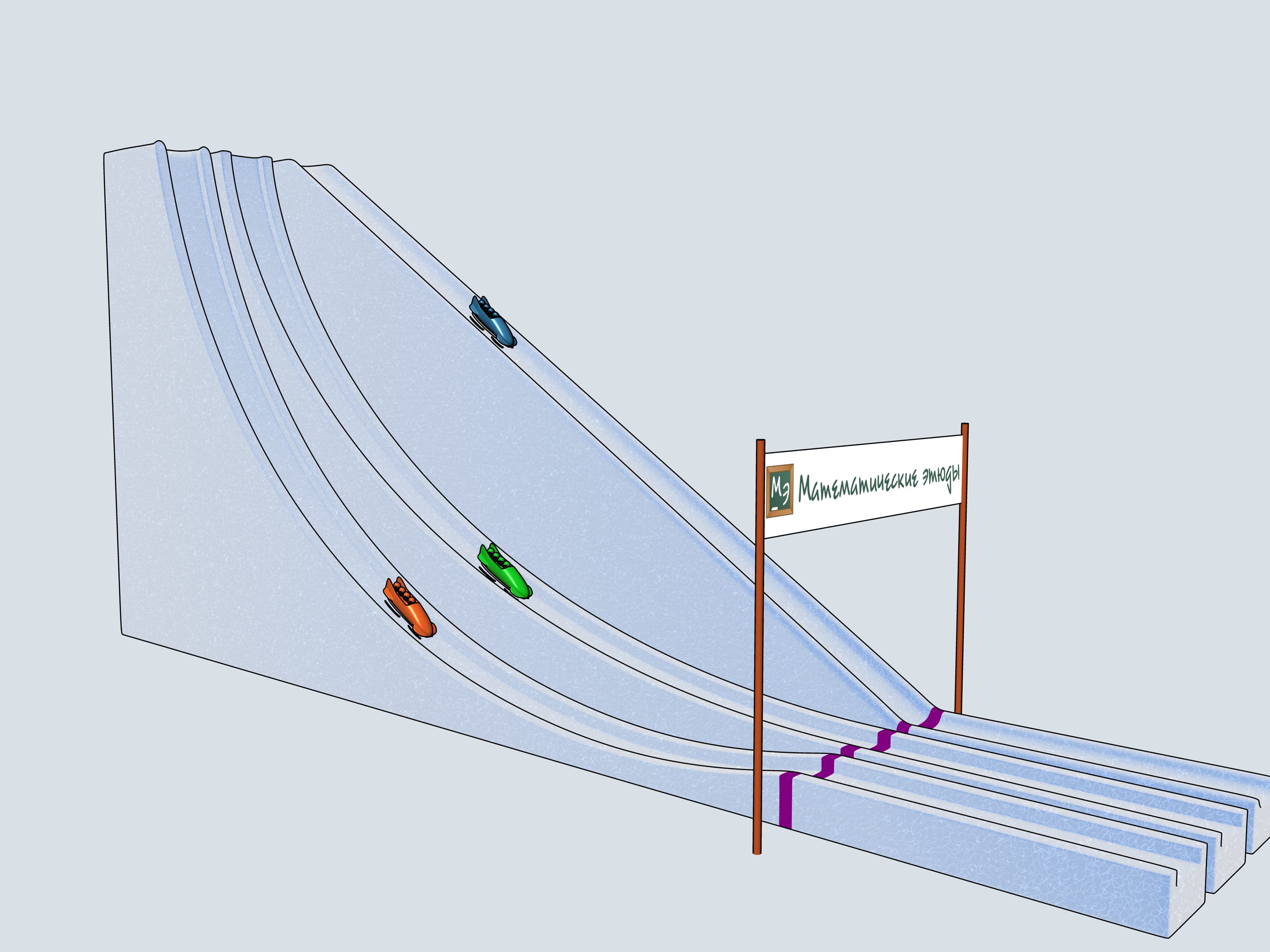
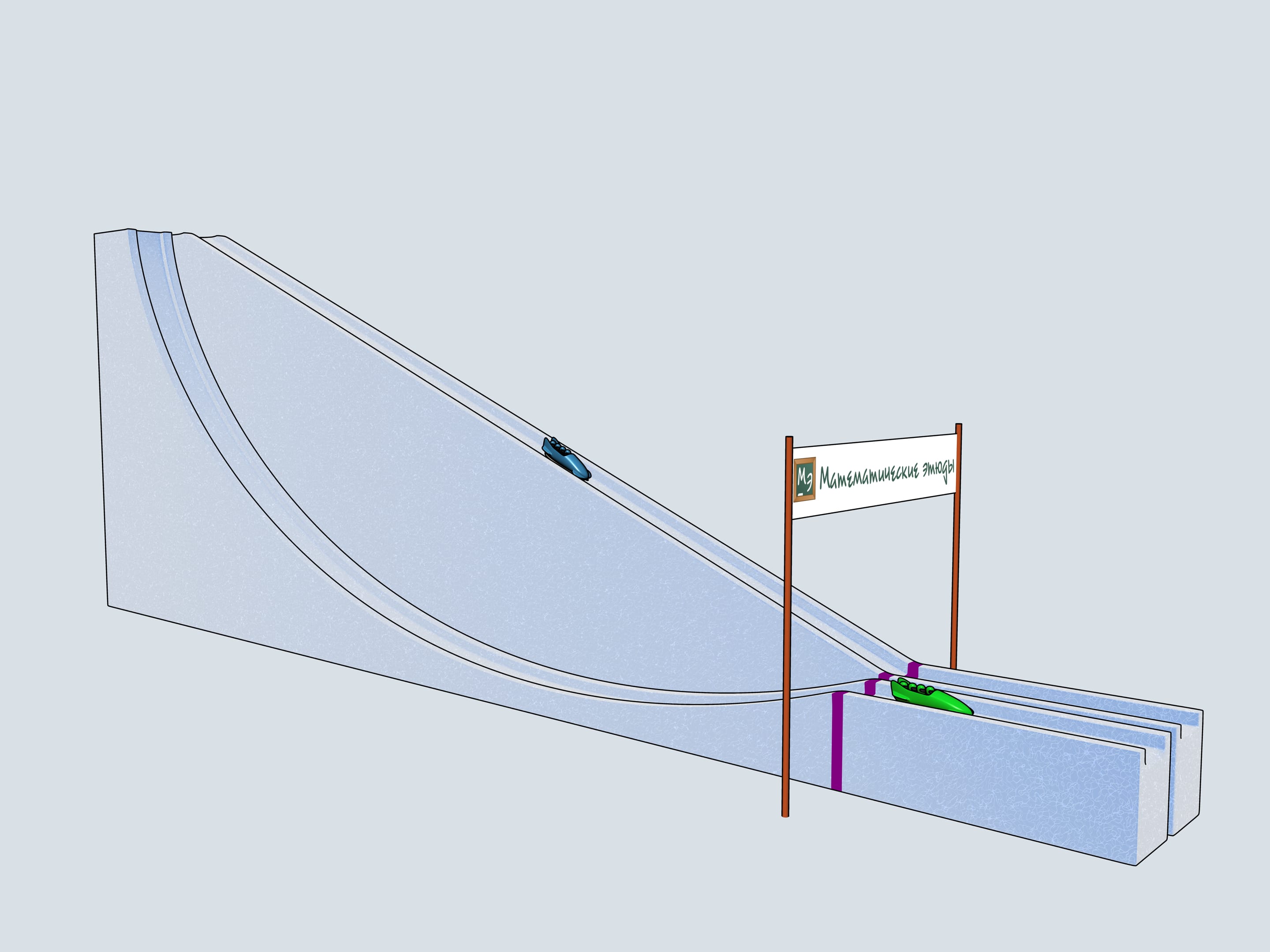
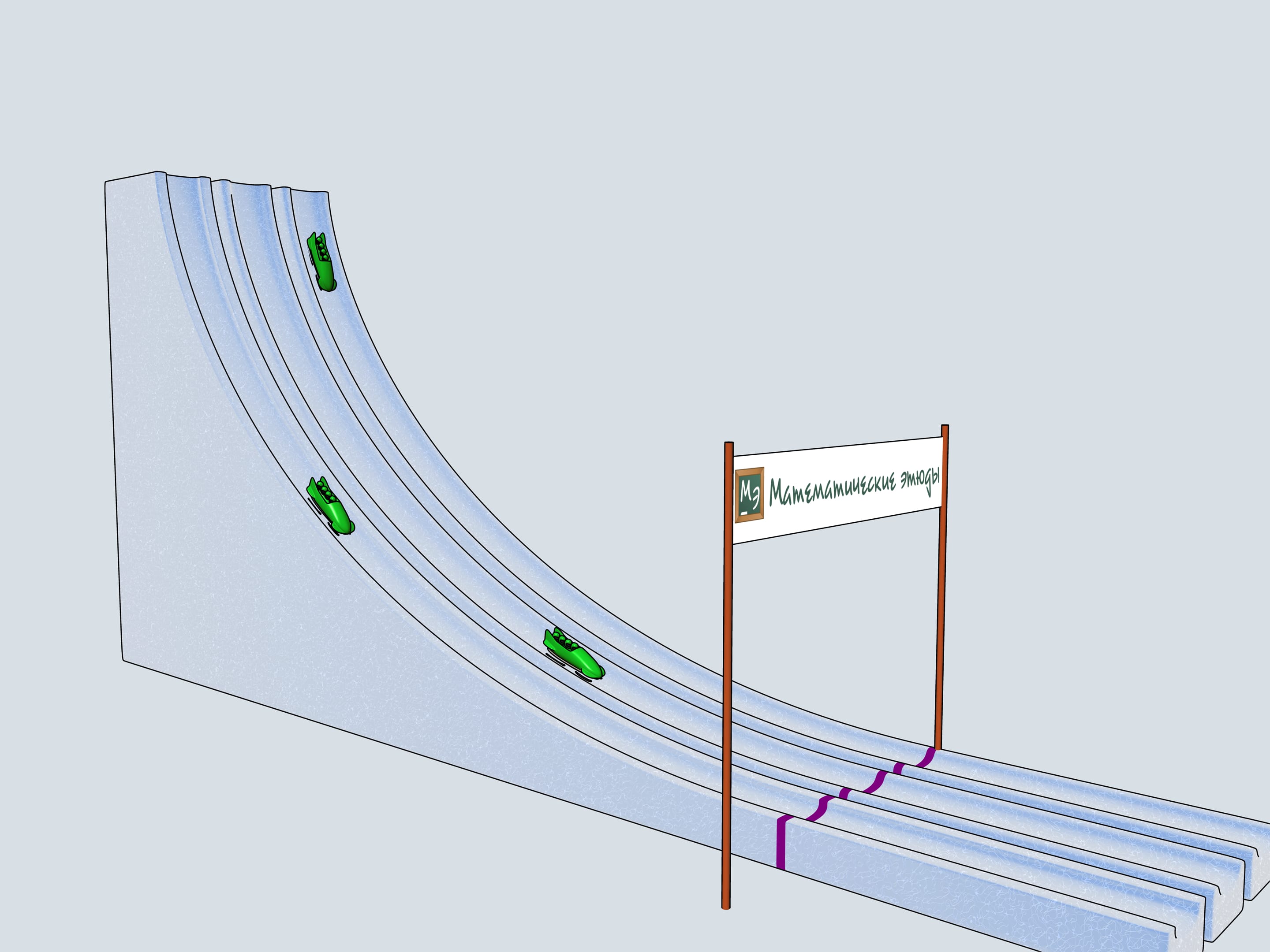
Nos allons construire trois pistes de bob ayant par profil les trois courbes consi­dé­rées et allons observer lequel des trai­neaux arrive en premier.

L’histoire du bob commence en Suisse. En 1924 les premiers jeux olym­piques d’hiver ont lieu à Chamonix en France, avec équipes de deux et de quatre personnes. Seule­ment en 1928 l’équipe était composée de cinq hommes. Depuis cette année le bob a été toujours de deux ou de quatre. Parmi les règles du bob il y a des choses inté­res­santes. Natu­rel­le­ment, il existe une limite de poids soit pour le trai­neau soit pout l’équipe, mais il existe aussi des restric­tions sur les maté­riaux à utiliser pour les patins (la paire de patins à l’avant est mobile et est relié au gouver­nail, la paire arrière est fixe).

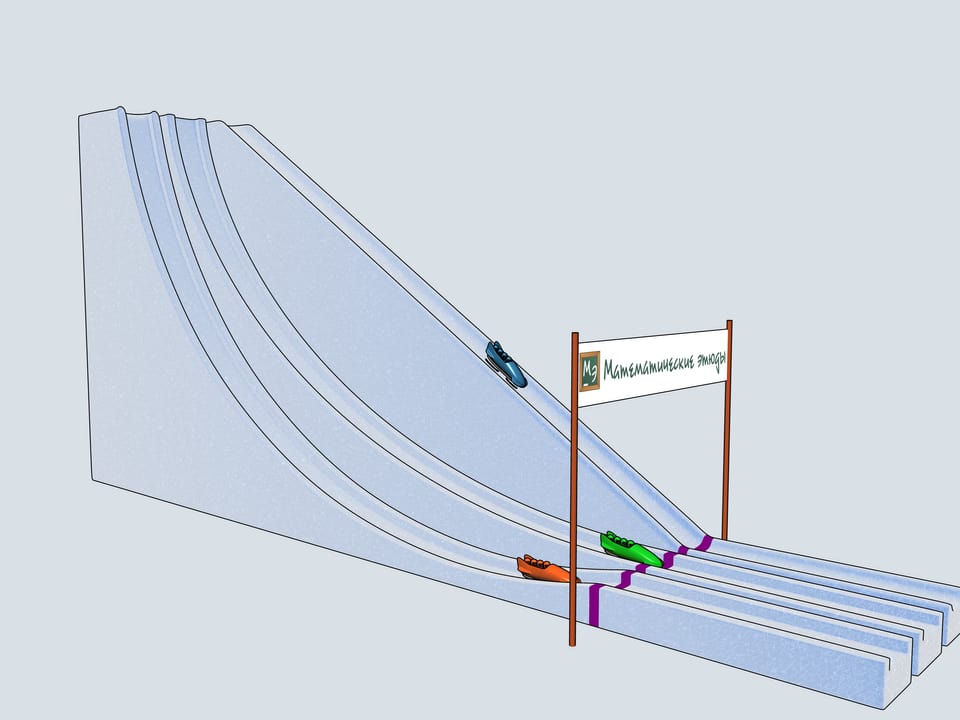
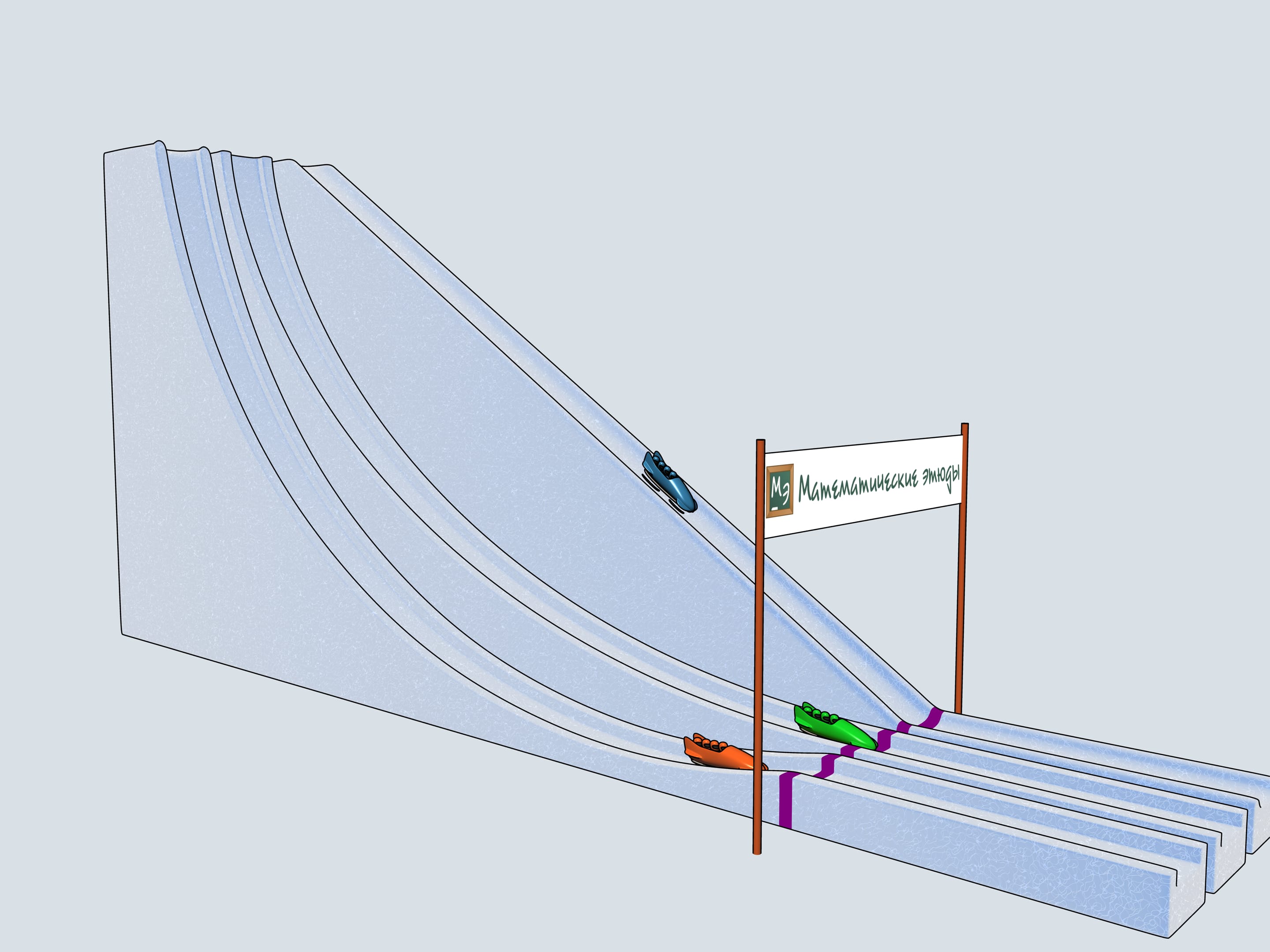
Donnons le départ à nos bobs à quatre. Lequel des trois arri­vera à la ligne d’arrivée en premier? Le bob vert, commandé par les Etudes Mathé­ma­tiques, suivant la piste de la cycloïde, est arrivé en premier!

Mais pourquoi Galilée avait examiné le quart de cercle, croyant qu’il aurait réduit le temps de la descente? Il avait inscrit dans l’arc de cercle une ligne poly­go­nale, brisé, et avait observé que le temps de descente s’accour­cis­sait comme le nombre d’éléments de la poly­go­nale augmen­tait. De cette façon Galilée est arrivé à l’arc de cercle, mais à tort il a tiré la conclu­sion que cette trajec­toire est la meilleure de toutes les trajec­toires possibles. Comme nous l’avons vu, la cycloïde est meilleure. Et, par le calcul des varia­tions, on démontre que la cycloïde est la meilleur parmi toutes les courbes possibles.

Entre deux points donnés on peut tracer une seule cycloïde, à la condi­tion que le point le plus élevé coïn­cide avec le point de rebrous­se­ment. Même lorsque la cycloïde a un morceau de montée, pour atteindre le second point, la cycloïde sera toujours la courbe entre les deux points qui est parcourue dans le temps le plus bref!

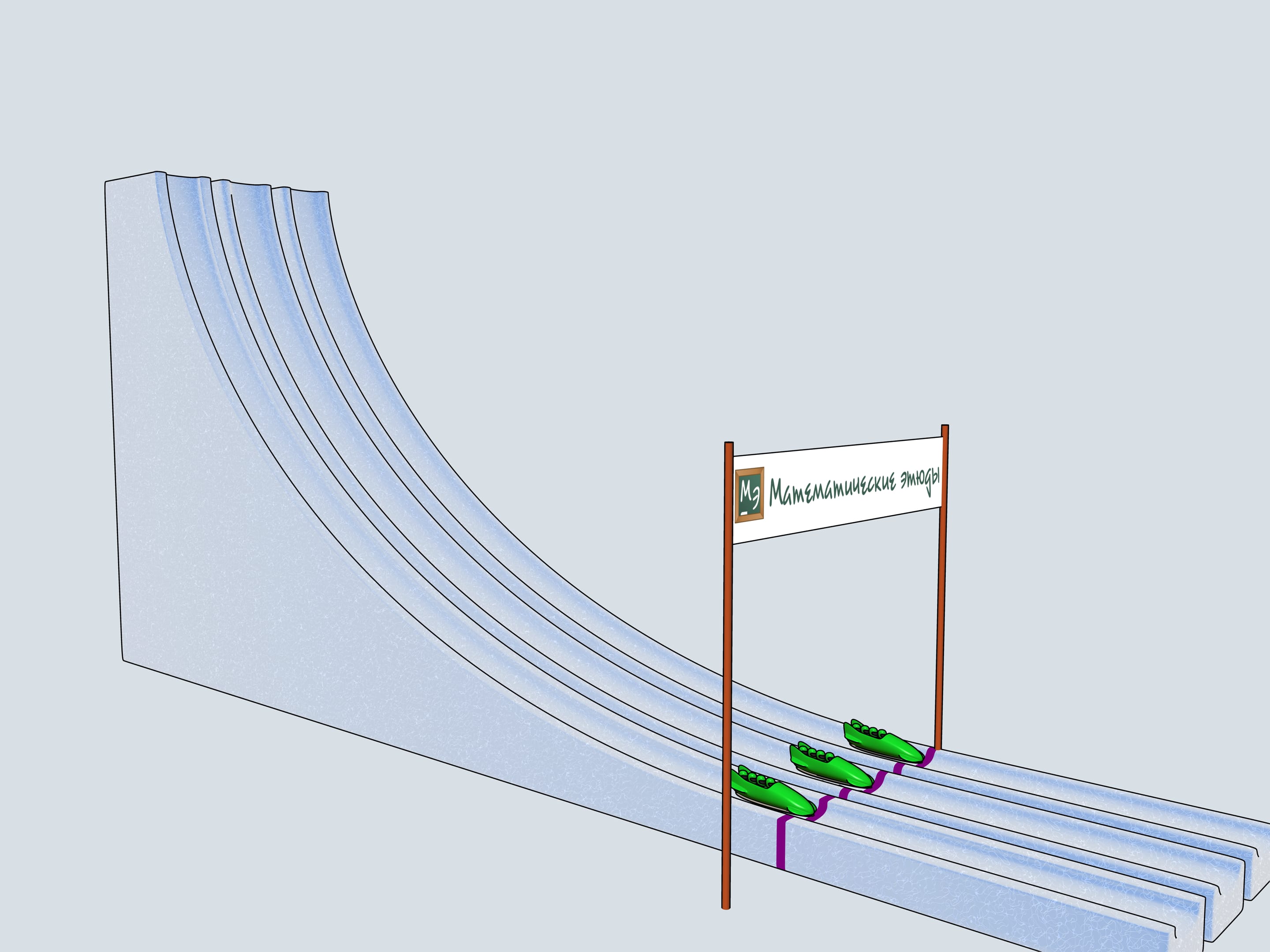
La cycloïde possède encore une propriété inté­res­sante, qui concerne le problème de la tauto­chrone. Toujours en grec, tautos signifie même, et chronos, comme nous le savons, temps.

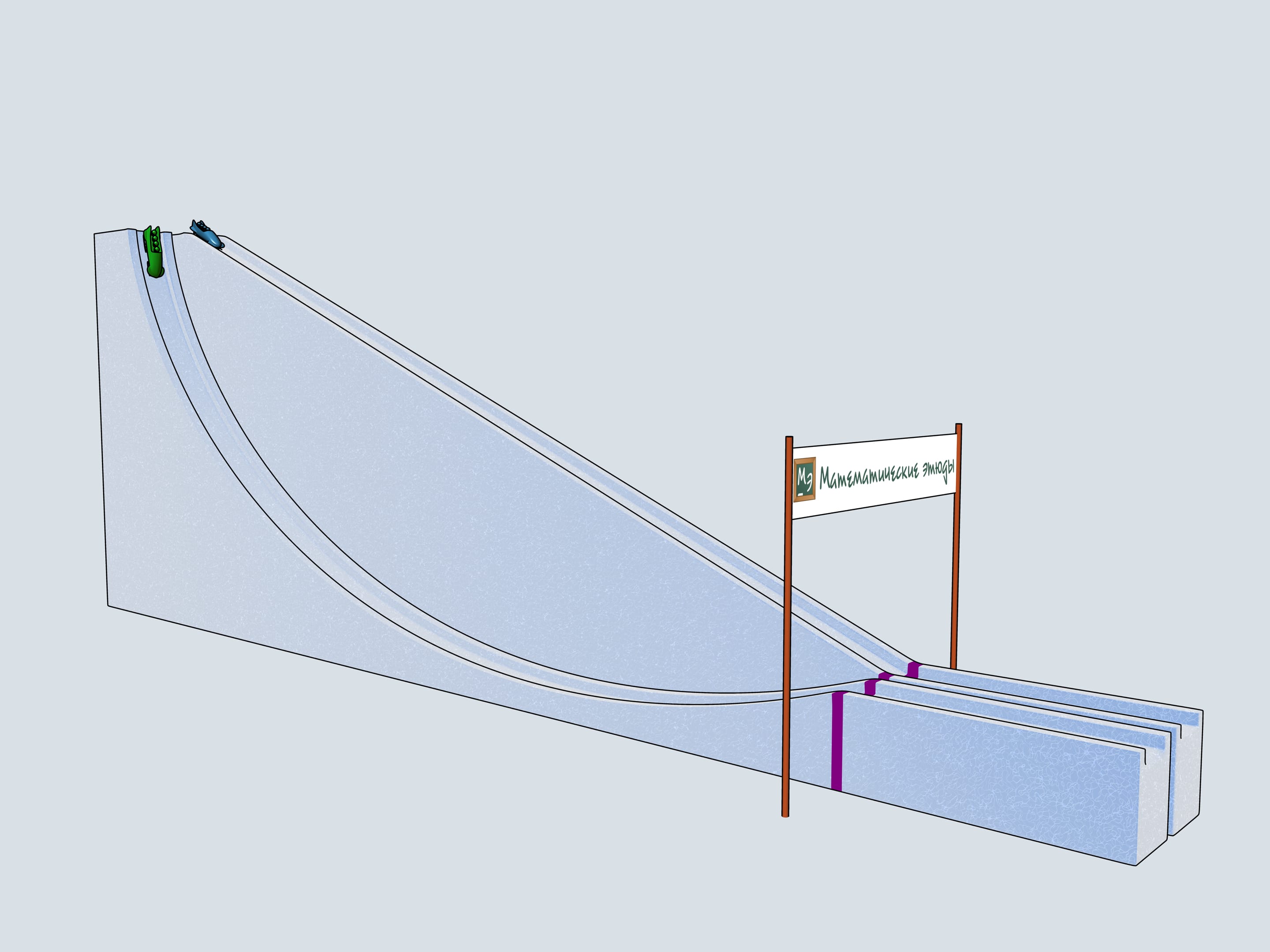
Nous construi­sons trois pistes de bob iden­tique au profil de la cycloïde, de sorte que le point le plus bas, à la ligne d’arrivée, coïn­cide avec le sommet de la cycloïde (c’est à dire le point maximal de la cycloïde, avant d’être retournée). Posons trois trai­neaux à trois hauteurs diffé­rentes et donnons le départ. Fait surpre­nant: les bobs atteignent l’arrivée les trois à la fois!

En hiver, vous pouvez construire un toboggan de glace et véri­fier vous-même cette propriété!

Le problème de la tauto­chrone consiste à trouver une courbe de façon que, à partir de n’importe quel point de celle–ci, le temps de descente jusqu’à un point donné est le même.

Chris­tiaan Huygens démontra que la cycloïde est la seule courbe tauto­chrone.

Bien sûr, Huygens ne s’inté­res­sait pas aux descentes sur la glace. A cette époque, les scien­ti­fiques ne connais­saient pas le luxe de s’occuper de sciences pour plaisir. Les problèmes venaient de tenter de résoudre les problèmes tech­niques de leur temps. Au XVIIe siècle on faisait déjà de longs voyages en mer. C’est surpre­nant que les marins savaient comment définir la lati­tude assez préci­sé­ment, mais ils ne savaient pas vrai­ment comment calculer la longi­tude. Et l’une des méthodes de mesure qui ont été offerts était basée sur la dispo­ni­bi­lité des chro­no­mètres précis.

Le premier savant qui a pensé de construire un pendule exacte a été Galilée Galilei. Cepen­dant, à cette époque, quand il a commencé à le construire, le scien­ti­fique était déjà vieux, presque aveugle et ne réussit pas, dans la dernière année de sa vie, à construire l’horloge. Il confia son projet à son fils, mais celui–ci n’a commencé à s’occuper du pendule que juste avant sa mort, sans être en mesure de réaliser le projet. Le savant qui réussit enfin à réaliser le projet d’un pendule exacte fut Chris­tiaan Huygens.

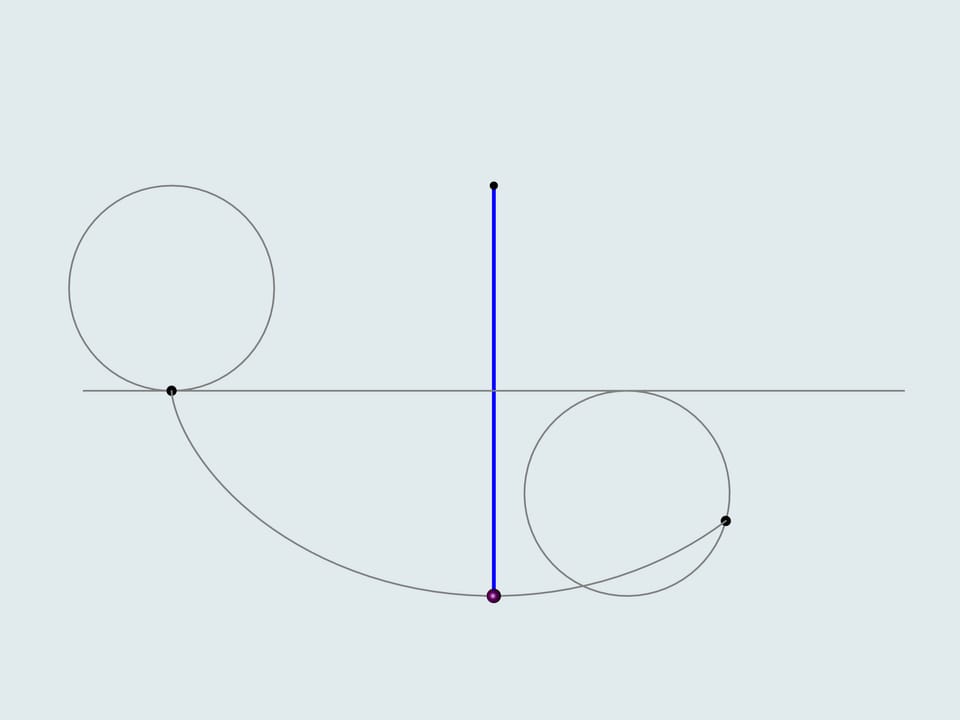
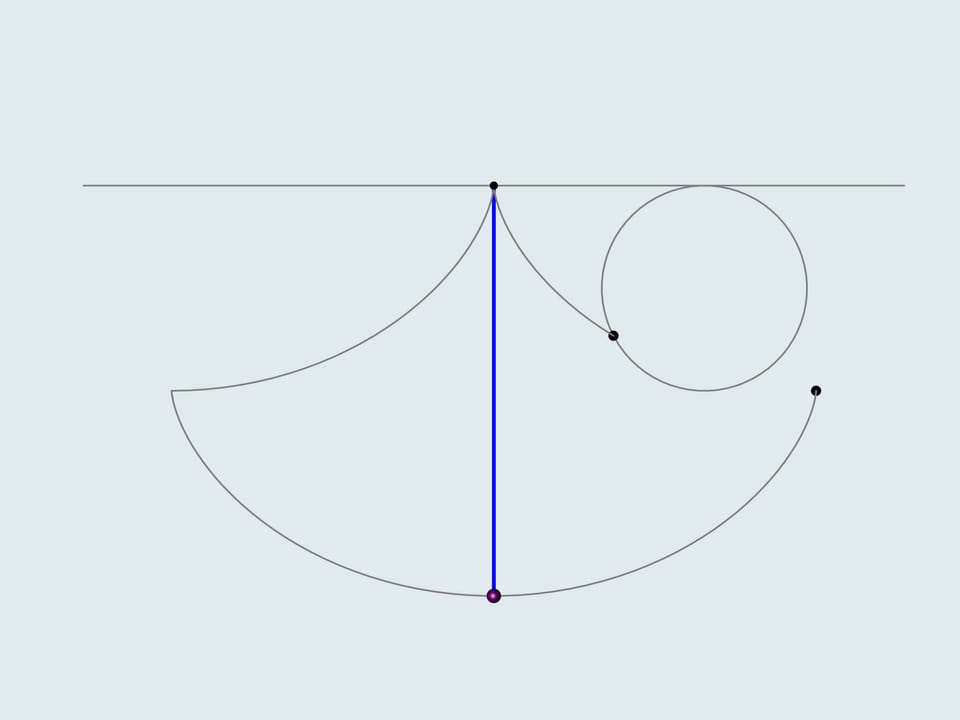
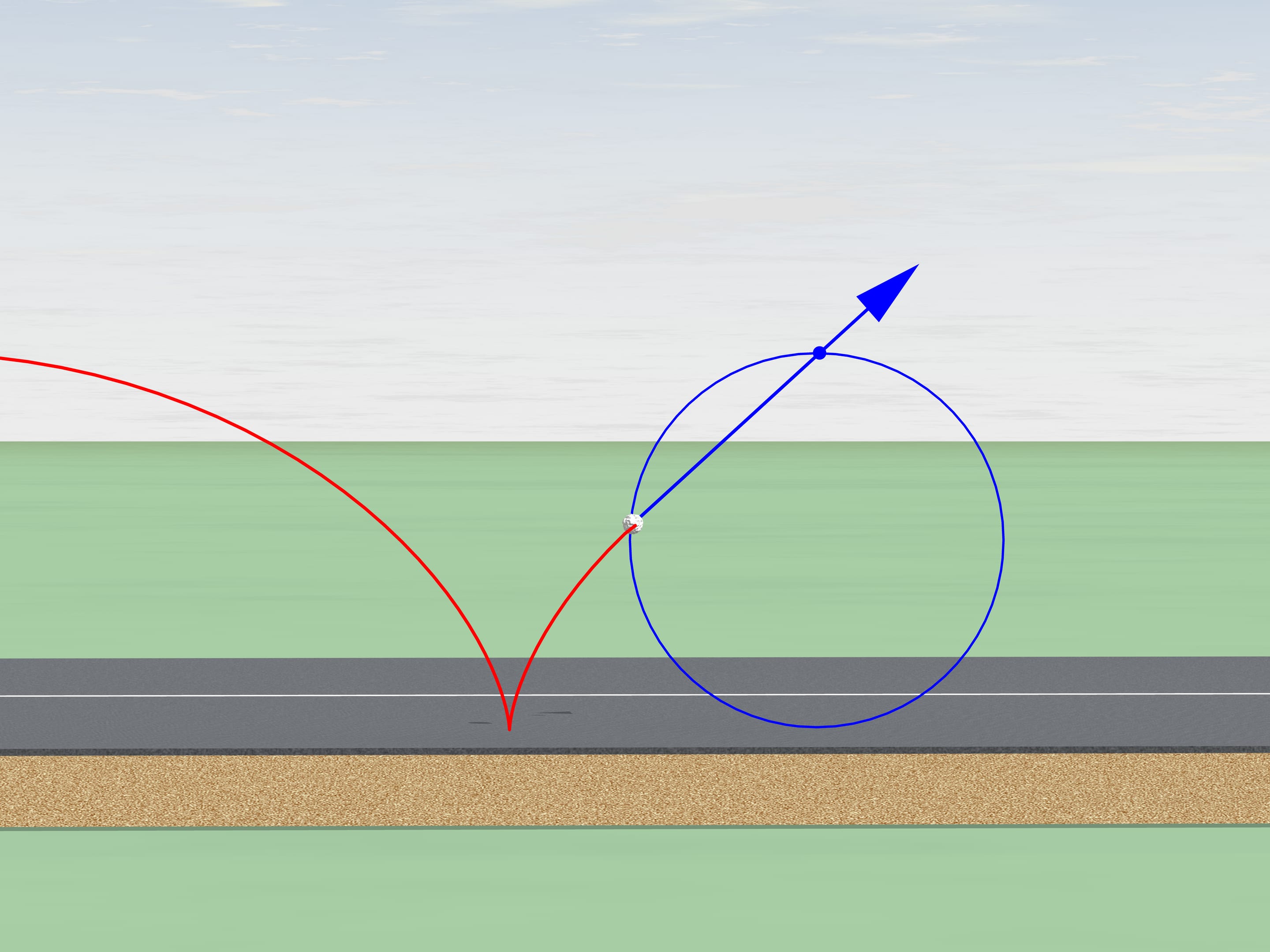
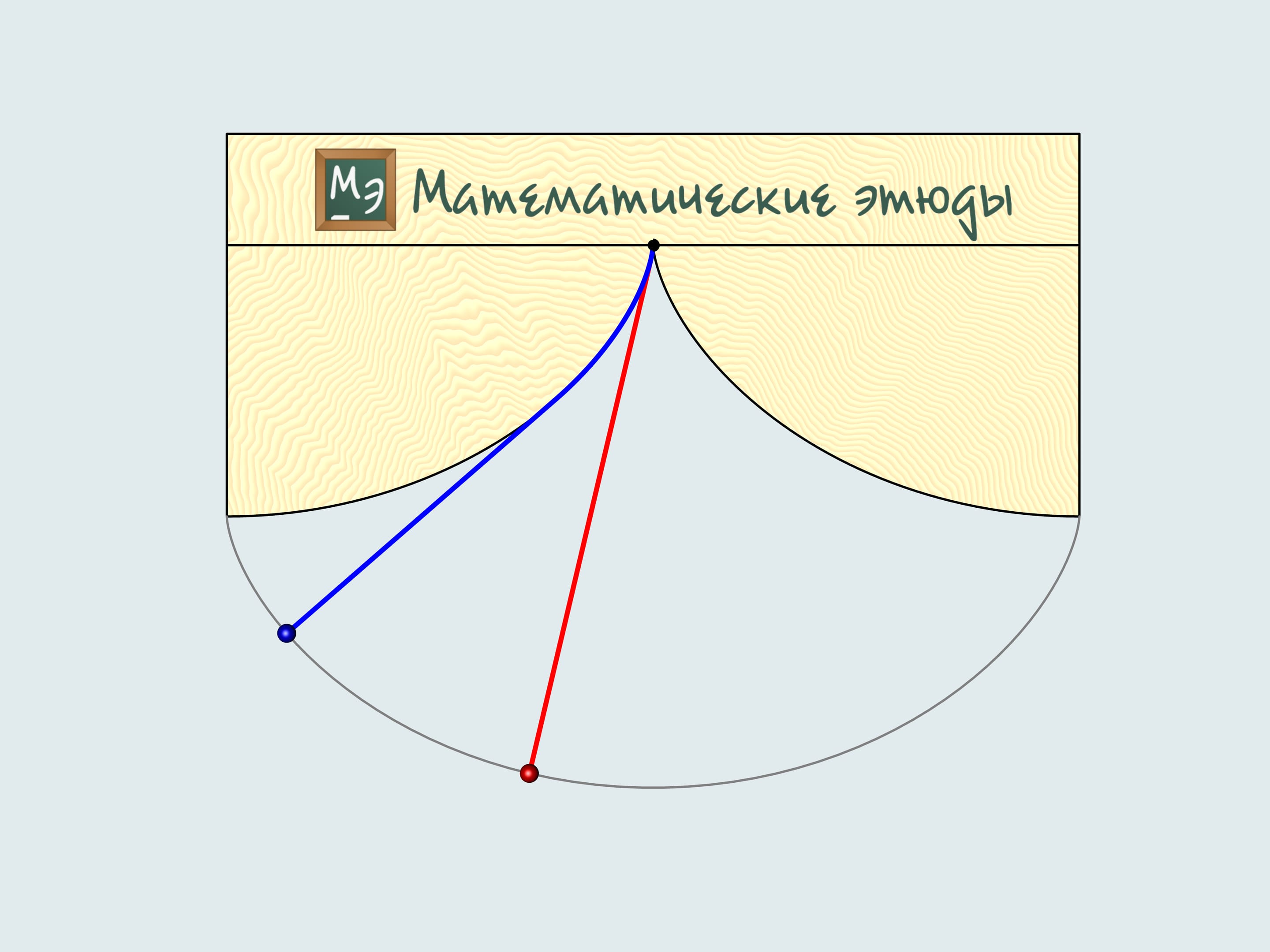
Il remarqua que la période d’oscil­la­tion d’un pendule commune, tel que Galilée l’avait observé, dépend de la posi­tion initiale, c’est–à–dire, de l’ouver­ture de l’angle. En cher­chant la courbe sur laquelle la trajec­toire du mouve­ment du poids devrait se déve­lopper, de sorte que la période d’oscil­la­tion le long d’elle ne dépend pas de l’ouver­ture, il résolut le problème de la tauto­chrone. Mais comment pouvons–nous accro­cher un poids et arriver à le faire osciller le long d’une cycloïde? Tradui­sant en pratique les résul­tats obtenus en théorie, Huygens construit deux “côtés”, sur lesquels la corde du pendule s’enroule. Il résolut de cette manière d’autres problèmes mathé­ma­tiques. Il montra que les profils des “côtés” doivent être eux–mêmes des cycloïdes, démon­trant que la courbe évolué d’une cycloïde est encore une cycloïdes e avec les mêmes para­mètres.

En outre, la construc­tion du pendule cycloïdal proposé par Huygens permet de calculer la longueur de la cycloïde. Si la corde, dont la longueur est quatre fois le rayon du cercle géné­ra­teur de la cycloïde, est toute repo­sant sur le côté, son extré­mité est située à la jonc­tion entre le profil du côté cycloïdal avec la trajec­toire. Ce point est le sommet de la cycloïde, profil du côté. Puisque ce profil est la moitié d’un arc entier de la cycloïde, la longueur de la cycloïde (entre deux points cuspi­daux) est huit fois le rayon du cercle géné­ra­teur.

Chris­tiaan Huygens construisit en fait le pendule cycloïdal, et avec lui une montre. Son fonc­tion­ne­ment a été testé en mer, mais à la fin n’obtint pas succès.

Mais pourquoi il y a encore des méca­nismes d’horloges à pendule? Si vous prêtez atten­tion, alors pour de petites oscil­la­tions, (comme le pendule rouge dans la figure), les "côtés" du pendule cycloïdal n’ont presque aucune influence. Par consé­quent, pour petites ampli­tudes, le mouve­ment le long de la cycloïde, et celui le long de la circon­fé­rence sont quasi­ment iden­tiques.