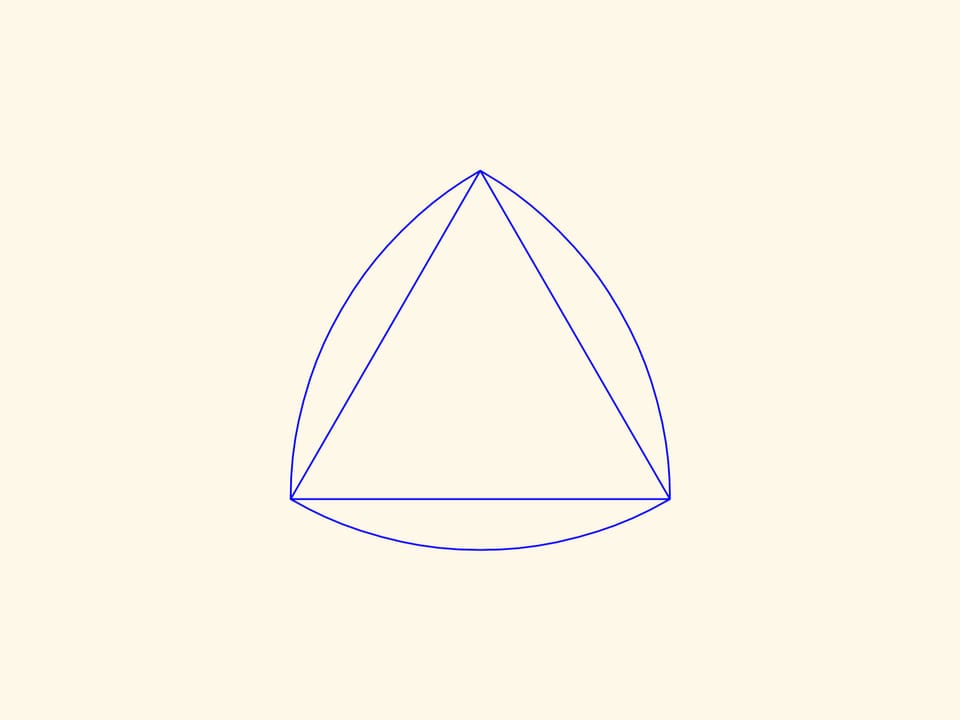
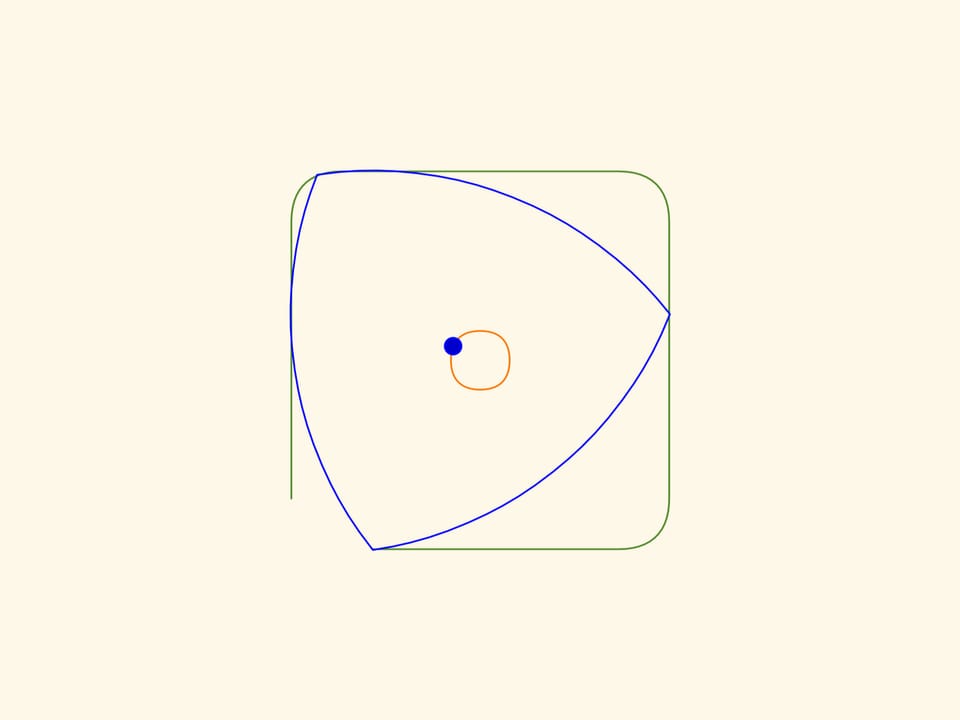
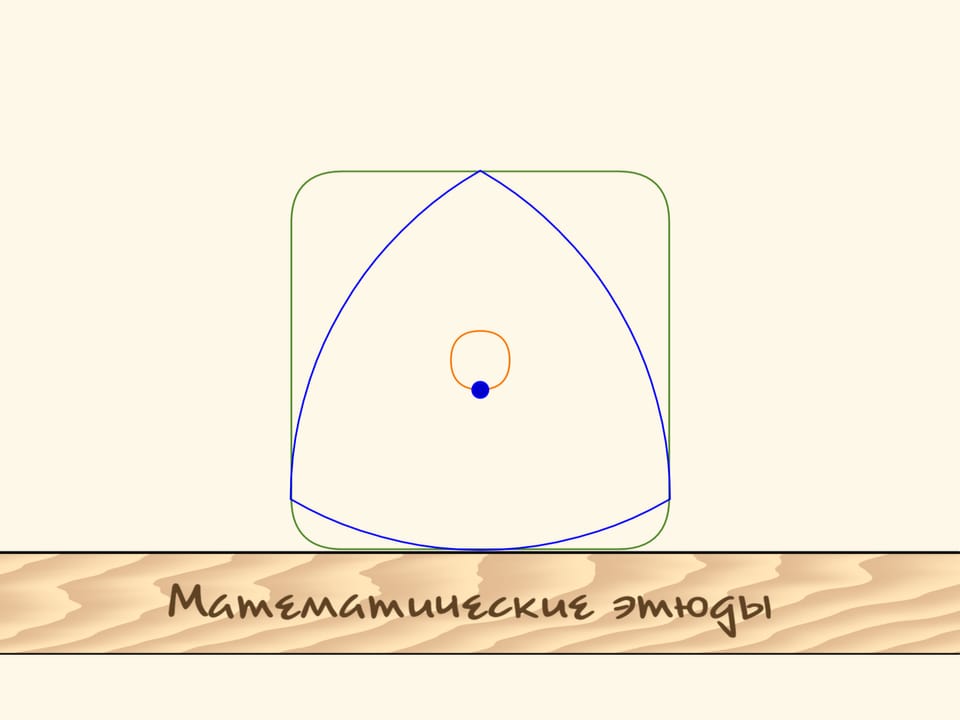
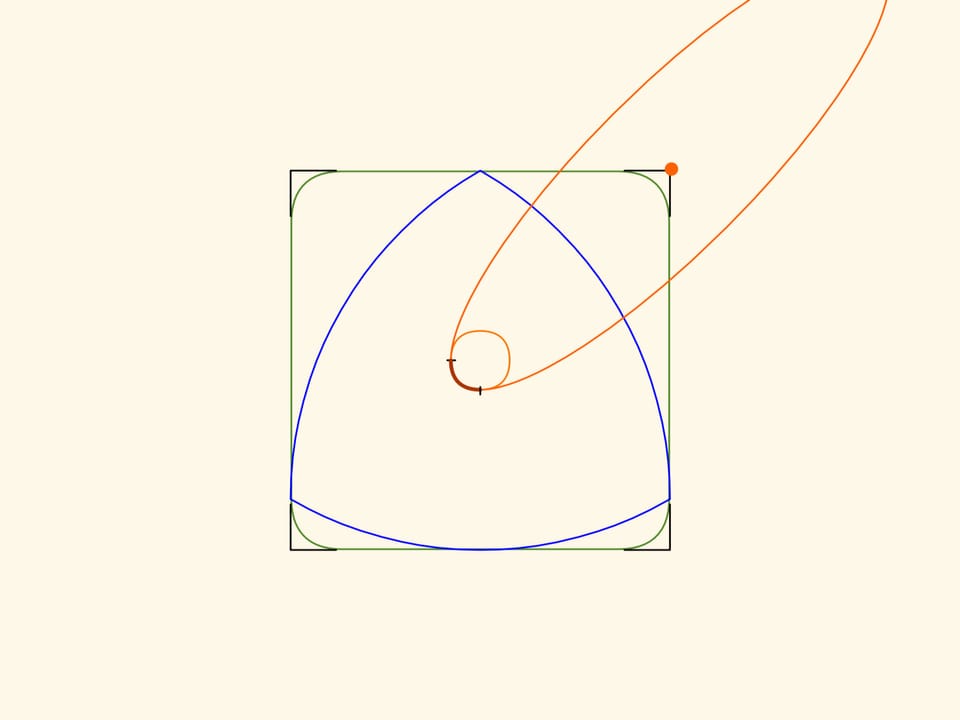
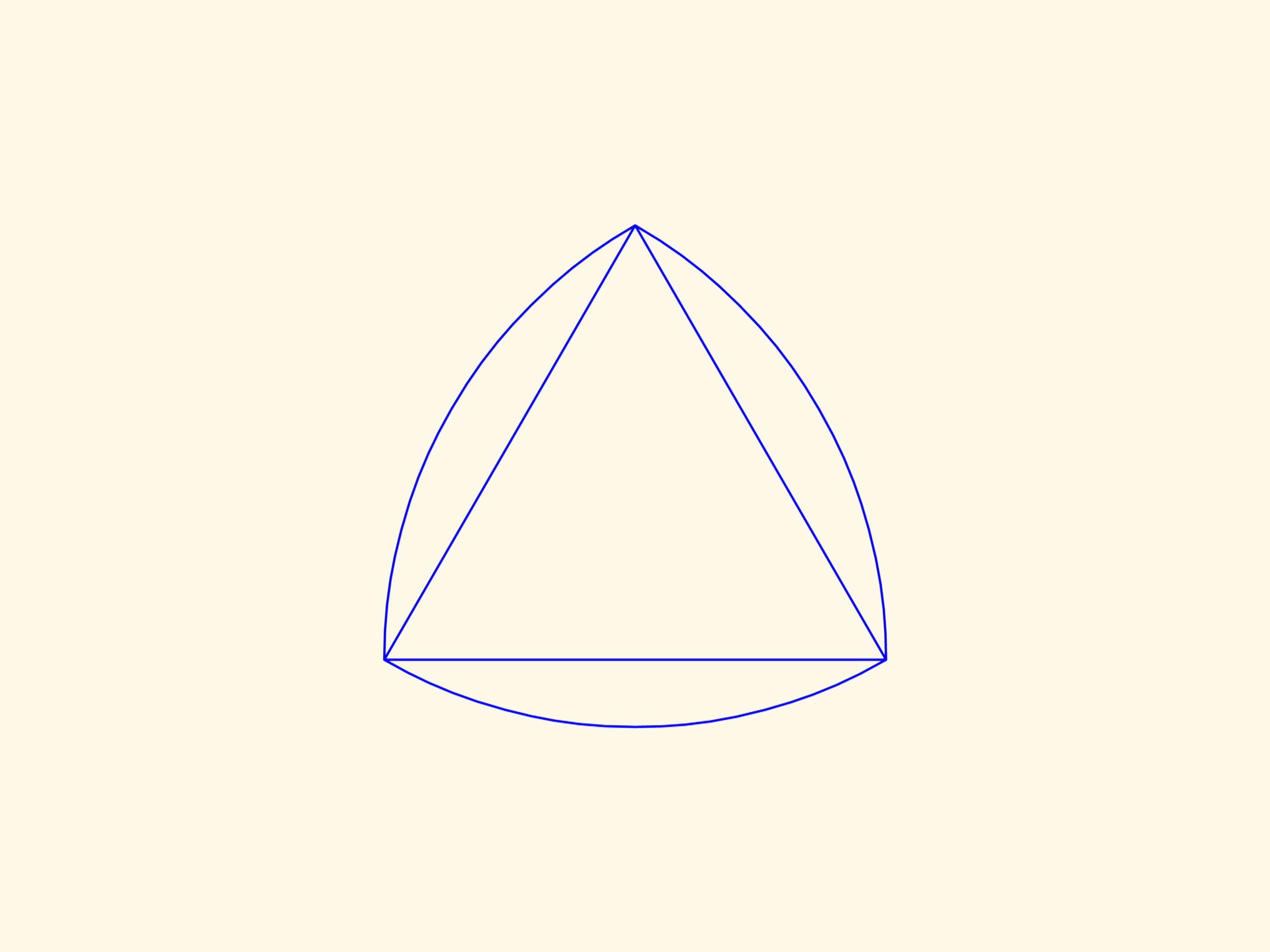
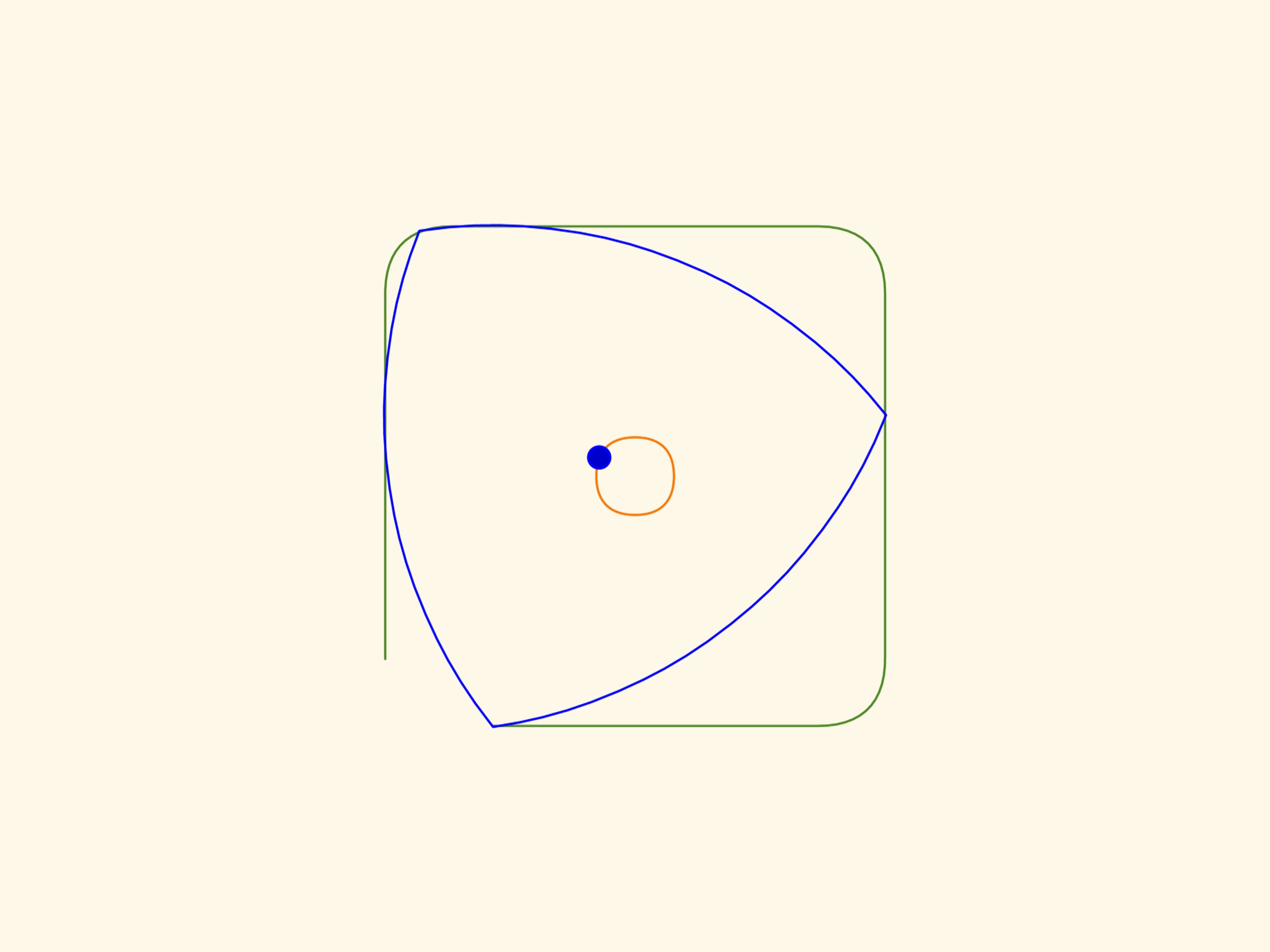
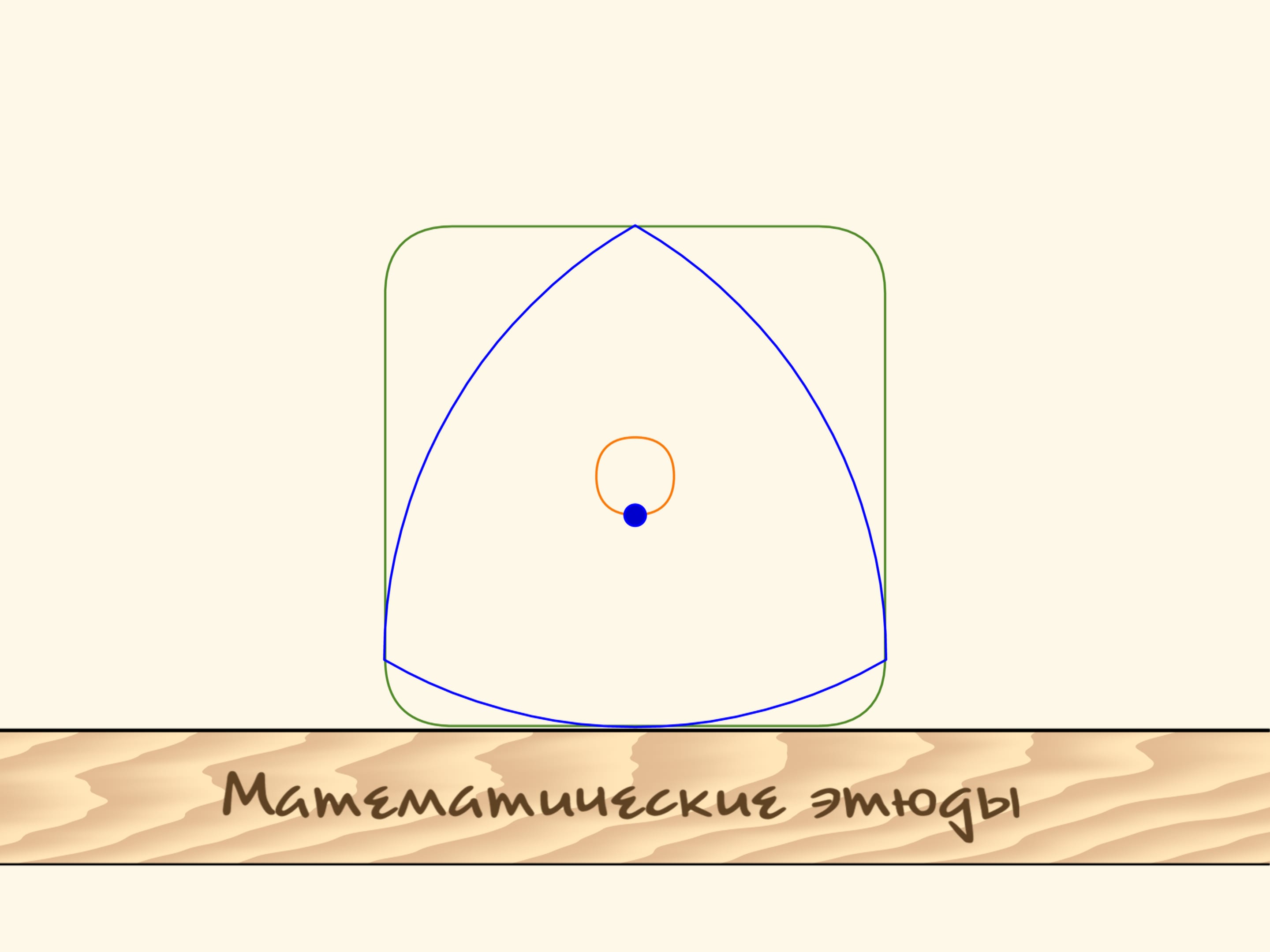
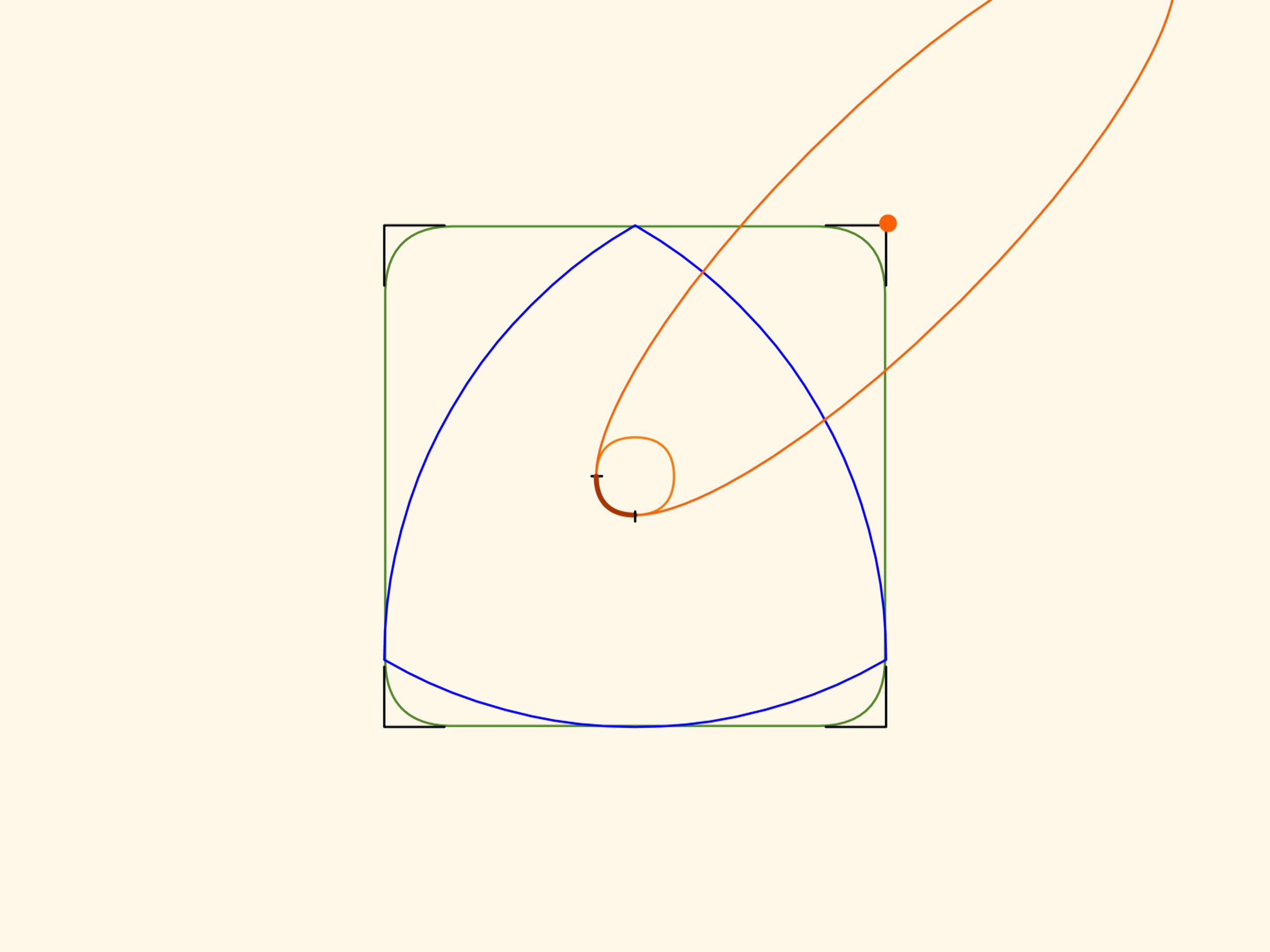
Dans le film Le triangle recourbé de Reuleaux nous avons vu des figures qui ont une largeur constante. Que le triangle de Reuleaux est la plus simple de ces figures nous aidera à réaliser des trous carrés. Si vous déplacez le centre de ce «triangle» le long d’une certaine trajectoire, son sommet dessinera presque un carré et le triangle même couvrira, en balayant, toute la surface à l’intérieur de la figure ainsi obtenue.
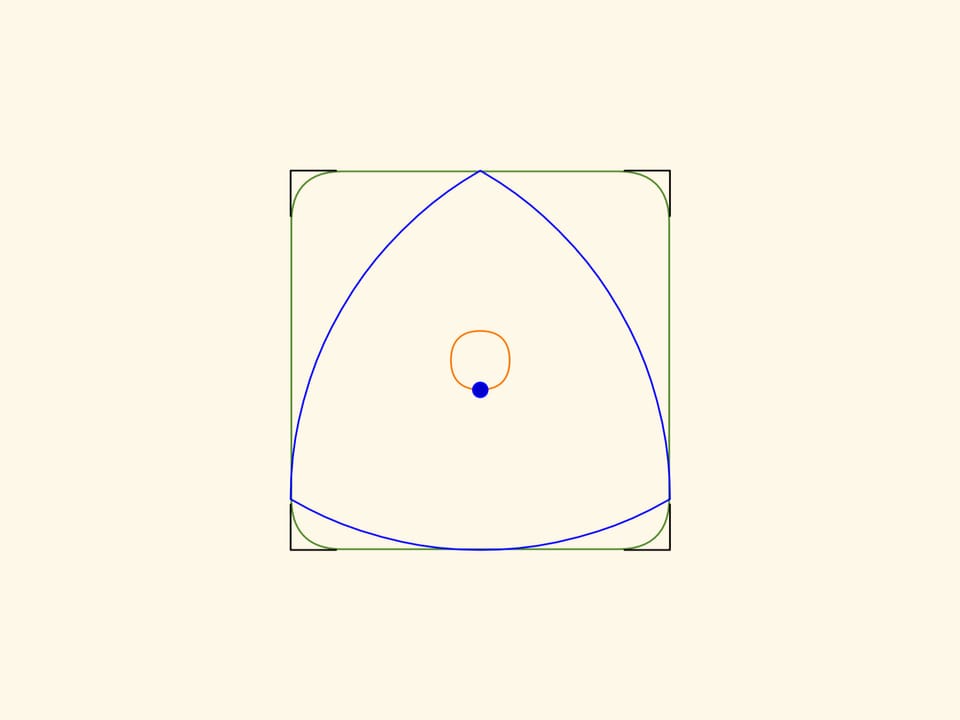
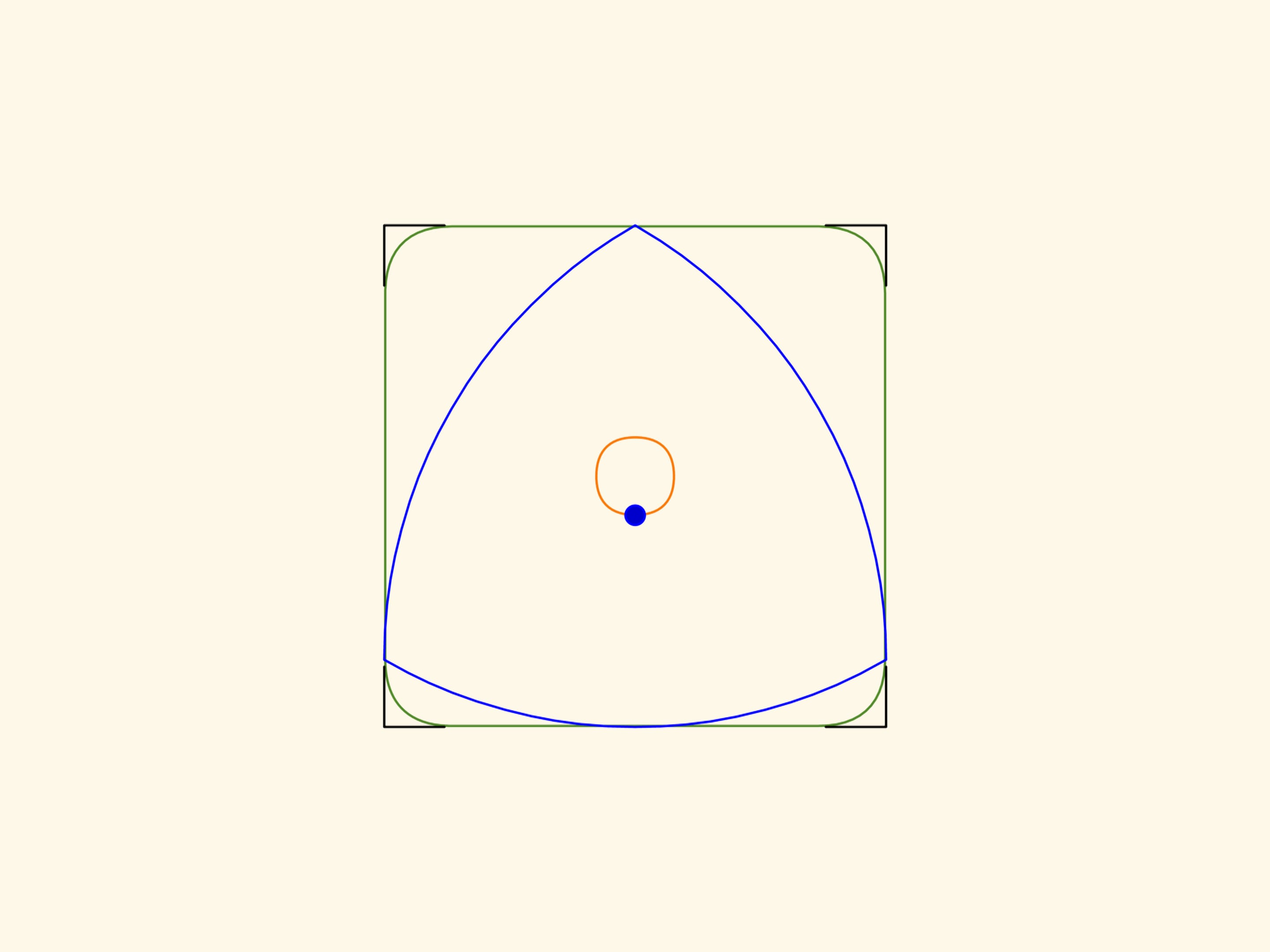
Les côtés de cette figure, à l’exception de petits morceaux au coins, seront strictement rectilignes! Et en prolongeant ces segments de droites on obtiendra exactement un carré.
Afin de réaliser ce que nous avons décrit, le centre du triangle de Reuleaux doit se déplacer le long d’une trajectoire, qui est l’union de quatre arcs égaux d’ellipses. Les centres des ellipses sont situées sur les sommets du carré tandis que les demi–axes sont inclinés de $45^\circ$ par rapport aux côtés du carré, et ont longueur égale à $k\cdot(1+1/\sqrt{3})/2$ et $k\cdot(1-1/\sqrt{3})/2$, $k$ étant la longueur du côté du carré.
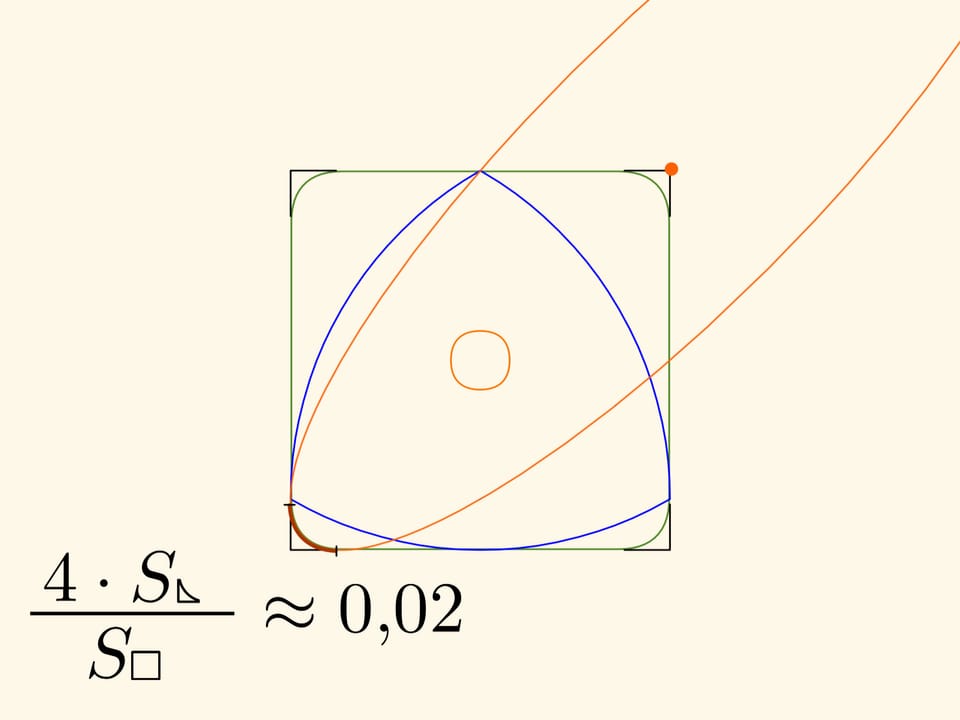
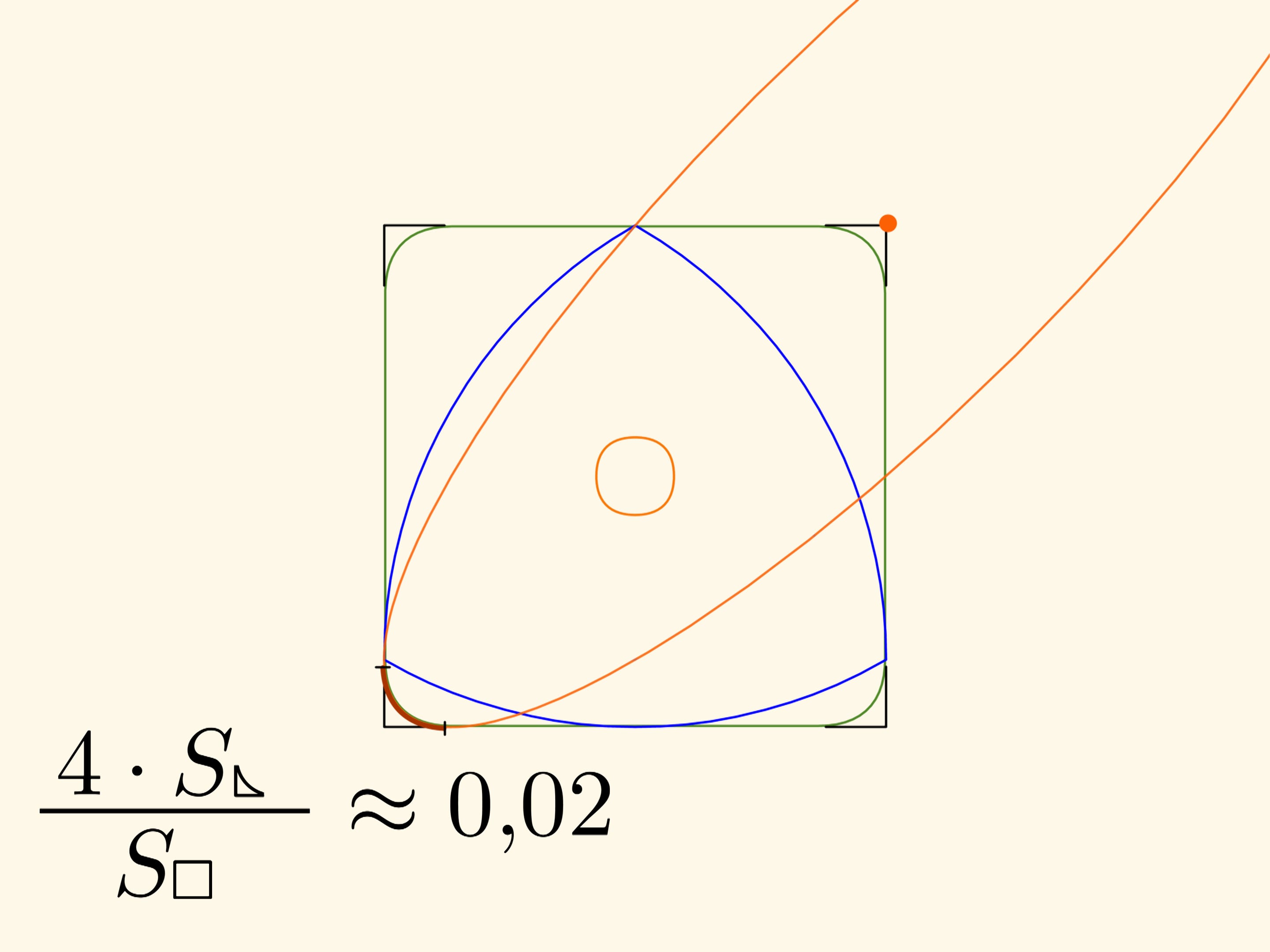
Les morceaux de courbe qui remplacent les coins aux angles droits sont également des arcs d’ellipses avec leur centres aux sommets du carré, inclinés de $45^\circ$ par rapport aux côtés du carré, et ayant longueur égale à $k\cdot(\sqrt{3}+1)/2$ et $k\cdot(\sqrt{3}-1)/2$ respectivement.
La surface aux coins qui est exclue est à peu près le 2 pour cent de toute le carré!
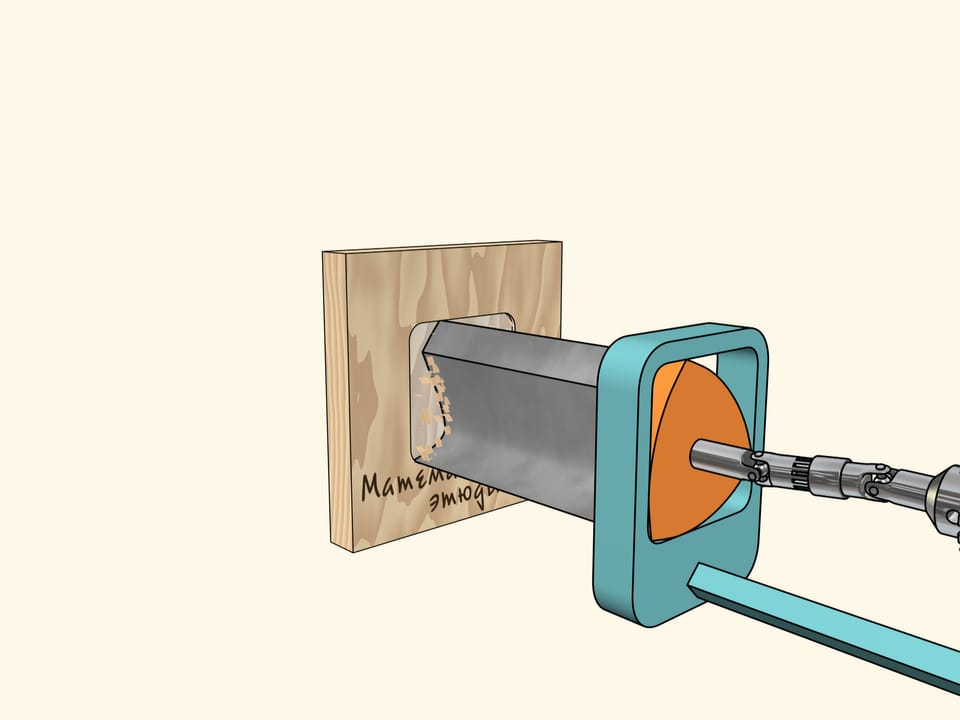
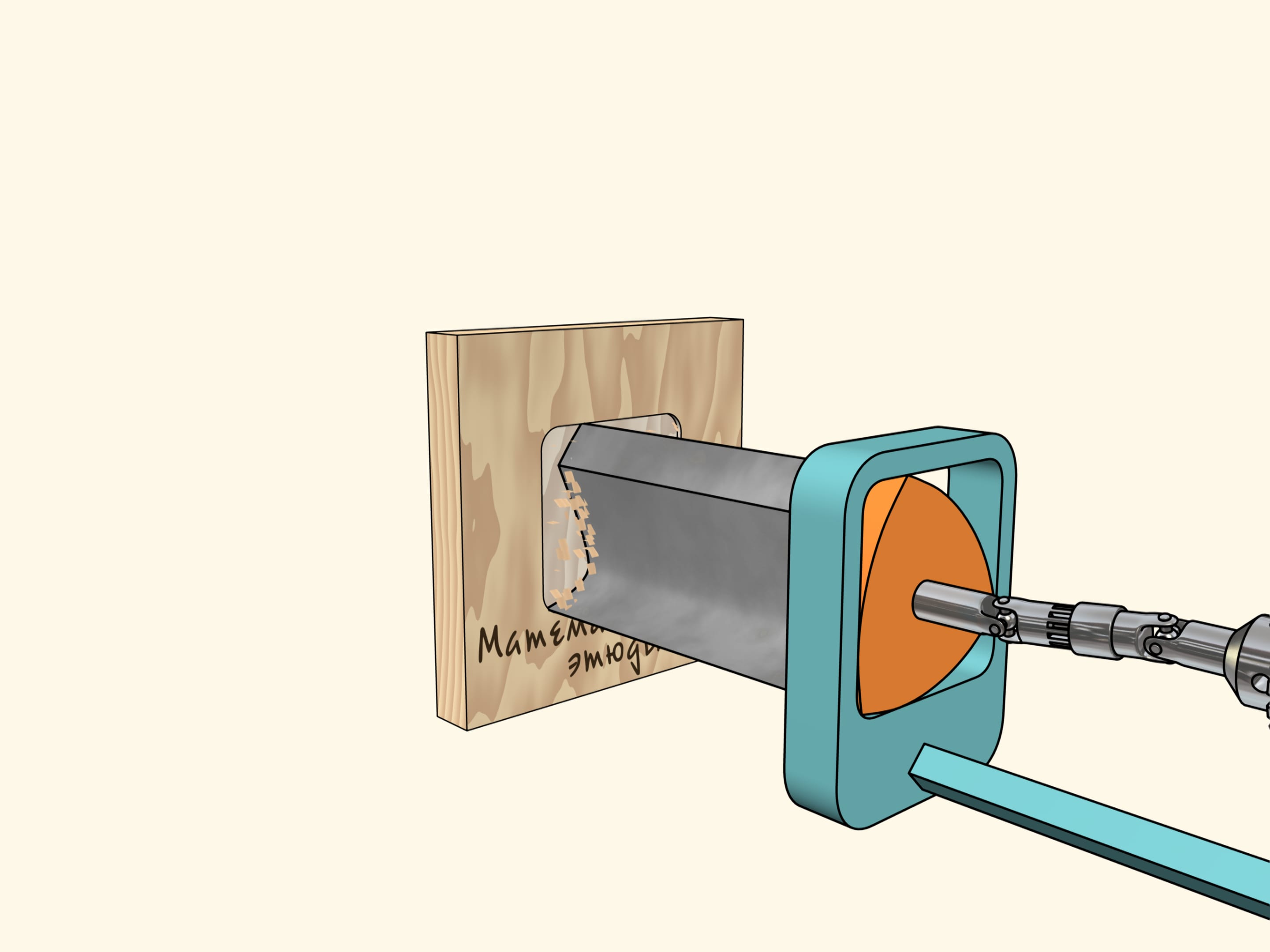
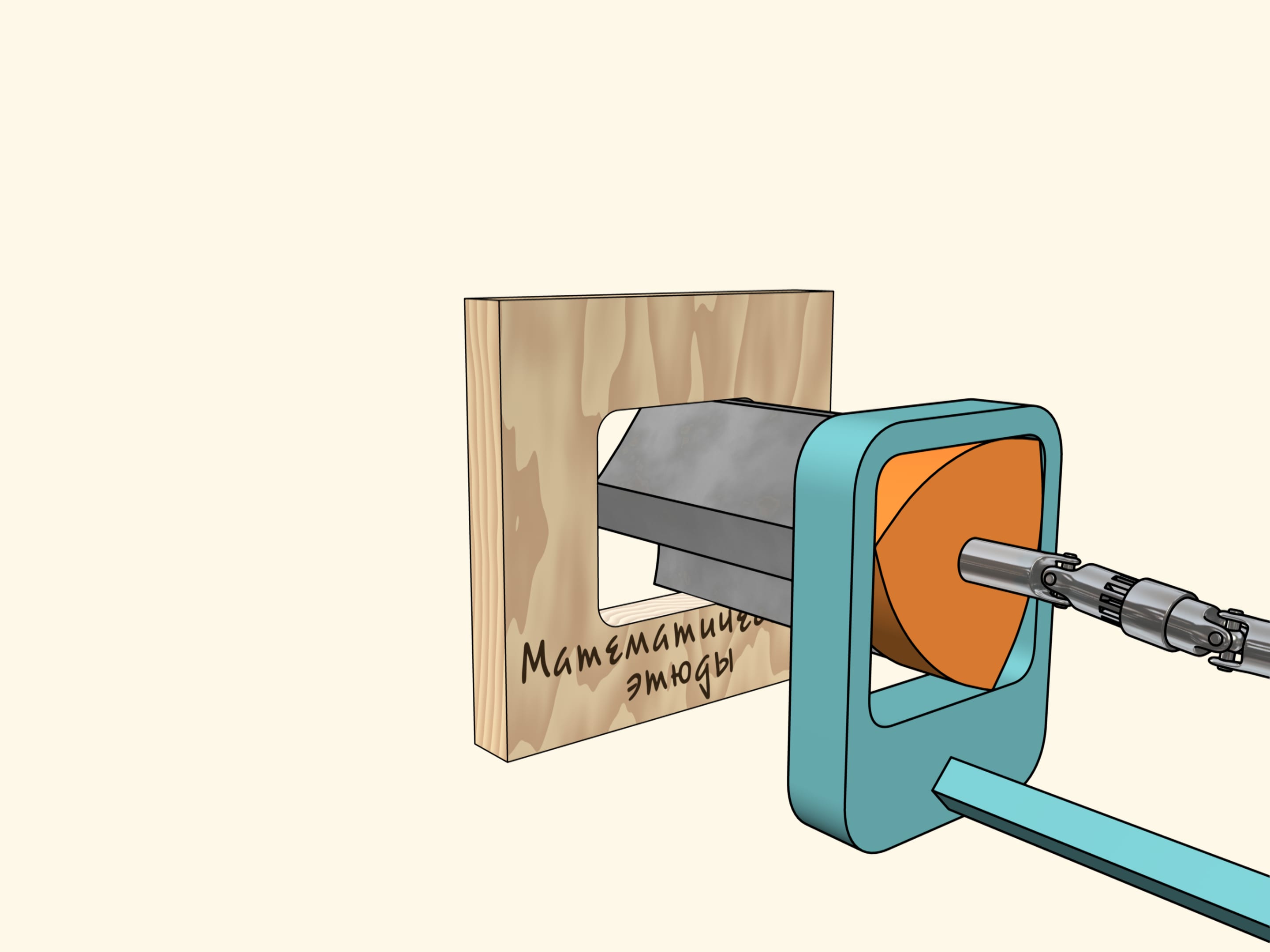
Si maintenant vous avez le foret d’une perceuse ayant la forme du triangle de Reuleaux, alors vous pouvez percer des trous carrés un peu «arrondis» aux coins, mais avec les côtés parfaitement droits!
Il reste à construire une telle perceuse... Ou plutôt, il n’est pas compliqué de construire le foret en soi, il suffit qu’il aie une section similaire au triangle de Reuleaux, avec les arêtes vives en correspondance des sommet du triangle.
La seule difficulté est, comme indiqué précédemment, que la trajectoire du centre du triangle doit être composé de quatre arcs d’ellipses. A vue de nez, cette courbe ressemble beaucoup à un cercle, et même mathématiquement est très proche de lui, mais ce n’est pas un cercle, tandis que toute excentrique (obtenue par un cercle dont le centre se déplace sur un autre cercle de rayon différent) utilisée dans les mécanismes techniques, donne un mouvement qui est strictement circulaire.
En 1914, l’ingénieur britannique James Harry Watt invente un moyen de surmonter cette difficulté. Sur une surface on a découpée la forme d’un carrée, dans laquelle le foret de la perceuse se déplacera. Ce foret est libre de se déplacer dans le porte–foret, afin de couvrir toute la surface en dedans du contour. L’usine, qui a obtenu le brevet pour ce mécanisme, a commencé à produire les perceuses Watts en 1916.
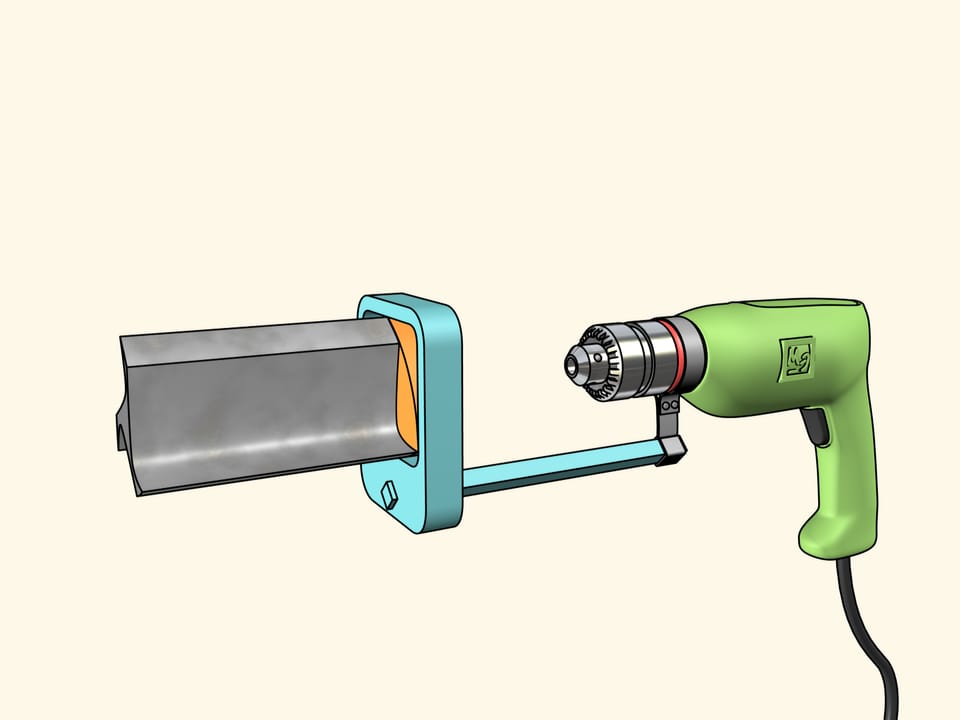
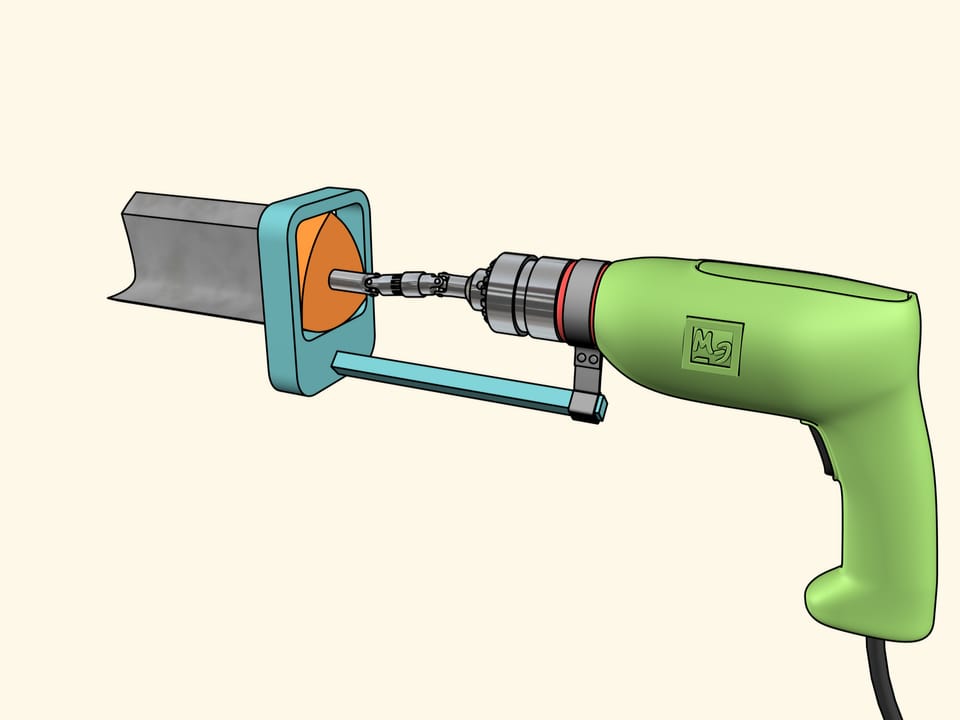
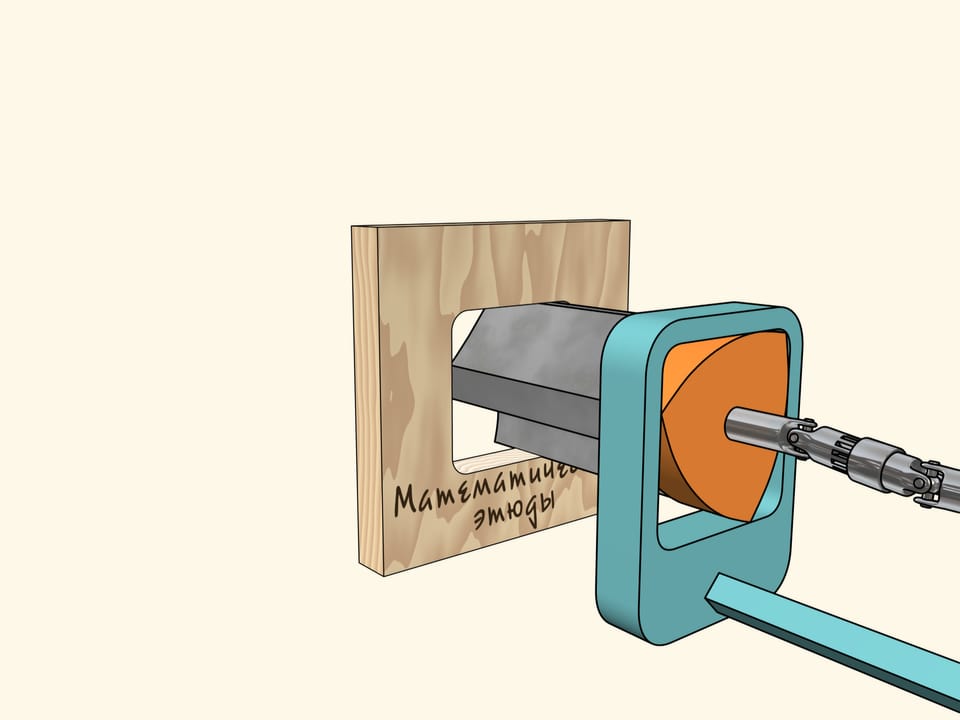
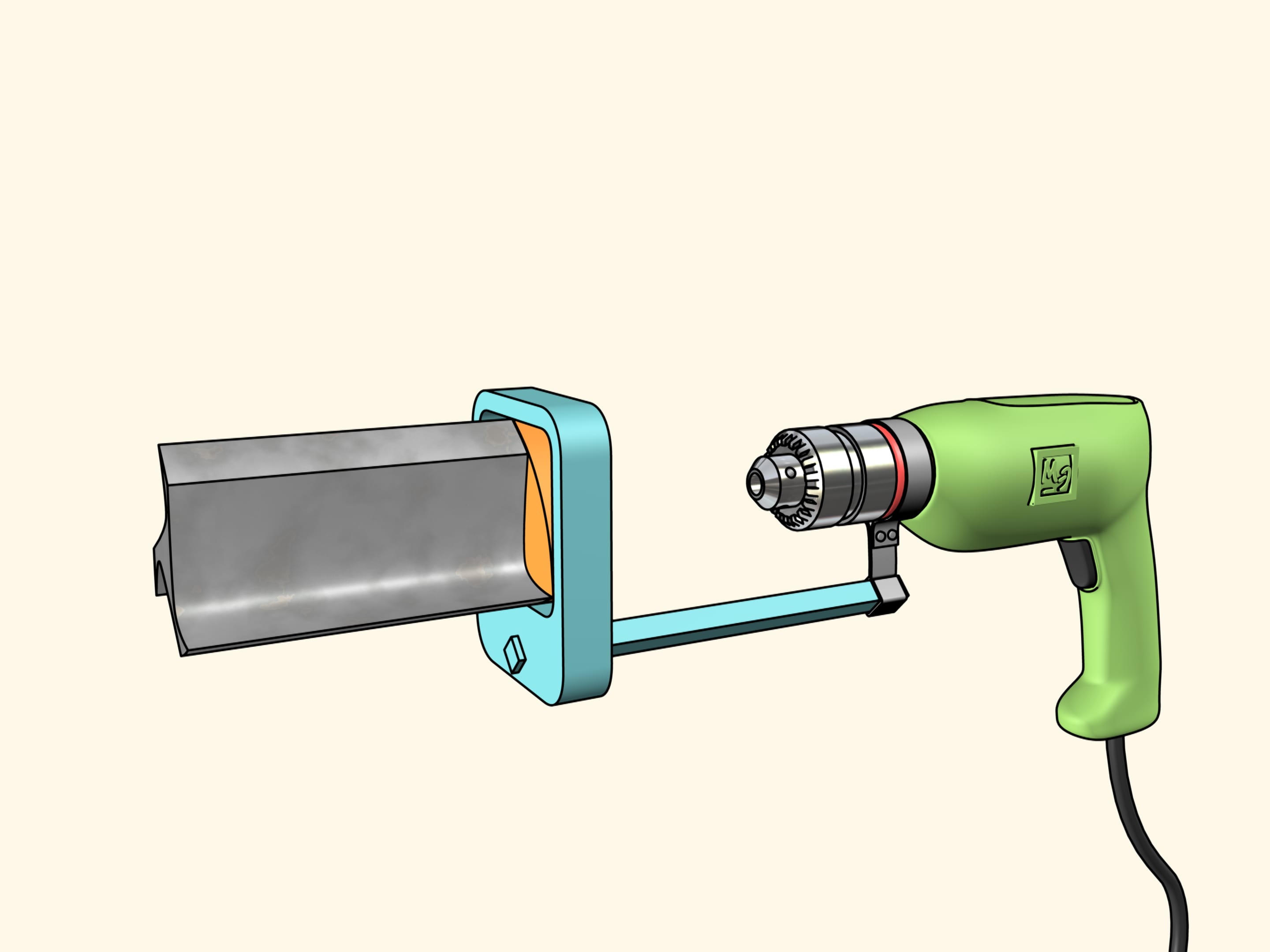
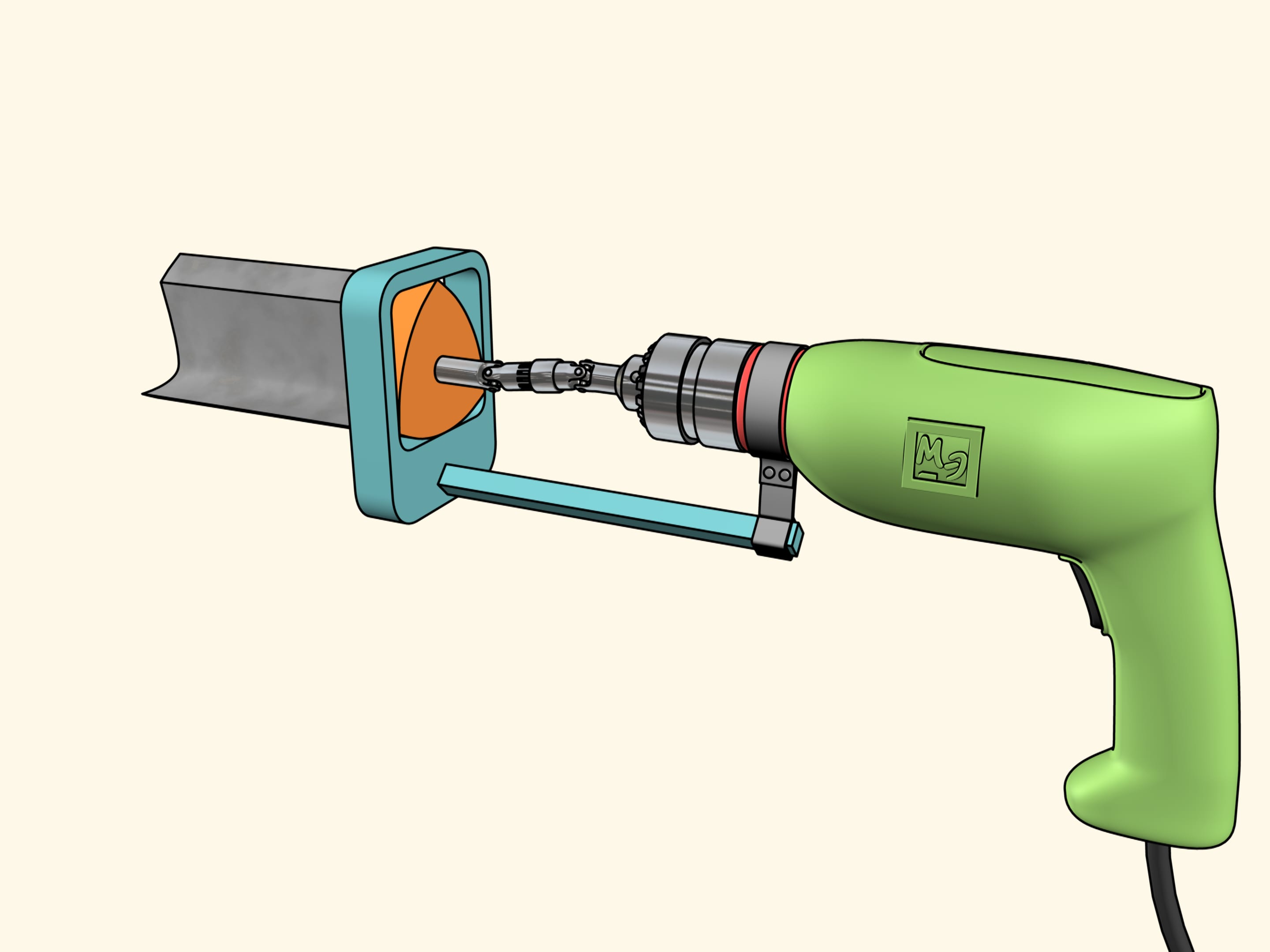
Nous allons utiliser une autre construction. Nous avons fixé le foret au triangle de Reuleaux qui se déplace dans un cadre carré qui sert de guide. Le cadre lui–même est fixé à la perceuse. Maintenant, nous devons faire tourner le triangle de Reuleaux.
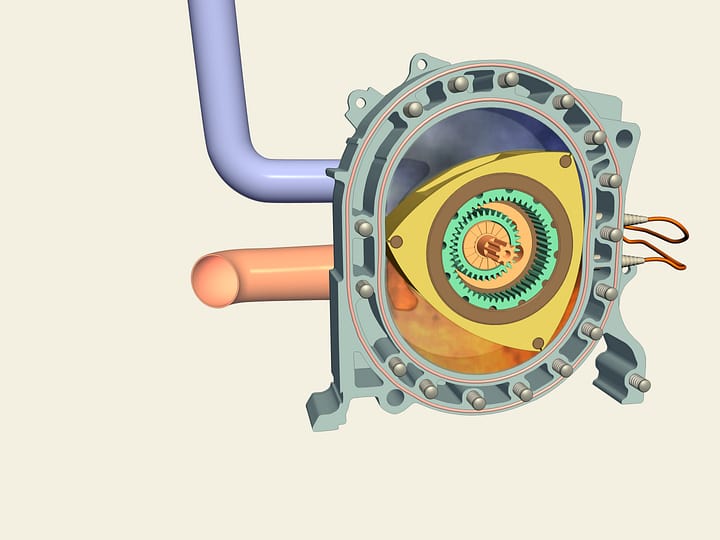
Ce problème technique est résolu avec l’aide d’un dispositif mécanique que vous avez probablement déjà vu de nombreuses fois dans les articulations qui connectent le remorque au camion. C’est le joint de Cardan. Cette articulation est nommé d’après l’inventeur, Jérôme Cardan.
Jérôme Cardan 1501—1576
S. G. Gindikin, Contes de Physique et Mathématiques.
Maintenant tout est prêt pour le forage. Prenons une feuille de contreplaqué et faisons un trou carré! Comme nous l’avons déjà dit, ses côtés seront parfaitement droites, et seuls les coins seront un peu arrondi. Si nécessaire, nous pouvons les corriger par une lime.