Albrecht Dürer (1471—1528) a été un grand artiste allemand. Il s’occupait de questions théoriques concernant les arts et, en particulier, a étudié le problème de la perspective. Une partie de son livre de l’année 1525 «Instructions pour l’art de mesurer les figures dans le plan et dans l’espace en utilisant règle et compas» est dédié à l’étude des propriétés des objets géométriques, y compris les polyèdres et leurs développements.
Le développement d’un polyèdre le long des arêtes consiste à choisir des polygones, disposés sur un seul plan sans qu’ils se superposent, et des conditions de collage de ces polygones. Si en coupant un polyèdre d’une certaine manière le long des arêtes, on obtient un seul polygone, en respectant la condition de ne pas avoir de superpositions, alors ce développement est appelé connexe.
Dans les pages de son livre Dürer montre des développements connexes de certains polyèdres, parfois assez compliqués. Il est peu probable qu’il s’est demandé s’il est toujours possible qu’un seul polygone suffit pour représenter le développement d’un polyèdre, mais la proposition qui suit prend son nom. La conjecture de Dürer est de supposer que chaque polyèdre convexe a au moins un développement connexe le long des arêtes.
Mais pour quelle raison les développements des polyèdres ont suscité un intérêt qui dure depuis des siècles? Le fait est que le développement préserve en lui–même la géométrie interne du polyèdre, c’est à dire, les informations qu’un être minuscule, vivant sur la surface du polyèdre et qui n’a pas de possibilité de la quitter, peut obtenir. Dans ces conditions de vie cet être est capable de mesurer la distance entre deux points. Utilisant ses compétences en mathématiques, il pourra aussi définir, par les mesures des distances, les angles entre deux directions, et calculer l’aire d’une surface...
Pour certaines buts, l’utilisation du développement peut être plus «commode» de l’utilisation du polyèdre lui–même. Par exemple, si vous voulez envoyer le modèle d’un polyèdre dans une autre ville, alors vous avez besoin d’expédier un colis. Mais pour envoyer le développement du polyèdre, il suffit d’expédier une lettre. Le destinataire pourra construire le polyèdre lui–même. Si vous pensez que le transport des polyèdres est un procédé rare, détrompez–vous! Nous tous l’utilisons au quotidien, lorsque nous achetons un paquet de lait ou de jus.
La conjecture de Dürer concerne les polyèdres convexes. À ce jour, elle n’a été ni prouvée ni réfutée. Mais si le problème initial n’est pas de solution, il vaut la peine de changer un peu les conditions, essayant de résoudre le problème modifié. Dans notre cas, il est naturel d’étudier la conjecture analogue pour une classe plus large de polyèdres, comprenant aussi les polyèdres non convexes.
Il est facile de construire un polyèdre non convexe à faces pas nécessairement convexes, et qui n’admet aucun développement connexe. Prenons une étoile non convexe comme base et allons construire une pyramide sur elle. Choisissant de façon appropriée les angles de l’étoile et la hauteur de la pyramide, nous pouvons obtenir que même si une seule face latérale est connecté à la base dans le développement, alors cette face se superposera nécessairement à l’étoile. Par conséquent, la base doit être déconnecté de toutes les autres faces et le développement n’est plus connexe.
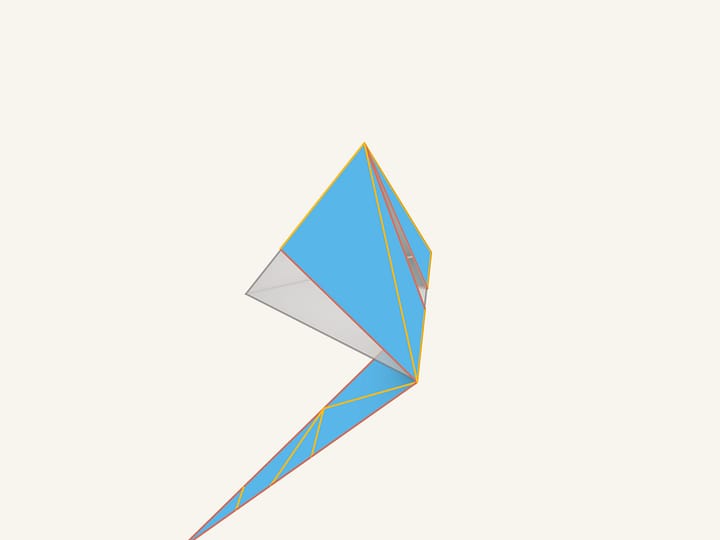
Il n’est pas si facile d’inventer un polyèdre non convexe avec tous les faces convexes et n’ayant aucun développement connexe le long des arêtes. Le premier exemple a été construit seulement en 1999.
Considérons les quatre petits tétraèdres qui sont obtenues en coupant un tétraèdre régulier près de ses sommets. Maintenant on va déformer ces petites pyramides, en gardant leurs bases (fixées au tétraèdre initiale) et éloignant les sommets du centre du tétraèdre; les quatre pyramides régulières résultent allongées. Tous les faces du polyèdre non convexe ainsi obtenu sont des polygones convexes. Si les bases des pyramides sont assez petites par rapport à leurs hauteurs, le polyèdre n’admet pas de développement connexe le long des arêtes. On peut démontrer que si le polyèdre a un développement connexe le long des arêtes, au moins un de ses pointes devrait admettre ce développement, mais ce n’est pas le cas. En fait, considérons une «pointe» avec des morceaux des faces du polyèdre qui lui sont connectés. Tous les développements possibles le long des arêtes de cette partie du polyèdre, constitué d’un seul morceau, auront des superpositions.
Maintenant que nous avons vu un «contrexemple non–convexe» à la conjecture de Dürer, nous revenons à sa formulation initiale, dans la classe des polyèdres convexes.
Le plus simple des polyèdres convexes c’est la pyramide triangulaire (ou tétraèdre), qui a quatre sommets et quatre faces.
Mais même dans cette classe plus simple des polyèdres, il existe de représentants pour lesquels pas tous les développements le long des arêtes sont sans superpositions. Cependant, tous ces représentants admettent des développements connexes. Jusqu’à présent, on n’a pas construit aucun polyèdre, ayant développements le long des arêtes avec superpositions, et constitué d’un seul morceau.
Il n’y a pas longtemps N. P. Dolbinin a formulé une conjecture nouvelle, qu’il a appelé «anti–Durer». Etant donné un entier $k$ arbitraire, il existe un polyèdre convexe tel que, pour que son développement sur le plan le long des arêtes soit sans superpositions, il doit être divisé au moins en $k$ morceaux.
Nous observons que si la conjecture de Dürer est fausse, alors il ya deux cas sensiblement différents.
Le cas borné: pour tout polyèdre convexe il y a un développement sans superpositions constitué au plus de $k$ morceaux. Dans ce cas le nombre $k$ minimale est le même pour toutes les classes de polyèdres convexes, et il ne dépend pas des cas concrets particuliers.
Plus intéressant c’est le cas non borné: dans la classe de tous les polyèdres, le nombre de morceaux nécessaires n’est pas supérieurement borné.
La conjecture «anti–Dürer» consiste seulement à supposer que nous ne sommes pas dans le cas borné.
Récemment, son analogue dans le cas des polyèdres non convexes (dans le cas non borné) a été démontré par des mathématiciens russes.
Vous pouvez essayer de construire un polyèdre convexe, pour lequel tout développement connexe le long des arêtes a des superpositions, ou de démontrer que ce polyèdre n’existe pas. Et, si vous réussissez, une belle nouvelle page sera ajoutée à la géométrie.