Polyèdres flexibles ⁠

S’il vous est arrivé de construire une étagère, alors vous vous souvenez très bien que, jusqu’à ce que vous avez fixé la paroi arrière, l’étagère fléchit. Comme vous ajoutez la paroi arrière, l’étagère, qui devient un poly­èdre pas fermée, devient rigide. Si vous ajoutez ensuite aussi une paroi de façade ou une autre pièce, qui ferme le poly­èdre, l’étagère ne perd pas, bien sûr, sa propriété de rigi­dité.

Y a–t–il des poly­èdres défor­mables?

La réponse à cette ques­tion n’a pas été trouvé pendant une longue période. Comme il arrive souvent en science, pour étudier un problème il convient de consi­dérer un cas plus simple. Dans le cas du problème des poly­èdres défor­mables, il s’agit de regarder le problème pas dans l’espace mais dans le plan, où l’analogue du poly­èdre c’est le poly­gone.

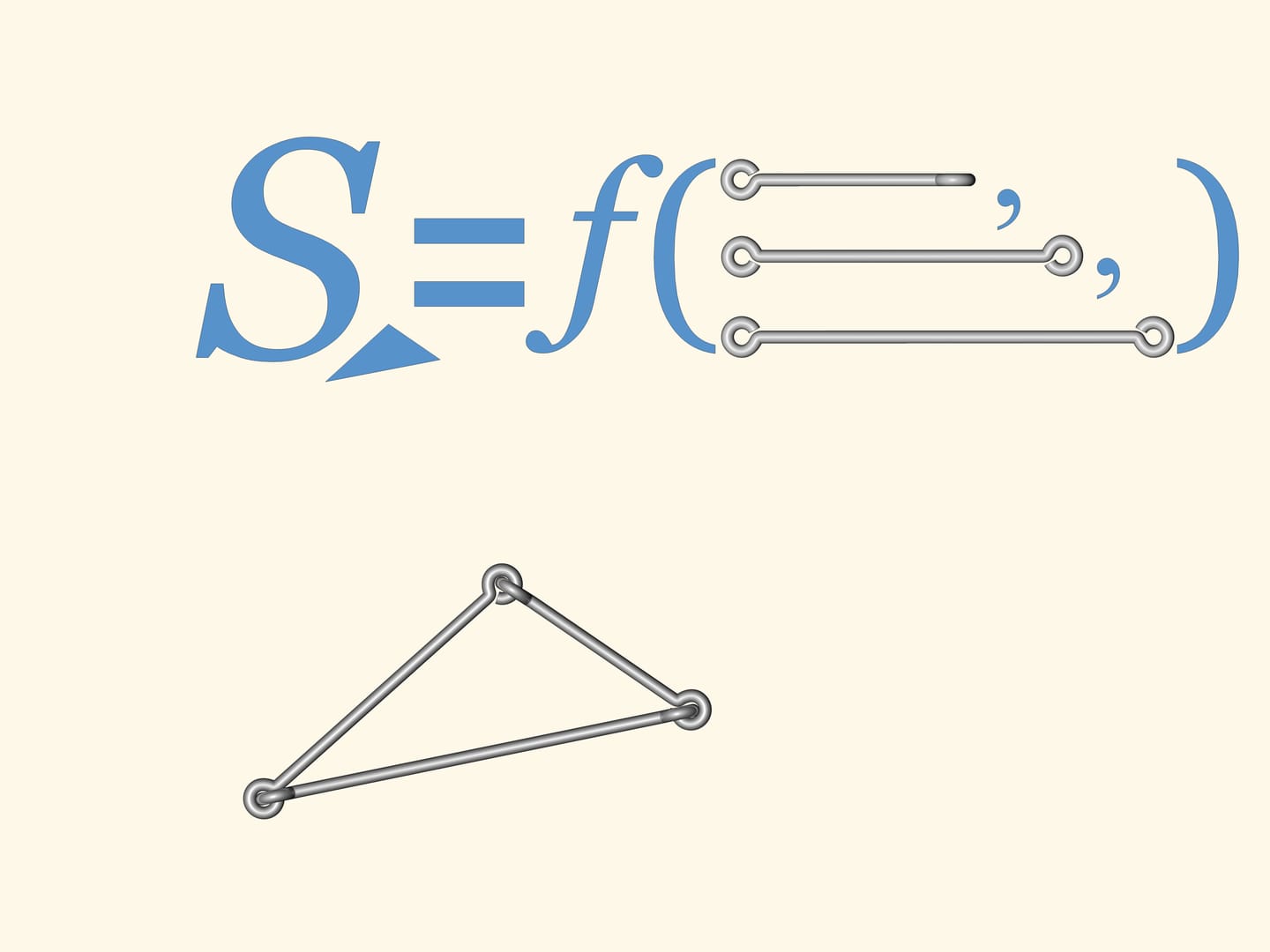
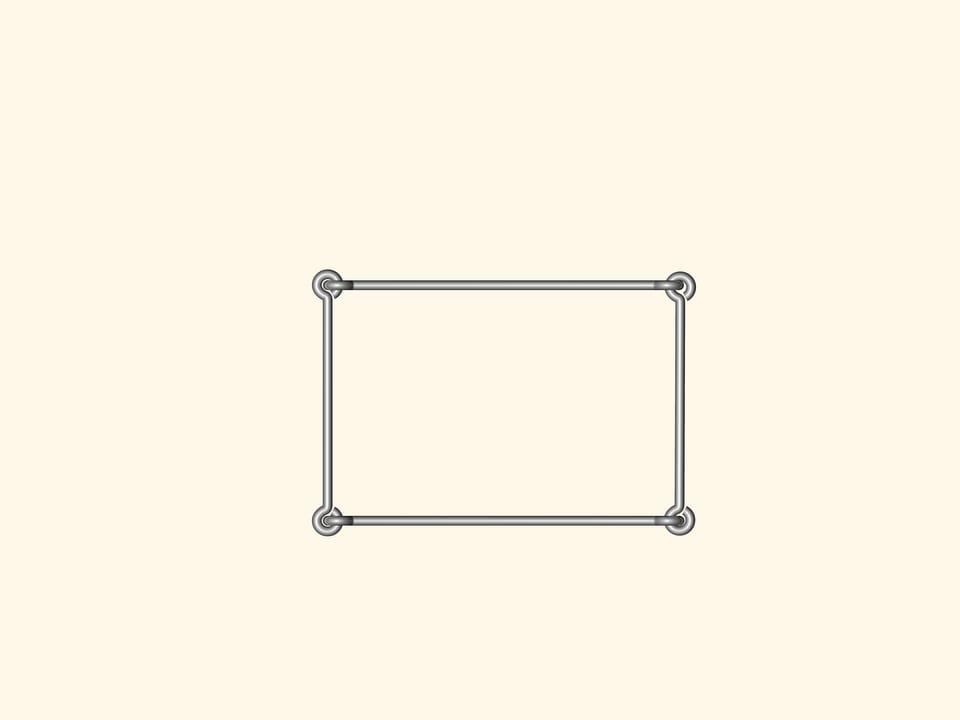
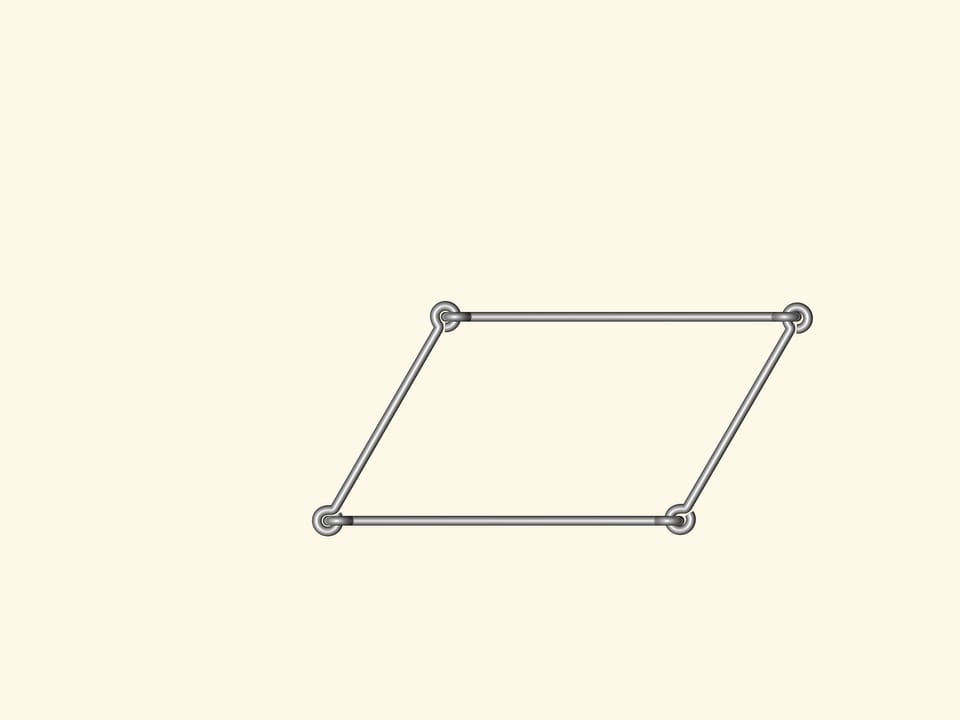
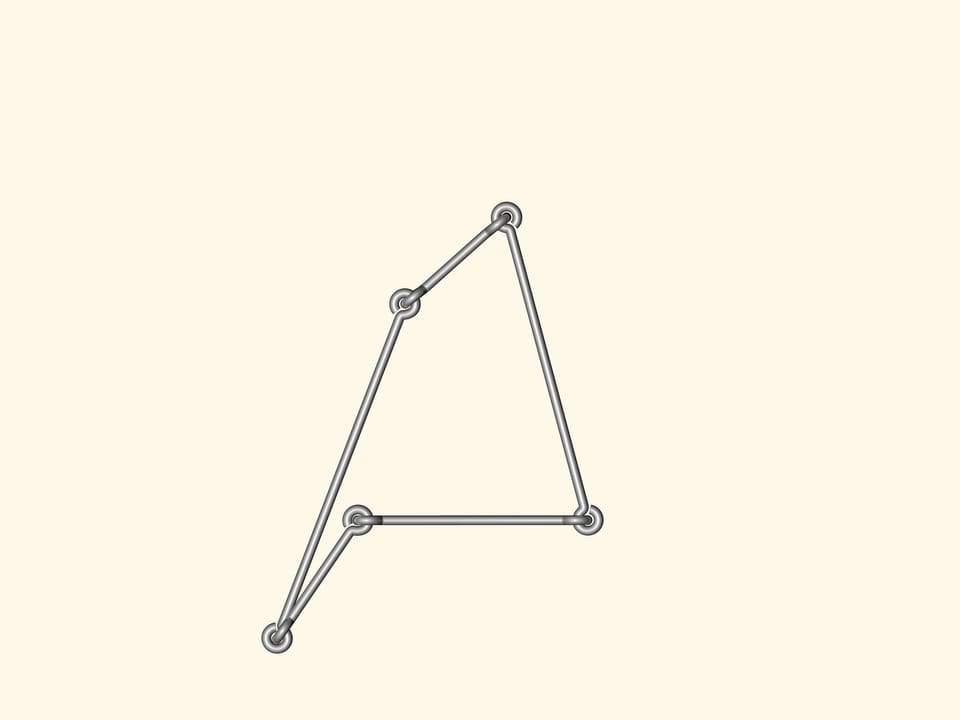
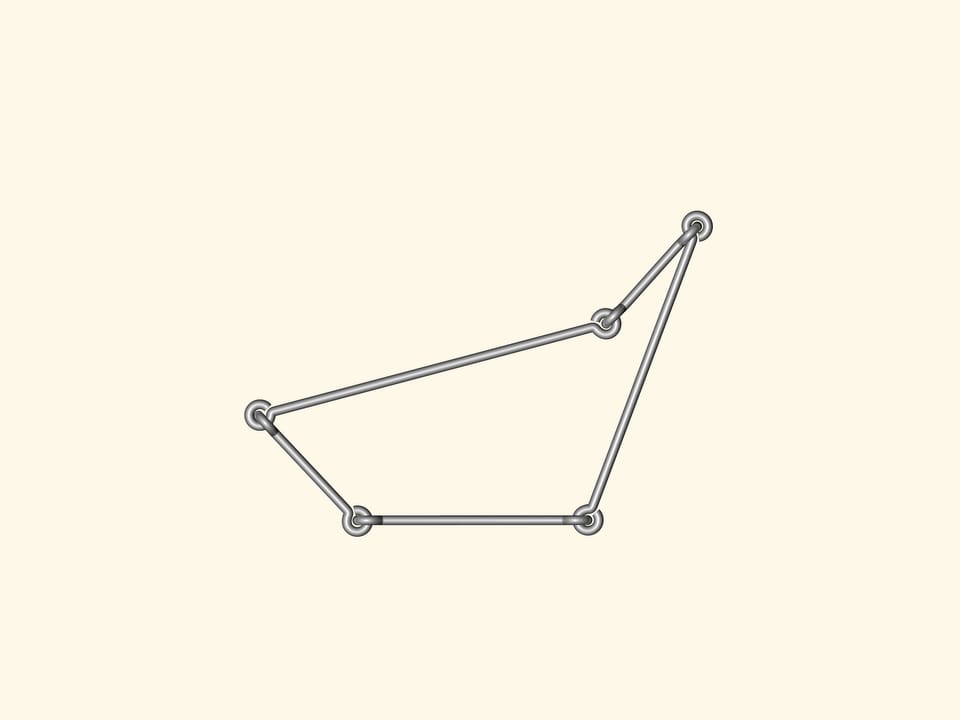
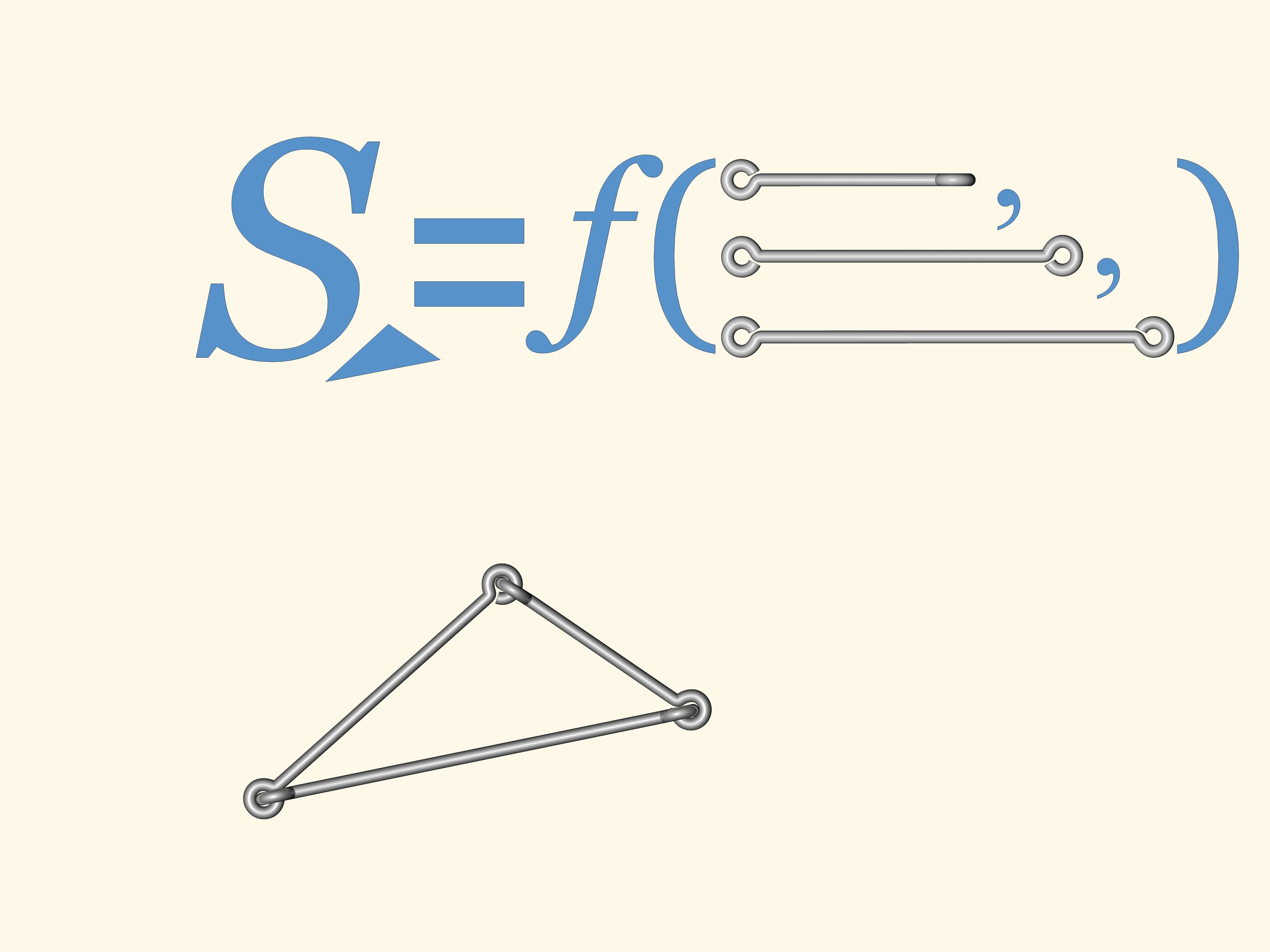
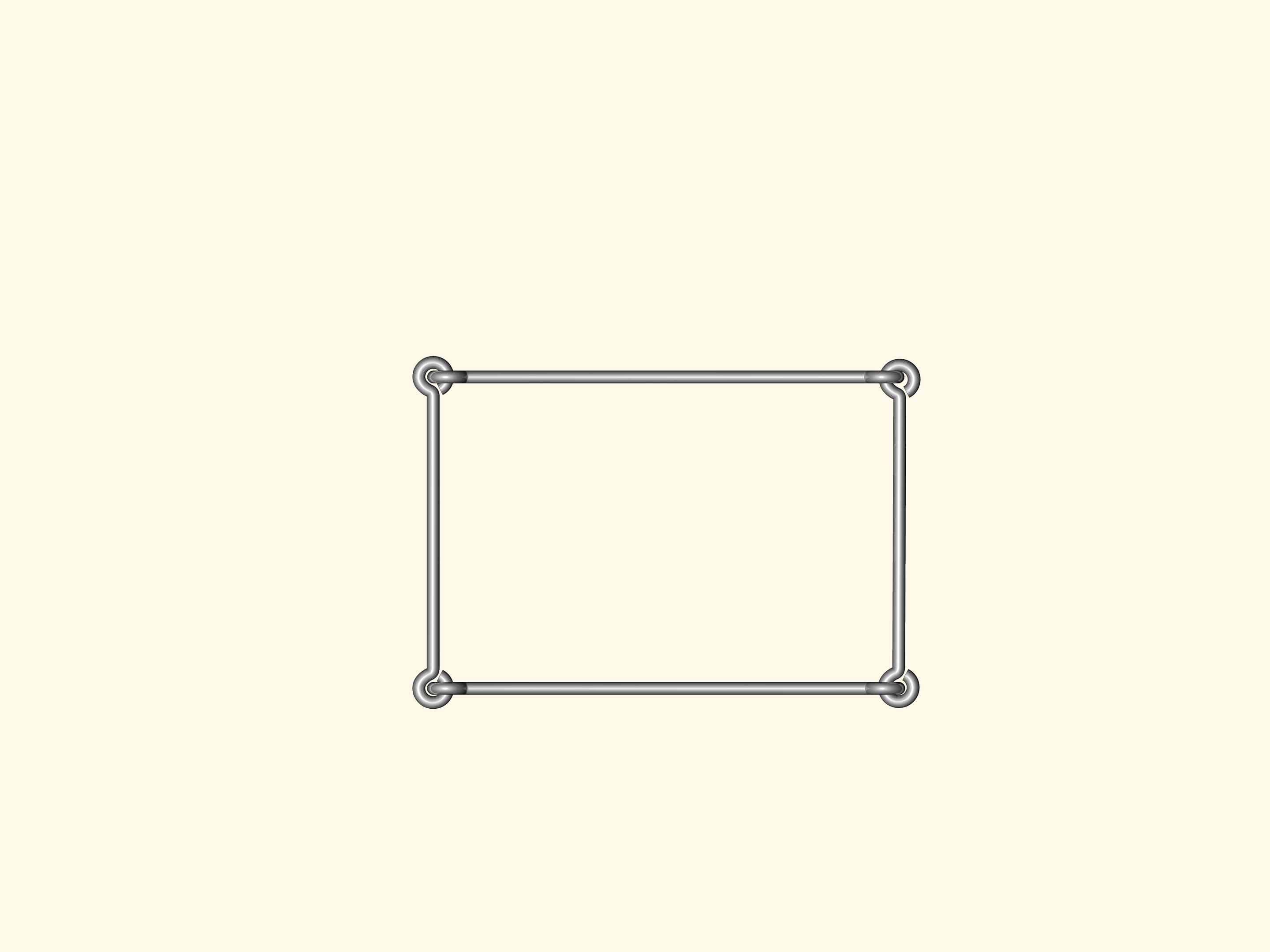
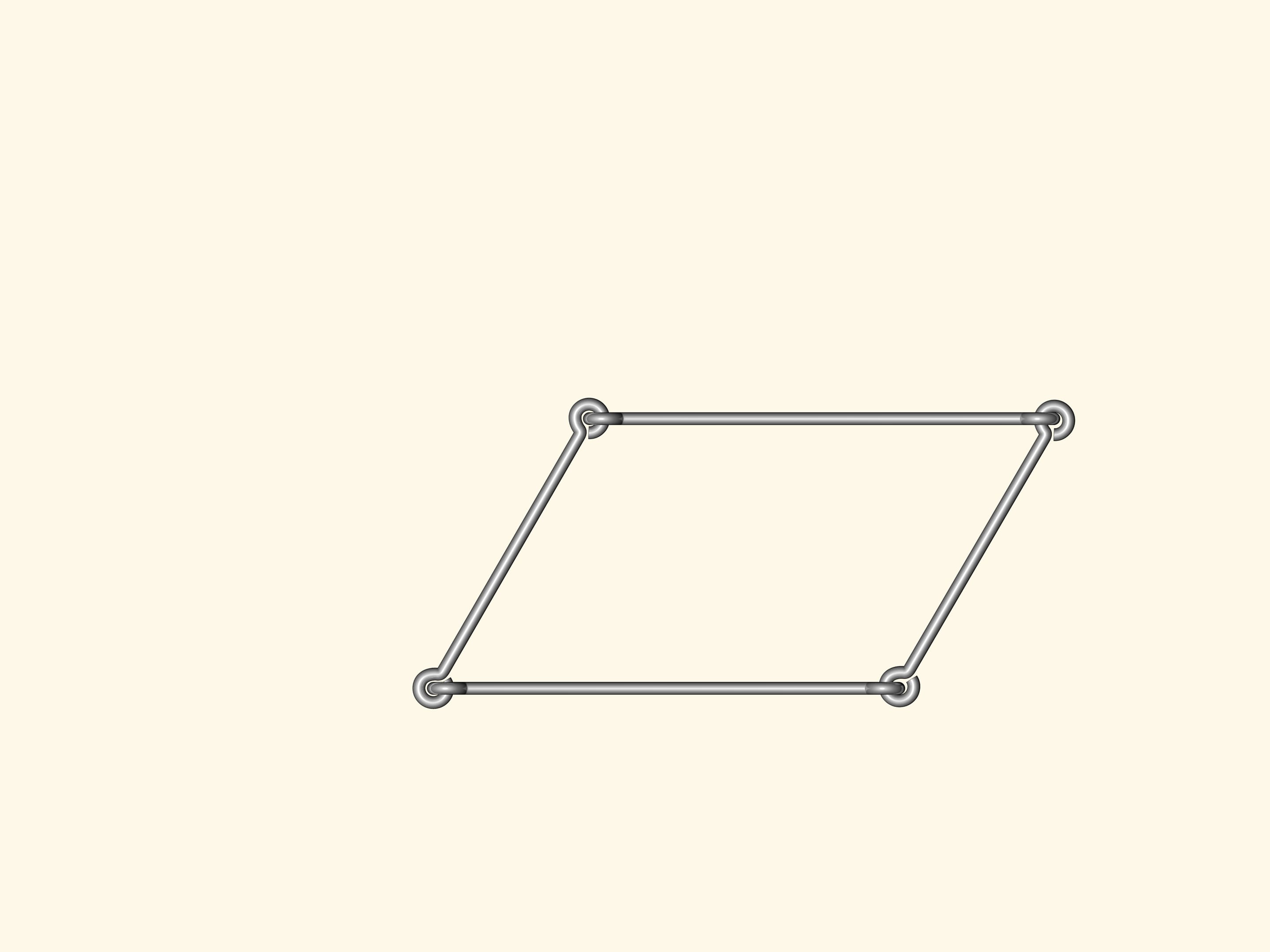
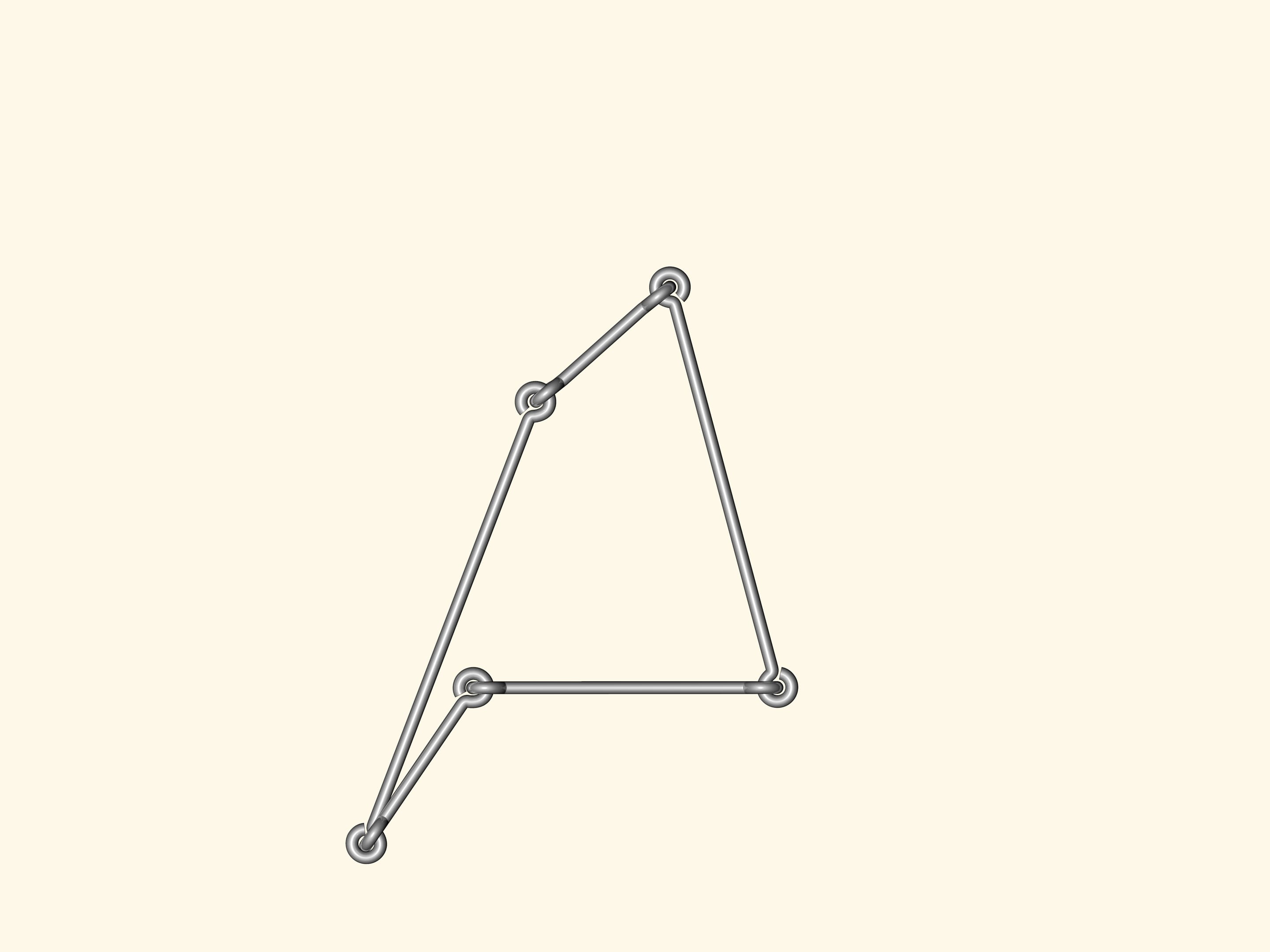
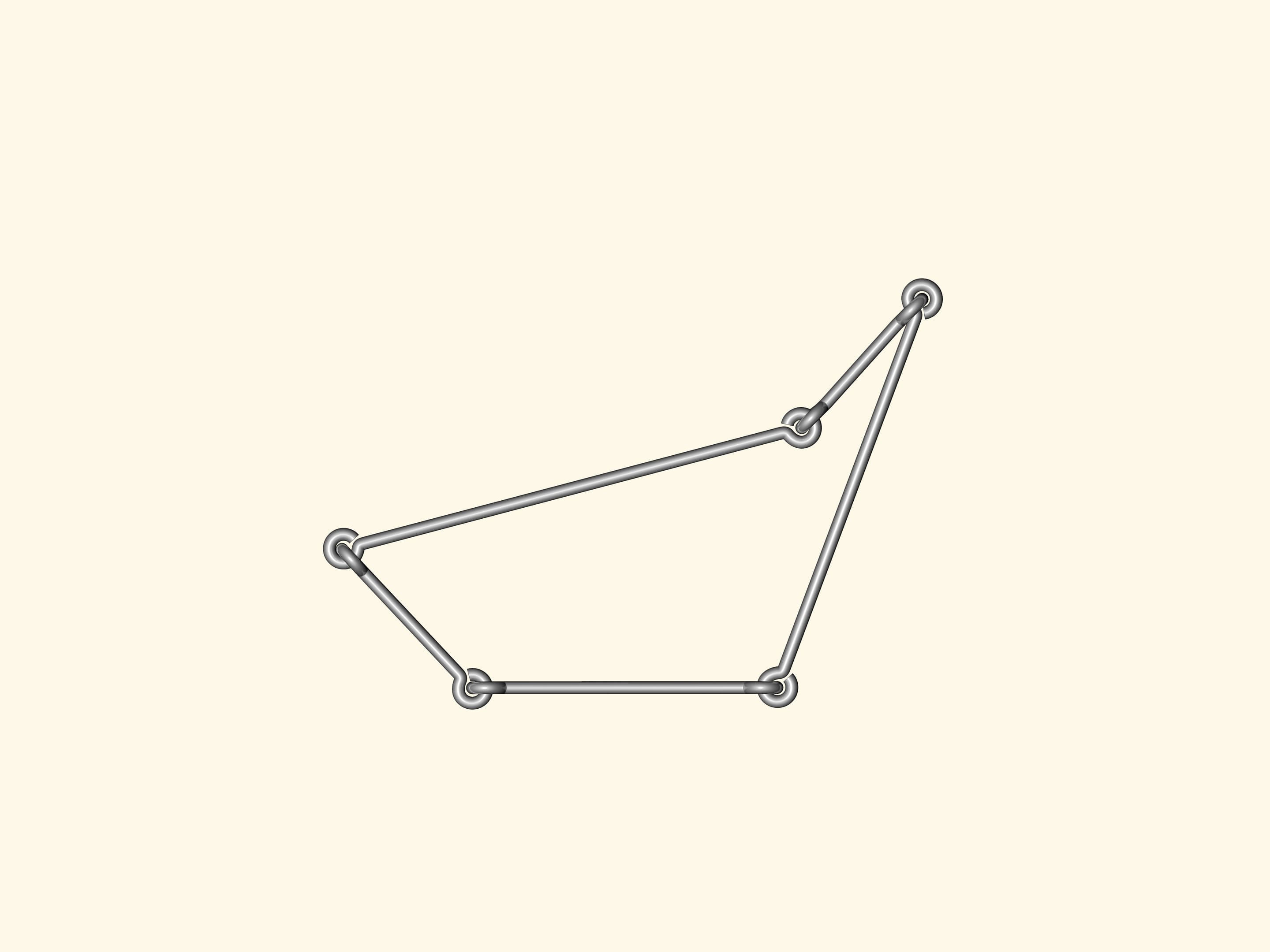
Y a–t–il des poly­gones flexibles? C’est–à–dire, des poly­gones avec les côtés de longueur fixe, mais avec les angles non fixes, de sorte que, en chan­geant les angles, les poly­gones peuvent changer de forme? Un modèle de ce type peut le faire tout le monde avec des côtés de fil de fer réunis de façon stan­dard.

Si nous construi­sons un poly­gone à quatre côtés ou plus, alors certai­ne­ment il va fléchir. En conséquence, l’analogue de la formule de Héron, qui calcule la surface du triangle à partir des longueurs des côtés seule­ment, ne peut exister pour un nombre de côtés supé­rieur à trois.

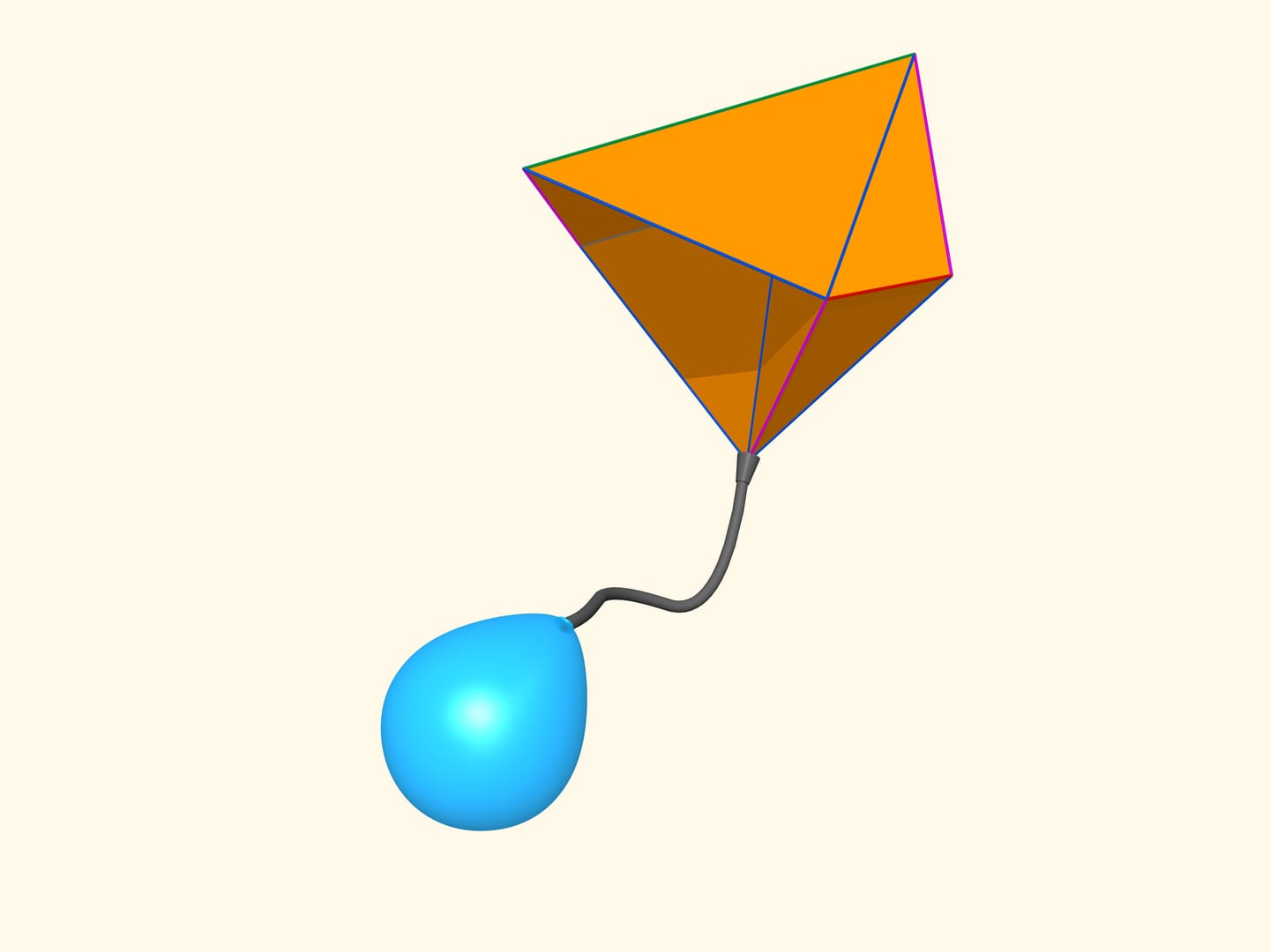
Reve­nons dans l’espace. Mais qu’est–ce que c’est un poly­èdre défor­mable, s’il existe? En analogie avec le problème dans le plan, ses côtés (avec dimen­sion infé­rieure d’une unité par rapport à la dimen­sion de l’espace) doivent être des faces poly­go­nales rigides. Les angles à deux dimen­sions, appelés dièdres, qui séparent deux faces, auront la possi­bi­lité de changer, et sont réalisés par des char­nières comme celle du piano à queue.

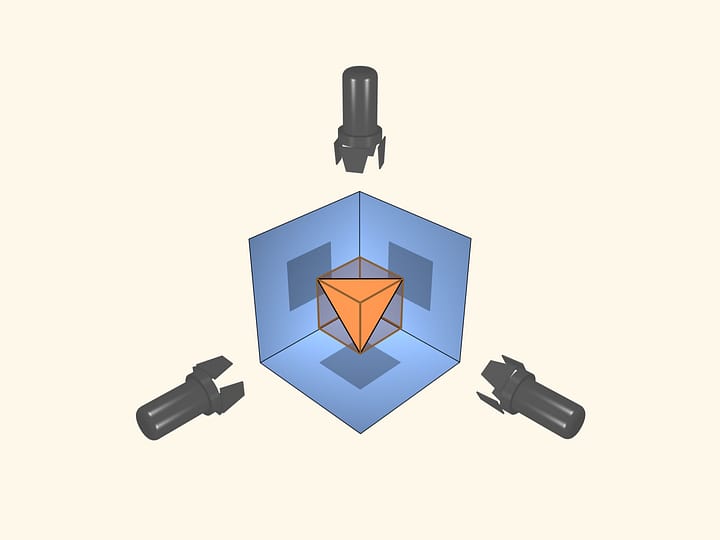
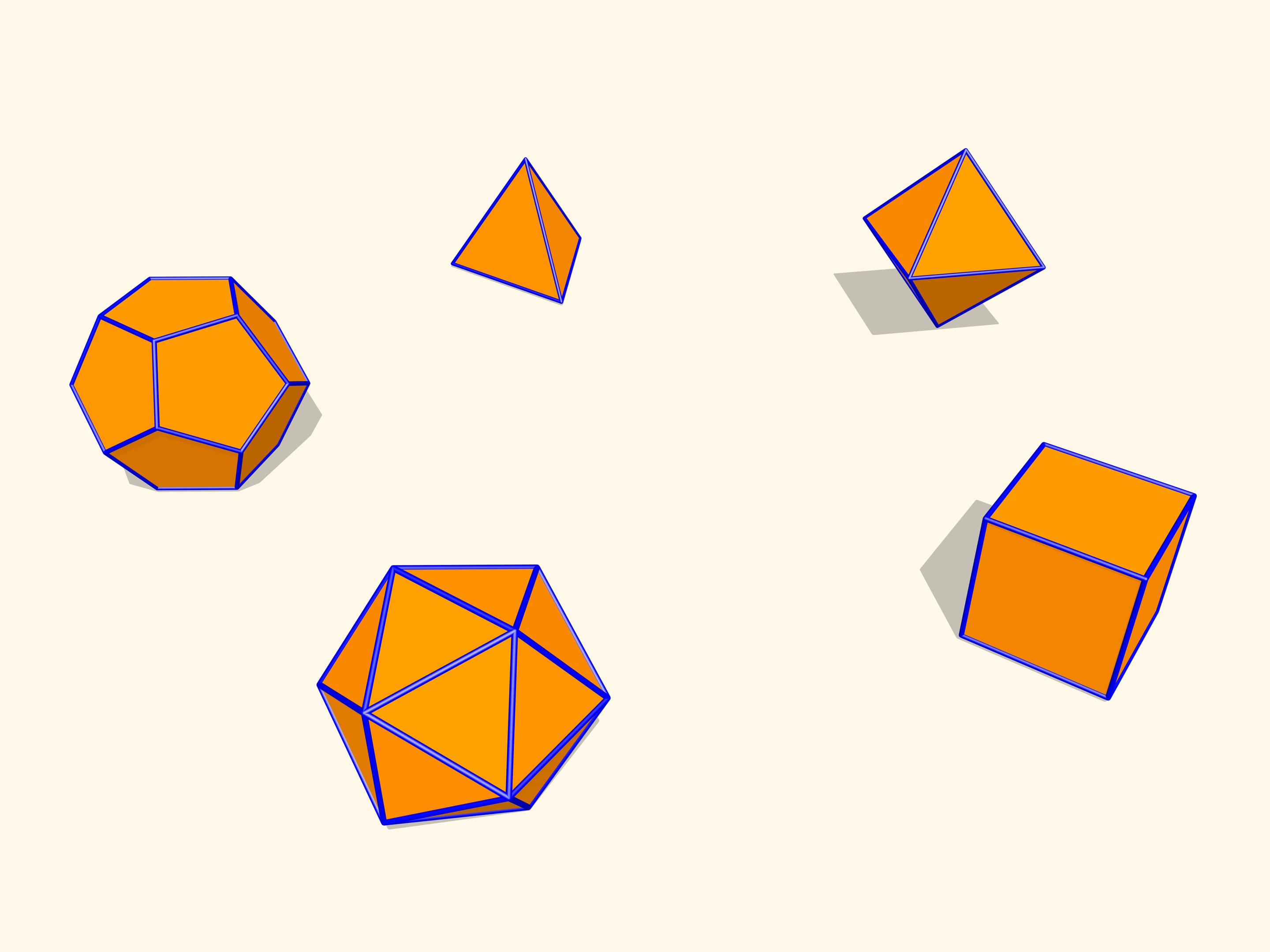
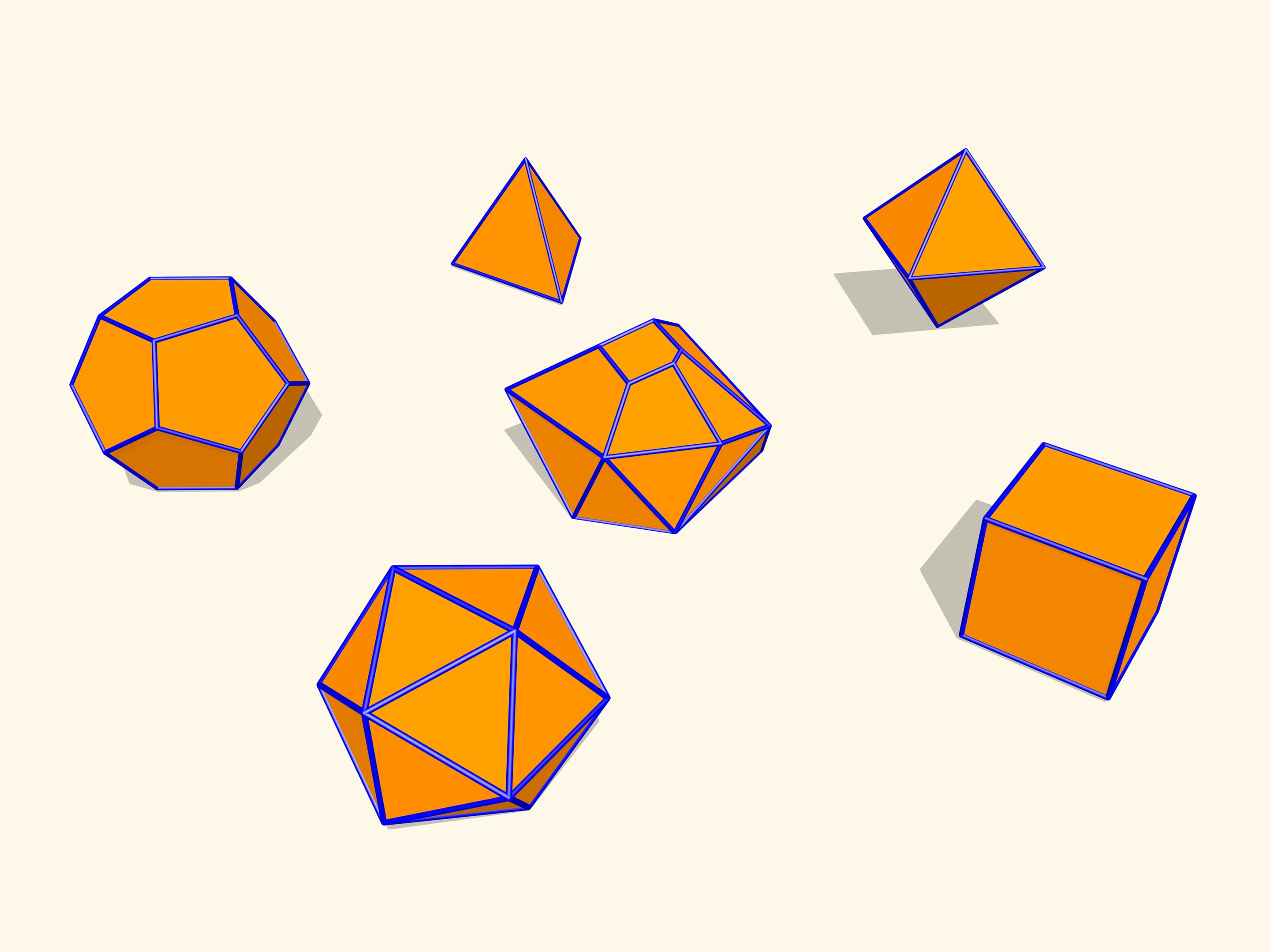
Pour commencer, obser­vons les poly­èdres régu­liers. Si nous en construi­sons des modèles avec des char­nières de piano le long de tous les arêtes, nous pouvons voir qu’il ne fléchissent pas. En fait, c’est une propriété de tous les poly­èdres convexes. Un théo­rème démontré par Auguste Louis Cauchy (1789—1857) en 1813 affirme que le poly­èdre convexe défini par un ensemble de faces avec les condi­tions de collage est unique. Autre­ment dit, un poly­èdre convexe flexible n’existe pas.

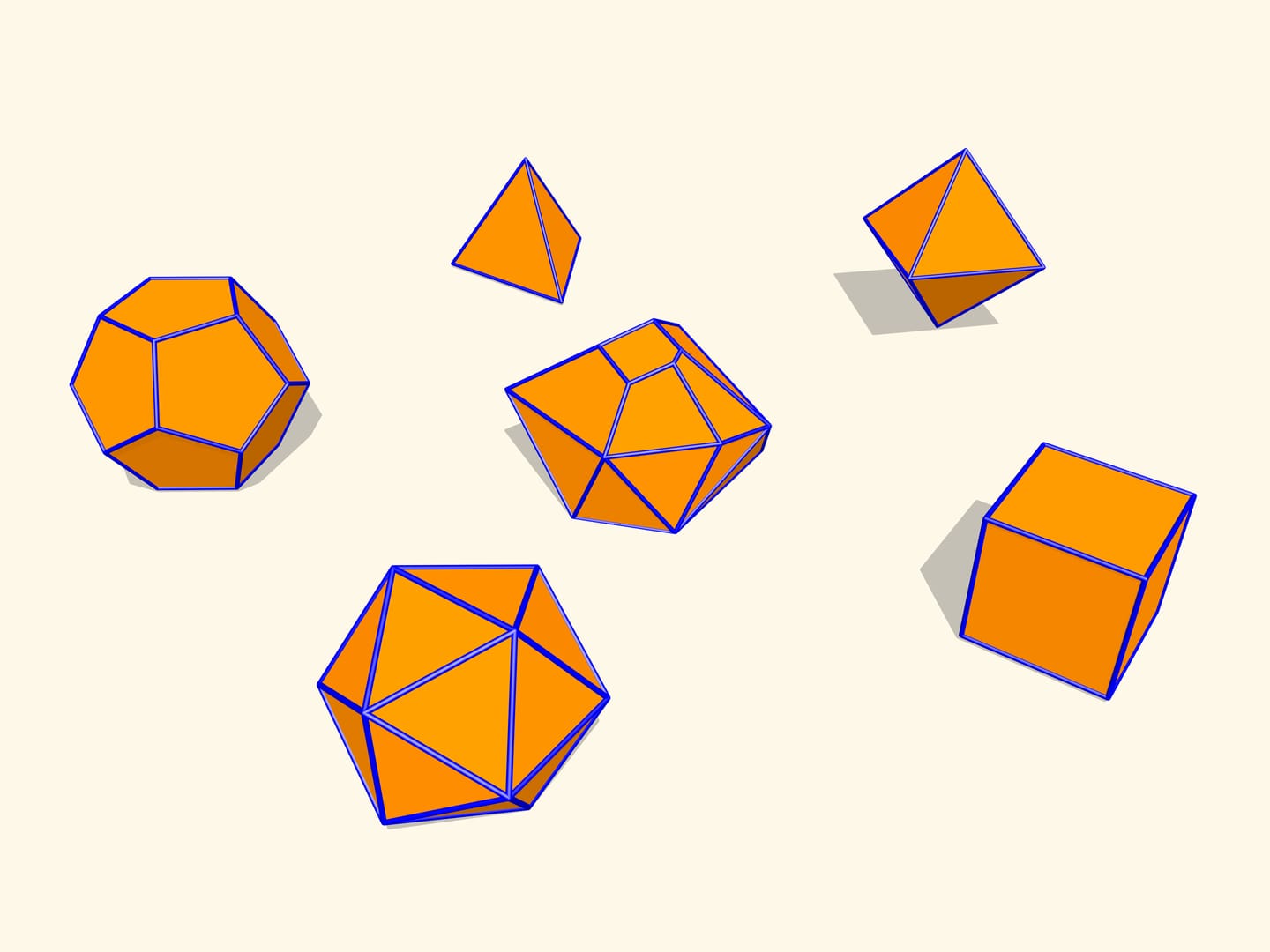
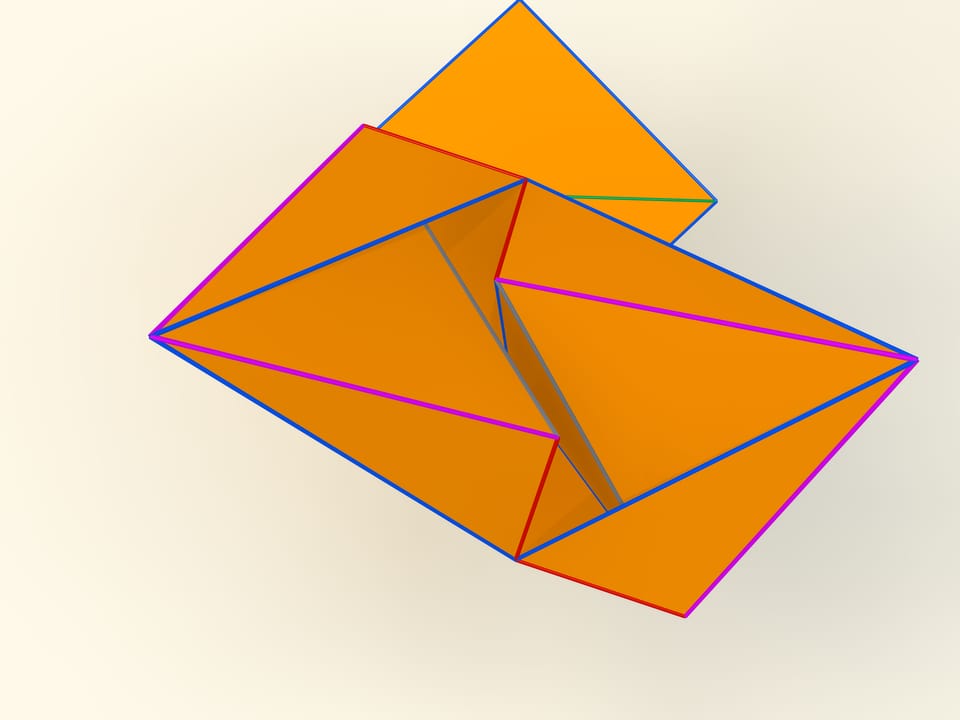
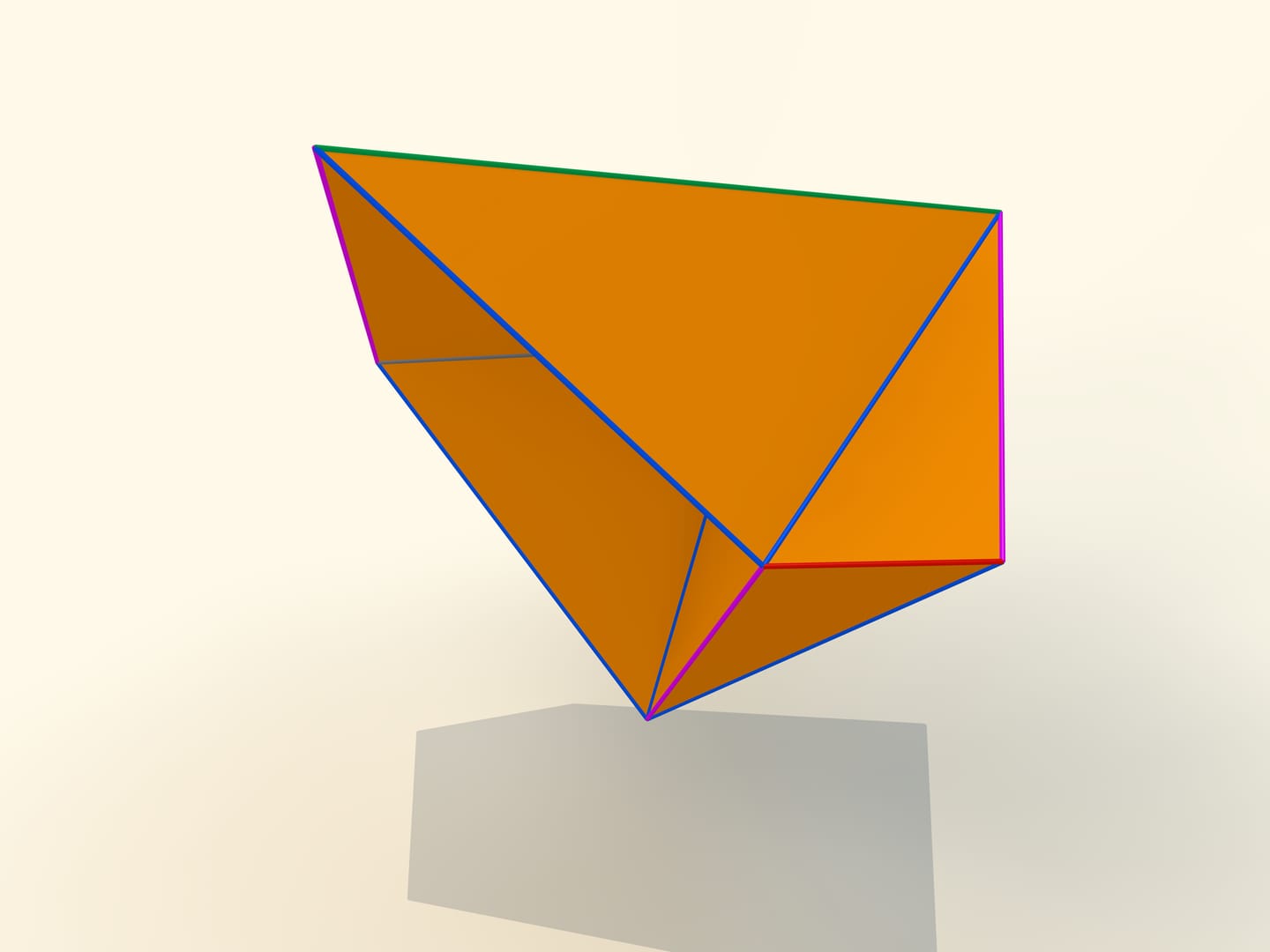
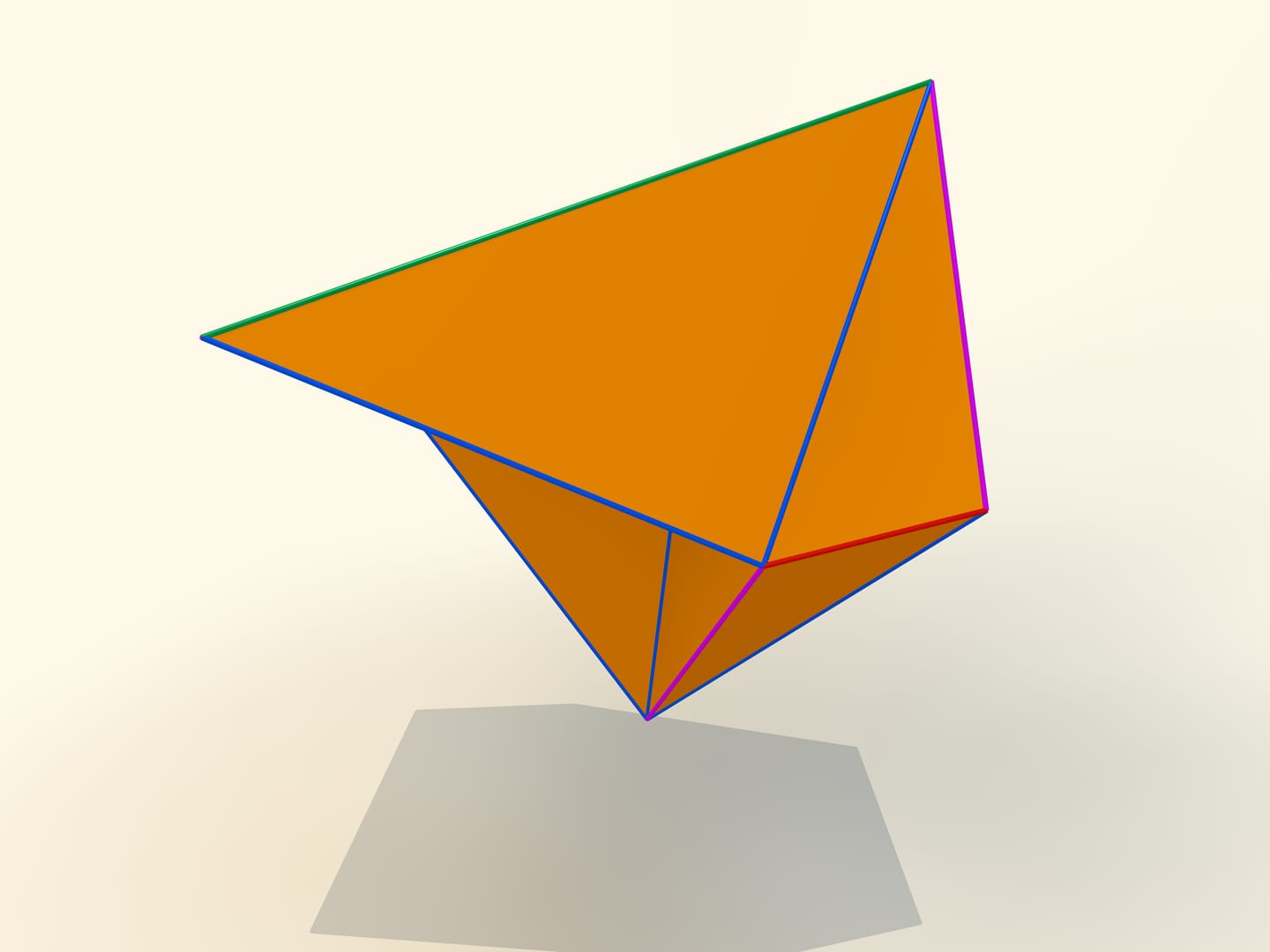
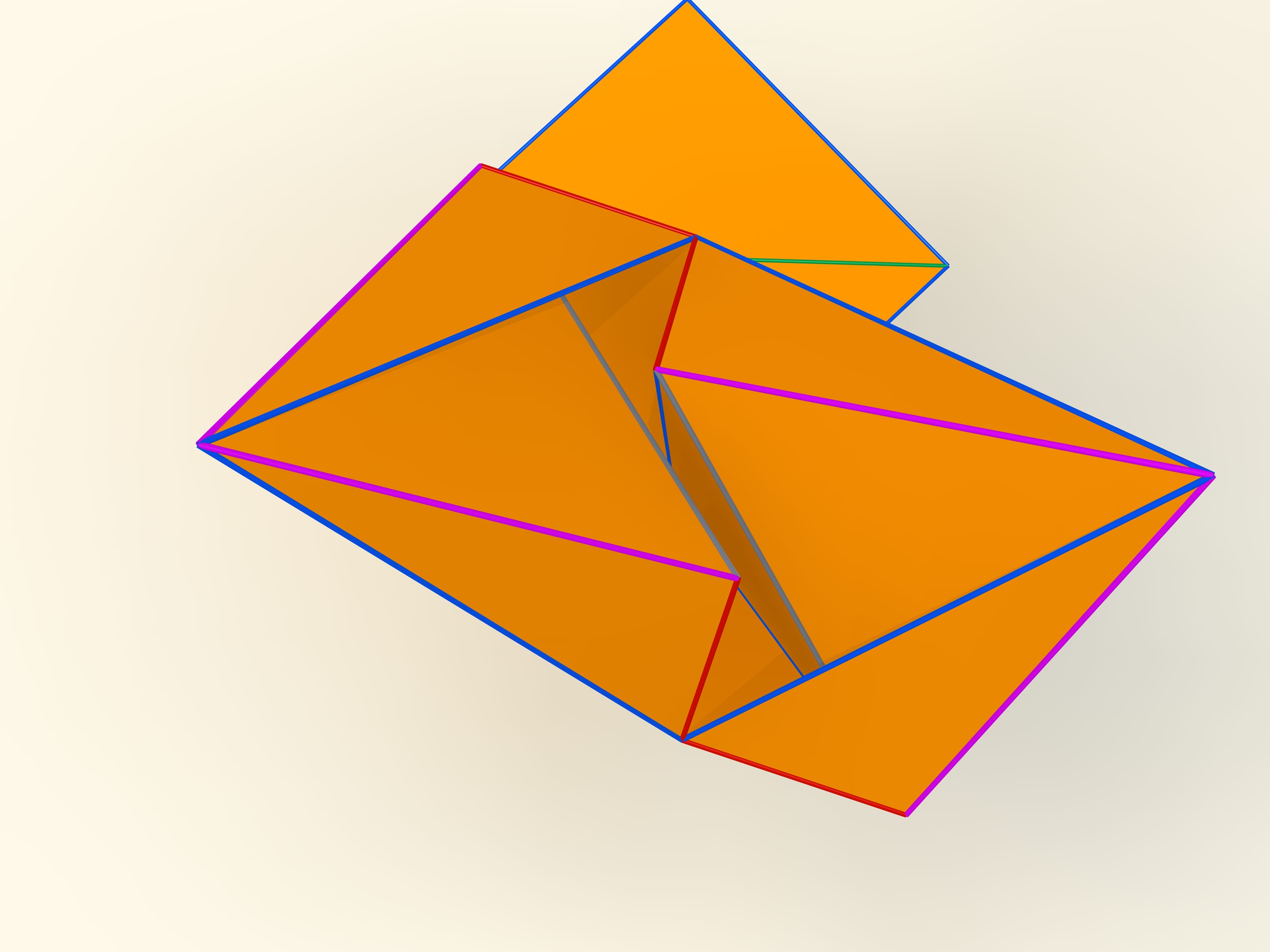
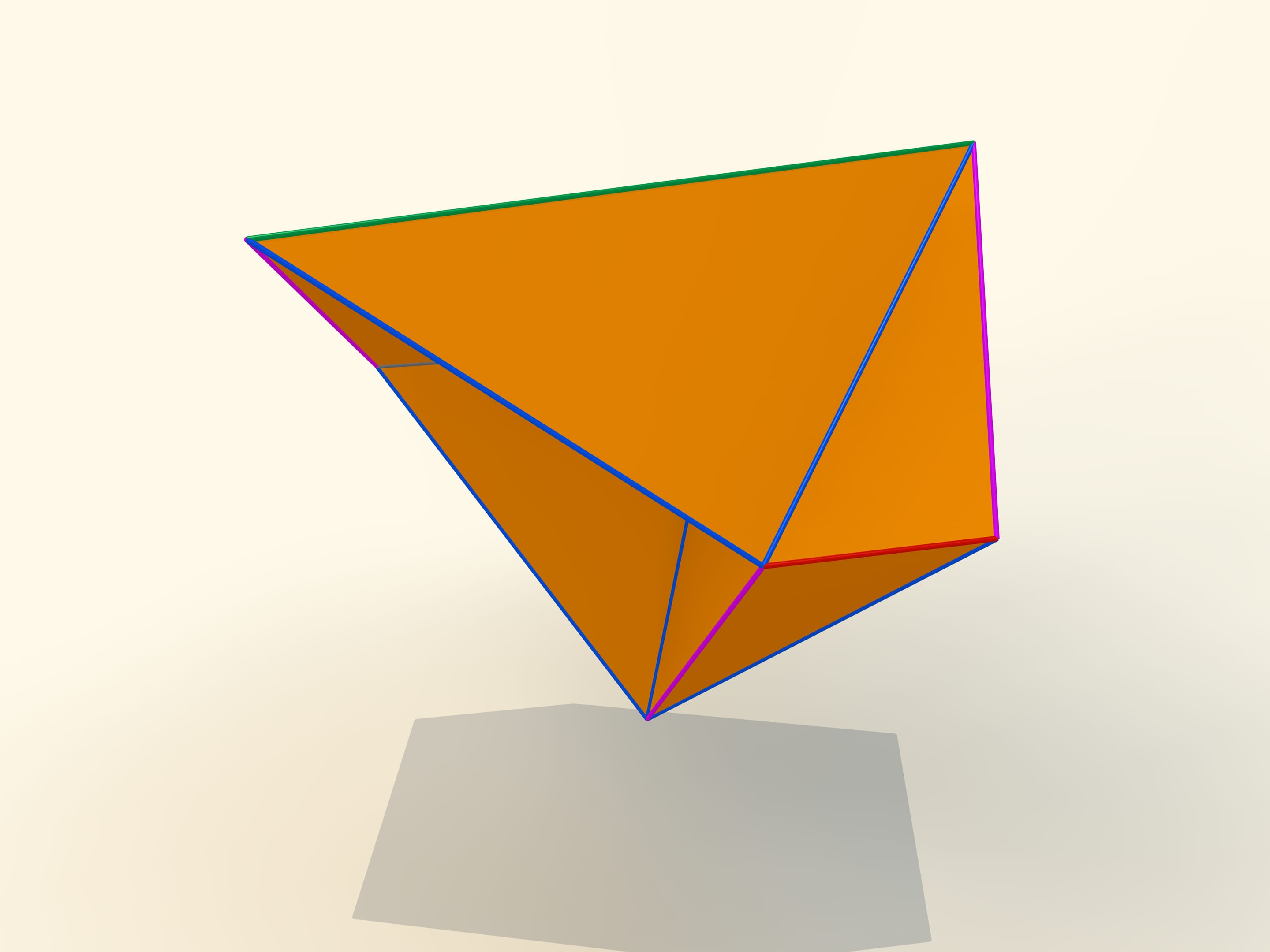
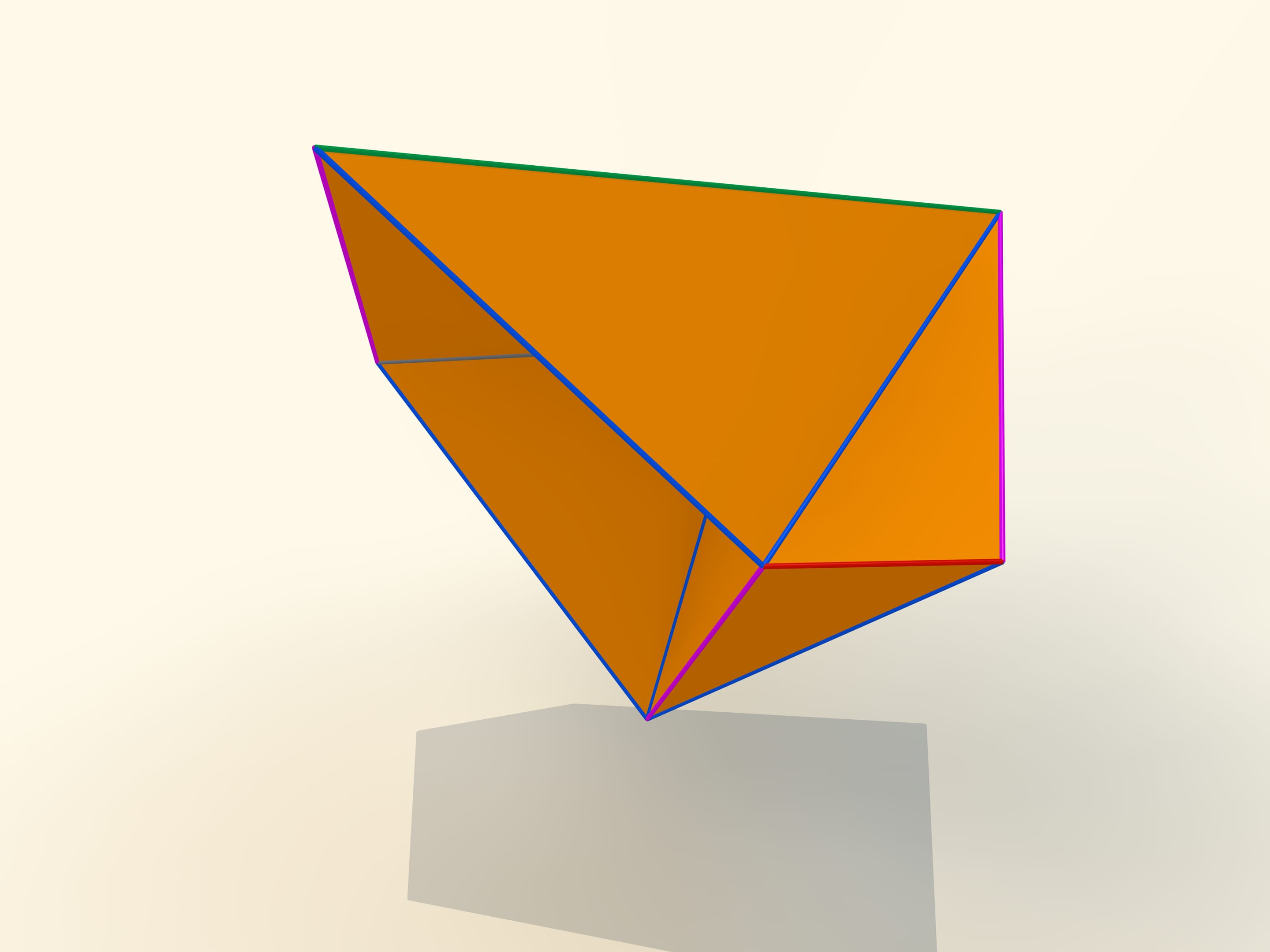
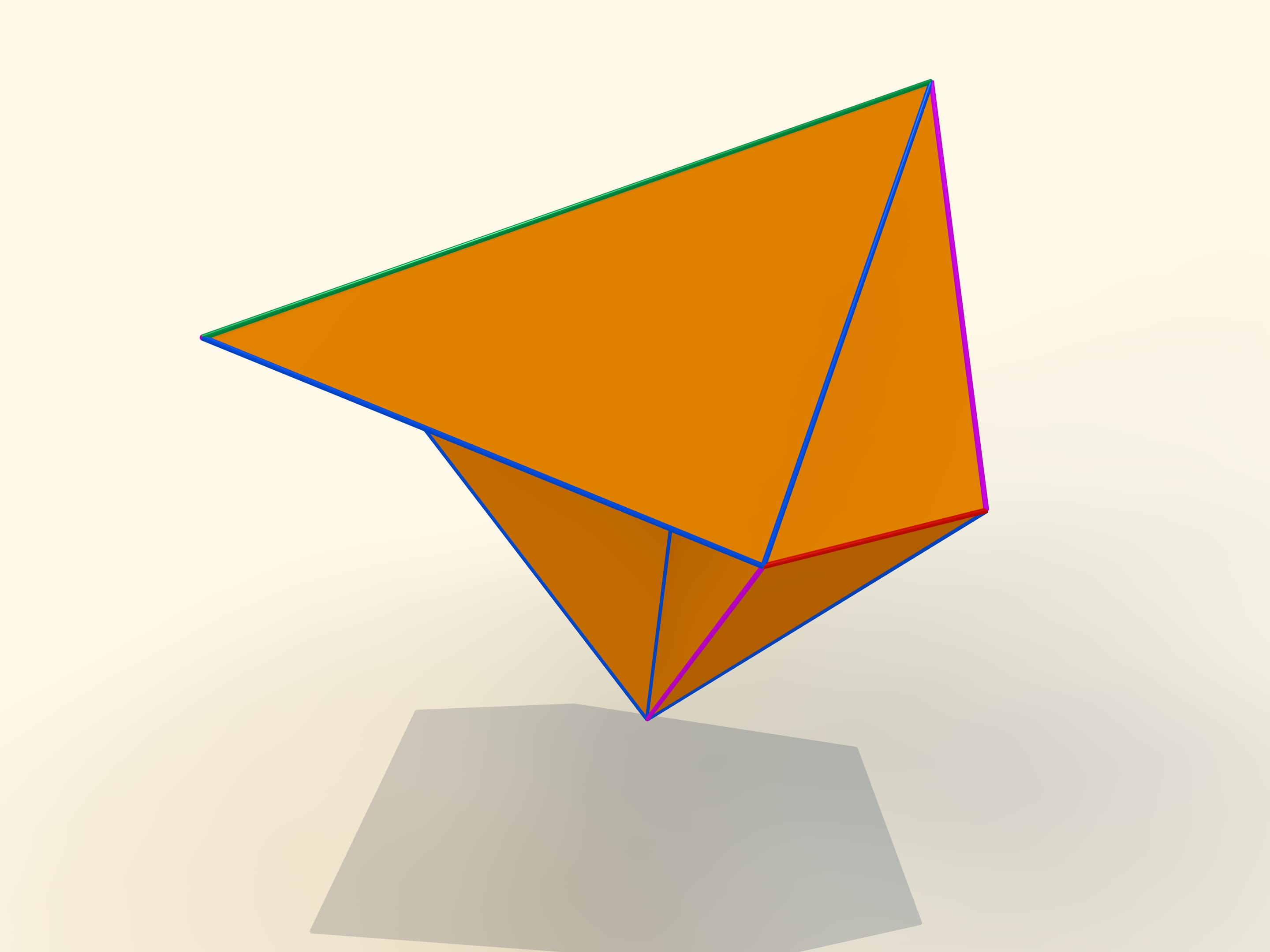
Les premiers exemples mathé­ma­tiques de poly­èdres défor­mables concernent, bien sûr, des poly­èdres non convexes. L’ingé­nieur belge P. Brikar en donna même une clas­si­fi­ca­tion en 1897. Nous avons dit «exemples mathé­ma­tiques», parce qu’ils sont non seule­ment des poly­èdres non convexes, mais ils ont aussi des auto–inter­sec­tions. Leurs faces se croisent les unes avec les autres. Du point de vue mathé­ma­tique, ils sont des poly­èdres, mais leur réali­sa­tion dans notre espace à trois dimen­sions est impos­sible. En 1975, le mathé­ma­ti­cien améri­cain P. Connelly a trouvé une façon d’éviter les auto–inter­sec­tions, et de «vrais» poly­èdres défor­mables sont apparus. Le plus simple d’entre eux qu’on connait aujourd’hui, a 9 sommets, 17 arêtes et 14 faces: on va le construire tout suite. Il a été inventé en 1978 par le mathé­ma­ti­cien alle­mand Klaus Steffen.

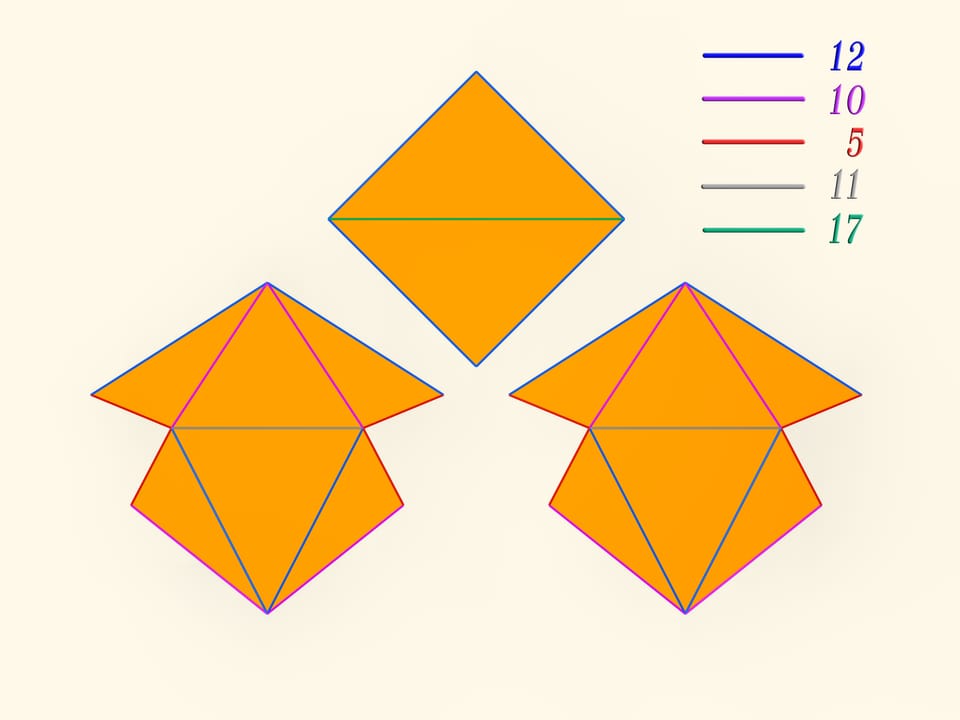
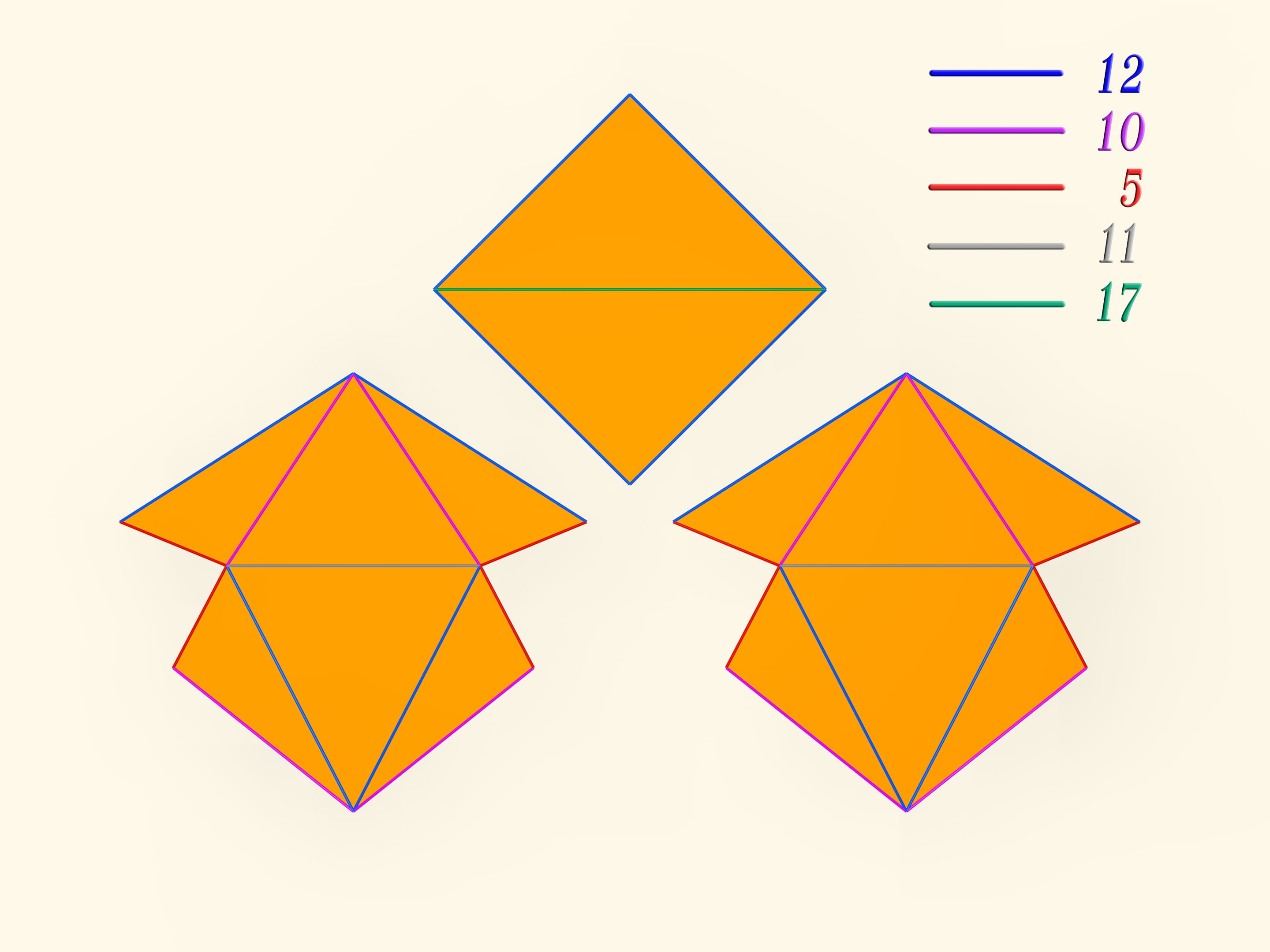
Le déve­lop­pe­ment du poly­èdre de Steffen se compose de deux parties iden­tiques plus un «toit». Même en rappe­lant la forme du déve­lop­pe­ment, mais ne sachant pas la longueur des bords, c’est extrê­me­ment diffi­cile construire un tel poly­èdre: la possi­bi­lité de défor­ma­tion est une excep­tion pour les poly­èdres, et en fait très peu entre eux la possèdent.

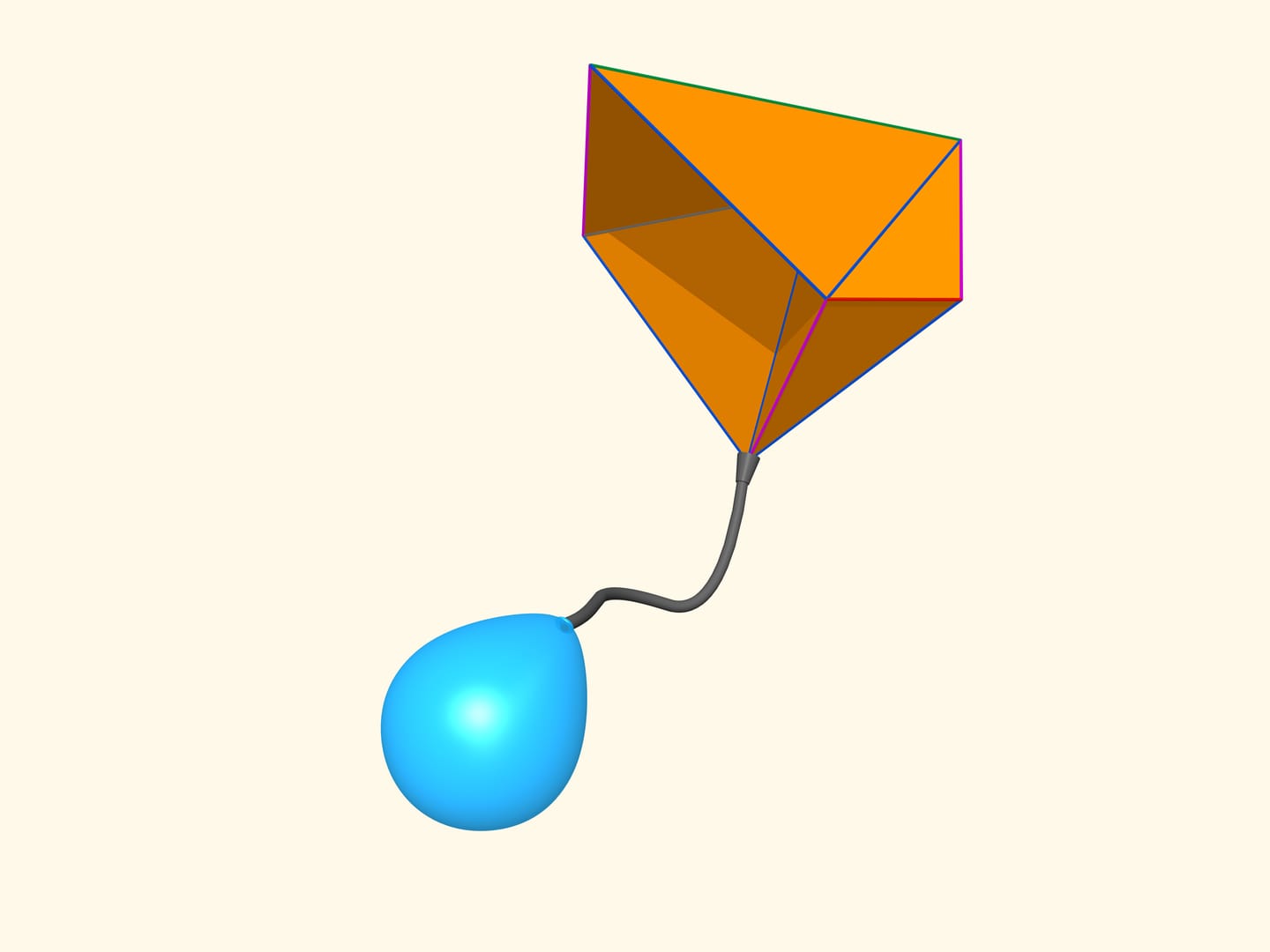
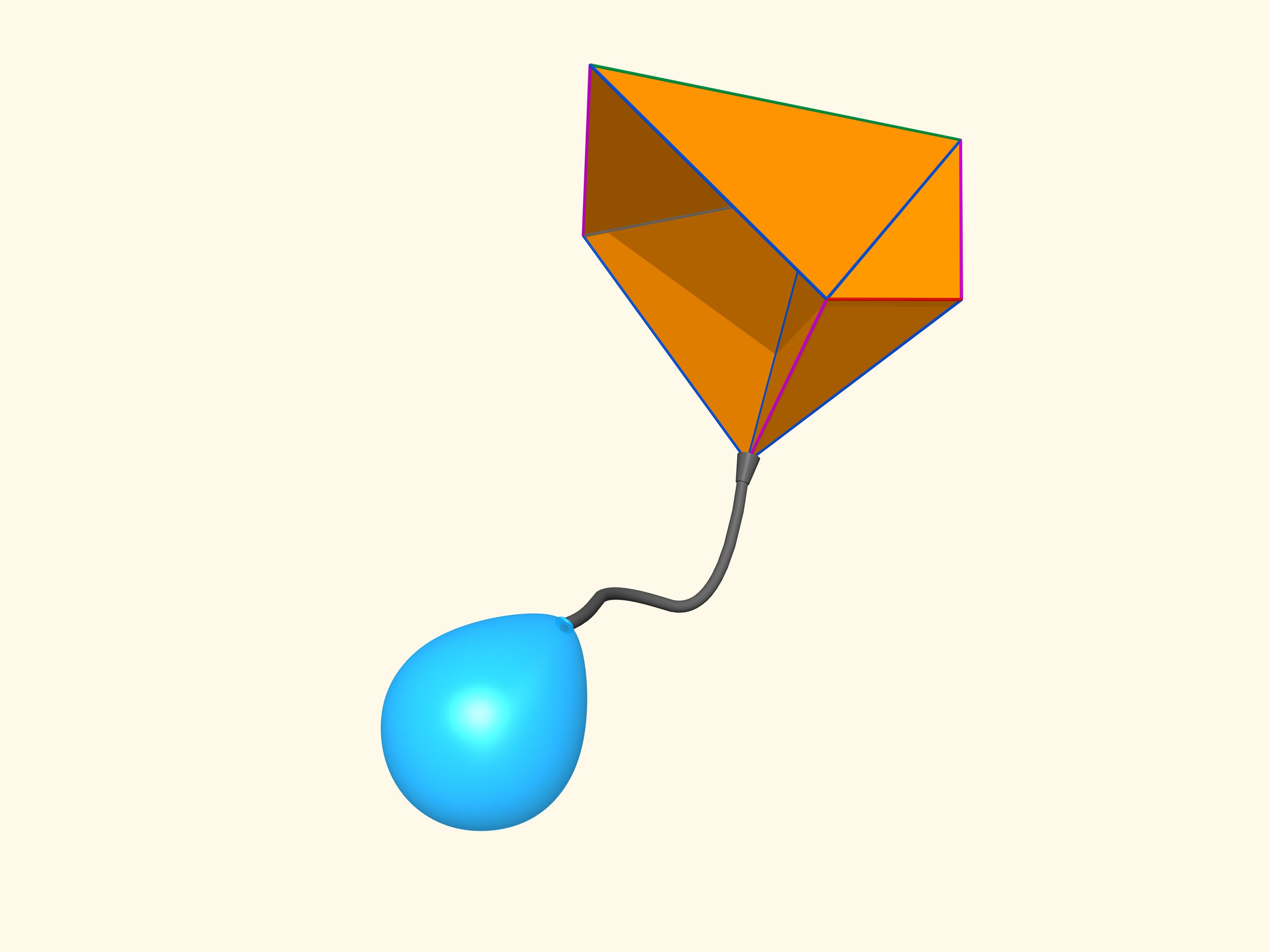
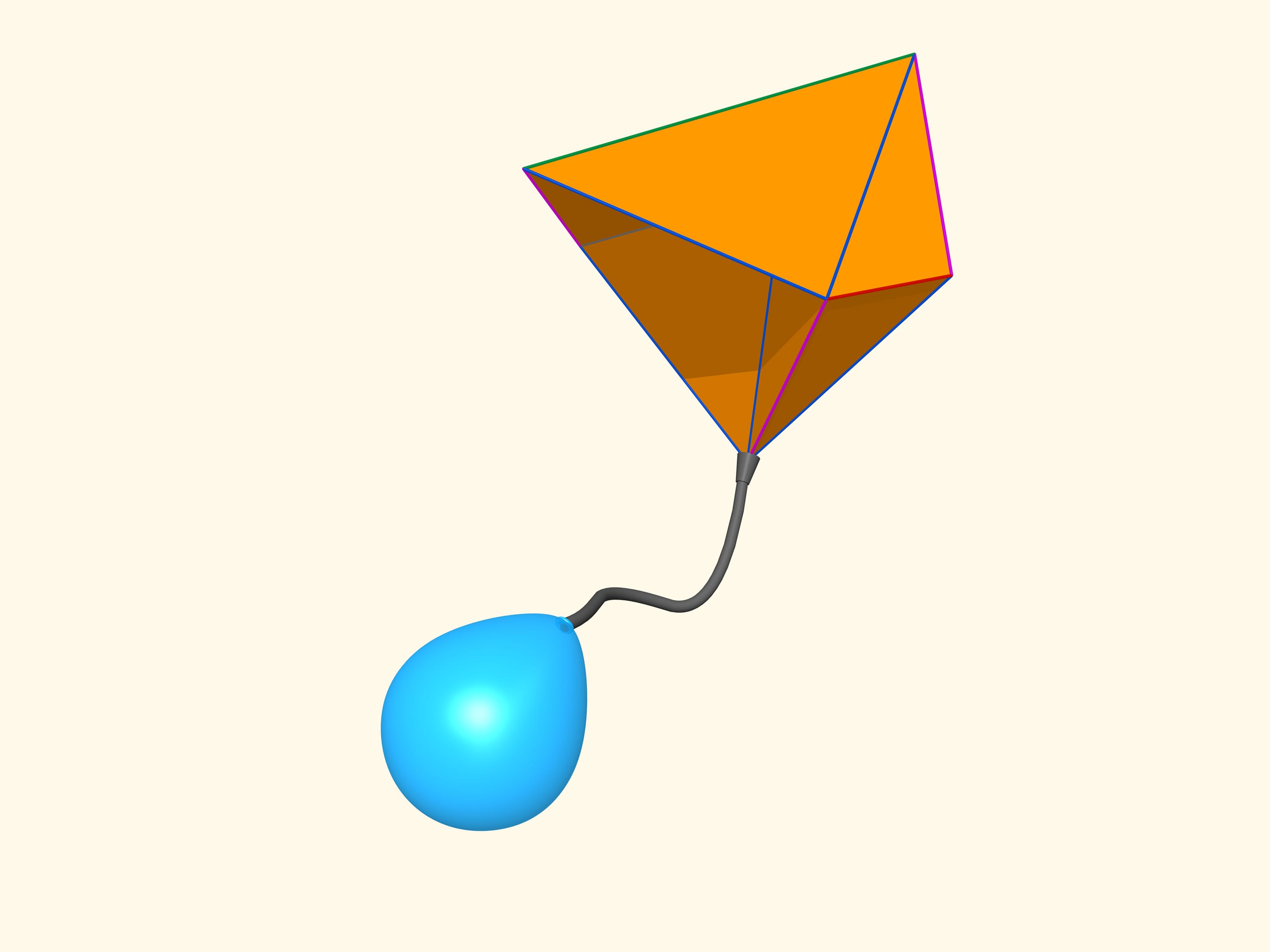
Lorsque les mathé­ma­ti­ciens ont réalisé qu’il y a des poly­èdres défor­mables, une ques­tion s’est posée, ce qui devint connu comme «la conjec­ture du souf­flet». Comment le souf­flet se gonfle? Comment fonc­tionne l’accor­déon? Leur prin­cipe de fonc­tion­ne­ment est le chan­ge­ment de volume inté­rieur. Et qu’advient–il des poly­èdres défor­mables? Vont–ils changer leur volume par la défor­ma­tion? Est–ce qu’on peux construire un souf­flet, ou bien un accor­déon, en n’utili­sant pas de la peau, mais du maté­riau rigide, sous la forme de poly­èdre?

A la fin du XXe siècle, une réponse complète à cette ques­tion a été trouvé par le mathé­ma­ti­cien russe I.H. Sabitov. Il arrive que, pour les volumes des poly­èdres, y compris ceux qui sont défor­mables, il existe un analogue de la formule de Héron pour l’aire du triangle. Plus préci­sé­ment, il existe un poly­nôme en une variable, tel que ses coef­fi­cients ne dépendent que des longueurs des arêtes du poly­èdre, alors que le volume est une racine de ce poly­nôme. Mais le nombre des racines réelles d’un poly­nôme d’une variable sont des nombres concrets, placés à une certaine distance entre eux. Pour de petites défor­ma­tions du poly­èdre, le volume devrait changer légè­re­ment, et, par conséquence, il ne peut pas sauter d’une racine à l’autre. Cela signifie que le volume des poly­èdres défor­mables ne change pas avec leurs défor­ma­tions!

Nous avons examiné la ques­tion des poly­èdres défor­mables dans le plan (poly­gones) et dans notre espace tridi­men­sionnel. Mais qu’est–ce qui se passe dans les dimen­sions supé­rieures? Là aussi il existe des poly­èdres défor­mables, bien que beau­coup moins. Mais le problème du chan­ge­ments ou non dans le volume des poly­èdres défor­mables de dimen­sion plus grande que trois n’a pas encore été résolu, et attend son cher­cheur.