Après la guerre, en 1947, on introduisit dans l’Union soviétique de nouveaux billets, qui étaient encore en circulation en 1956.
En cette année, Vladimir Igorevich Arnold posa le problème du rouble plié. Est–ce qu’on peut construire un polygone planaire en pliant une feuille de papier (un billet de un rouble) afin que le périmètre de ce polygone est plus grande que le périmètre de la feuille de depart?
En 1961 en Russie on changea à nouveau les pièces et les billets de banque, de sorte que aussi le billet d’un rouble a changé, en devenant une feuille de papier beaucoup plus petite. A cette époque, cependant, le problème n’était encore résolu.
Par ailleurs, même si la réponse positive «c’est possible» est en contradiction avec l’intuition, il doit y avoir une raison mathématique pour la réponse négative. Si l’on plie un rectangle le long d’une ligne droite, son périmètre ne peut qu’en résulter réduit: au bord déjà existant il faut ajouter le segment de droite le long de laquelle on a pris le pli, mais il faut supprimer une ligne brisée qui a les mêmes extrêmes de ce segment. Si maintenant on fait une chose pareille, c’est–à–dire on plie le polygone obtenu le long d’une ligne droite, la situation est la même: le périmètre augmente de la longueur d’un segment, mais diminue de la longueur d’une ligne brisée. Ce type de pliage — le long d’une ligne droite — est appelé «simple» et ne peut jamais diminuer le périmètre. Ce n’est cependant qu’une raison, mais pas encore une preuve.
Mais alors, peut–on ou non augmenter le périmètre du rectangle initial? Dans les années 1991 et 1993, les billet de banque ont été changés encore, et le billet d’un rouble du ’61 est sorti de la circulation. Mais le problème d’Arnold restait non résolu.
Depuis ce temps, un rouble russe vaut, malheureusement, si peu qu’il n’y a plus de billet d’un rouble, mais seulement des pièces de cette valeur.
Au début de l’XXIe siècle, toutefois, le problème a été résolu. La première solution mathématique rigoureuse a été donné par un élève de N.P. Dolbilin, Alexei Tarasov. Il a inventé un algorithme pour le pliage d’un carré de sorte qu’au total on obtient un polygone planaire avec un périmètre plus grande.
Ceux qui ne souhaitent que de profiter du film, peuvent sauter la prochaine partie, qui est ajouté pour ceux qui veulent bien comprendre la façon de plier le carré.
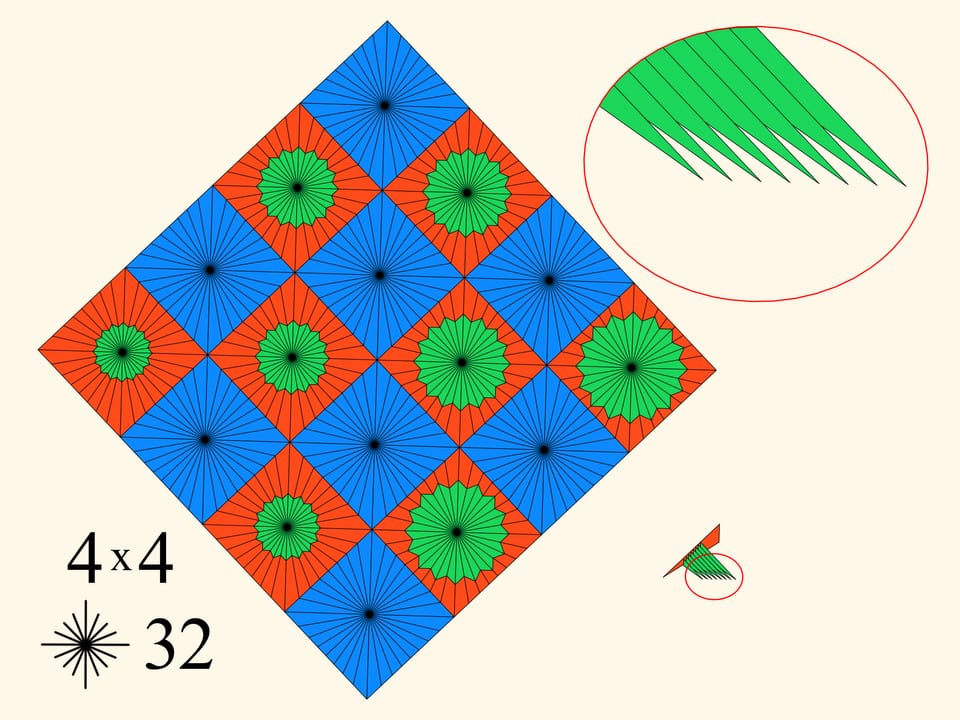
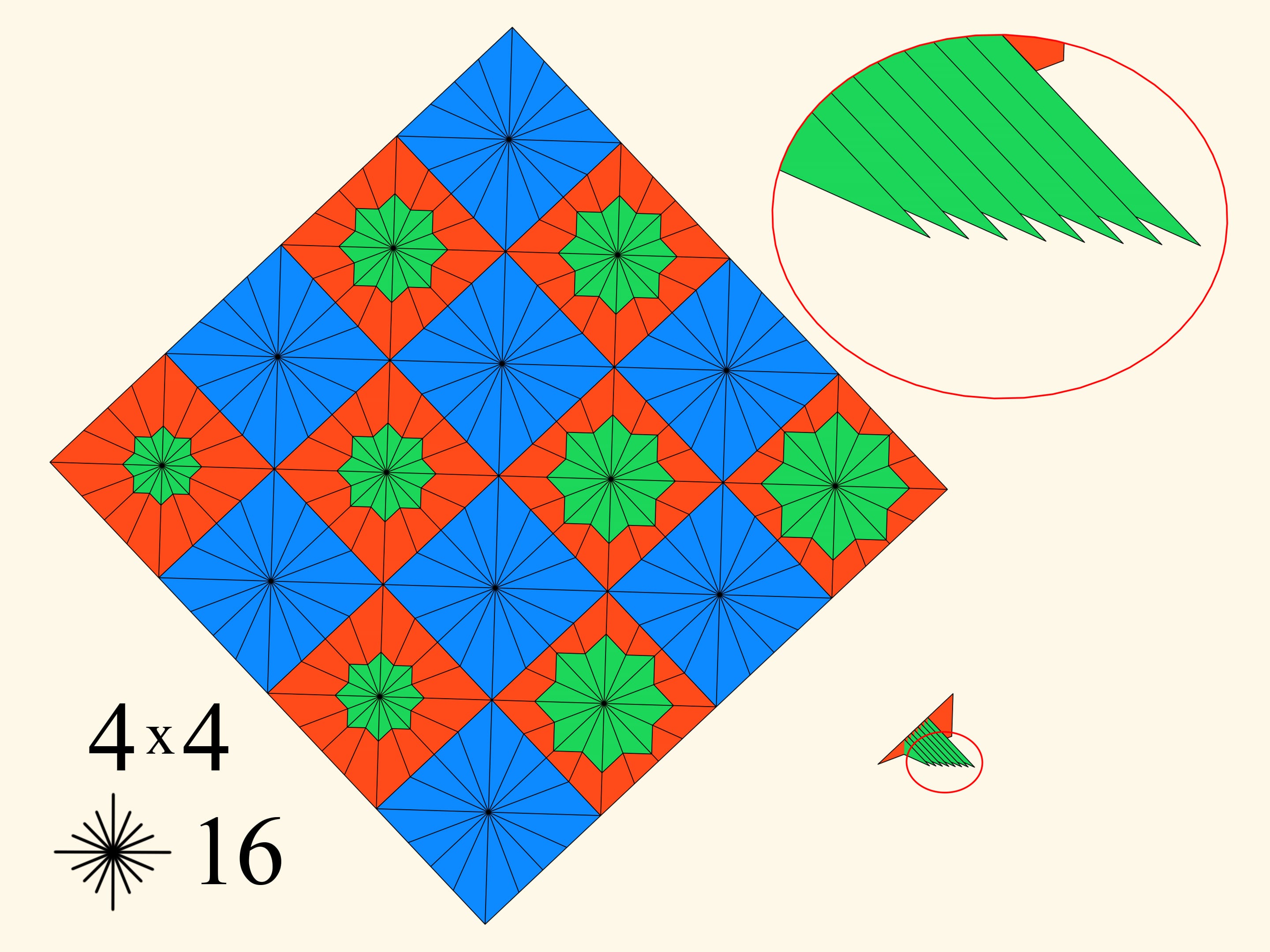
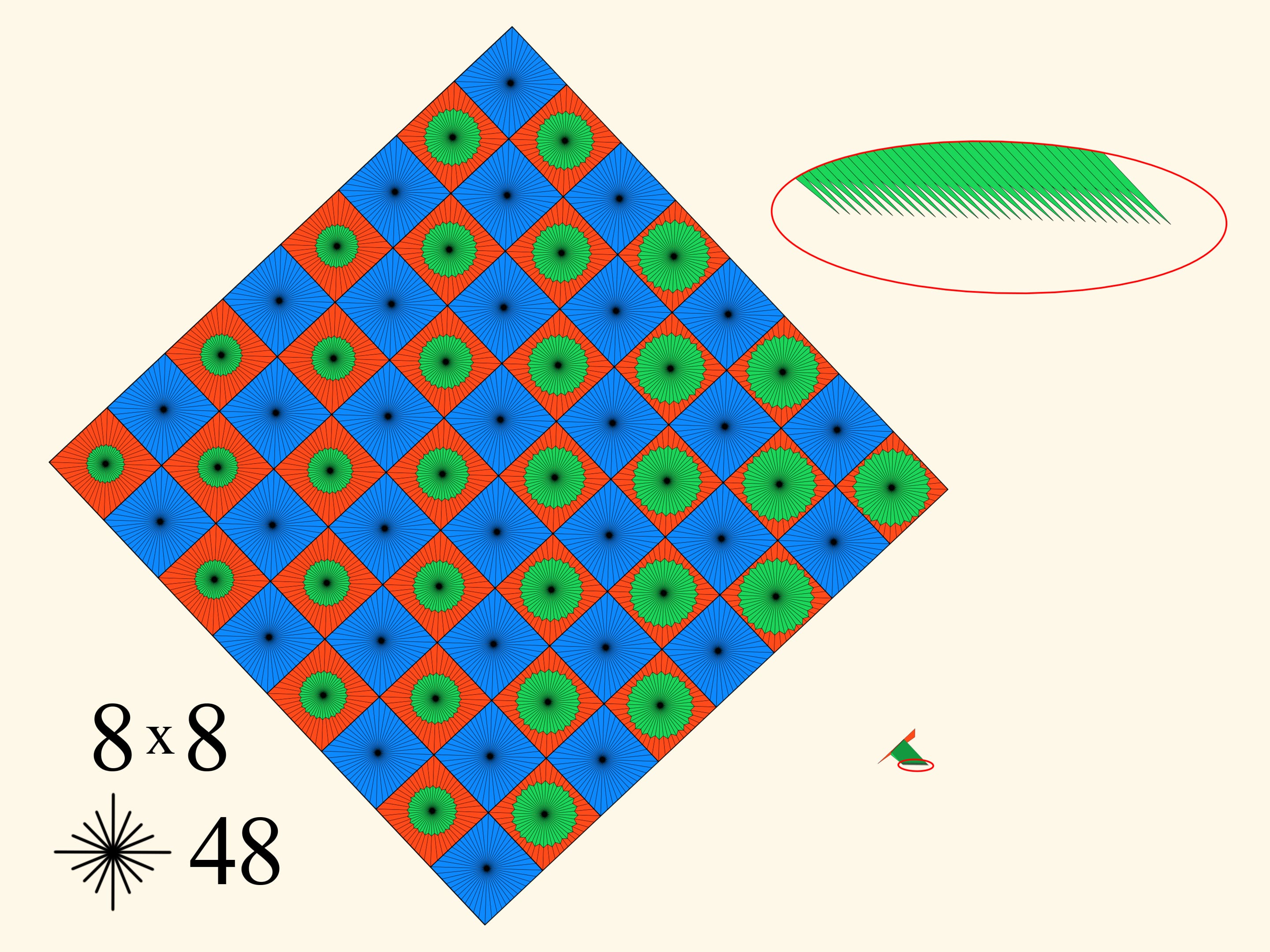
Prenons une feuille de papier carrée. Nous allons la diviser en cases carrées, par exemple, 4x4. Les cases seront coloriées par deux couleurs, comme un damier, et du centre de chaque carré on tirera un nombre défini de rayons. Après on ajoutera dans chaque case rouges une étoile verte, de sorte que la taille de ces étoiles ira croître dans la direction d’une diagonale. Maintenant nous plions le papier en une bande, puis en un rectangle, et, finalement, en un triangle. L’objet résultant est fait comme il suit. Il contient dans une moitié plusieurs couches bleu, et dans l’autre moitié plusieurs couches rouges et vertes. Le pliage a été faite de telle façon que les étoiles vertes, après le pliage, augmentent en taille quand on passe d’une couche à une autre, comme si elles étaient l’une dans l’autre. Commençons donc à plier le triangle dans chaque couche de sorte que les couches bleus sortent parallèles d’un côté, et les couches vertes et rouges sortent de l’autre côté. Nous obtenons une surface qui finit par être repliée à nouveau dans un polygone planaire.
Ce polygone a une partie rouge (les triangles bleus restent cachés en dedans) et un peigne vert. Nous observons que le peigne a un nombre de dents égal au nombre d’étoiles vertes, c’est à dire de carrés rouges.
Mais le périmètre est–il augmenté par rapport à celui du carré initial? Est–ce que le problème a été résolu? Si on compare les figures, on voit immédiatement que le périmètre est diminué. Pourquoi alors nous avons fait ce pliage si compliqué?
Dans cet exemple concret, nous avons utilisé un algorithme général. Et dans cet algorithme, il y a deux paramètres: le nombre de cases qui composent le carré initial et le nombre de rayons dans chaque carré. Regardons ce qui arrive si nous modifions ces paramètres.
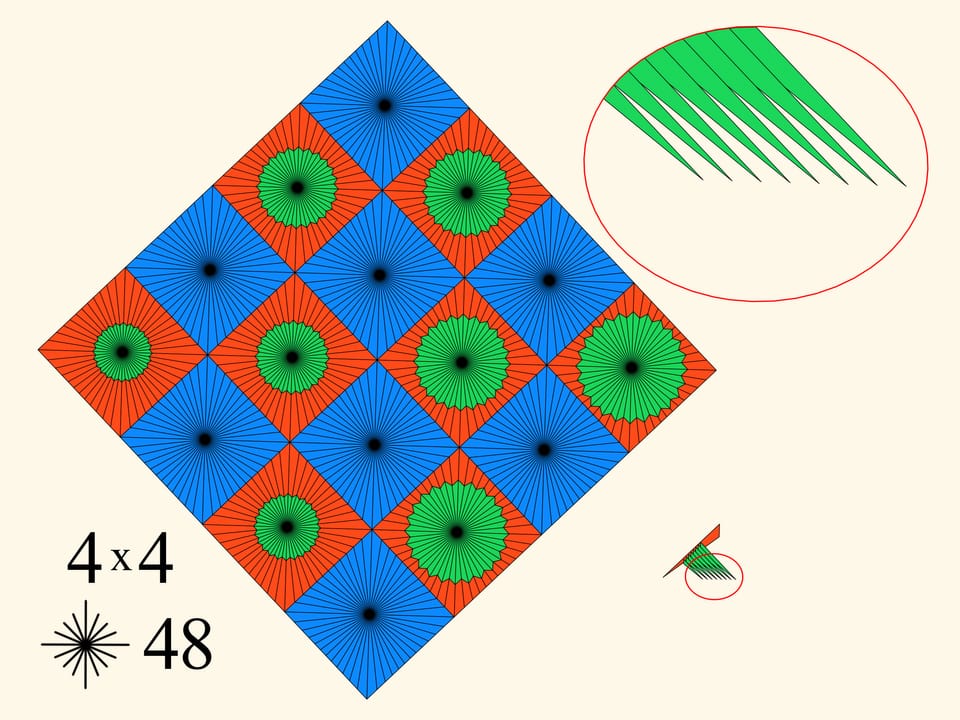
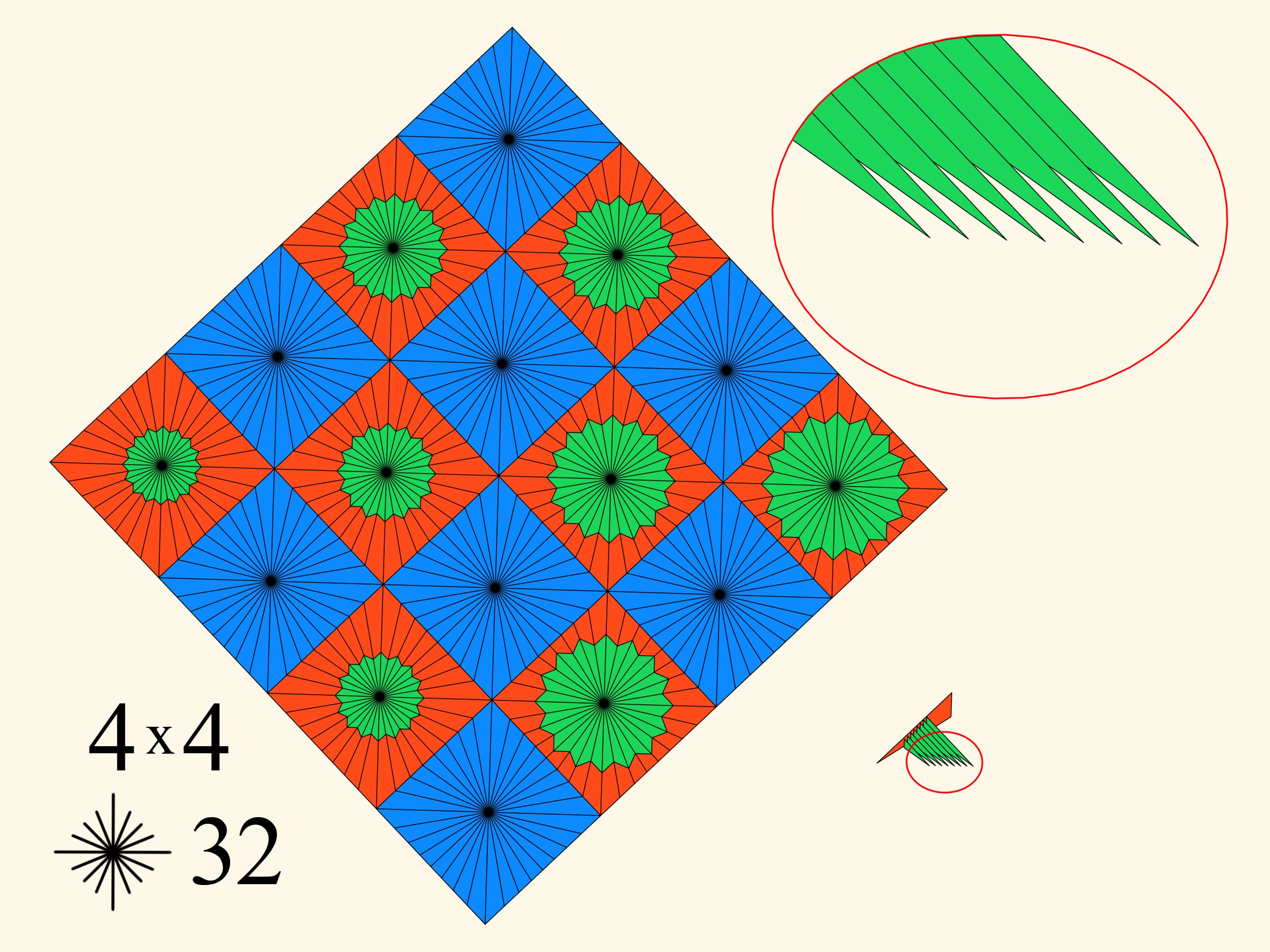
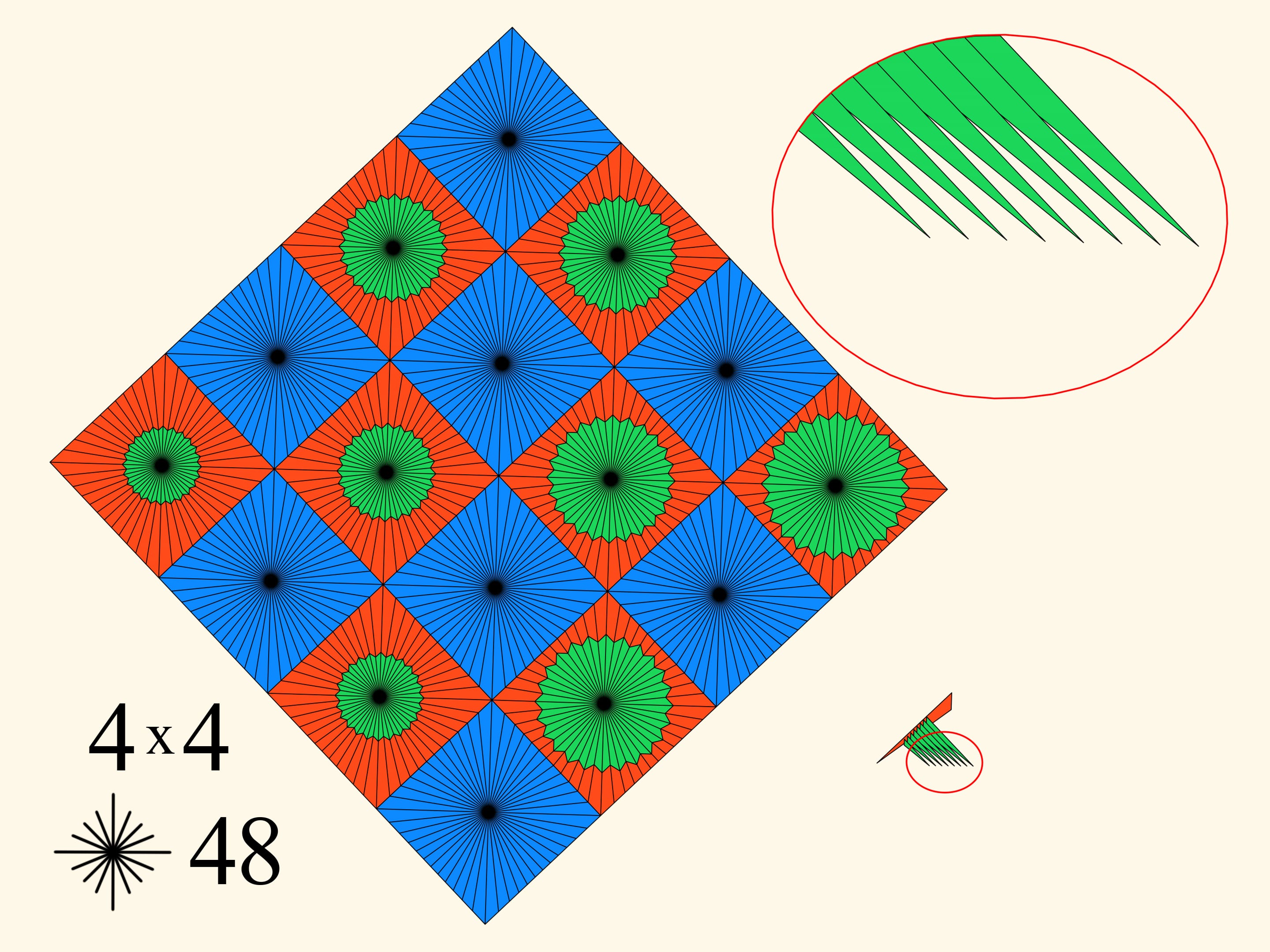
Pour la même subdivision 4x4 on va augmenter le nombre de rayons dans chaque carré. Cela conduit à un amincissement des dents du peigne, à une diminution de l’intersection d’entre eux, et par conséquent, à une croissance modérée du périmètre.
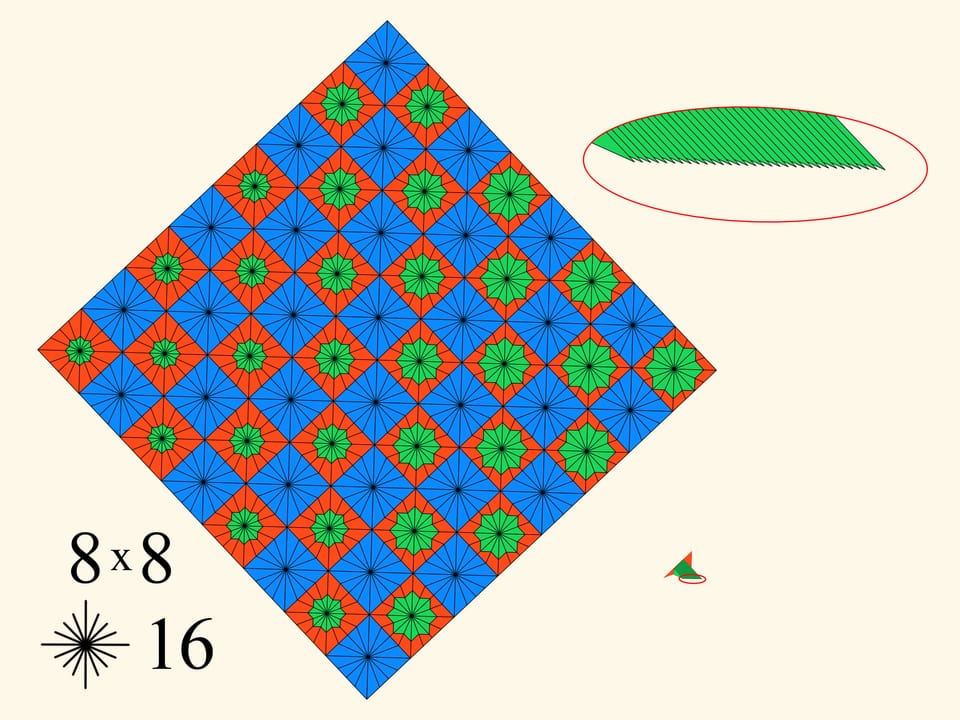
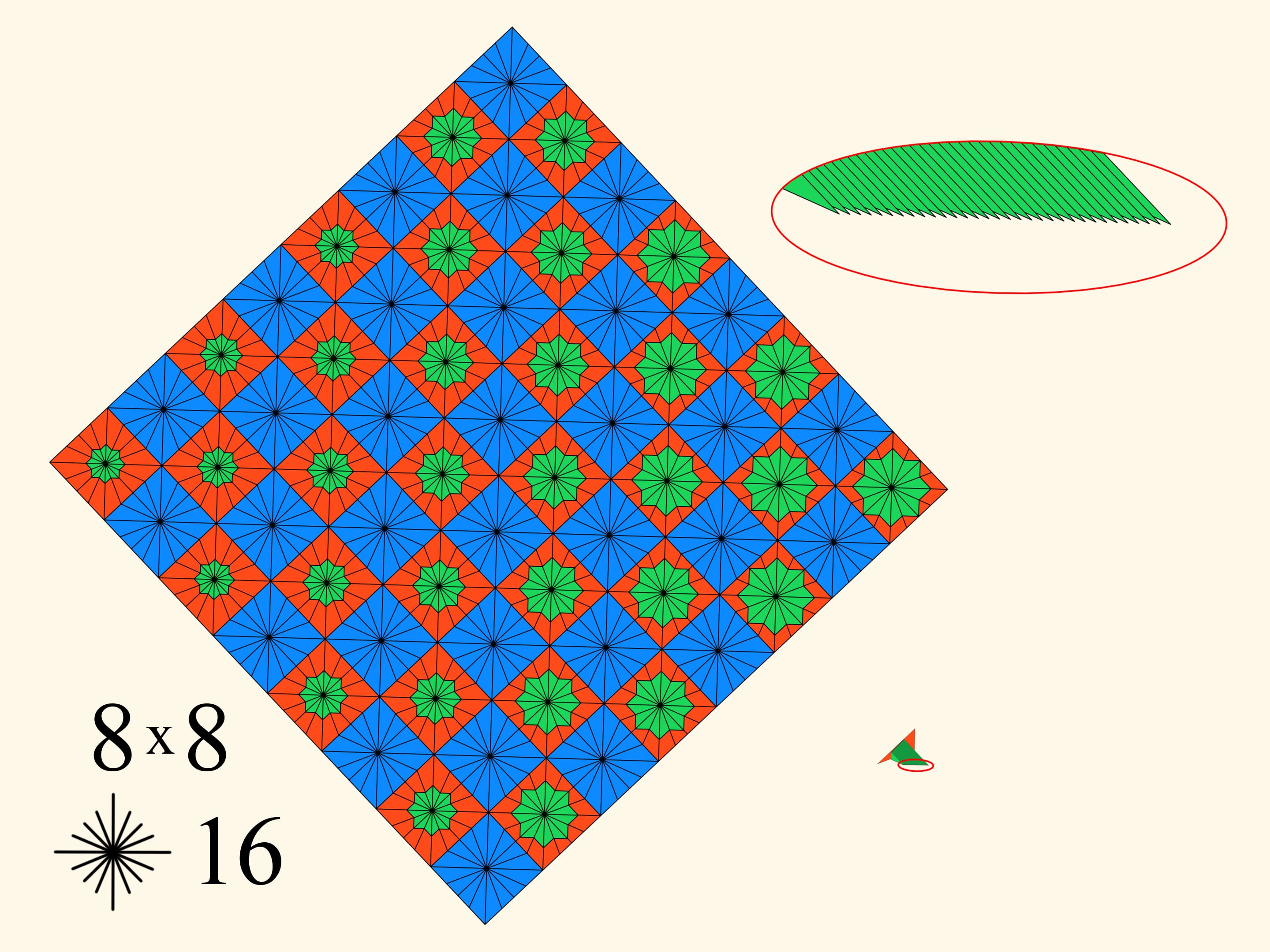
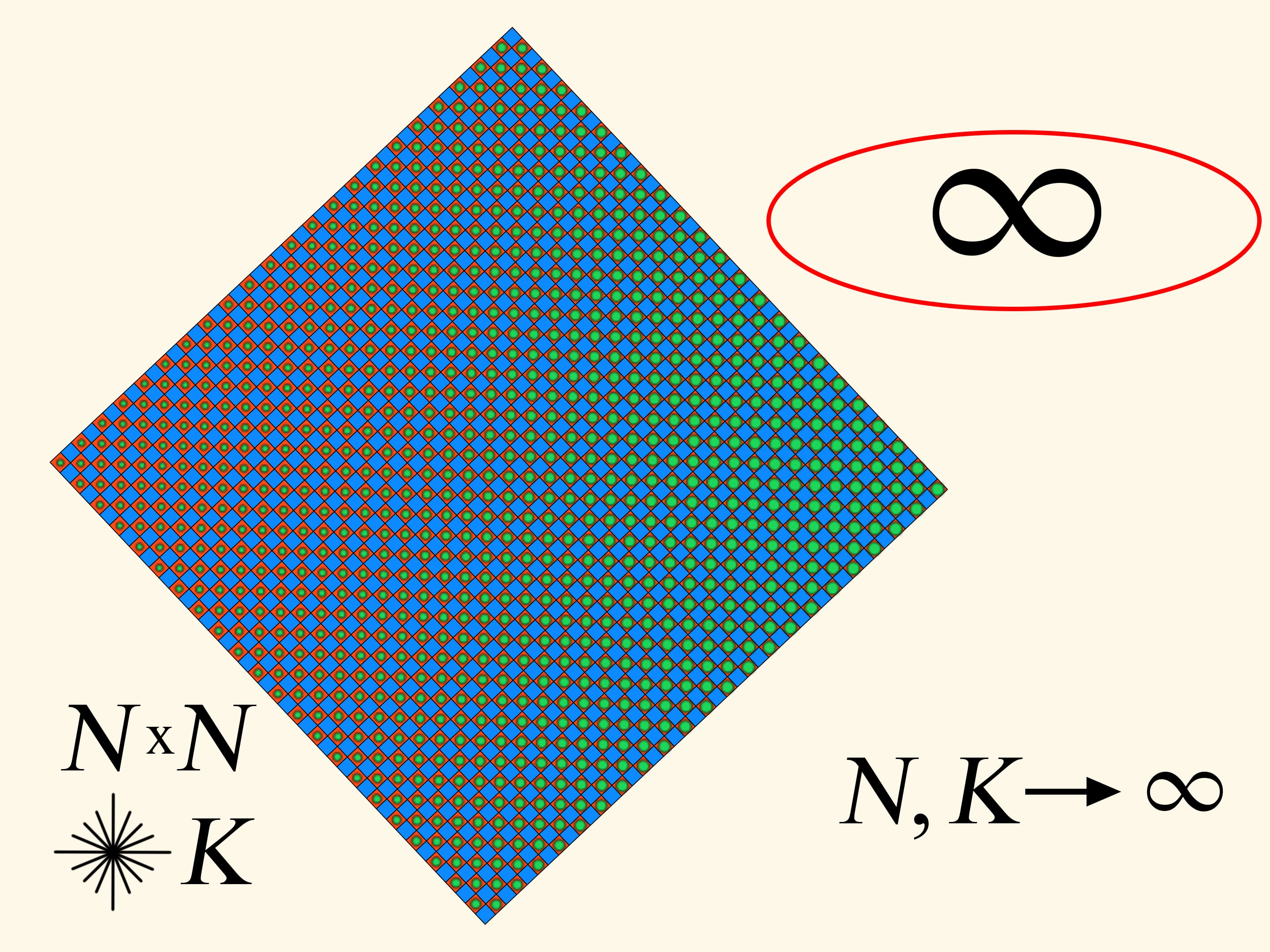
Il y a encore un autre paramètre, le nombre de cases qui composent le carré initial. Si nous faisons augmenter ce paramètre, le nombre de dents du peigne de la construction va augmenter.
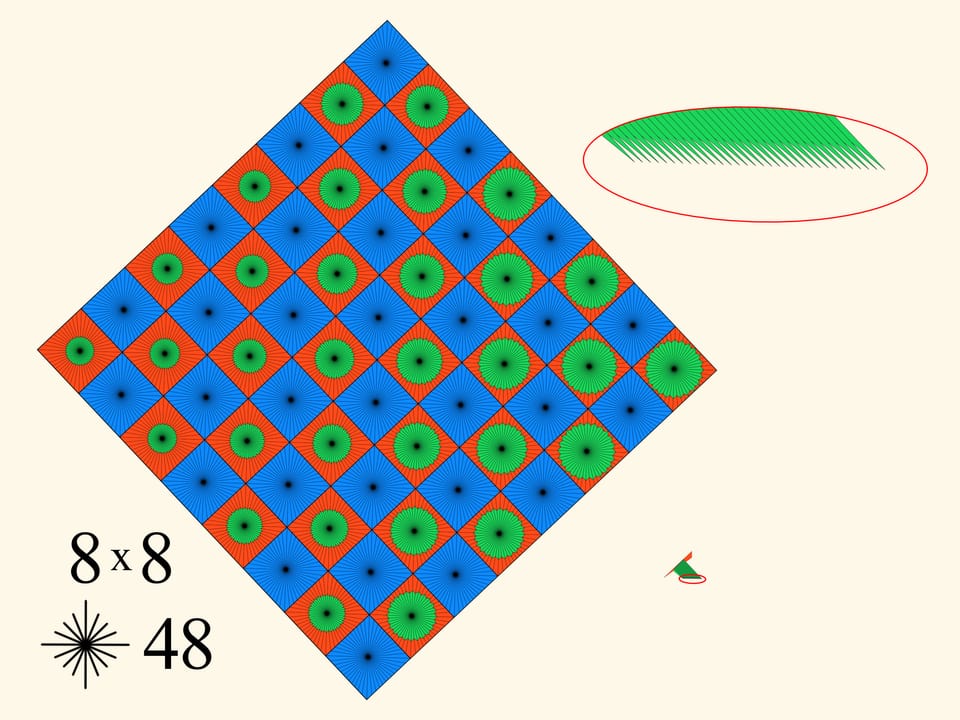
L’augmentation simultanée des deux paramètres, le nombre de cases et la quantité de rayons — donne une augmentation du périmètre. Mais combien peut il augmenter? On trouve, jusqu’à l’infini. Mais cela signifie qu’à un certain moment il dépassera le périmètre du carré initial!
Le problème du rouble replié — plier un rectangle en augmentant son périmètre — est résolu. Mais combien de fois faudra–t–il plier? Pas mal. Depuis les travaux de A. Tarasov voila une réponse: pour une subdivision du carré en 16x16 cases et un nombre de rayons dans chaque case de 16²•30, le périmètre du polygone obtenu sera plus grand que le périmètre du carré initial.
Dans le film, on ne peut pas montrer cela, mais est–ce que l’on peut obtenir dans la réalité? Sûrement vous vous souvenez bien que plier une feuille de papier, bien que très fine, c’est possible au plus 7–8 fois. Si vous ne l’avait pas fait depuis longtemps, essayez–le avec une simple expérience. Alors, qu’est ce que le problème posé par V.I. Arnold, et cette solution avec un algorithme “pas réalisable”, nous donne? Certainement, un instrument de progrès dans la science, qui sera certainement utile dans le développement futur.