Les développements des polyèdres les plus courant,s pour nous, ne ressemblent pas toujours à ce qu’on croit. Est-ce possible d’obtenir un tétraèdre régulier à partir d’un morceau de carton?
On déplie un tétraèdre selon le développement le plus courant.
Traçons une partie d’angle d’un grand triangle jusqu’au centre du côté opposé (le sommet du tétraèdre donc de départ) et découpons, selon lui, notre morceau de carton. Plions une partie du patron en suivant les points, répondant au sommet du tétraèdre. Avec cela, nous collons deux arêtes, initialement collées, c’est pourquoi les conditions de collage des côtés de notre patron ne sont pas troubles. A présent, on ajoute un morceau de côté qui n’était pas présent dans le développement initial. Nous marquerons cette “fausse” arête de couleur rouge.
Recommençons l’opération encore une fois.
Retraçons un segment de l’angle, jusqu’au côté opposé, et découpons selon le tracé. Faisons le contour et le collage. On obtient alors le même morceau de carton que celui du désert de la séquence!
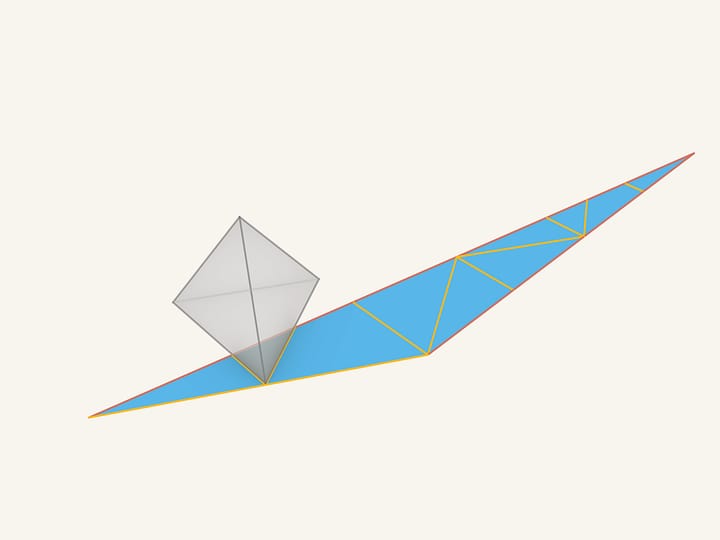
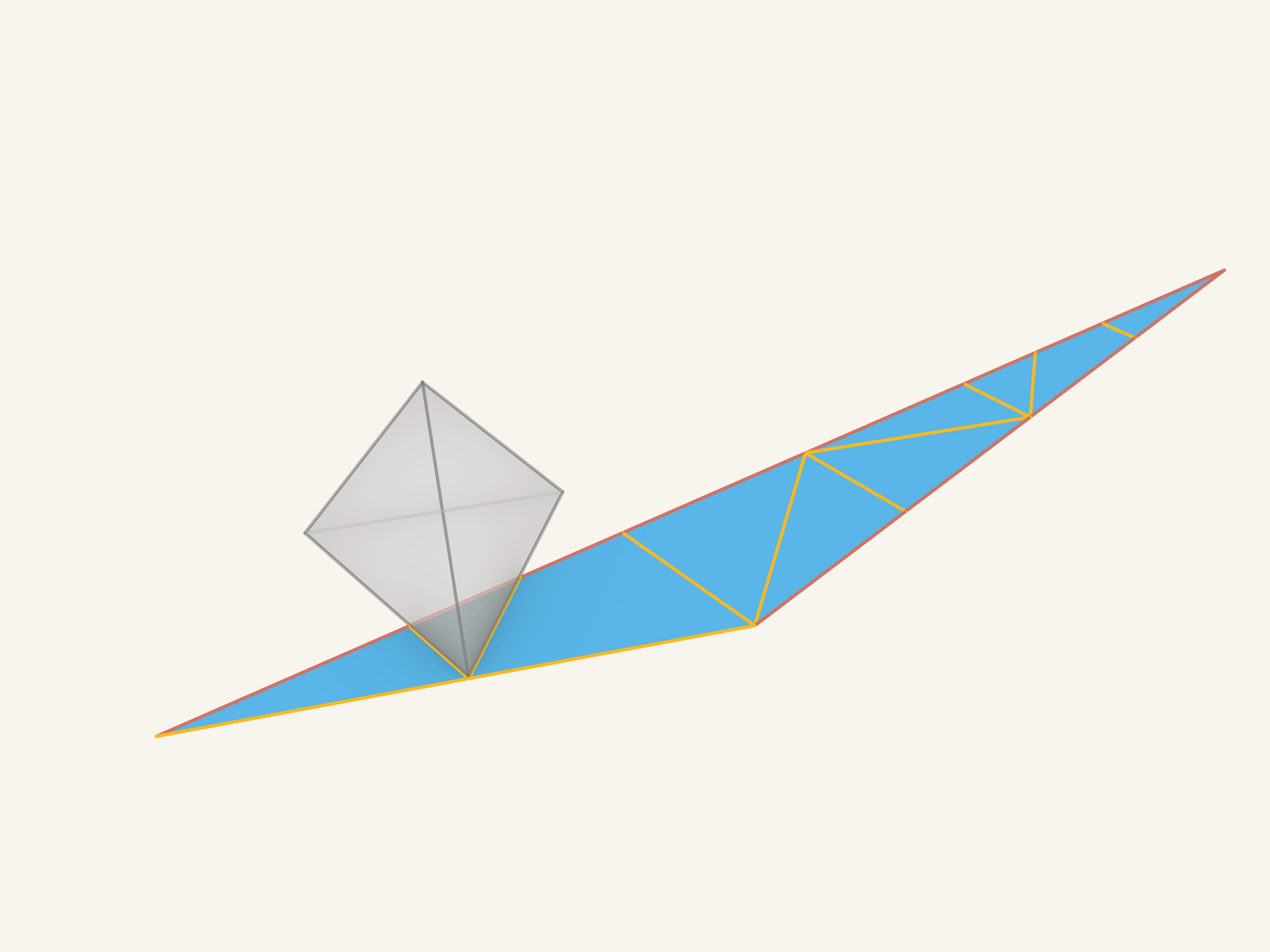
Assurons-nous que le morceau de carton obtenu apparaisse bien comme le développement du polyèdre de départ. Du côté gauche du triangle, il y a des morceaux que nous n’avions pas mis dès le début. Un des petits triangles correspond à la partie de base du tétraèdre initial. Réunissons-les.
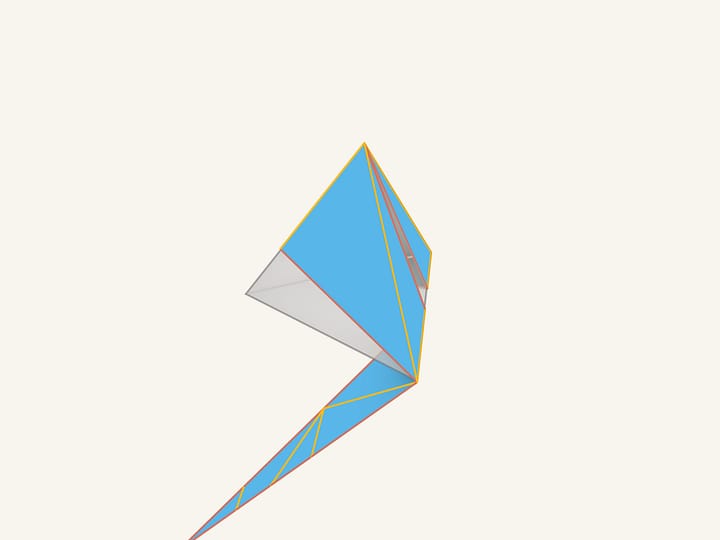
Et maintenant, enroulons notre figure pour en faire un tétraèdre. Comme nous le voyons, tout coïncide!
Tous les segments des arêtes rouges, les “faux”, se retrouvent en triangles réunis, sur un même plan. Cela signifie qu’après le collage, ces arêtes disparaitront. Ces mêmes segments qui étaient colorés en jaune, recouvrent les arêtes du tétraèdre et apparaissent comme de véritables arêtes..
A la question “est-il possible de faire un polyèdre en relief à partir d’un morceau de carton donné?” répond le théorème d’un grand géomètre russe, Alexandre Danilovitch Alexandrov. On peut comprendre où seront les sommets de ce polyèdre. Et voilà comment les vraies arêtes, dans un cas général, passent entre les sommets. Jusqu’à présent, les mathématiciens ne savent pas démontrer cela. Mais c’est déjà une autre histoire, pour une autre Etude…