Le developpement ⁠

Qu’est-ce donc que le dévelop­pe­ment d’un polyèdre? Vous diriez que c’est un morceau de carton à partir duquel on peut former un polyèdre donné. C’est en partie vrai, mais ce n’est pas toute la vérité. Il est montré que la notion de dévelop­pe­ment contient beau­coup plus qu’un simple morceau de carton.

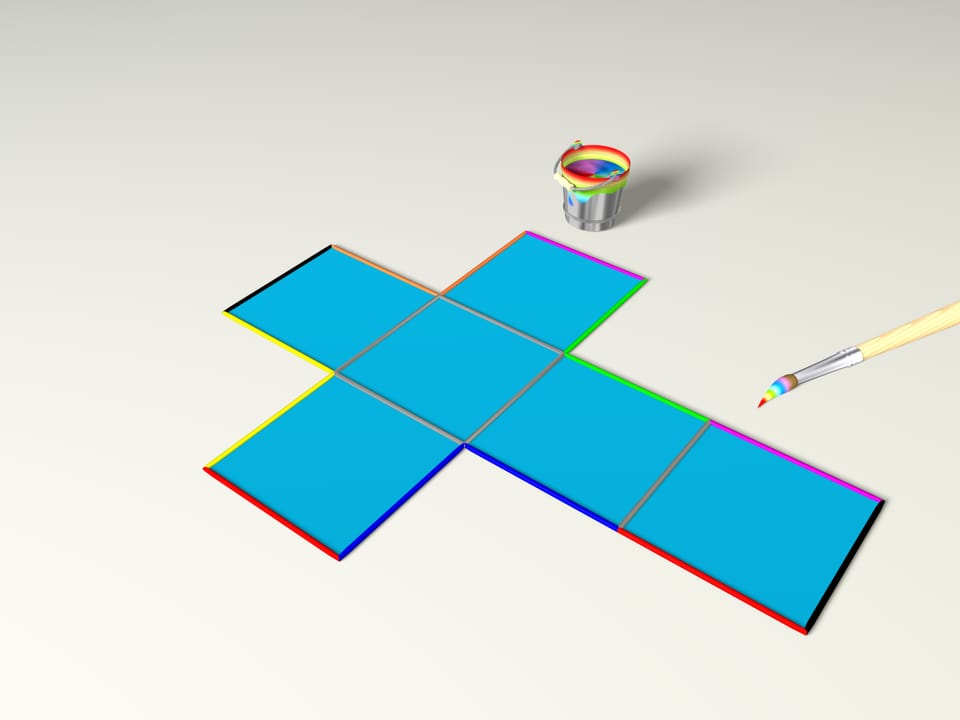
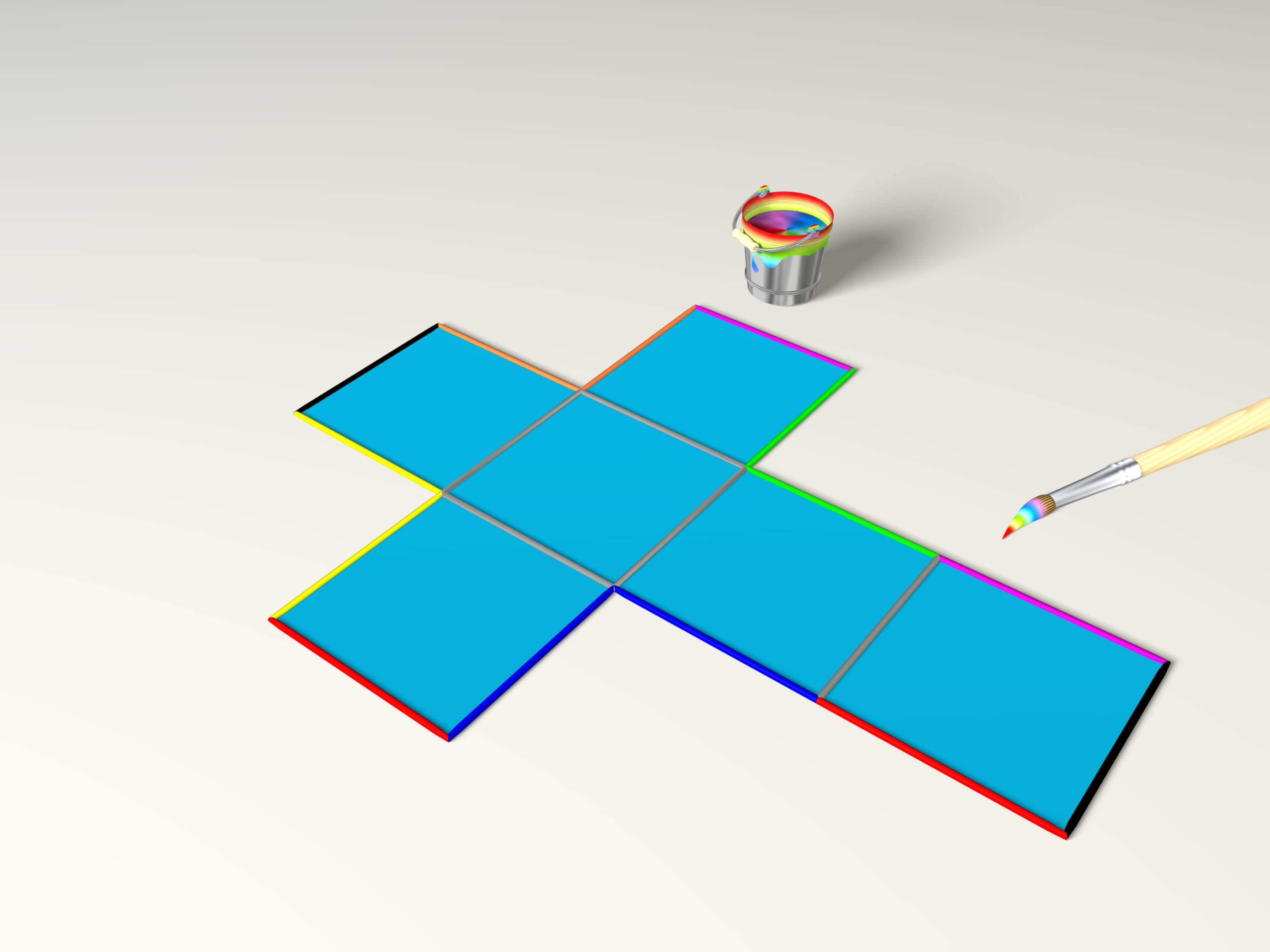
Quel polyèdre peut-on former à partir de la célèbre croix latine? Bien sûr, un cube. Pour cela, il faut colorer les arêtes, comme l’a fait le pinceau magique (les arêtes d’une seule couleur se collent sur le polyèdre, les unes aux autres).

En fait, bien sûr, il aurait été préférable de colorer non pas les arêtes, mais chaque paire de points de différentes couleurs. On pose, comme on dit en mathématiques, les condi­tions de collage des côtés.

Après avoir posé les condi­tions de collage, les arêtes passant à l’intérieur du morceau de carton, définies à un chiffre, selon le théorème de A.D. Alexan­drov.

Ainsi, on peut plier la croix pour faire un cube.

Mais il apparaît que si les condi­tions de collage des côtés sont posées différemment, alors on peut obtenir tout à fait autre chose qu’un cube!

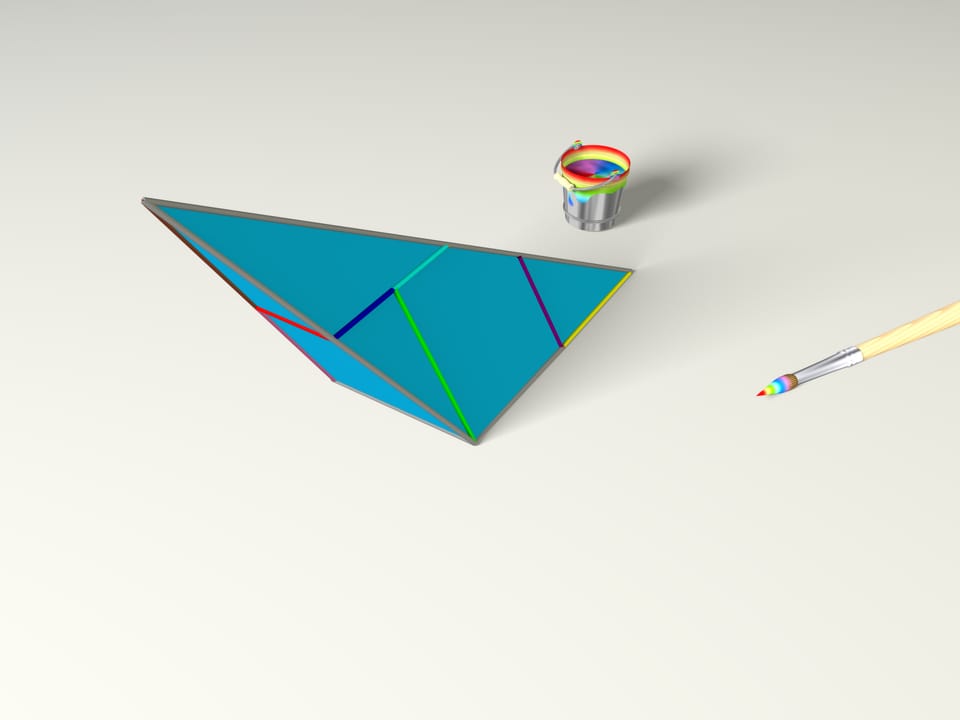
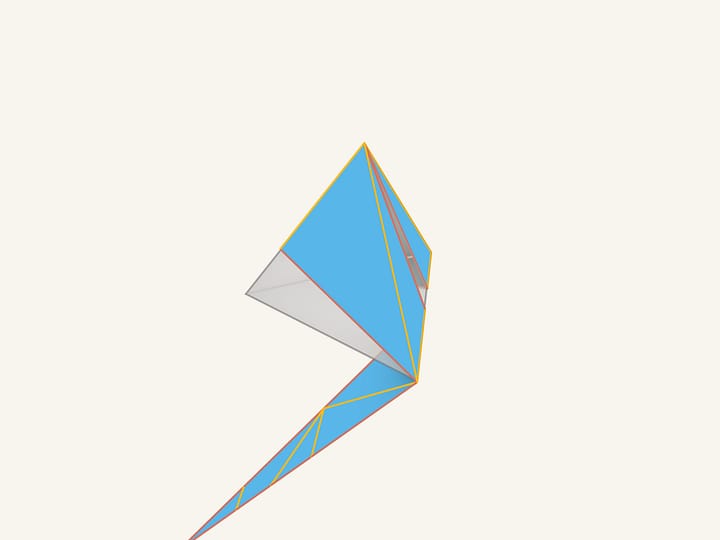
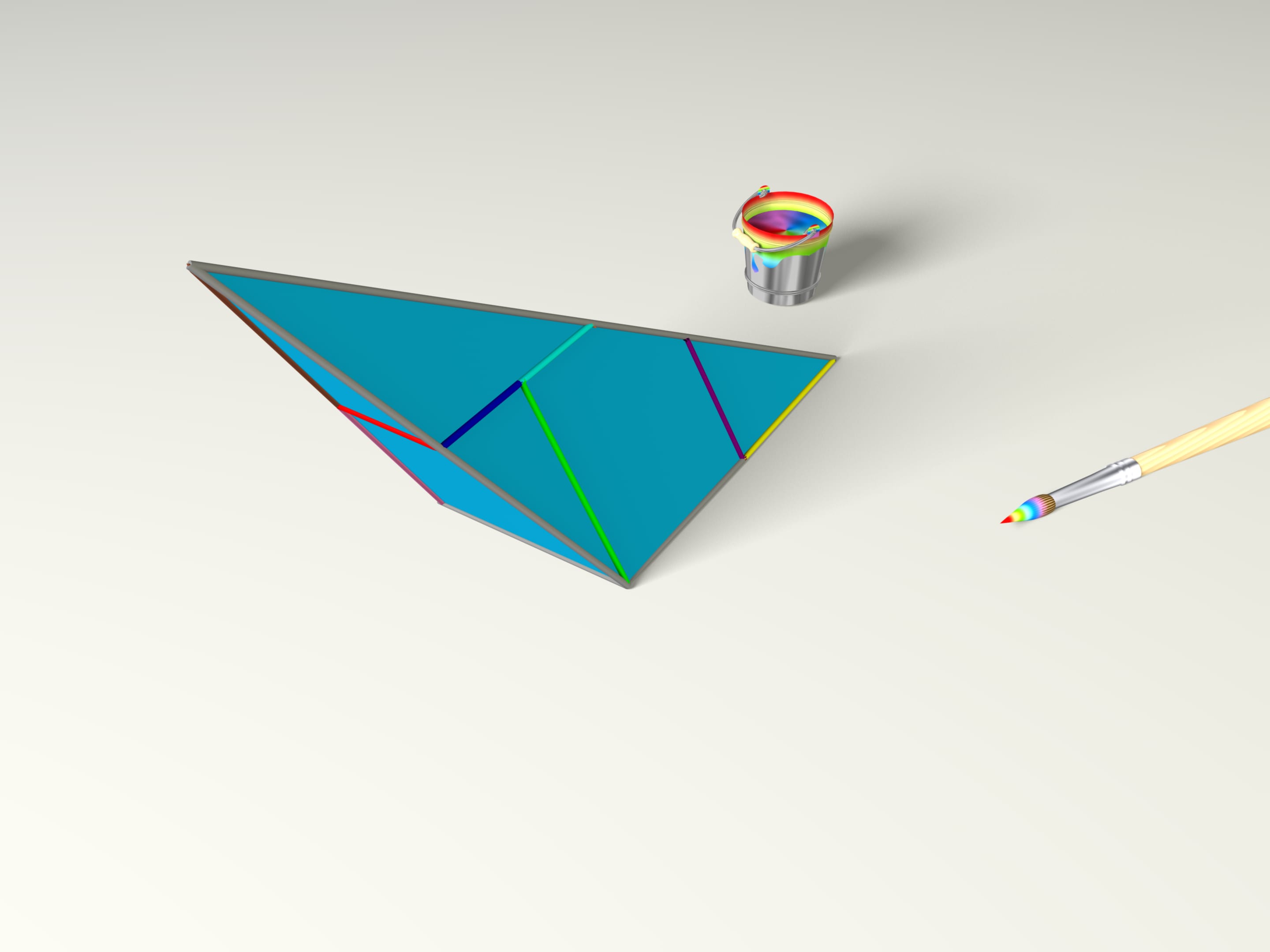
Notre pinceau magique a coloré les arêtes de cette façon. Encore un batte­ment et nous connais­sons déjà comment ont été définies les arêtes à l’intérieur du morceau de carton. Si main­te­nant, suivant la condi­tion dessinée de collage, on plie un polyèdre, alors on obtiendra une pyra­mide!

Il n’y a pas si long­temps qu’on a démontré qu’en donnant des condi­tions différentes de collage des côtés d’une croix latine, on peut la plier en cinq types de polyèdres convexes.

Ainsi, comme on a pu s’en convaincre, la notion de dévelop­pe­ment inclut, non seule­ment un morceau de carton, mais égale­ment les condi­tions de pliage de ses côtés. Si les dernières ne sont pas définies, alors on peut obtenir, à partir de n’importe quel morceau, des polyèdres convexes différents.