Projeter un rayon ⁠

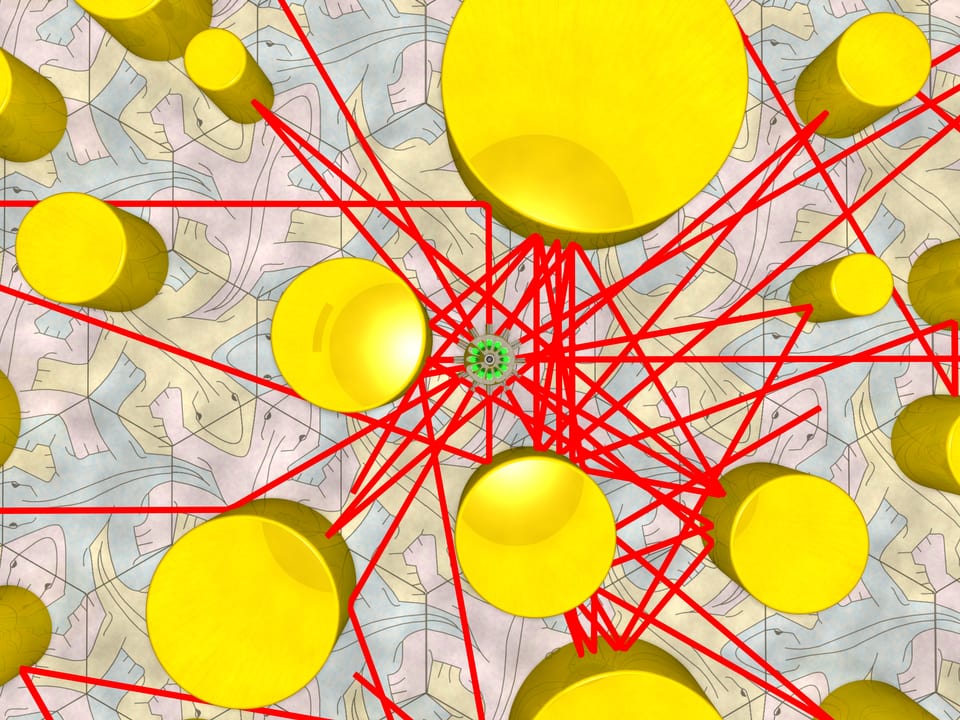
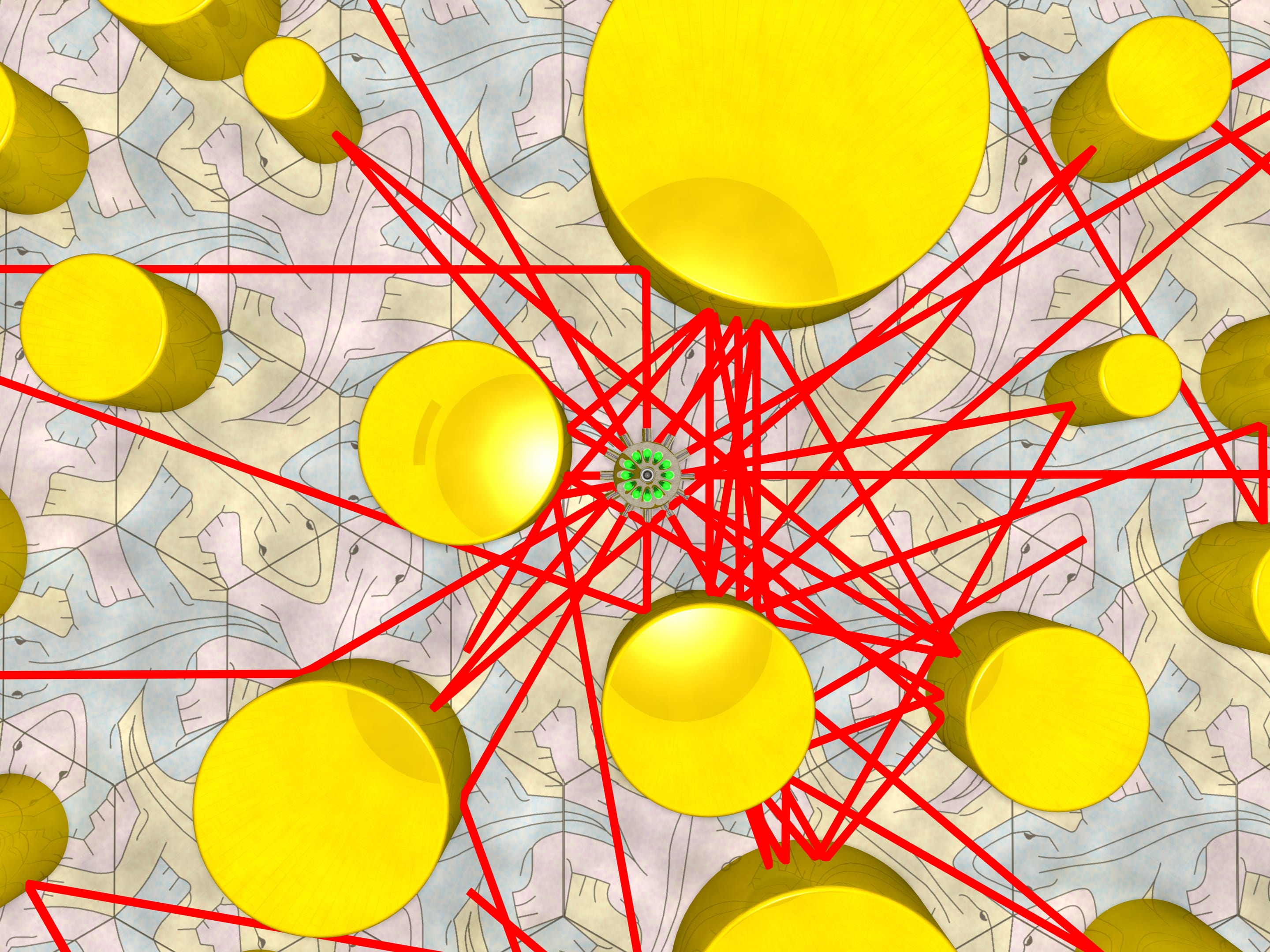
Peut-on placer des colonnes rondes en miroir, afin qu’un rayon, parallèle au sol, n’atteigne les murs dans aucune des direc­tions initiales? Les colonnes, recou­vertes d’un miroir cylin­drique, peuvent être de n’importe quel  diamètre, et disposées à n’importe quel point, à condi­tion qu’elles ne se croisent pas entre elles ( la résolu­tion est alors triviale).

On sait que le reflet du miroir se produit selon la loi d’égalité entre l’angle d’inci­dence et l’angle de réflexion. Si, par hasard, le miroir n’est pas lisse, l’angle entre le rayon et la surface du miroir s’appelle l’angle avec une surface tangen­tielle, menant à un point d’inci­dence du rayon.

Combien de colonnes faut-il et quelle doit être leur dispo­si­tion pour que le rayon soit projeté, et n’atteigne pas les murs? Y a-t-il un nombre fini de miroirs ou en faut-il une infinité? Et peut-être qu’un nombre infini n’est pas suffi­sant?

On comprend qu’une colonne ne suffit pas. Le rayon peut passer près d’elle, et quand bien même il tombe­rait sur la colonne, après réflexion,  il attein­drait le mur, de toutes les façons. Ainsi, peu importe la direc­tion empruntée, le rayon touche­rait le mur.

Evidem­ment, deux ou trois colonnes ne sont pas suffi­santes car le mur serait visible du centre de la salle, dans plusieurs direc­tions. Cela signifie que le rayon, lancé dans ces direc­tions, touche­rait le mur.

L’intui­tion nous dit qu’une petite quantité de colonnes n’est pas suffi­sante pour le blin­dage du rayon, et l’expérience nous le prou­vera.

Dispo­sons de nombreuses colonnes et proje­tons des rayons dans toutes les direc­tions. L’expérience montre que les rayons atteignent les murs.

Cepen­dant, l’expérience n’est pas encore une preuve. Peut-être faut-il disposer les colonnes différemment, ou prendre quelques colonnes supplémentaires… Jusqu’à main­te­nant, les mathémati­ciens ne savent pas si une quantité finie de colonnes est suffi­sante pour blinder un rayon. Même s’il y en avait assez, quel devrait être leur diamètre et leur dispo­si­tion? Et peut-être qu’un nombre fini de colonnes ne suffit pas pour la résolu­tion du problème posé?

Peut-être imaginez-vous comment disposer les colonnes?