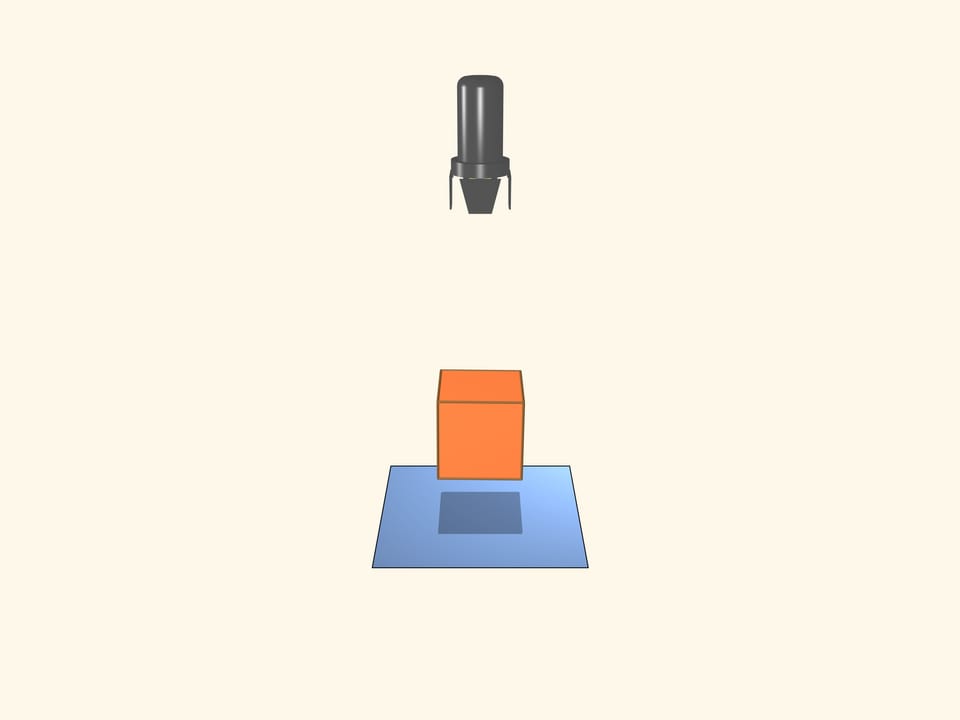
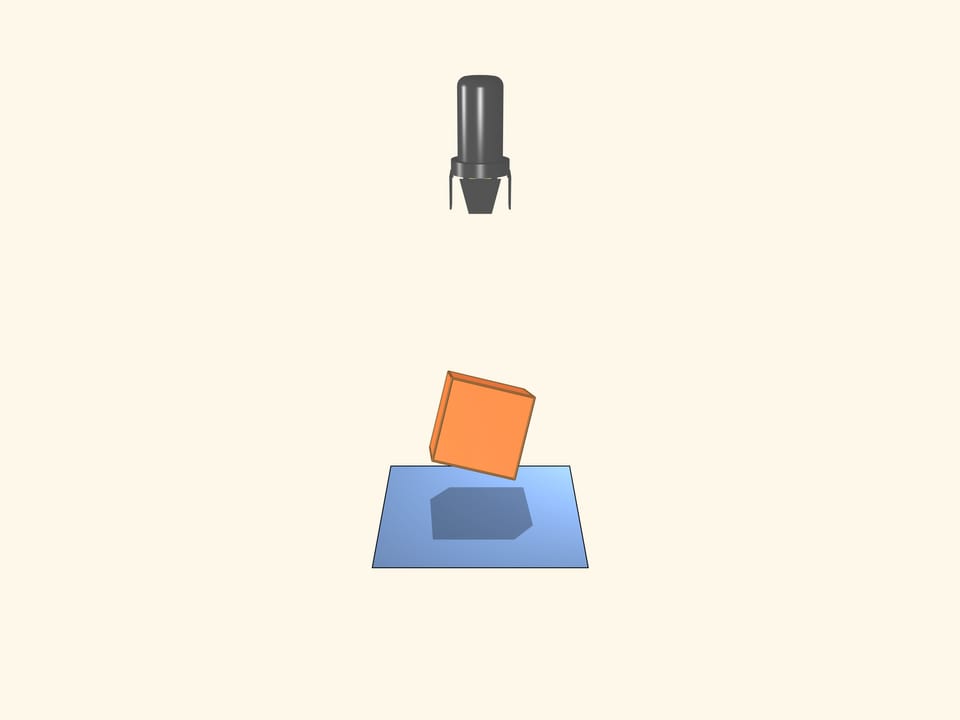
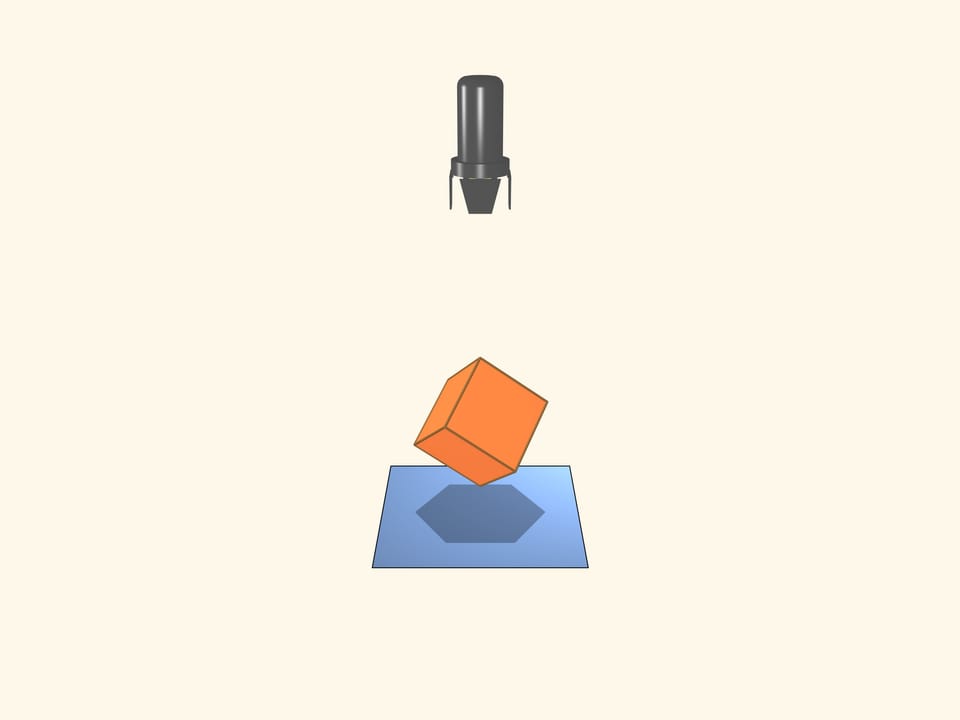
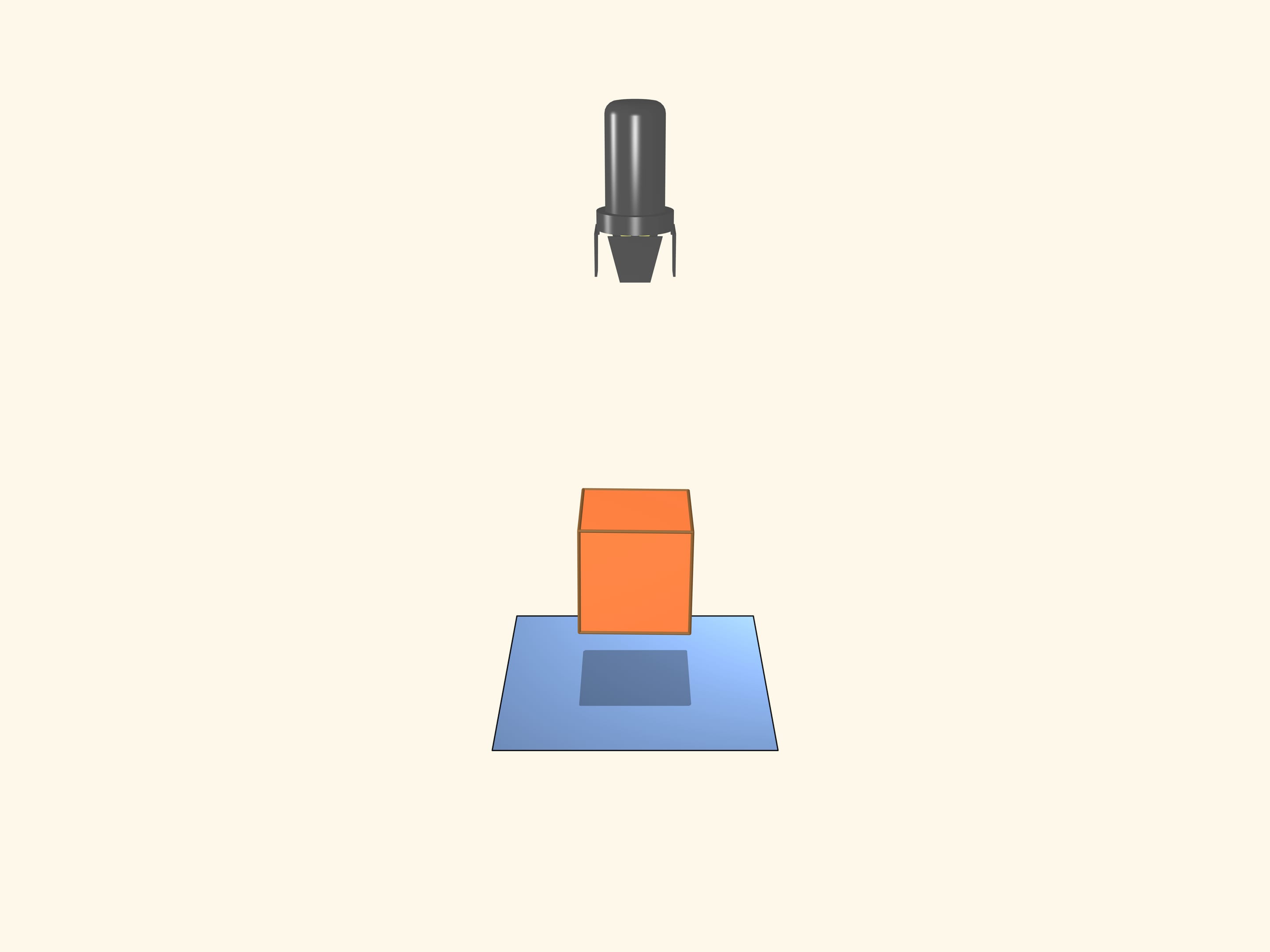
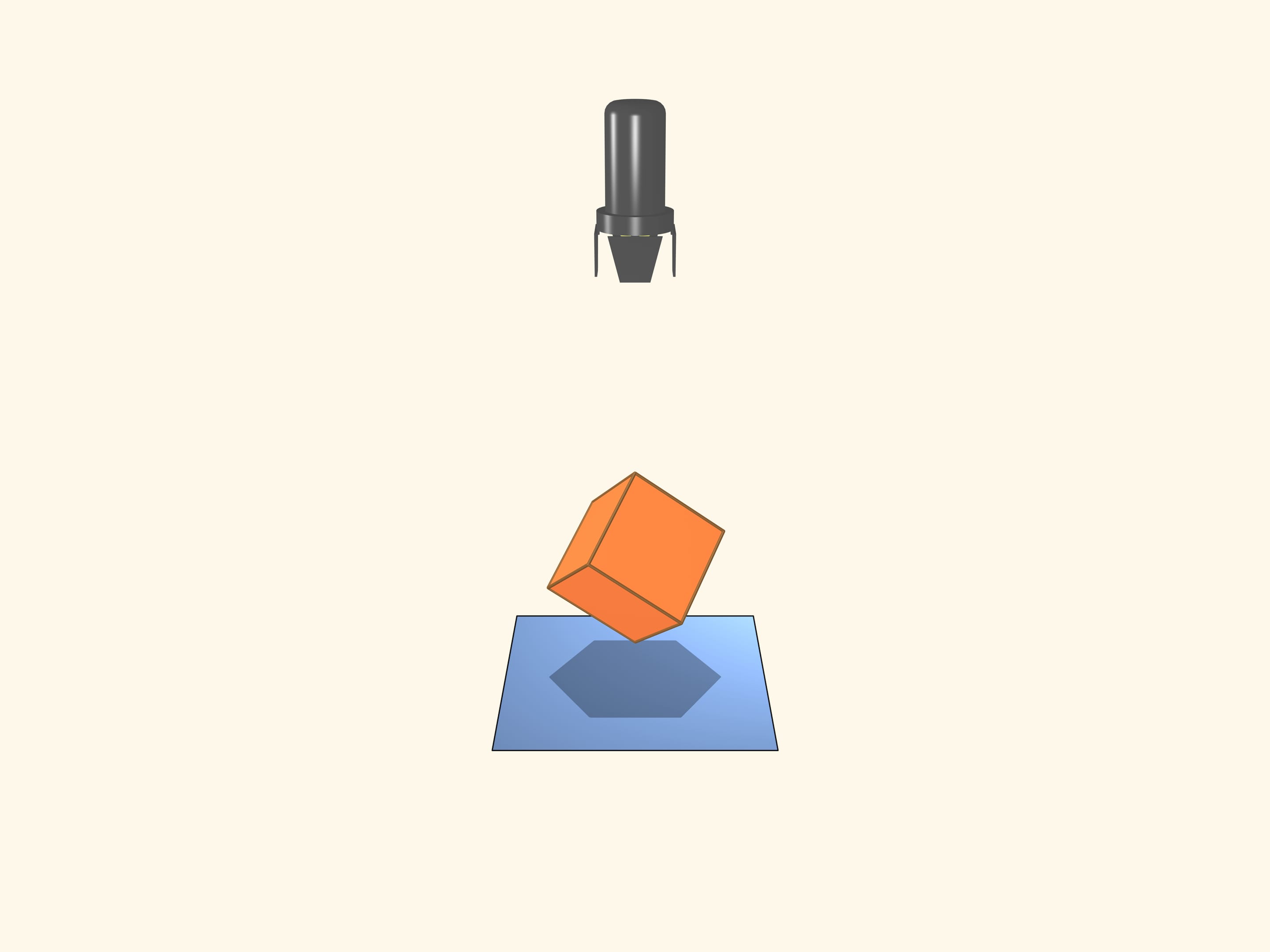
Prenons un projecteur qui éclaire avec des rayons parallèles. C’est évident qu’un cube peut avoir une ombre carré. Combien de sommets au maximum peut avoir le polygone qui forme l’ombre d’un cube? Si la diagonale du cube est parallèle au rayon, l’ombre sera un hexagone régulier.
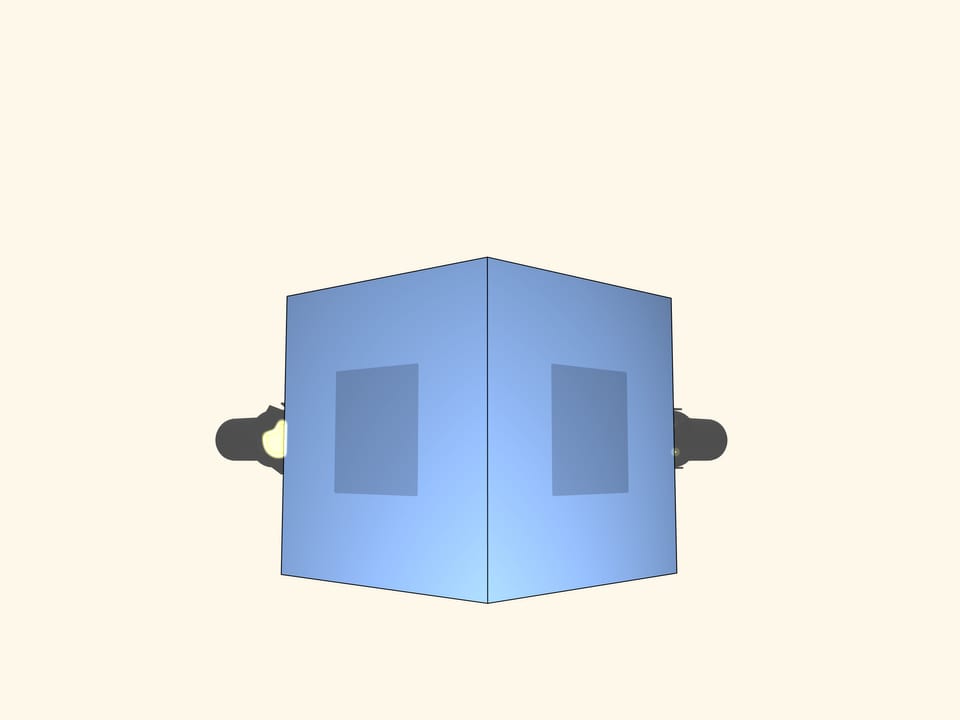
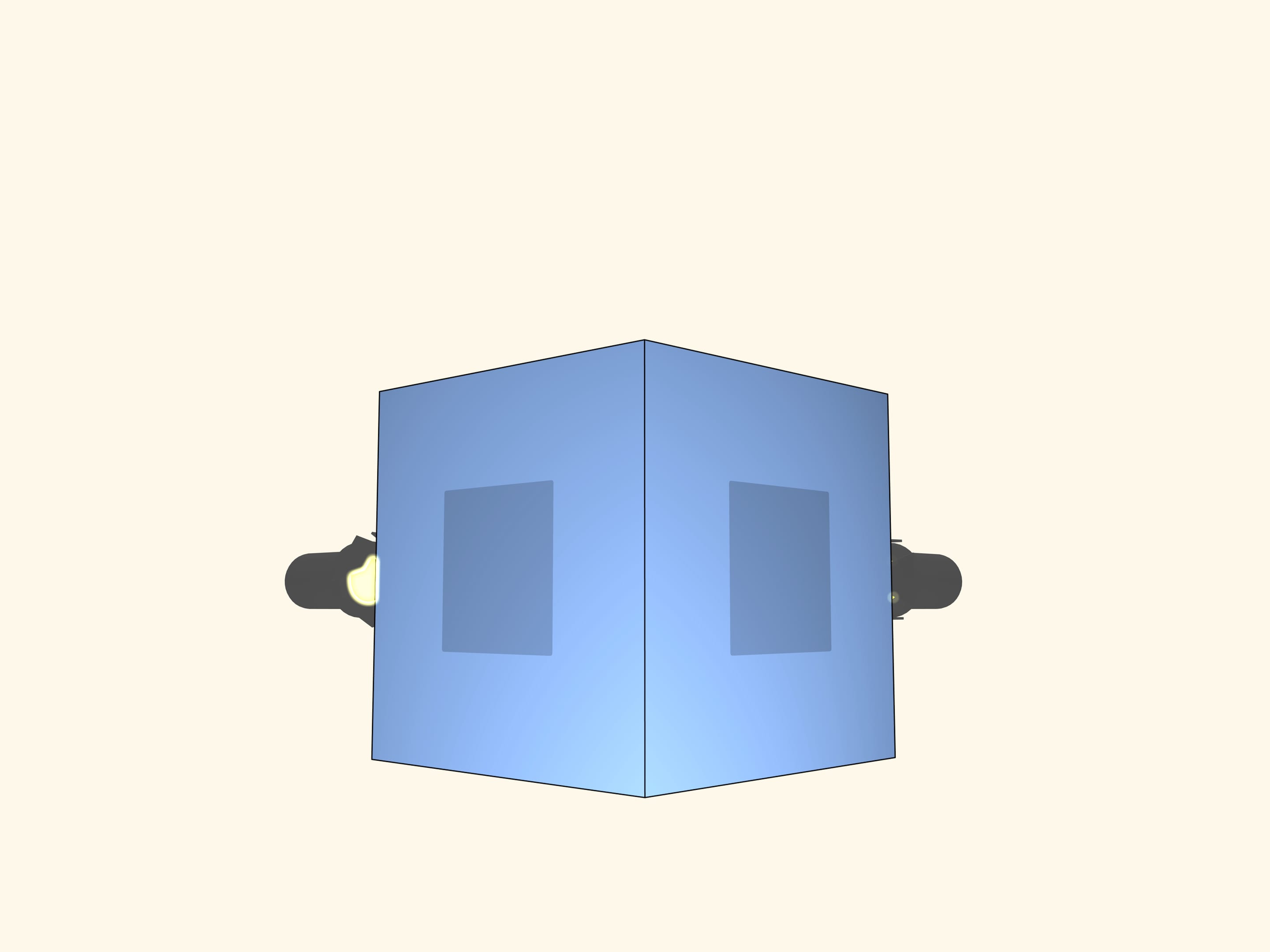
Tournons le projecteur et l’écran. L’ombre qui apparaît sur l’écran est un carré. Notre objet doit-il forcément être un cube?
Ajoutons un écran et un projecteur, perpendiculairement aux premiers. A présent, nous avons 2 projections orthogonales carrées. Le cube est-il le seul à donner de telles ombres?
Et si 3 projections orthogonales étaient carrées.
On peut facilement imaginer des corps non-convexes qui ont de telles projections. Par exemple, un cube avec des imperfections. Mais si on considère uniquement les corps convexes, ou, plus précisément, les polyèdres réguliers, que se passé-t-il?
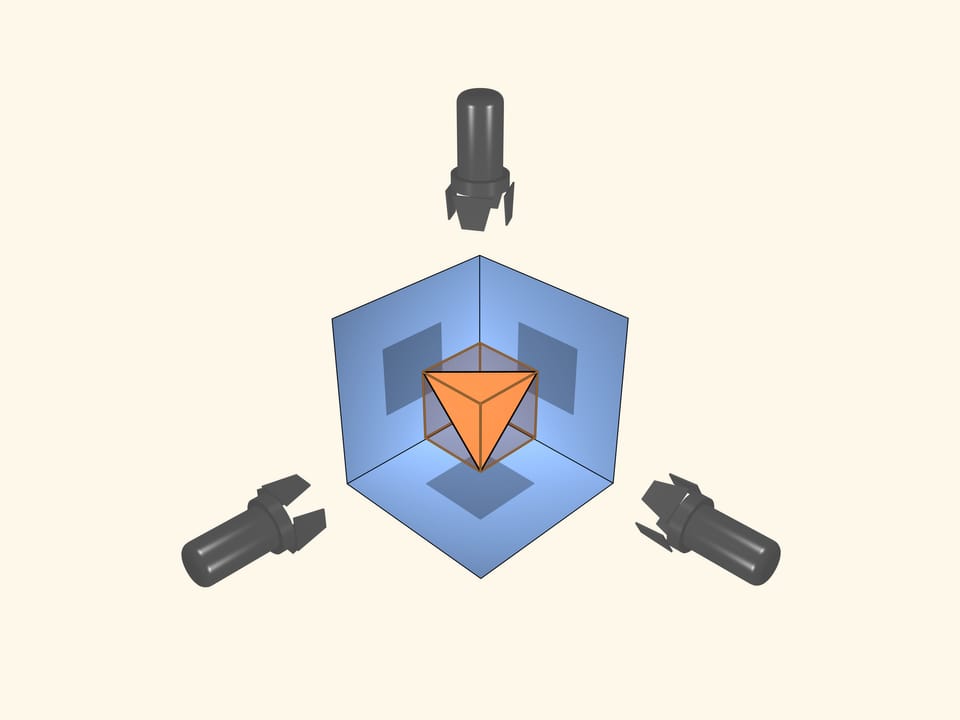
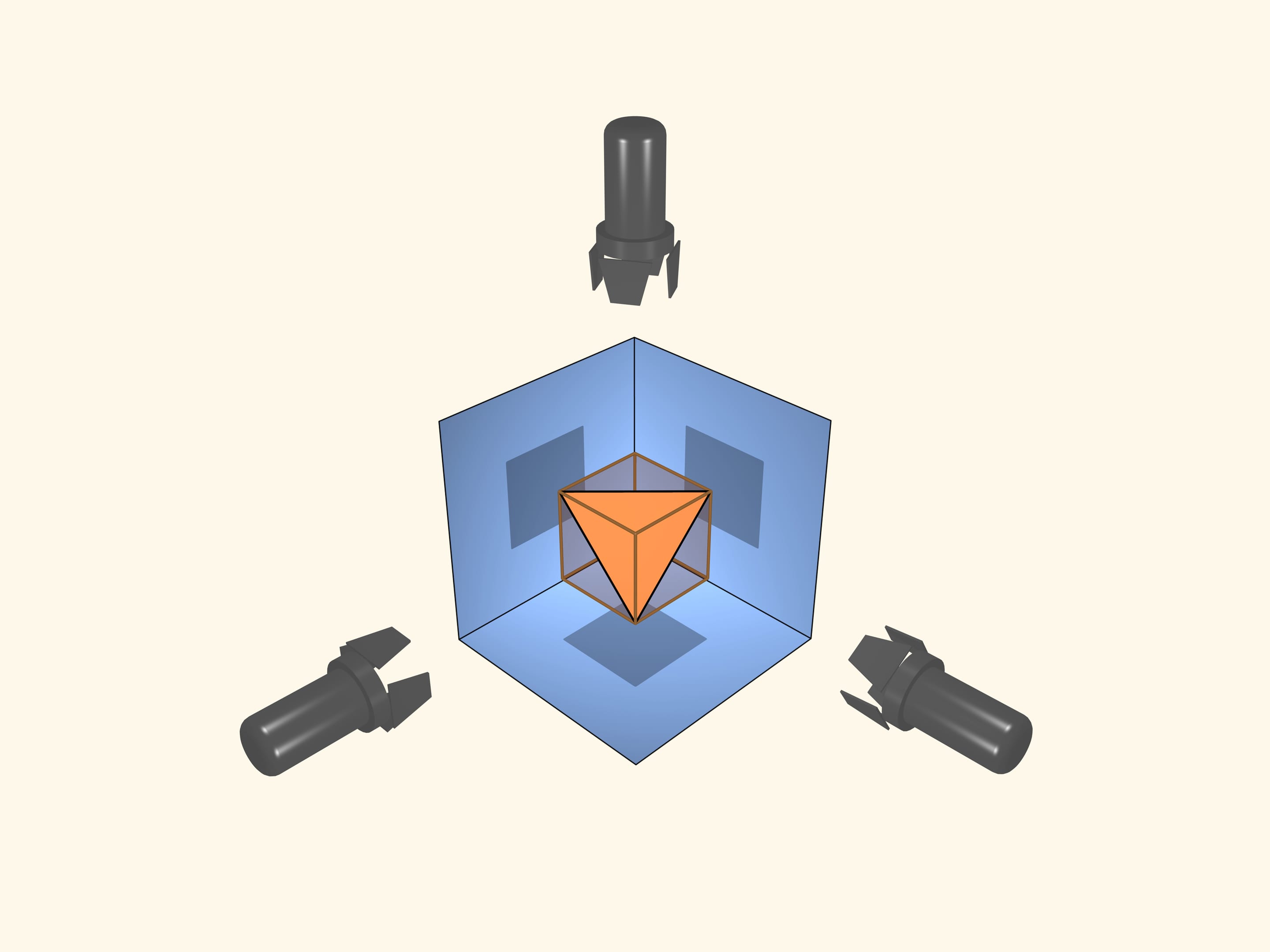
Il se trouve qu’il existe même un polyèdre régulier, autre qu’un cube, donnant des ombres carrées dans 3 directions perpendiculaires.
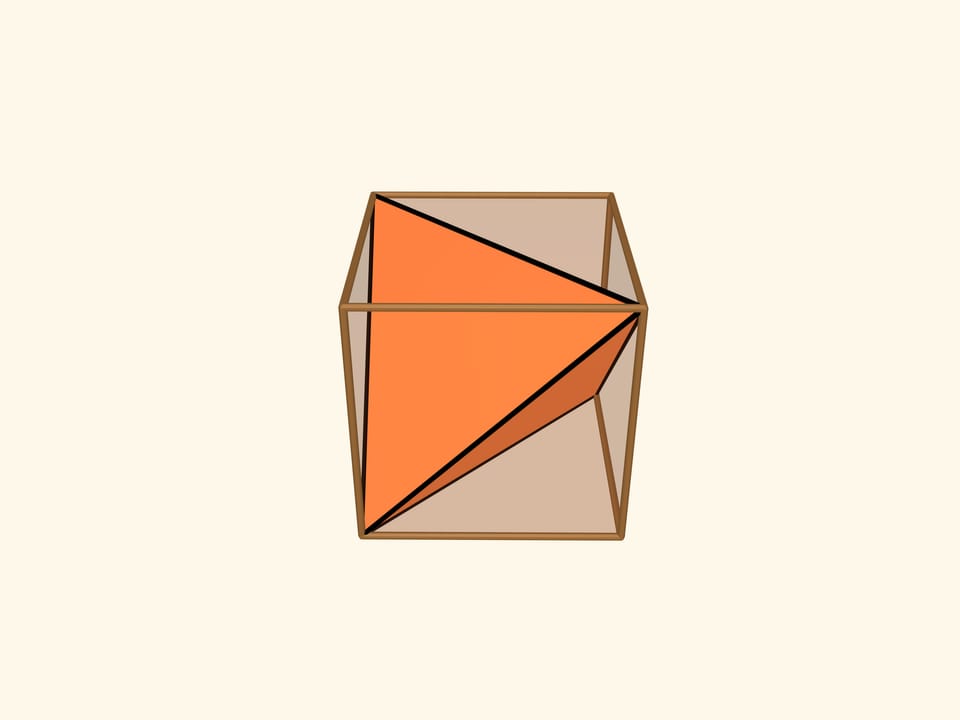
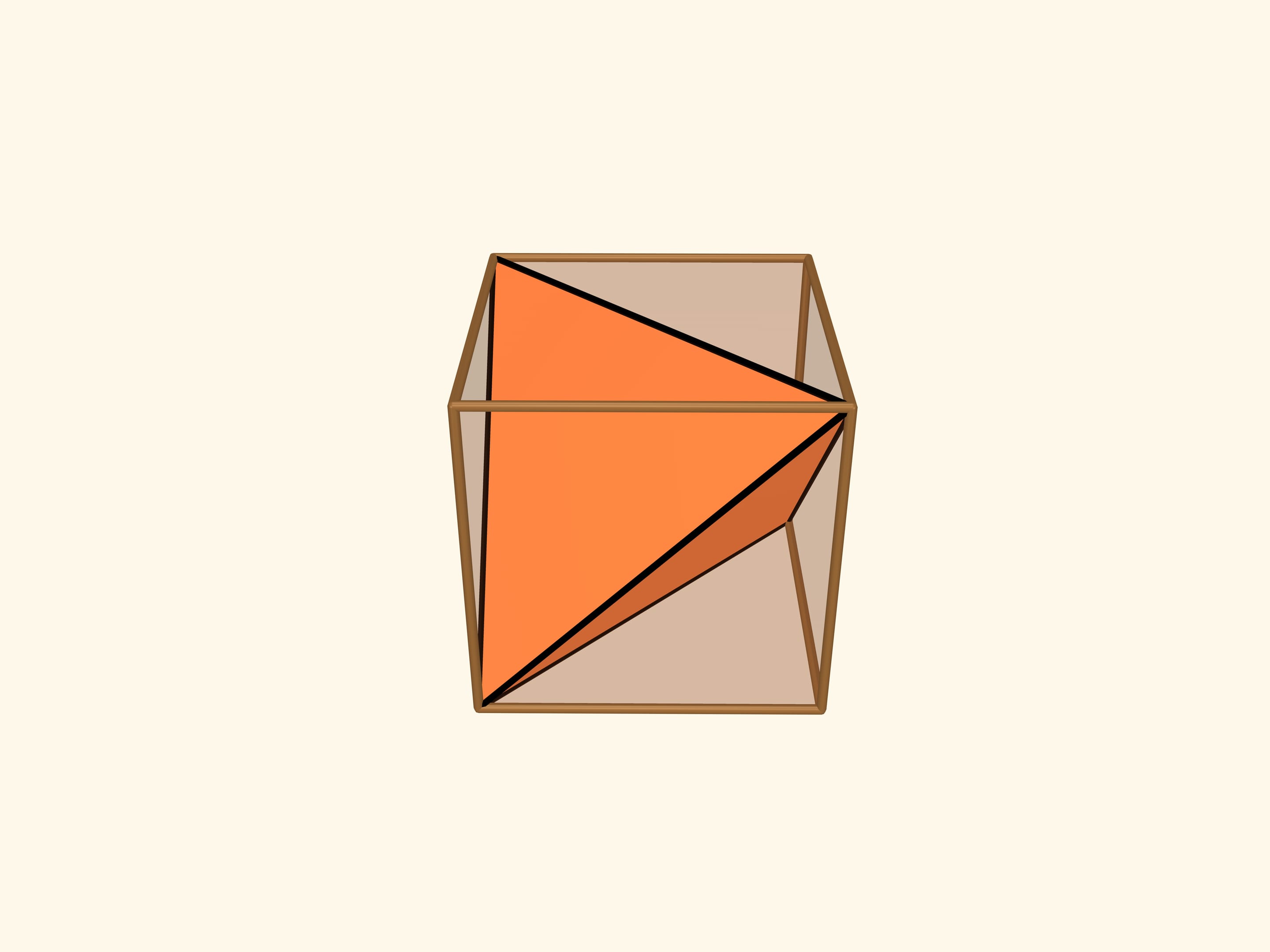
Effectivement, nous pouvons inscrire un tétraèdre régulier dans le cube! Quatre sommets du tétraèdre coïncident avec les sommets du cube. Toutes les arêtes du tétraèdre seront diagonales aux faces du cube et, par conséquent, seront égales entre elles.
Le tétraèdre régulier dispose ainsi occupe toute la projection du cube, dans la direction perpendiculaire de la face.
Si le cube est dispose de sorte que les 3 projections orthogonales soient carrées, le tétraèdre régulier inscrit dedans donnera les mêmes ombres: trois carrés.