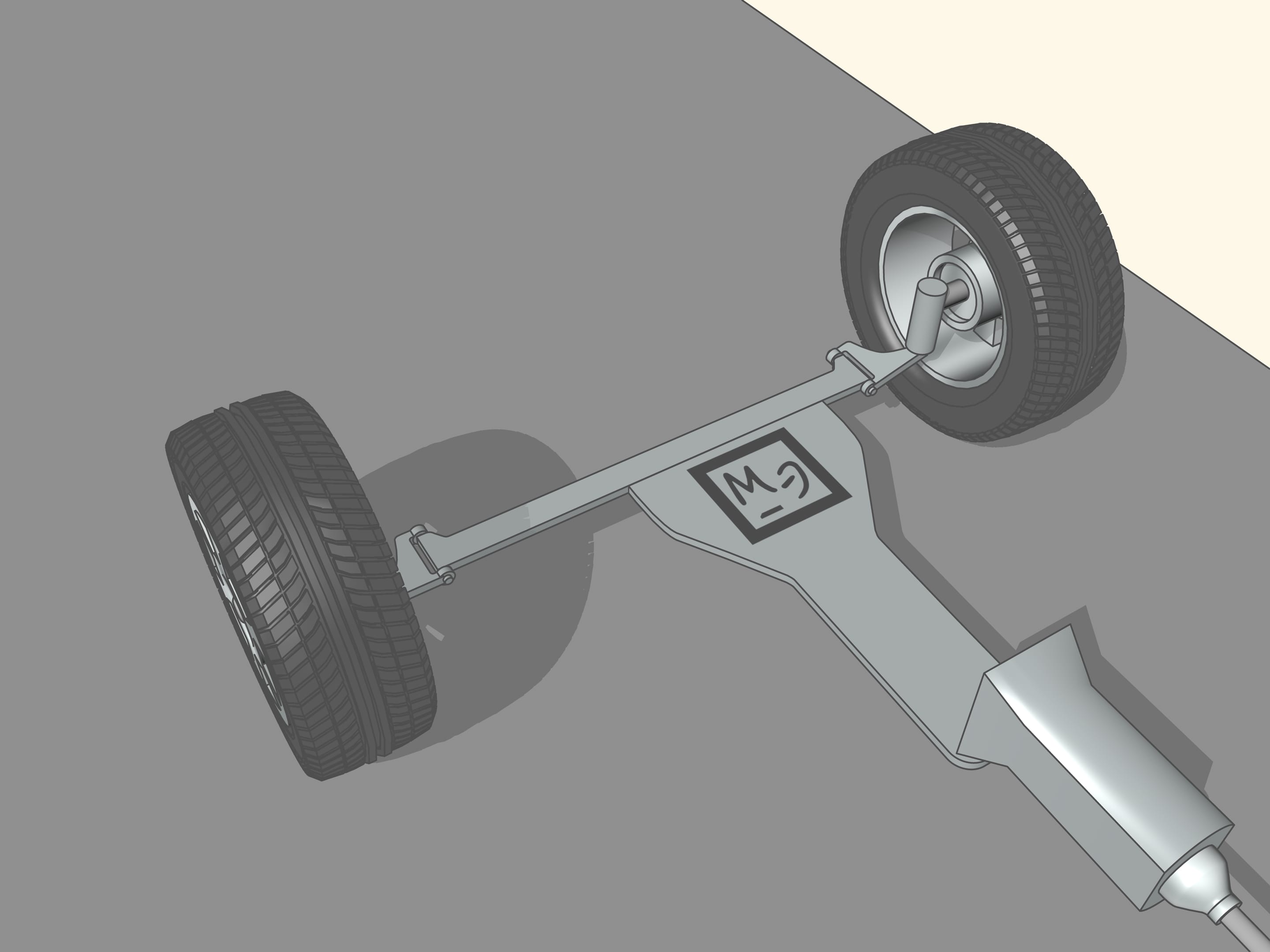
Est–ce que les roues de la voiture sont parallèles lorsque vous braquez?
Il arrive que ce sont précisément la géométrie et la mécanique qui définissent ce qu’il faut faire pour tourner les roues de la voiture.
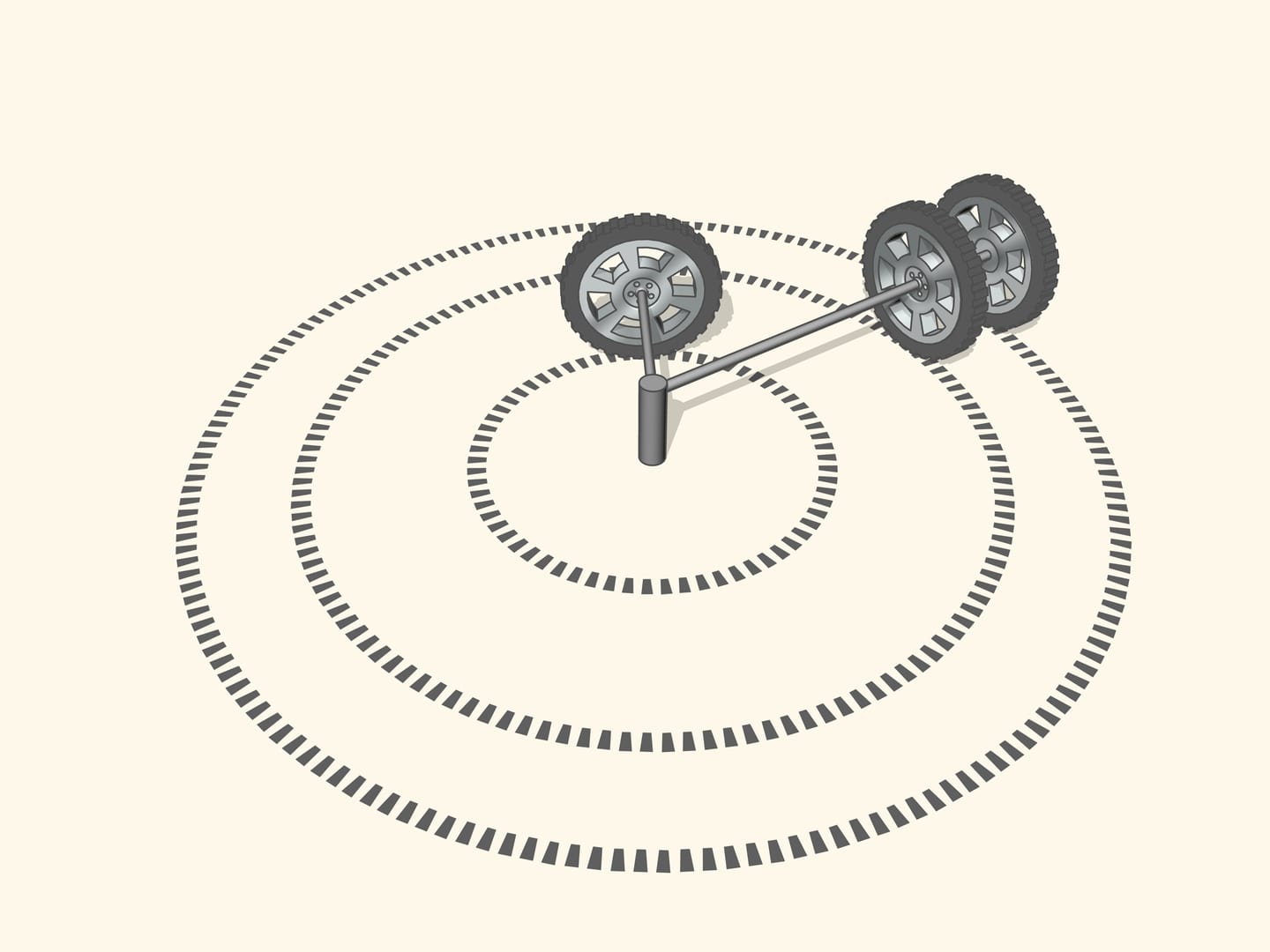
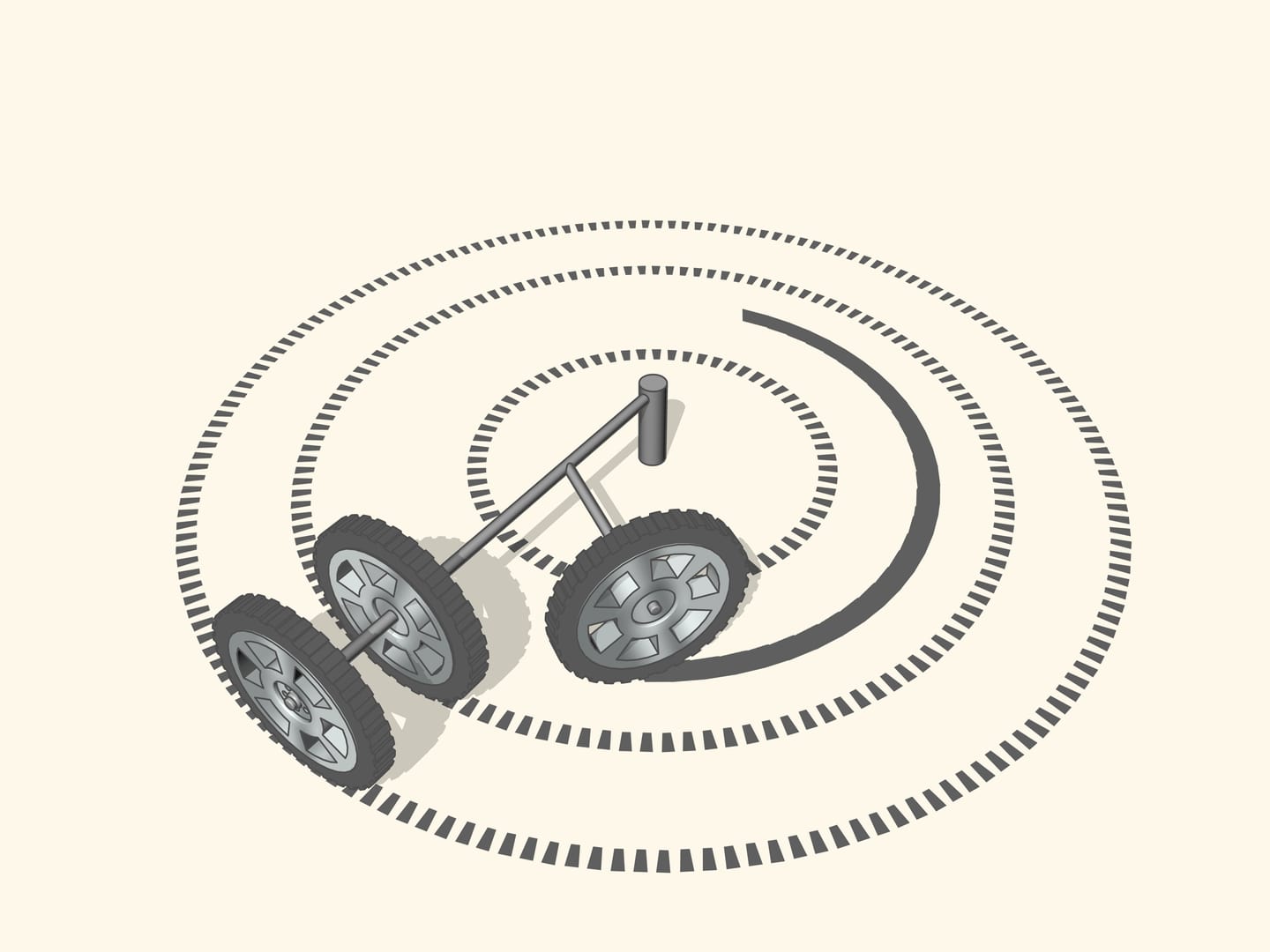
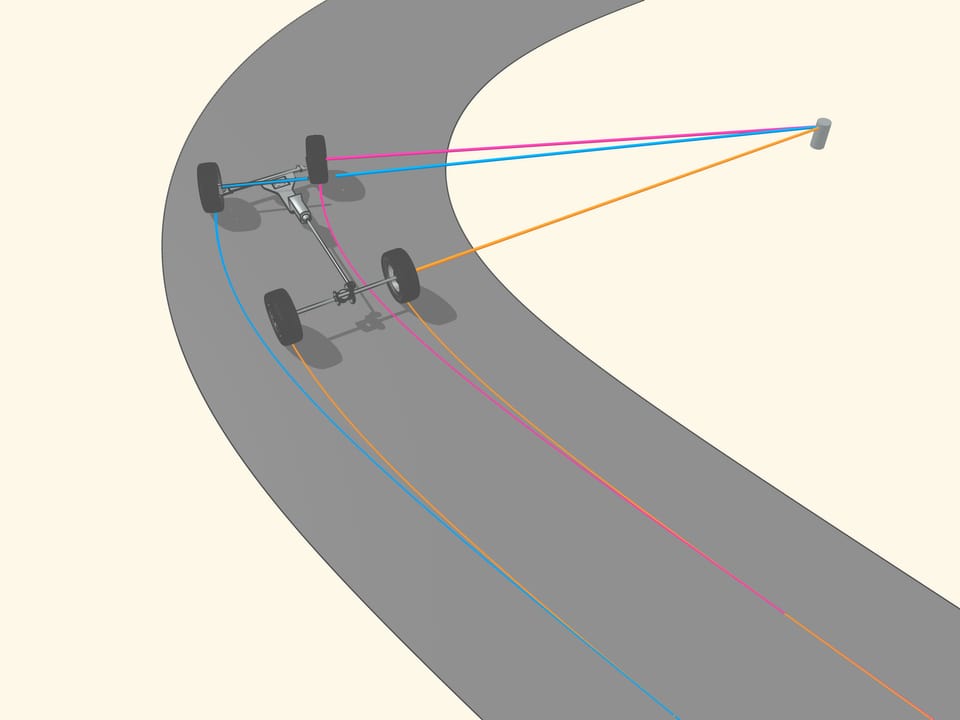
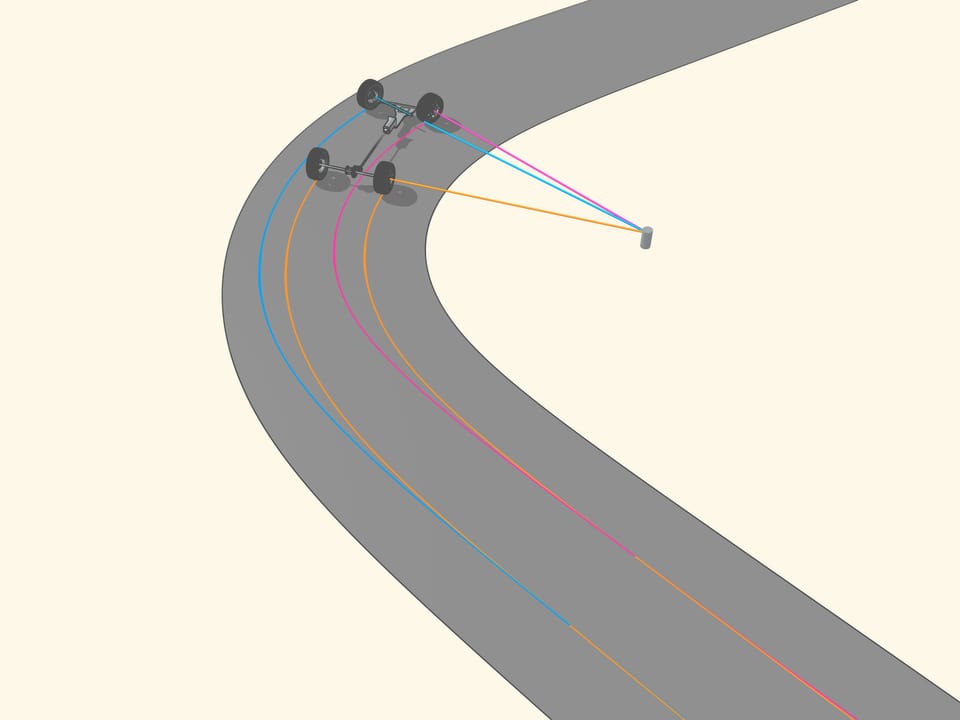
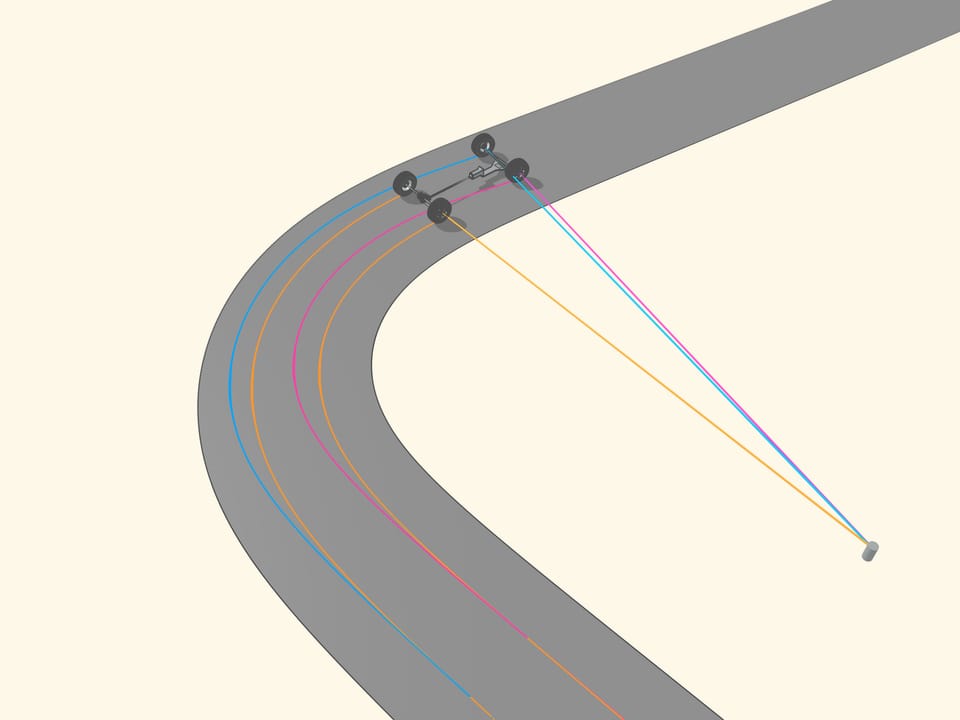
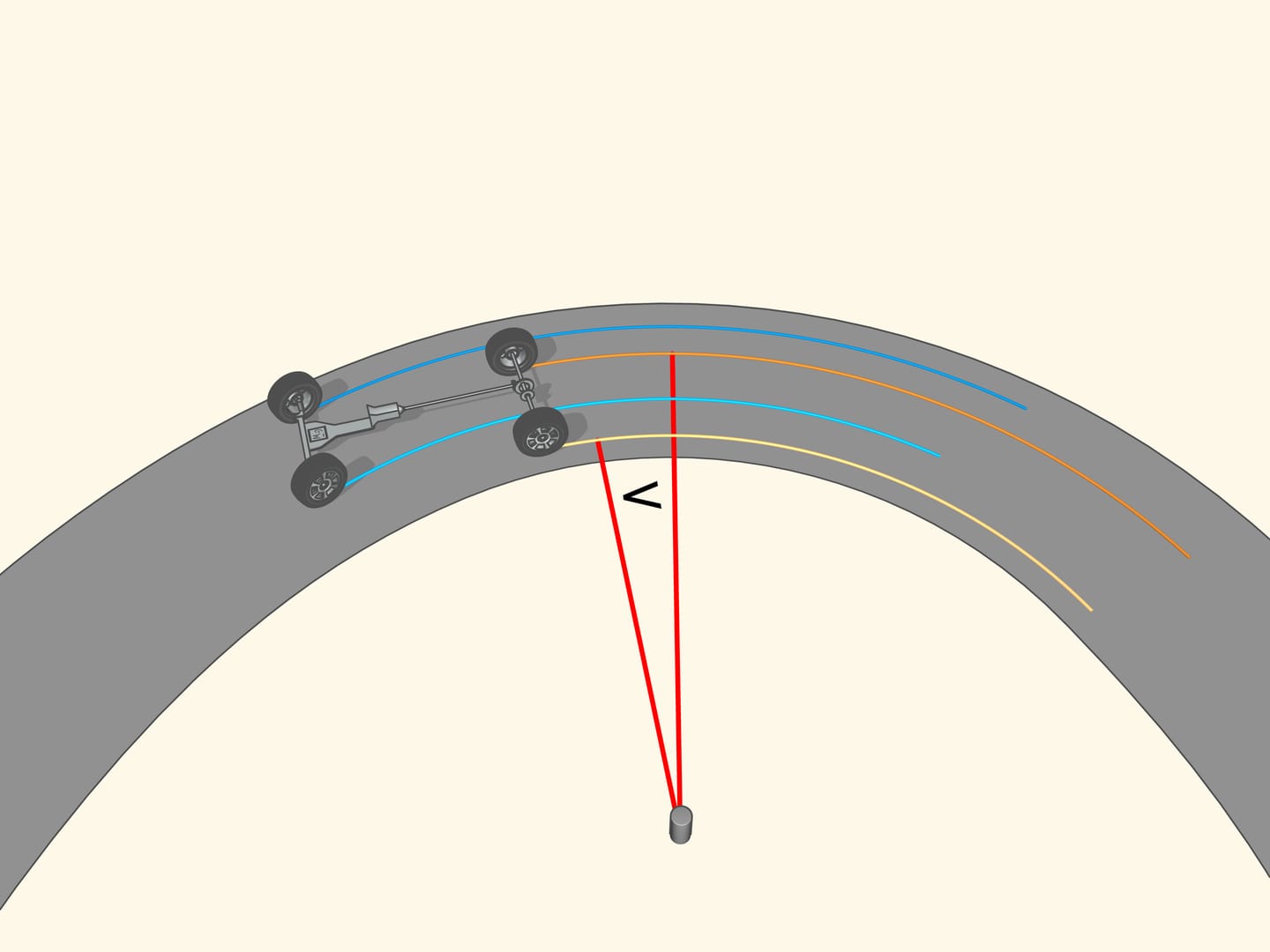
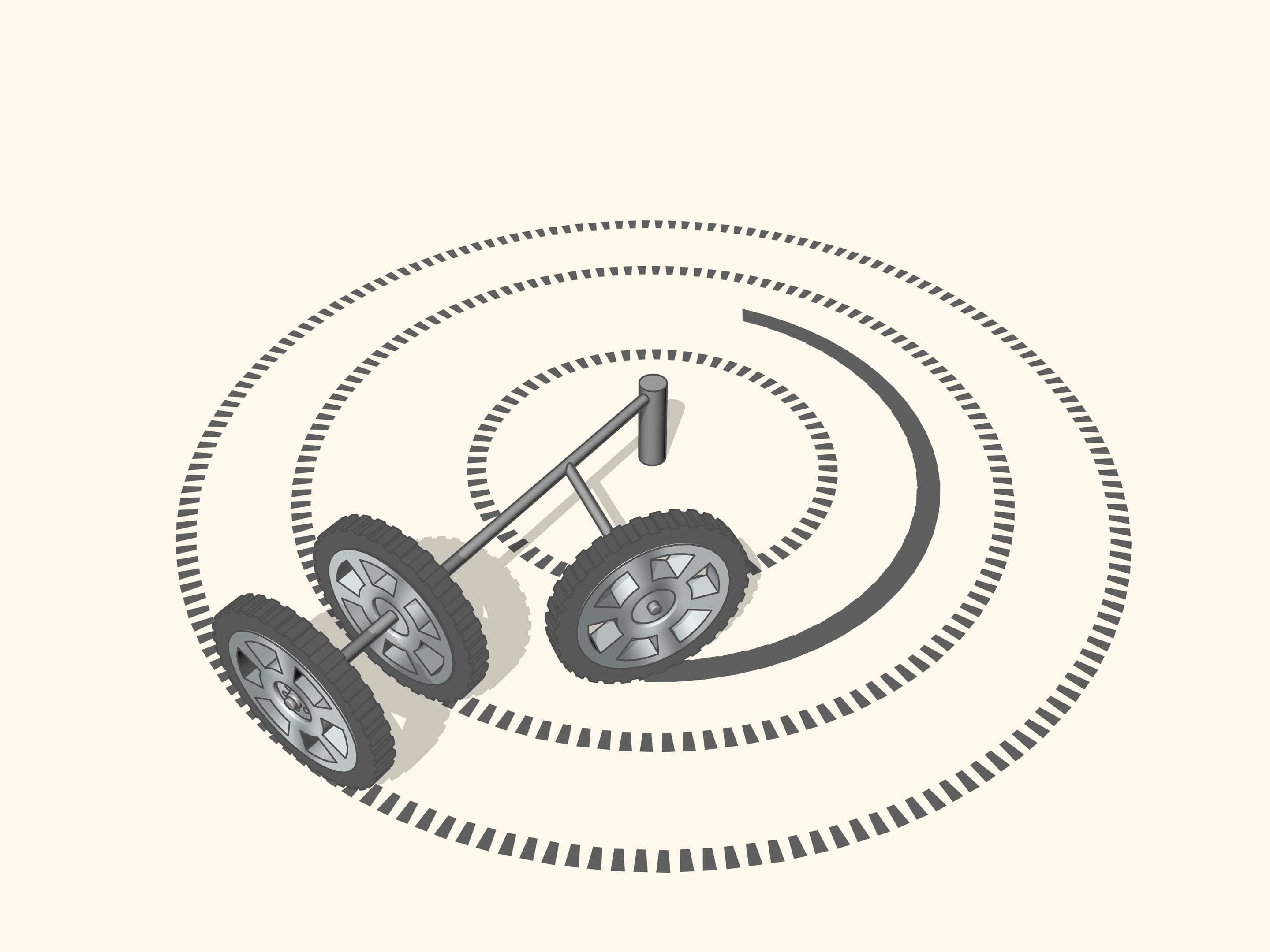
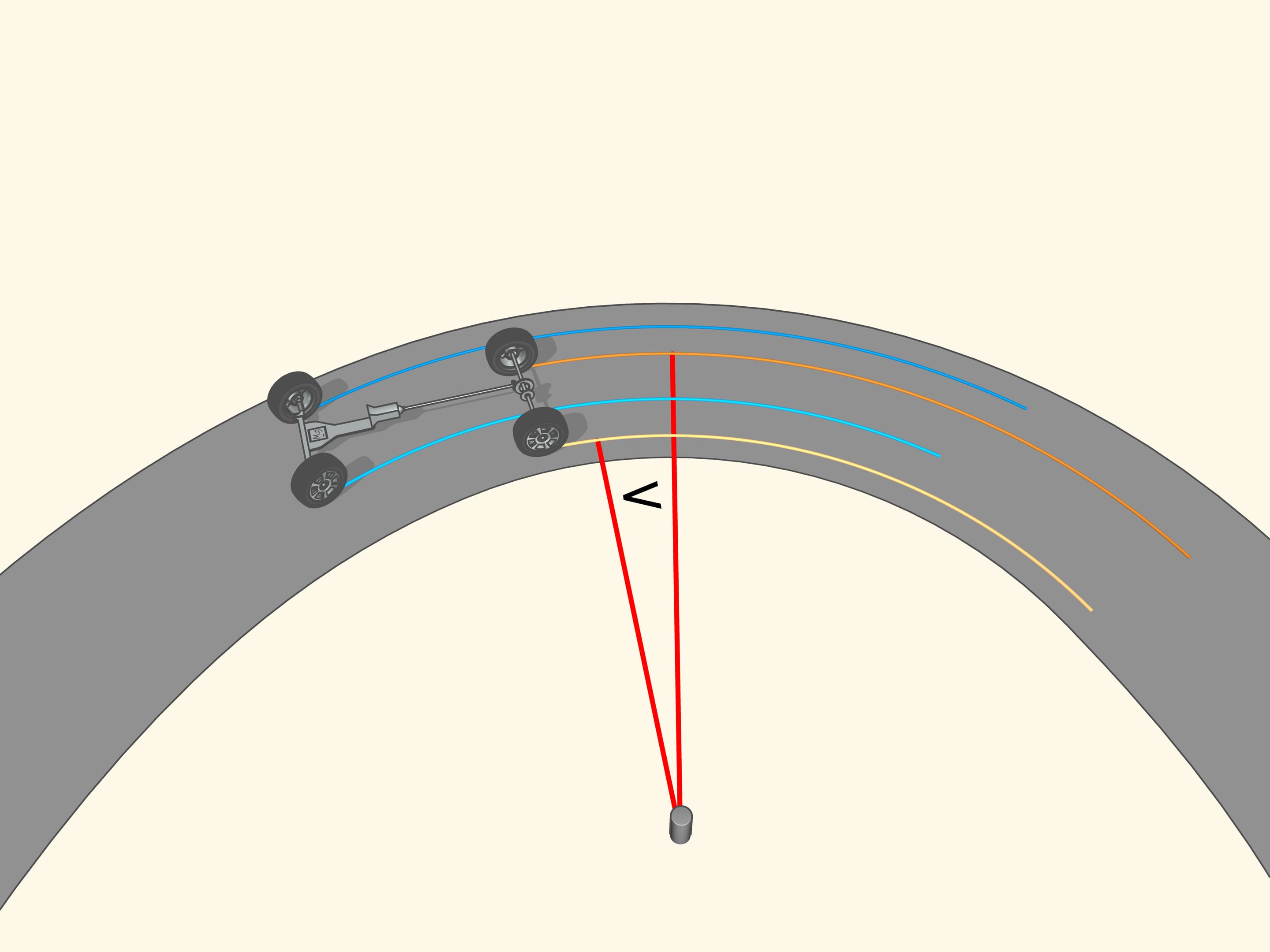
Si le prolongement de l’axe de la roue passe par le centre de rotation, la roue roule, en laissant une trace claire. Si le prolongement n’est pas dirigée vers le centre de rotation, la roue dérape pendant qu’elle tourne. Sa trace sera effacée par le glissement, et, surtout, le contrôle d’un véhicule avec des roues pareilles sera de plus en plus difficile quand la vitesse augmente. Ainsi, pour un bon contrôle, les prolongements des axes des roues doivent toutes être dirigées vers le centre de rotation. Mais qu’est–ce que cela signifie pour une voiture à quatre roues?
Pour commencer, nous observerons le braquage le long d’une courbe simple, c’est à dire un arc de cercle.
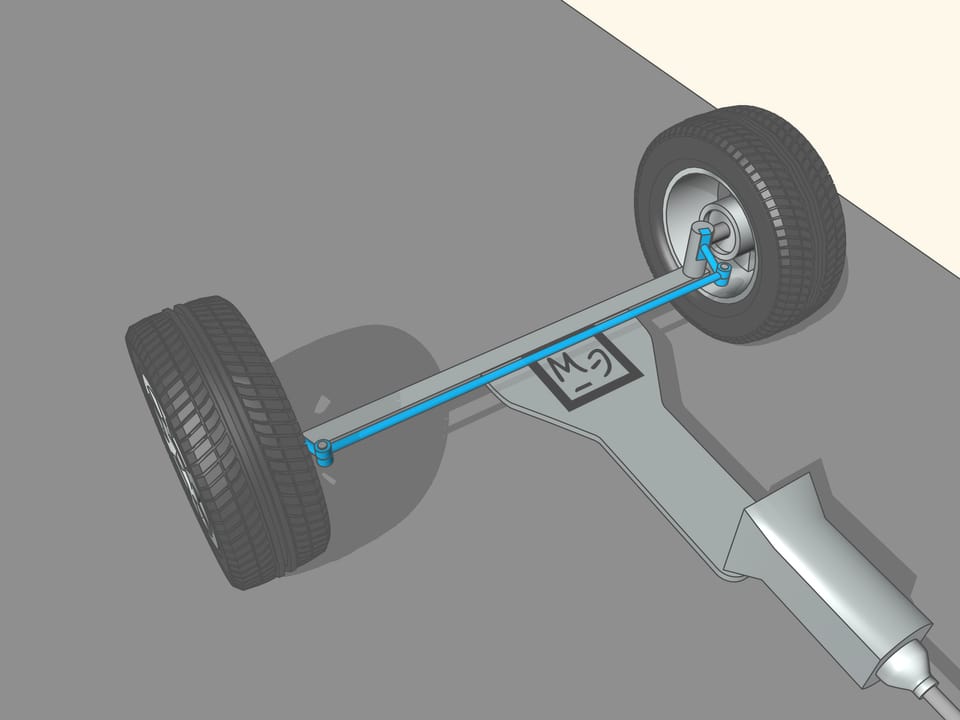
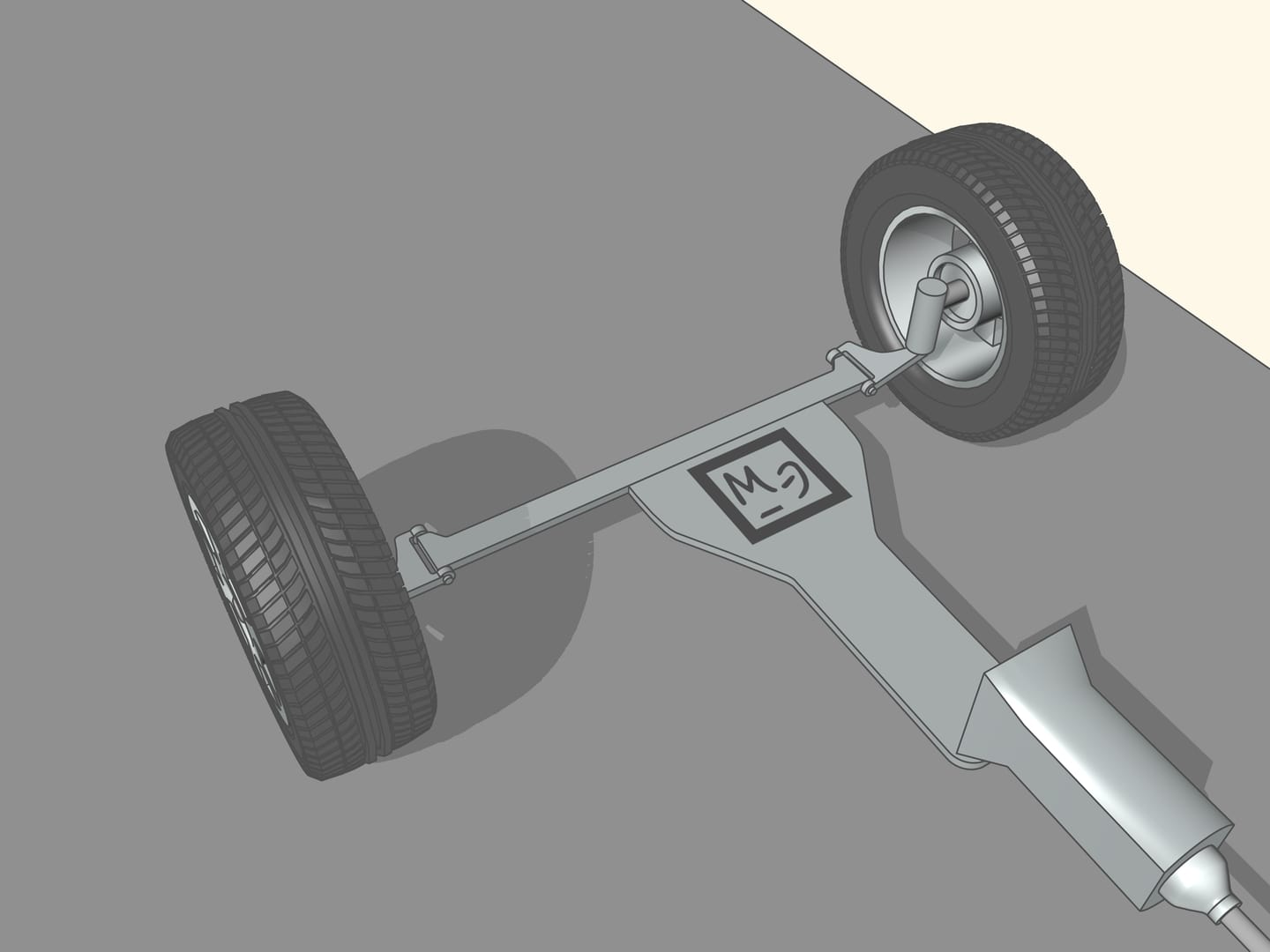
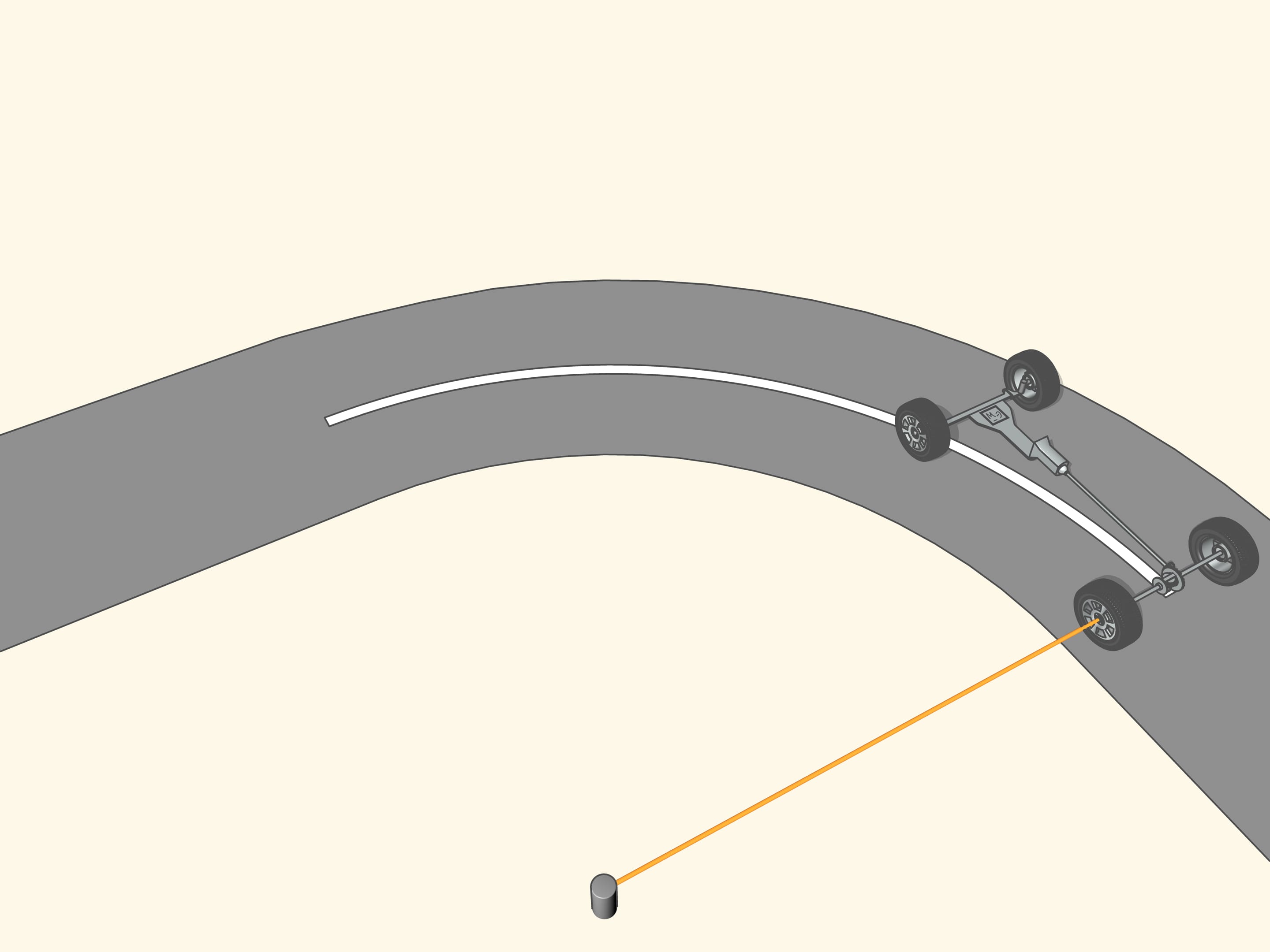
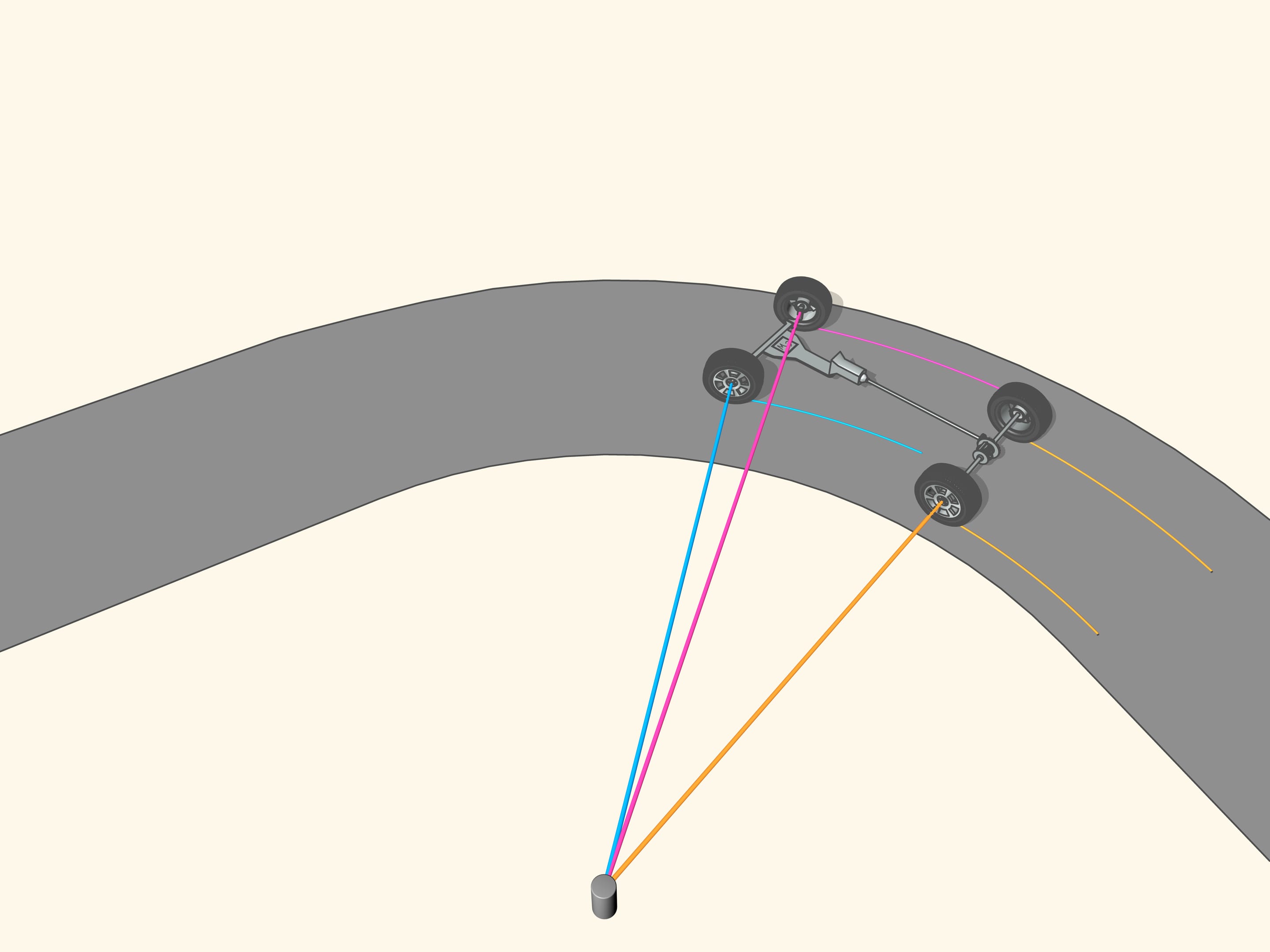
Puisque les roues arrière dans la plupart des voitures ont le même axe, le prolongement de cet axe doit être dirigé vers le centre de ce cercle. Les roues avant sont alors tourné de sorte que l’axe de chacune est dirigé vers le même centre. Cela signifie que pour un bon contrôle il faut être capable de tourner les roues avant d’angles différents, de sorte que ces roues ne seront pas parallèles!
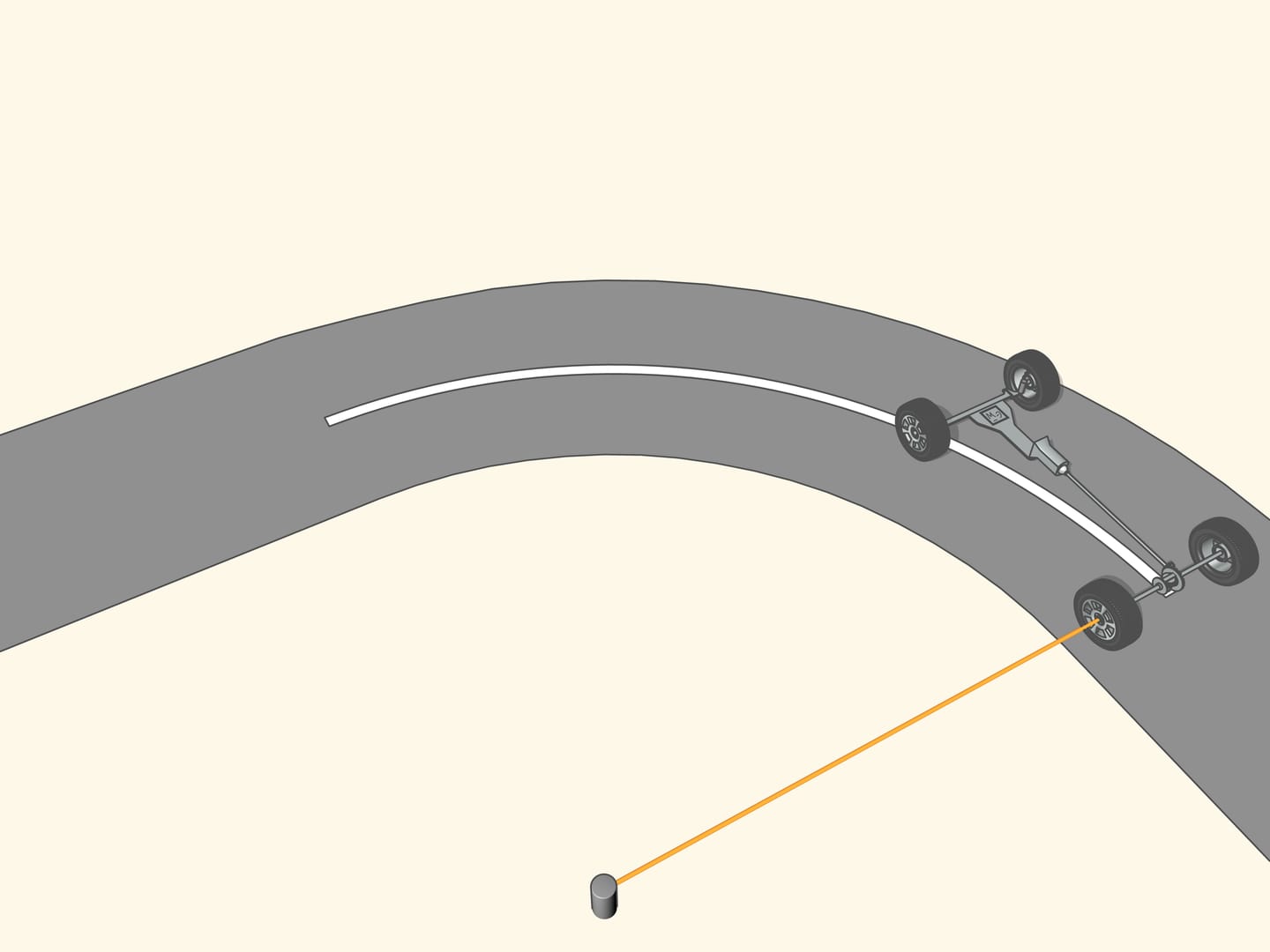
Vous direz que les courbes ne sont pas toujours des arcs de cercles, et en plus que la voiture ne s’arrête pas, quand on braque. Ceci, bien sûr, est vrai, mais il arrive que pendant un virage à chaque instant on peut considérer que la voiture voyage le long d’un arc de cercle dont le rayon et le centre dépendent de cet instant du temps.
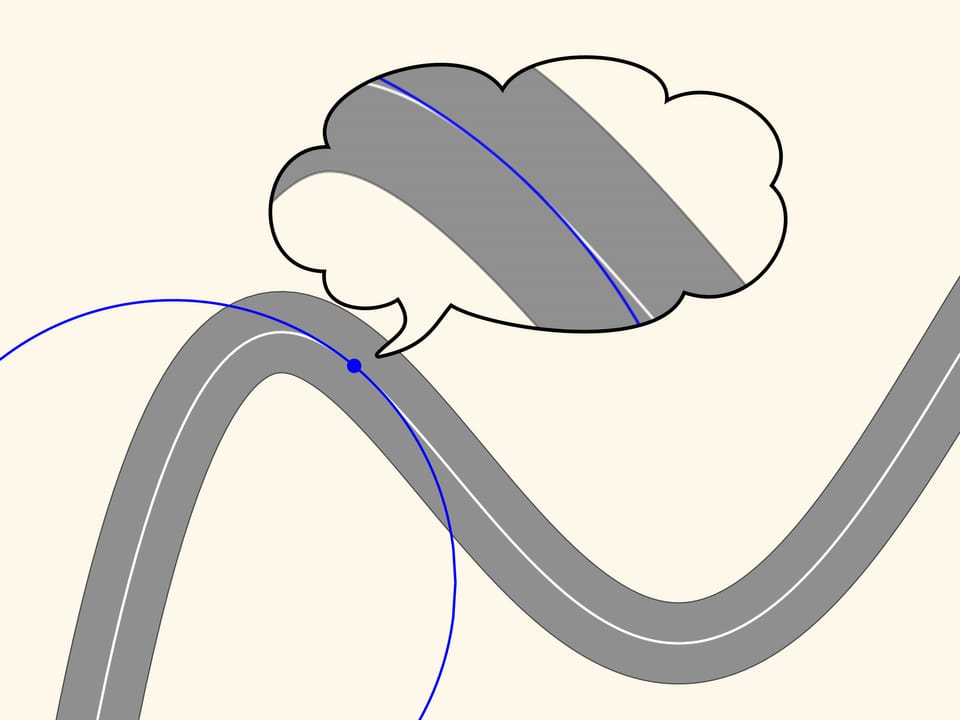
Considérons une rue quelconque. Afin d’être praticables en voiture, elle ne doit pas avoir des angles vifs, c’est–à–dire, la ligne du milieu sera, comme on dit en mathématiques, une courbe lisse.
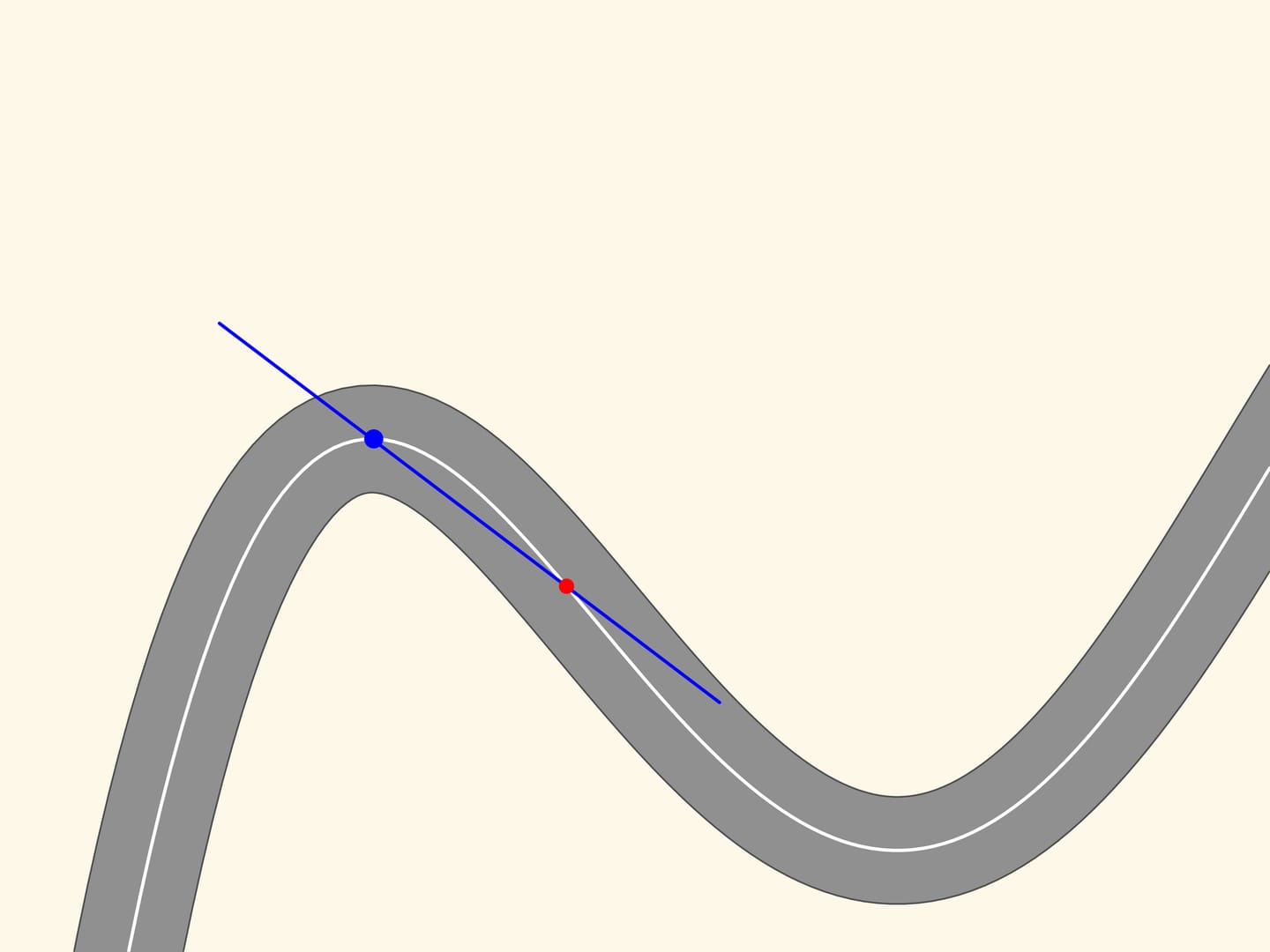
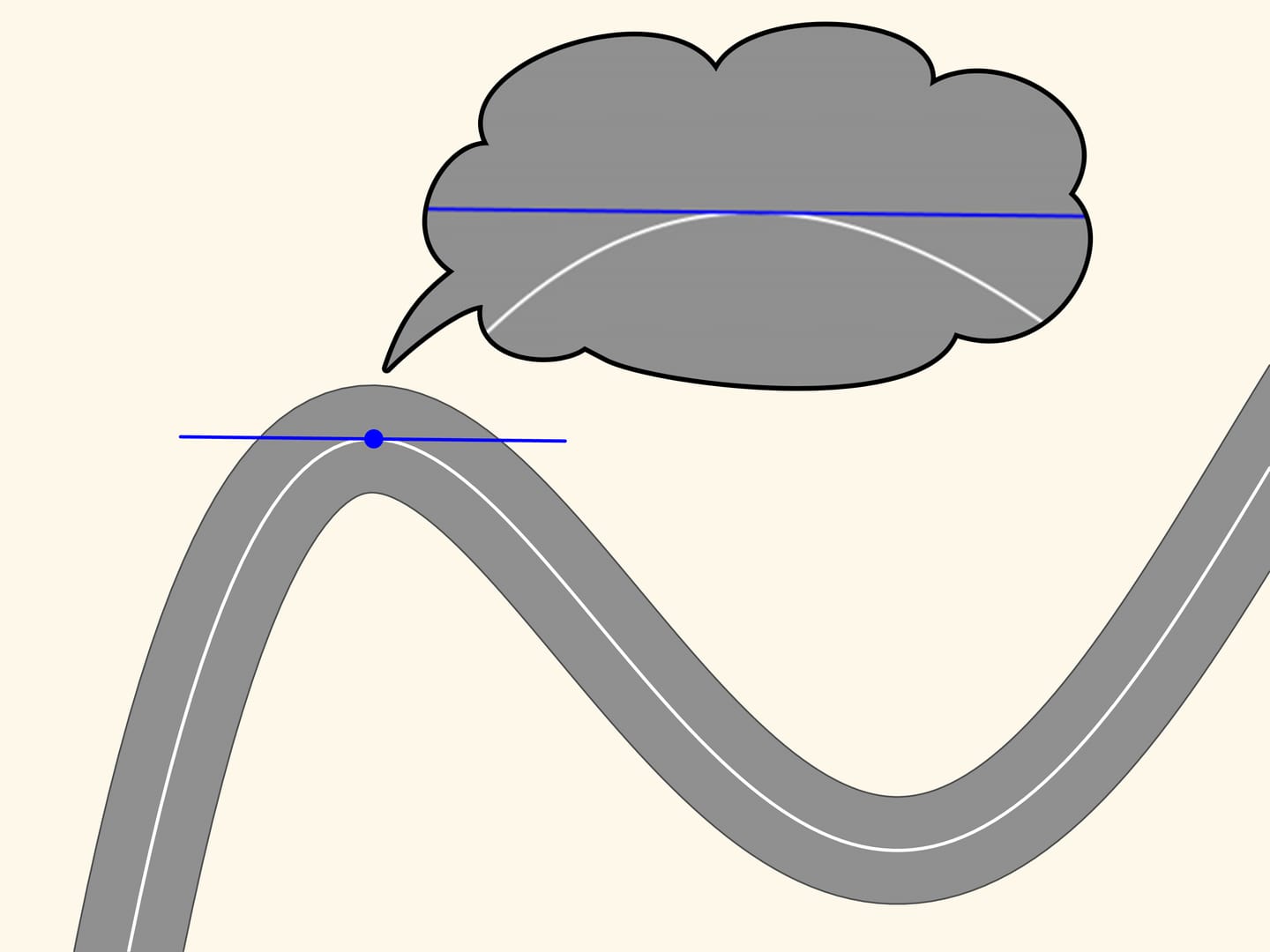
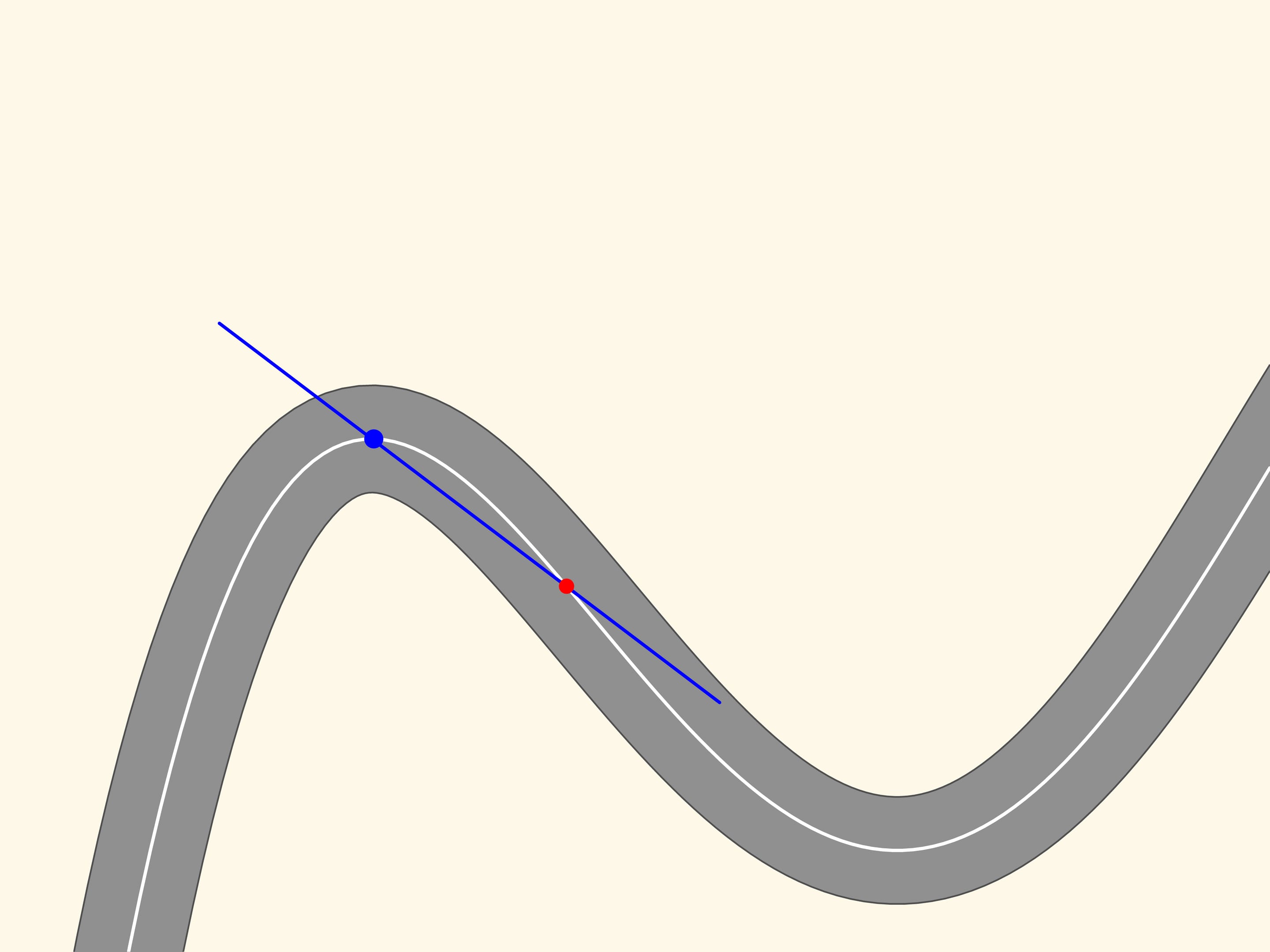
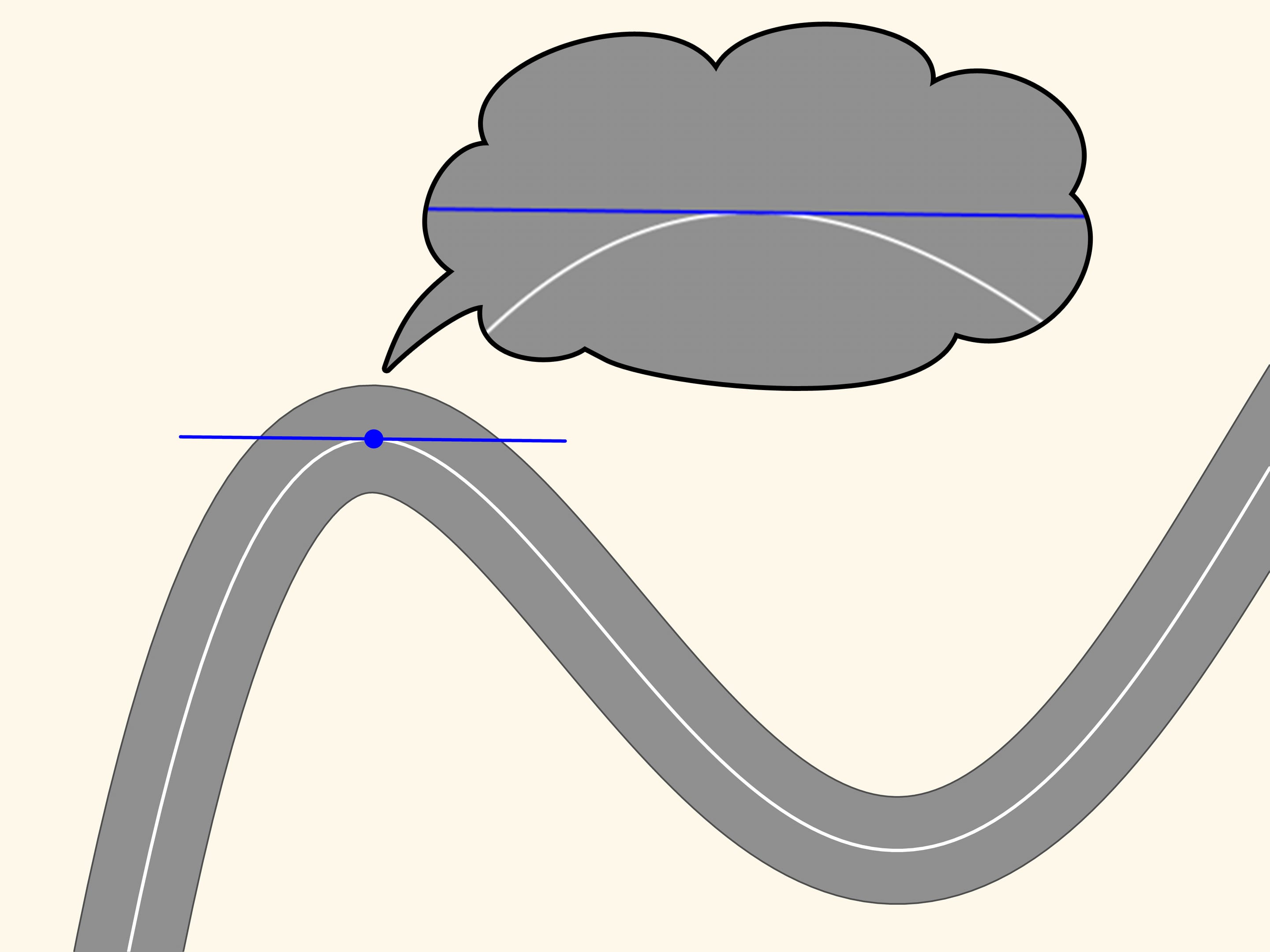
Prenons n’importe quel point sur cette ligne et marquons le en rouge, et un autre, un peu loin du premier, marqué en bleu. Ces deux points définissent sur le plan une seule ligne droite qui les relie, droite que nous allons tracer. Maintenant, déplaçons le point rouge le long de la courbe vers le point bleu. À l’instant où les points coïncident, la droite définie par eux deviendra la tangente. Elle représente l’approximation linéaire de la courbe dans un petit voisinage du point. Cependant nous observerons, en zoomant, que la courbe et la droite ne sont proches que pour un petit trait.
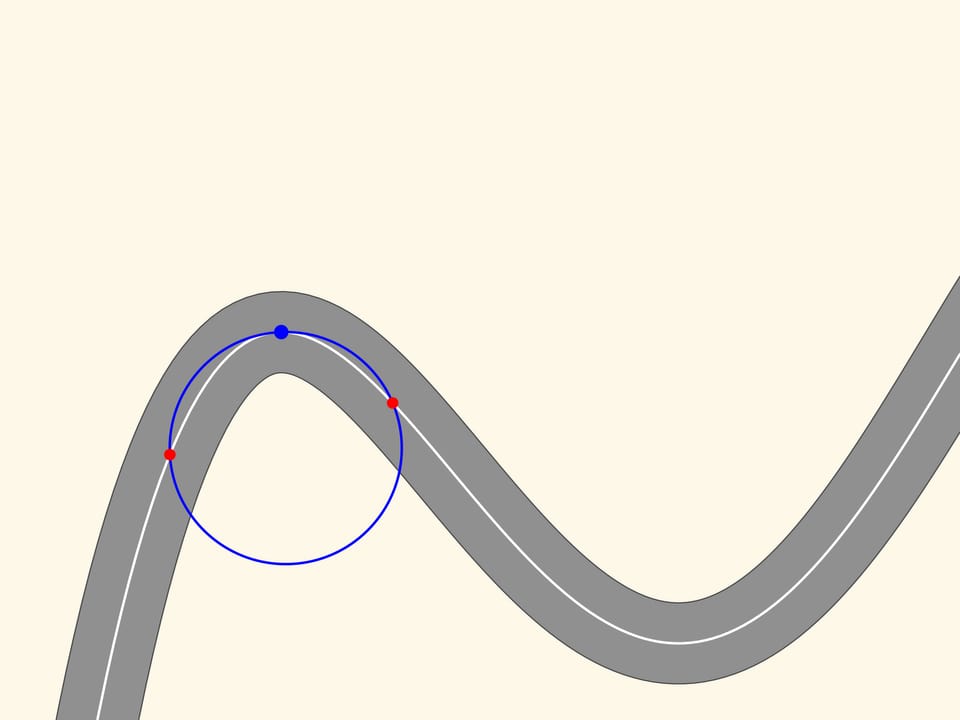
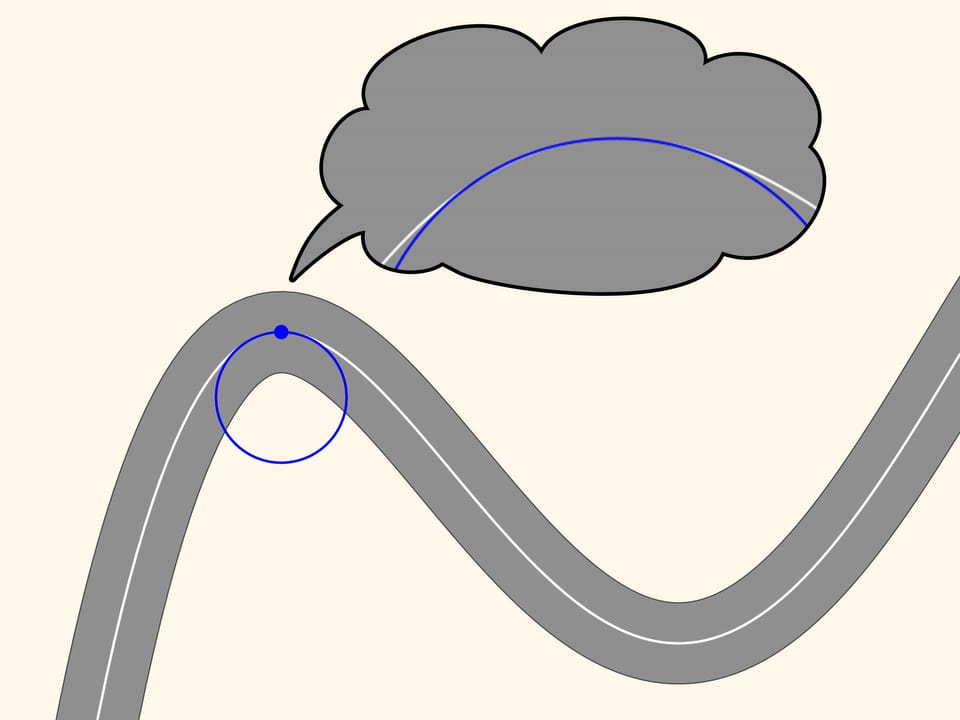
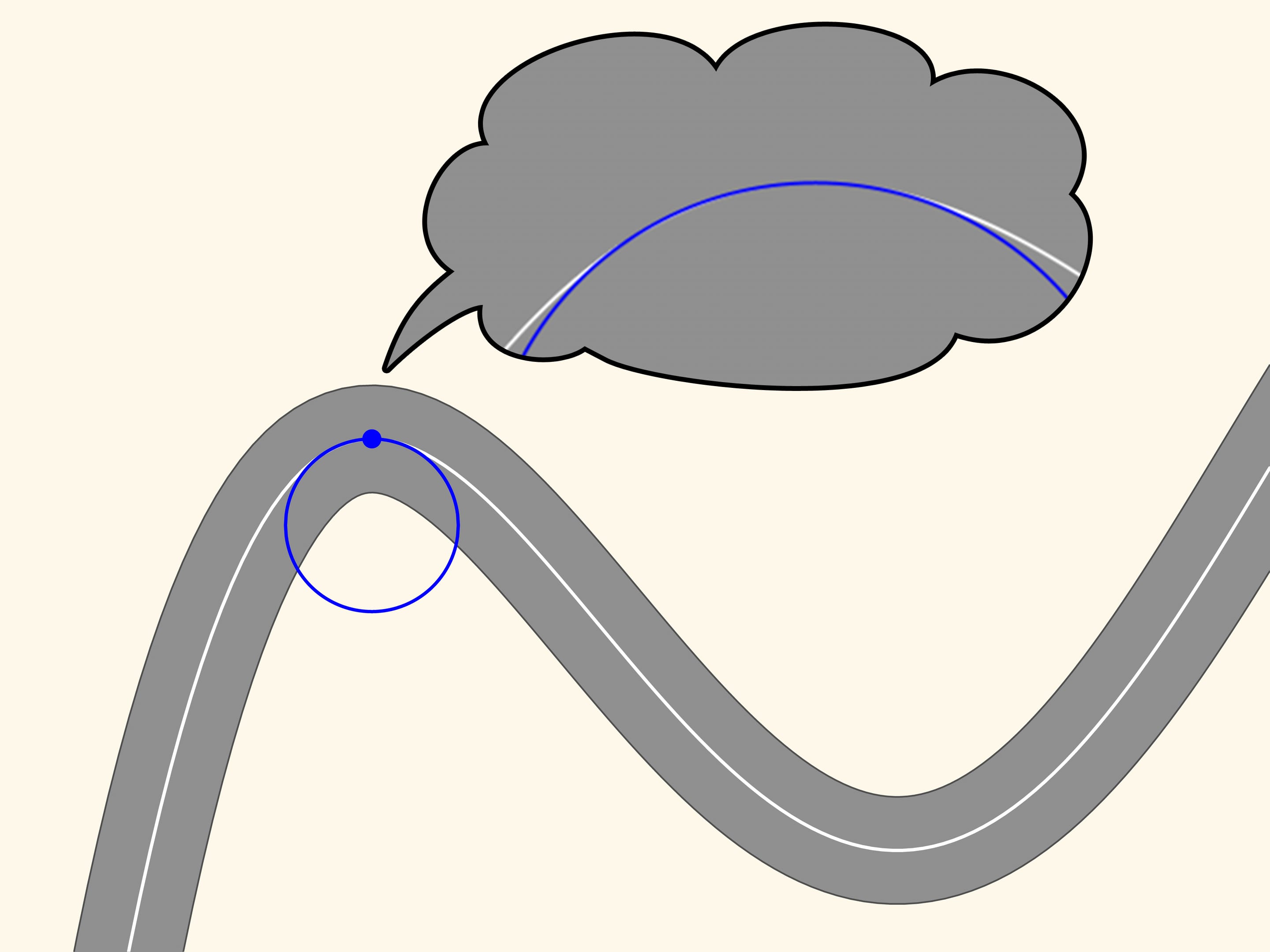
Prenons maintenant sur la courbe deux points rouges, un à droite et l’autre à gauche du point bleu. Trois points qui ne sont pas sur une ligne droite définissent un seul cercle, cercle que nous allons tracer. Maintenant, déplaçons les deux points rouges vers le point bleu. À l’instant où les trois points coïncident nous obtenons un cercle, qui est appelé osculateur. Il réalise l’approximation au second ordre de la courbe, et par le zoom on peut voir que cette approximation est meilleure. Nous observons que dans un morceau de courbe, le long du quel le rayon de courbure augmente ou diminue (comme dans les parties en montée et en descente de la courbe dans la figure), le cercle osculateur coupe toujours la courbe, contrairement à la tangente, qui est situé toujours dans la même partie du plan, par rapport à la courbe, dans un voisinage du point de tangence
Puisque dans notre cas le cercle osculateur donne une bonne approximation de notre courbe et peut être construit à chaque point, le mouvement le long d’une rue avec des courbes peut être considéré à chaque instant du temps comme le mouvement le long d’un arc de cercle. Le rayon et le centre de ce cercle dépendent, évidemment, d’où la voiture se trouve à cet instant.
De cette façon, en se déplaçant le long d’une certaine courbe, on peut considérer que à tout moment la voiture se déplace sur un petit arc de cercle. Et notre premier cas, où la rue même est un arc de cercle, est donc essentiel pour étudier tout virement.
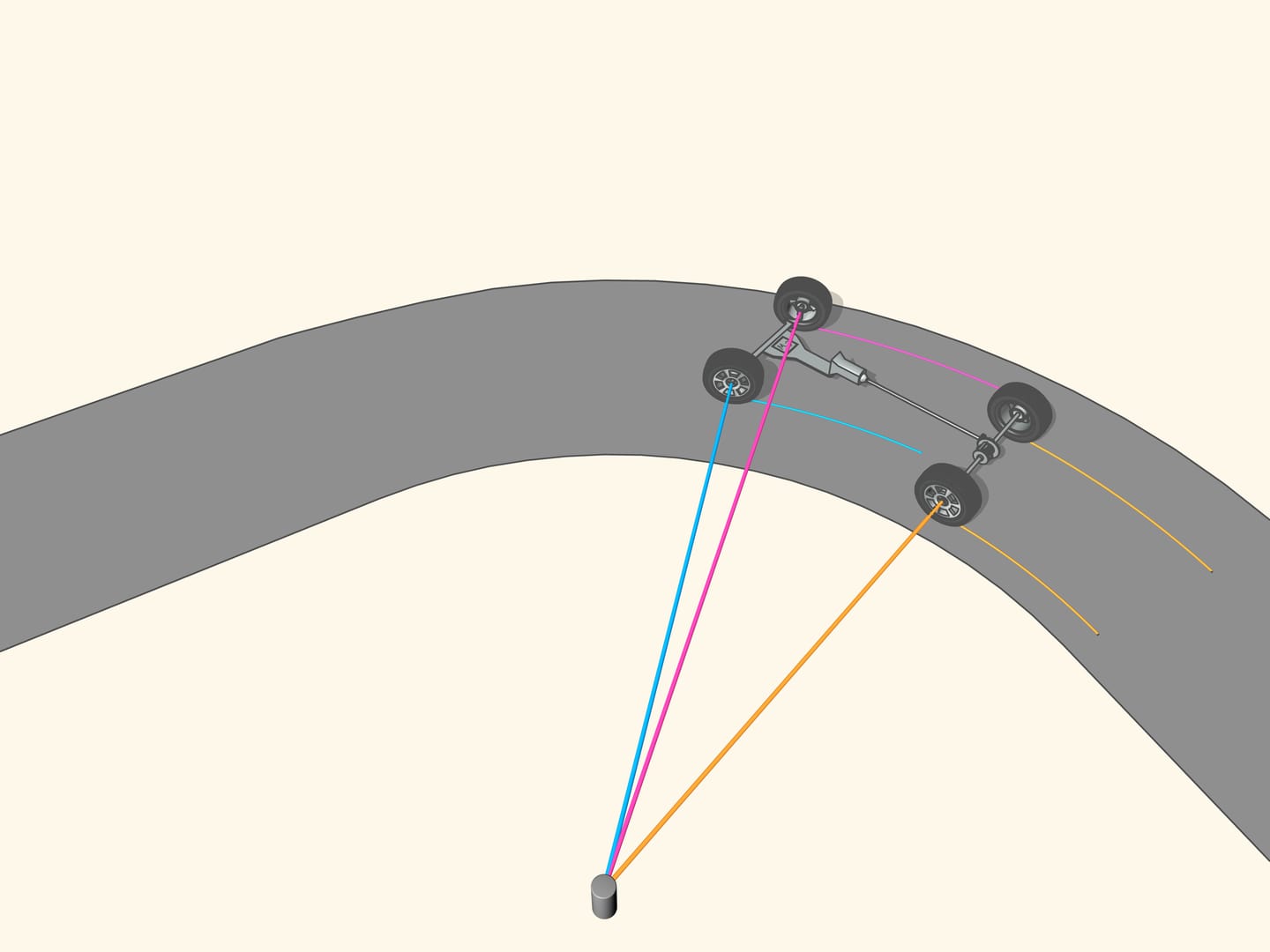
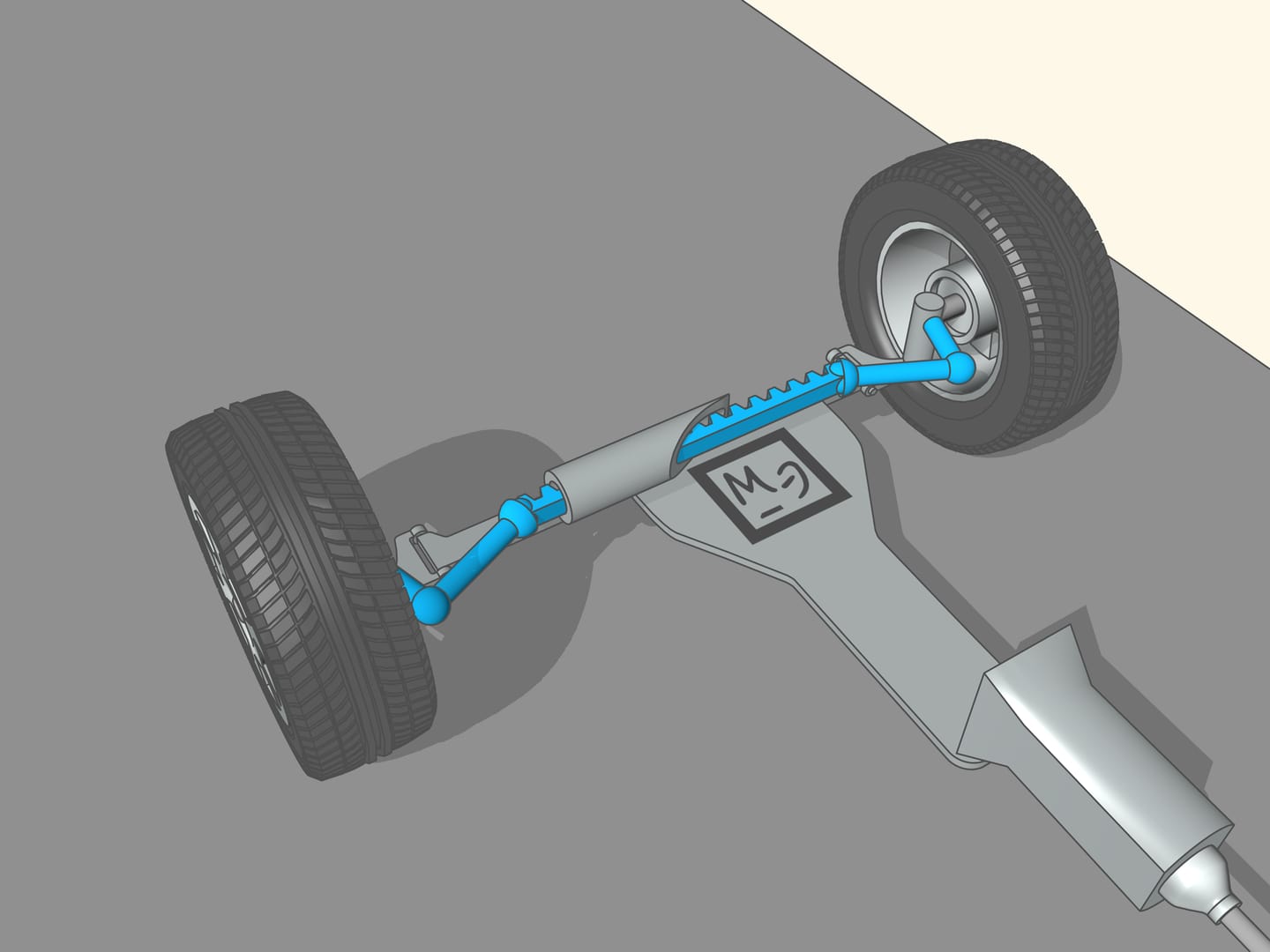
Mais comment obtenir que pour n’importe quelle position du volant, le prolongement de l’axe des roues est dirigée vers le centre instantané de courbure (c’est à dire le centre du cercle osculateur du point correspondant)?
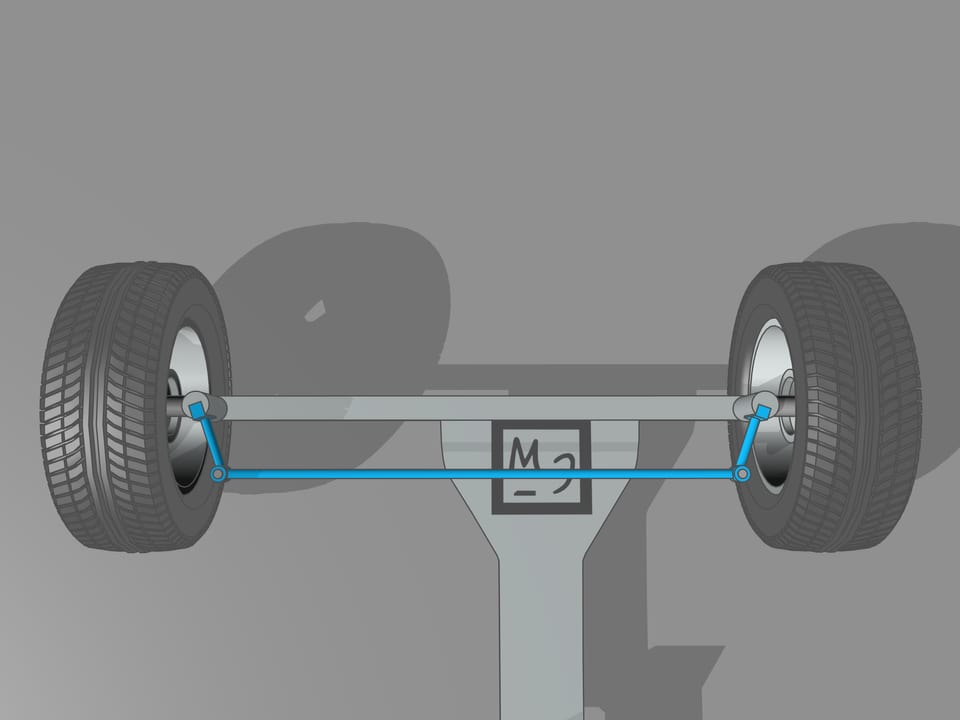
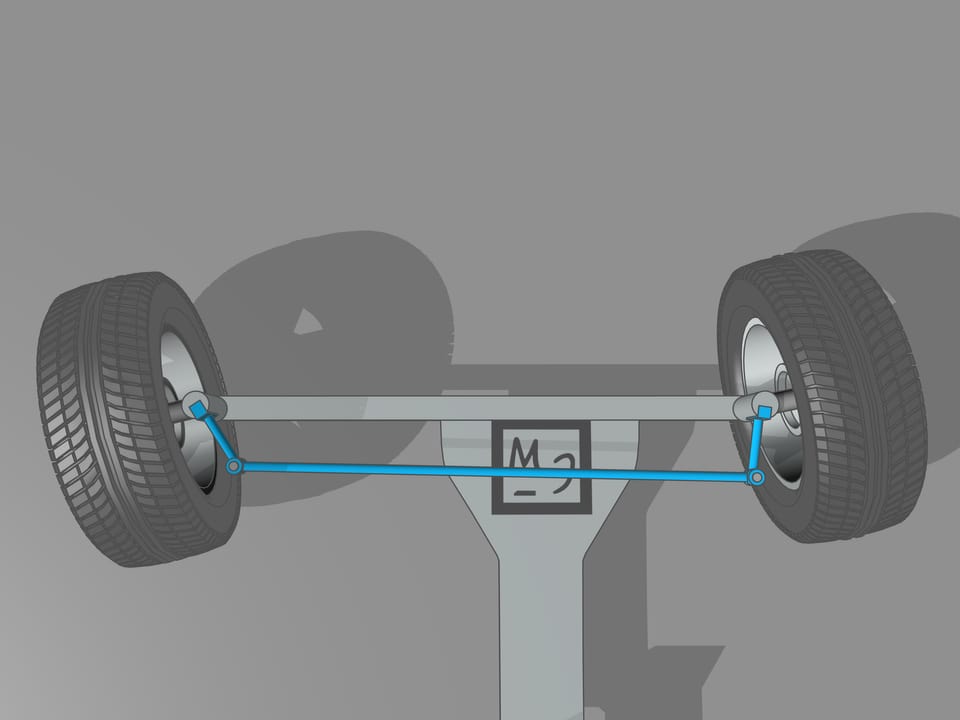
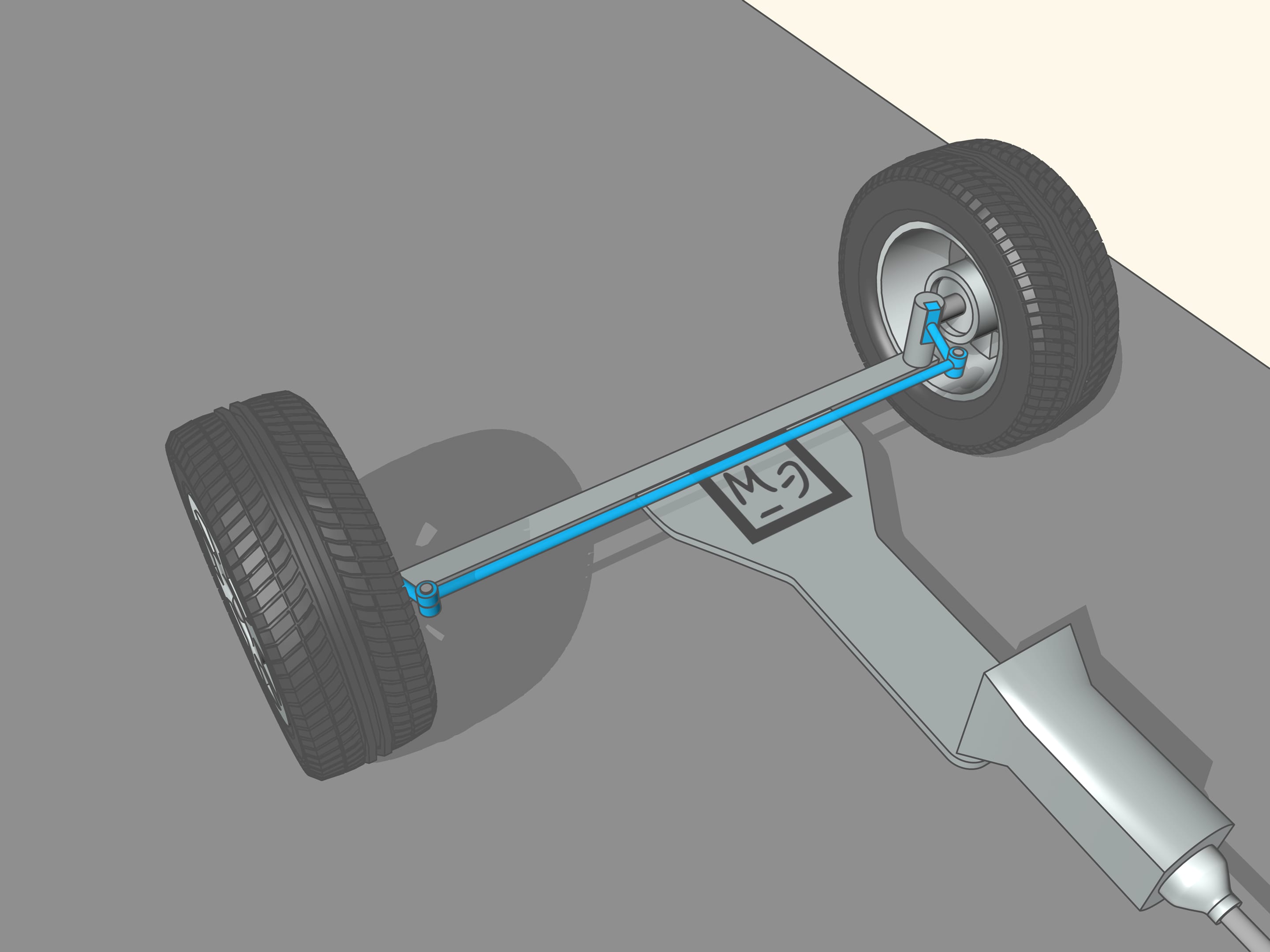
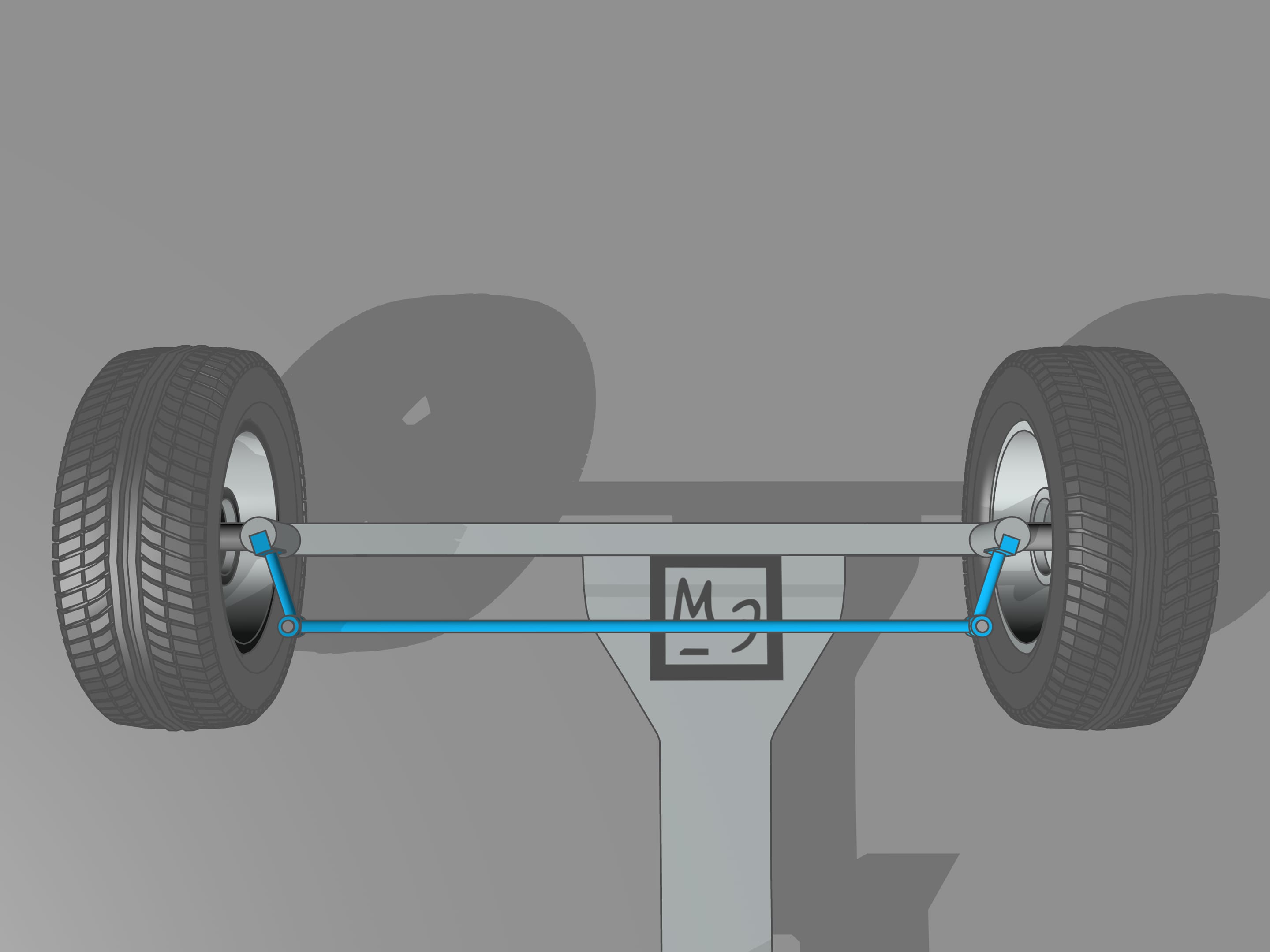
Il arrive que la géométrie vient ici à notre aide, et plus précisément avec le trapèze isocèle, que nous connaissons de l’école: un quadrilatère avec deux côtés parallèles, appelés bases, et deux autres côtés non parallèles égaux entre eux. En choisissant la bonne longueur des côtés du trapèze, on obtient les conditions nécessaires pour un contrôle optimal: les prolongements des axes des roues avant se coupent en un point qui se trouve sur le prolongement de l’axe des roues arrière. Et ce point est le centre instantané de courbure.
C’était un maître artisan français, Charles Jeantland, l’inventeur un tel système de contrôle des roues des chars. Mais pour les chars, qui se déplacent à faible vitesse, cette invention n’était pas si indispensable que pour les voitures, et a été oublié. Seulement après trois quarts de siècle, deux ingénieurs allemands, deux pères de l’automobile, à savoir Gottlieb Daimler et Wilhelm Friedrich Karl Michael Benz, retournèrent au trapèze de Jeantland pour la construction de leurs voitures. Daimler en 1889 obtint le brevet pour sa «méthode de contrôle indépendant des roues avant avec des rayons de courbure différents». Et en 1893 Benz obtint le brevet pour sa «construction d’un système de contrôle avec des cercles tangents aux roues». Après avoir résolu le problème du contrôle des roues avant et d’autres questions techniques importantes, Karl Benz construit sa célèbre voiture à quatre roues indépendantes «Viktoria».
Du point de vue mathématique, le trapèze ne permet pas de créer les conditions nécessaires pour assurer que les prolongements des axes des roues avant se coupent toujours en un point sur le prolongement de l’axe des roues arrière. En utilisant du trapèze, ce point sera toujours un peu déplacé par rapport è la droite de l’axe arrière. Mais pourquoi avons–nous si longtemps parlé du trapèze, demandez–vous. On s’est préoccupé trop tôt: tout simplement, il ne faut pas appliquer la rigueur mathématique à des problèmes techniques, sans utiliser le sens commun. Pour que les prolongements des axes des roues avant se coupent toujours en un point sur le prolongement de l’axe des roues arrière est nécessaire que la longueur de la base plus petite du trapèze changes un peu. Pour la longueur usuelle de cette base, qui est plus d’un mètre, les changements nécessaires seraient au plus d’un centimètre, ce qui est inférieur au interstices entre les joints et à la tolérance de la fabrication.
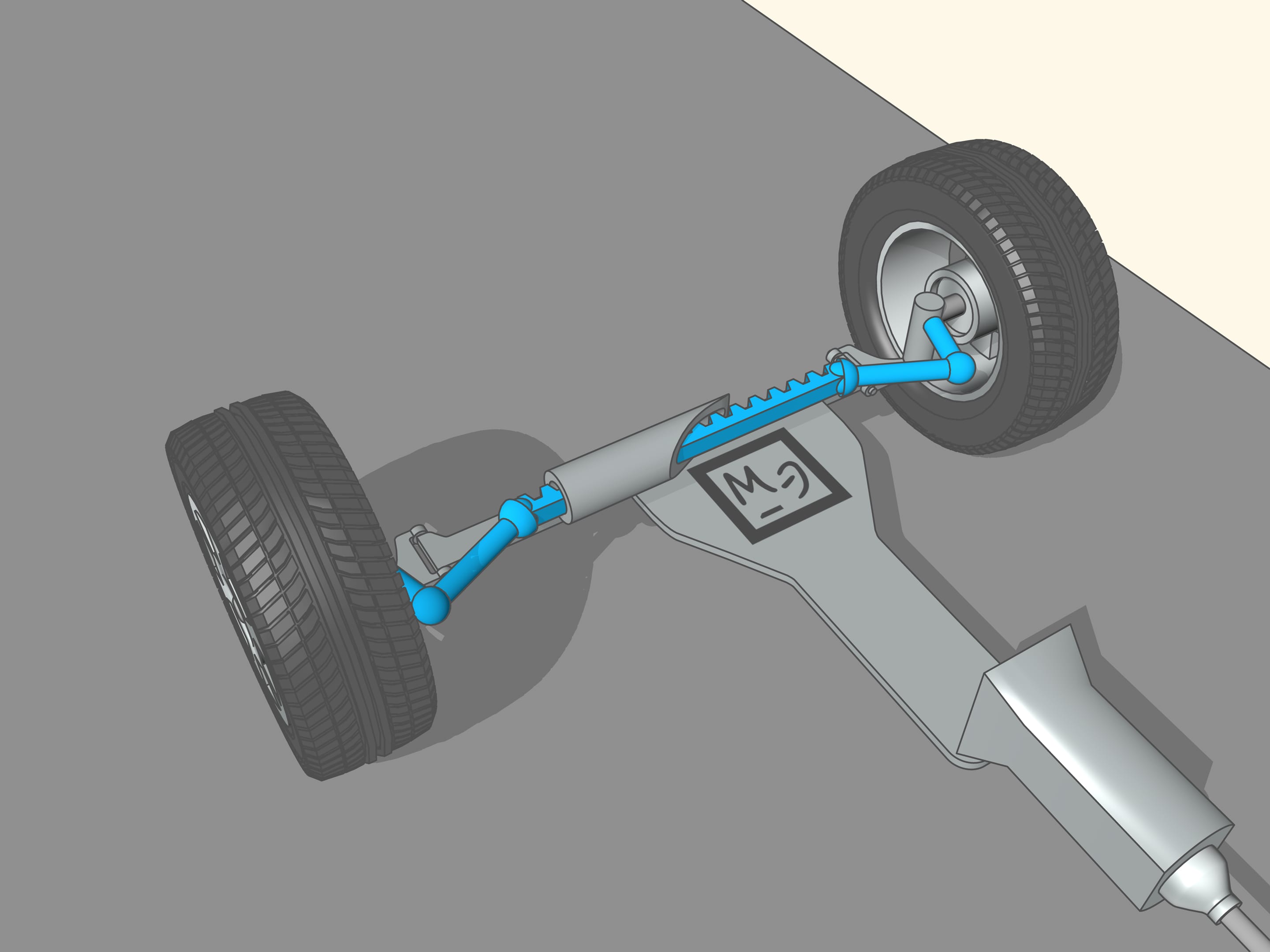
Depuis l’époque de la création des premières voitures, leur vitesse est augmentée considérablement. Ainsi le besoin d’un meilleur contrôle des roues avant a également augmenté. En outre, le trapèze est une figure plane géométriques. Cette méthode de contrôle des roues avant peut être utilisé uniquement avec suspensions de devant non indépendantes, c’est à dire lorsque les roues sont solidaires les unes aux autres et la droite joignant leurs centres est toujours parallèle au plan du trapèze. Maintenant, ce système peut être trouvé dans les camions. Dans les voitures modernes les suspensions des roues sont indépendantes, elle peuvent se déplacer verticalement l’une par rapport à l’autre. Pour contrôler le braquage on utilise des mécanismes plus complexes, qui ne sont plus planaires, souvent avec un élément central à forme de crémaillère. Même dans ce cas, calculer les éléments différents c’est un problème pour les mathématiciens et les ingénieurs. Mais historiquement, ces mécanismes continuent à être appelés «trapèzes du braquage».
En ce qui concerne le braquage de la voiture il y a encore une autre question, liée à la géométrie. La longueur d’un cercle de rayon R est égal, vous vous souviendrez, à 2πR, et la longueur d’un arc d’amplitude α est égale à αR. Lorsque la voiture se déplace le long d’un arc de cercle, la roue avant à l’extérieur, qui est plus éloigné du centre de courbure, se déplace le long d’un arc de rayon plus grand de celle à l’intérieur. Le même vaut pour les roues arrière: la roue extérieure décrit un arc de longueur supérieure que celui de la roue intérieure. Et puisque les rayons sont différents, ainsi les longueurs des chemins des roues du même axe doivent être différents. Dans le cas contraire l’une des deux roues déraperait, ce qui diminuerait le contrôle de la voiture.
Dans le cas où l’axe des roues n’est pas le principal, c’est à dire, les roues ne font pas bouger le véhicule – dans notre cas, les roues avant — c’est simple: chaque roue tourne avec sa vitesse nécessaire pour parcourir la courbe sans déraper.
Mais comment faire, de sorte que les roues de l’axe principale — dans notre cas, les roues arrière — soit poussent constamment la voiture, soit tournent à des vitesses différentes?
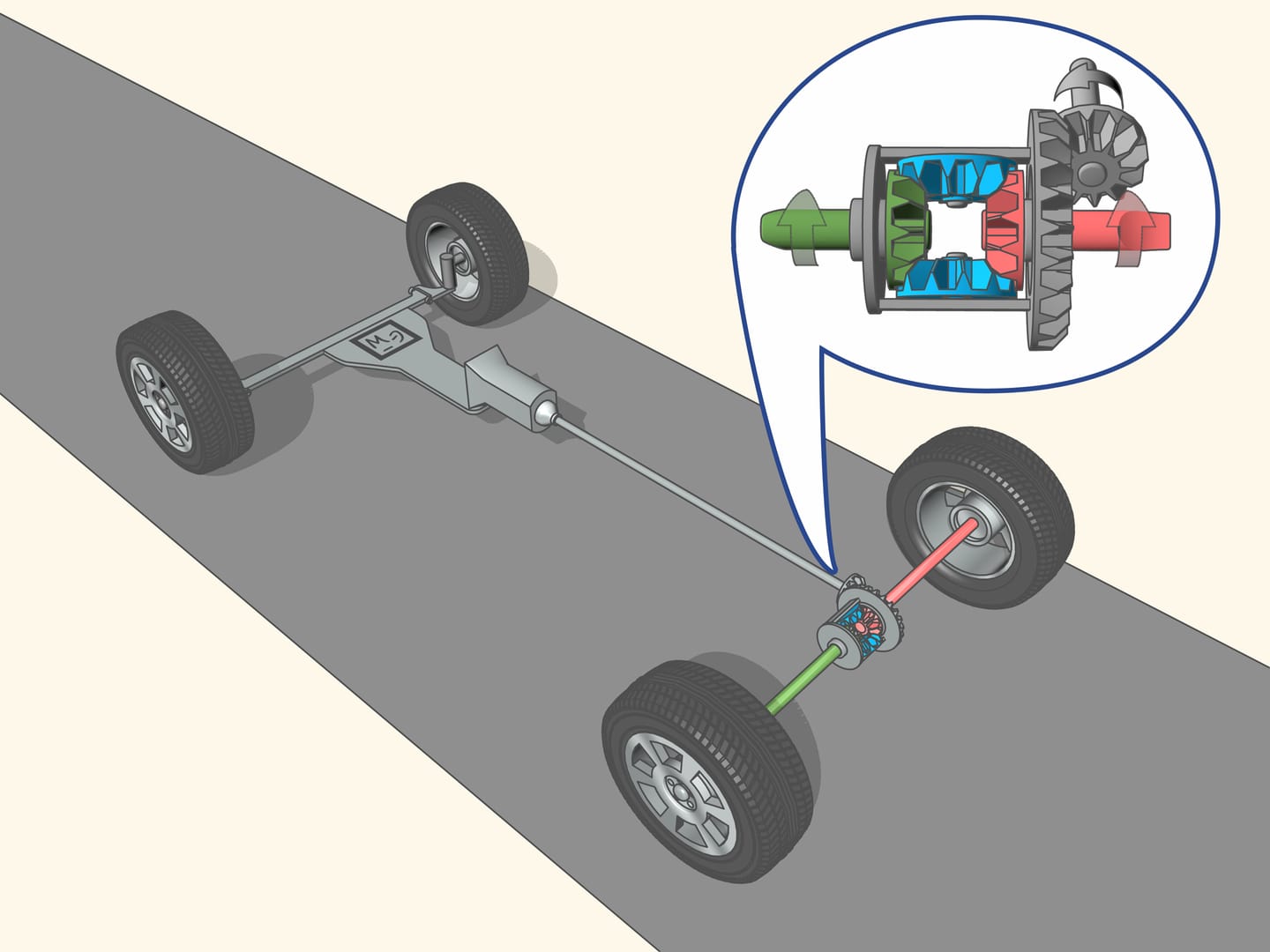
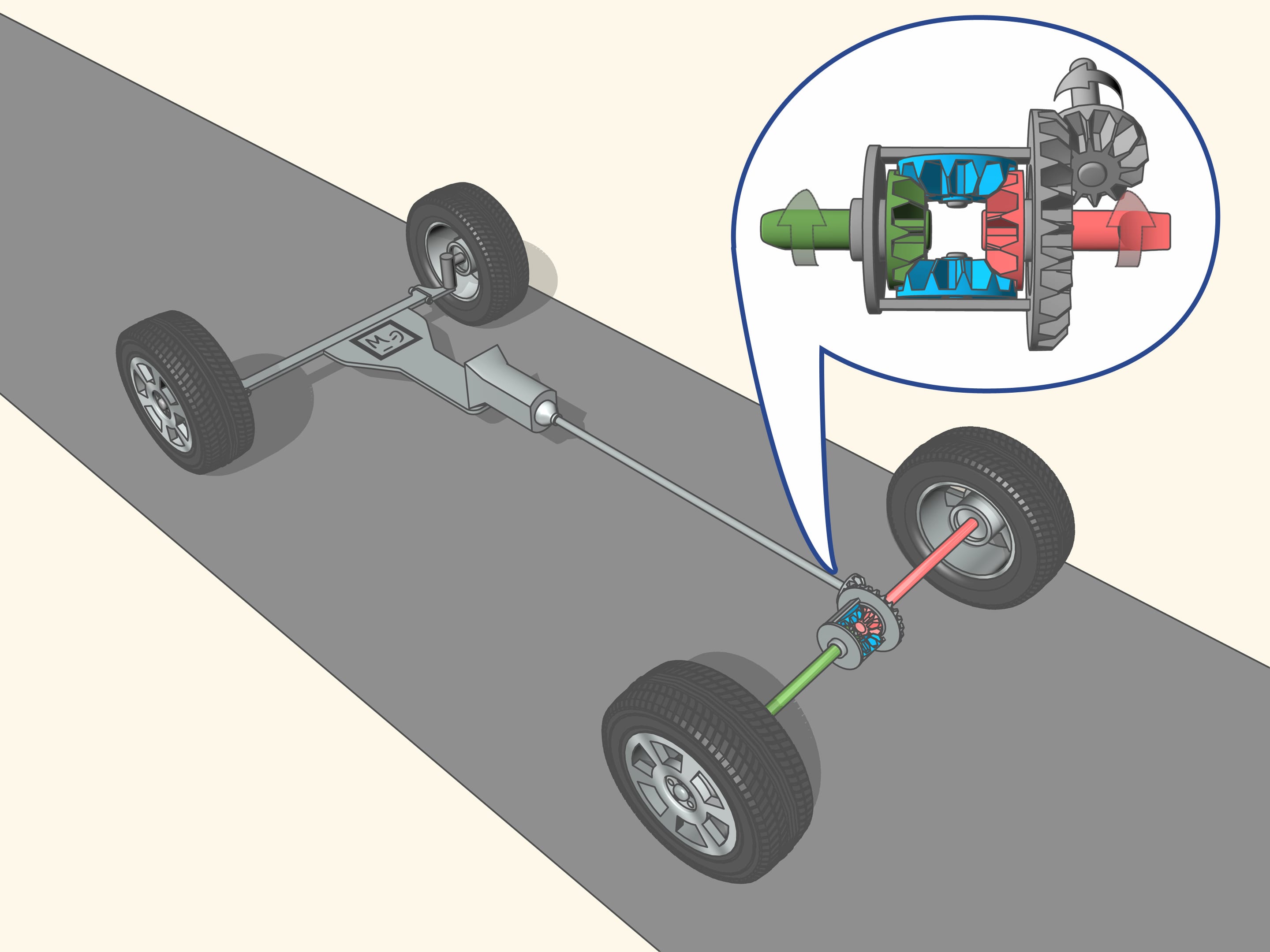
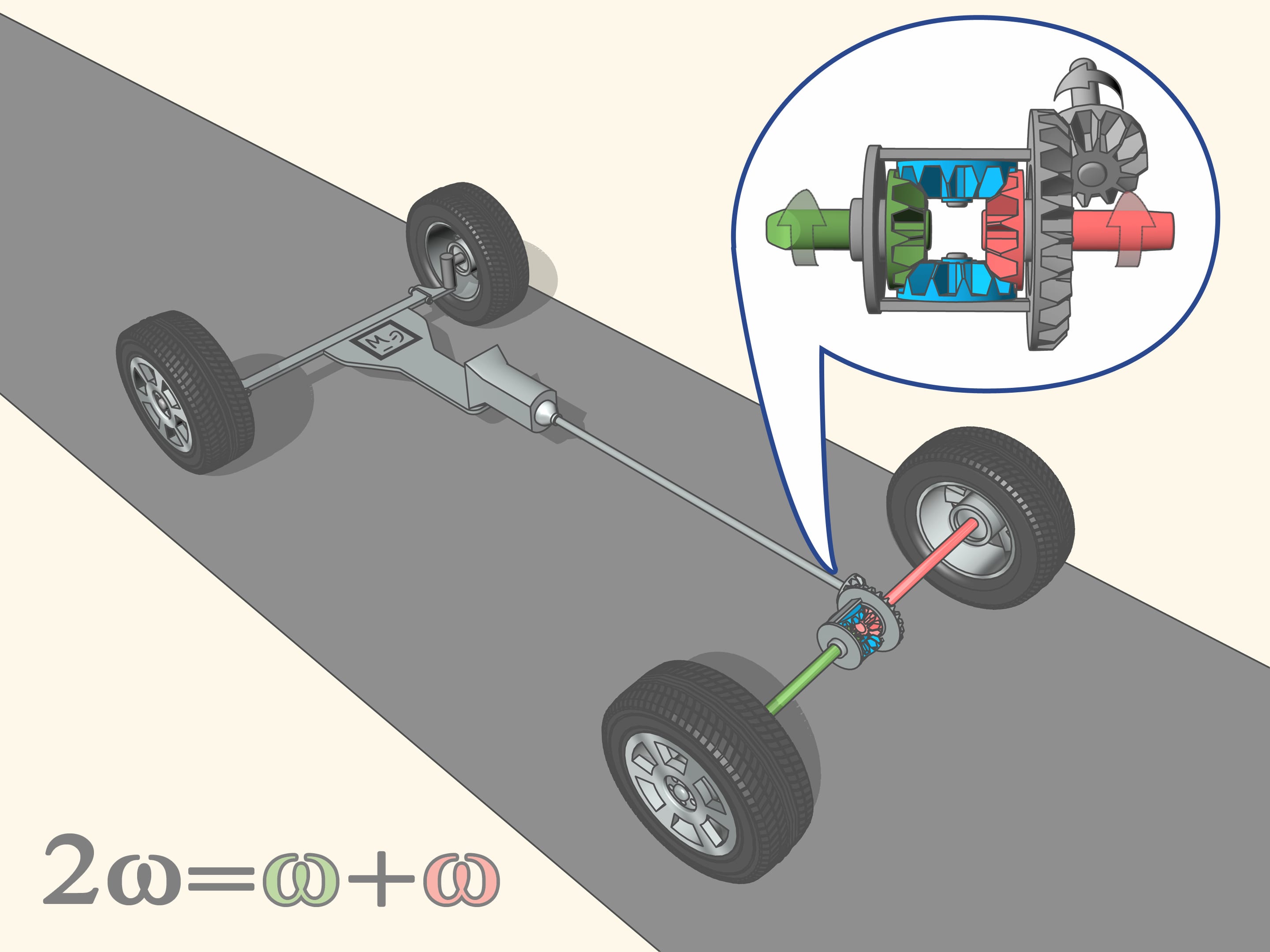
Pour cela c’est le différentiel qui vient nous aider, un typique «mécanisme planétaire». On appelle «planétaire» un mécanisme composé de mécanismes satellites tournant autour des axes qui à son tour bougent.
L’arbre d’entraînement grâce à la transmission donne la rotation à l’axe primaire, plus précisément, à travers le mécanisme planétaire, aux essieux droit et gauche. Quelle que soit la vitesse à laquelle les roues arrière tournent, la vitesse du mécanisme sera toujours égale à la vitesse moyenne des deux essieux. Chaque roue prend du différentiel une vitesse de rotation proportionnelle à la longueur de son parcours, de sorte qu’au total toute l’énergie est convertie en mouvement de la voiture.
Si la voiture se déplace sur une rue droite, et sous les roues motrices il y a le même type de sol, c’est à dire avec le même coefficient de friction, les roues du mécanisme prennent la même quantité de rotation de l’arbres d’entraînement et les essieux (et le roues avec eux) tournent à la même vitesse.
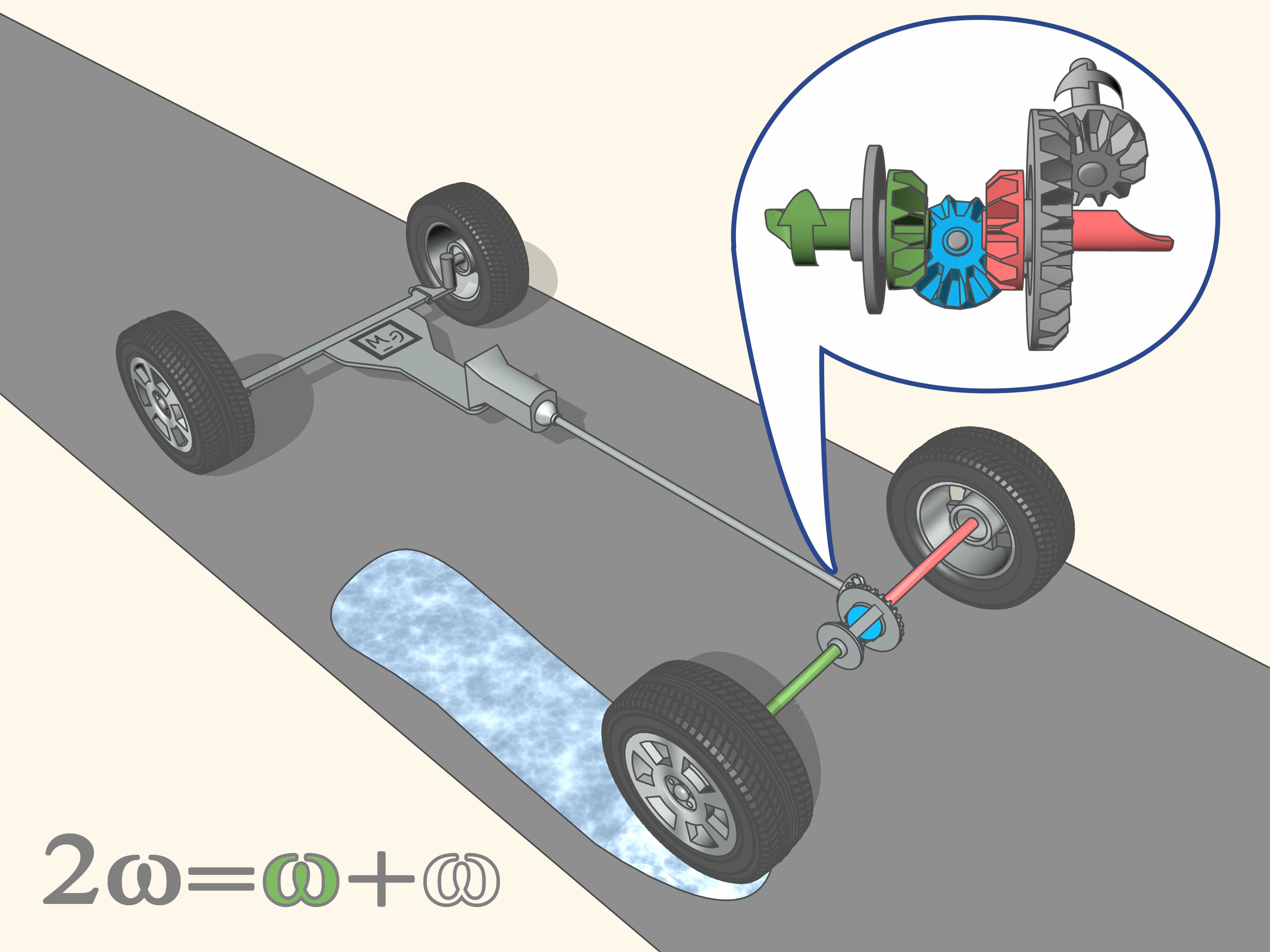
Mais si les coefficients de friction sont différents, par exemple, lorsque la voiture passe d’un coté sur une tache d’huile ou de la glace, alors... Comment tourneront les roues si cela arrive? Pour les roues non motrices, c’est assez simple: elles sont indépendantes les unes des autres, et ne doivent pas pousser la voiture, donc si l’une se retrouve sur la glace s’arrête de tourner, et le contrôle devient très faible.
Mais voila aussi la roue motrice arrière à gauche se trouve sur la glace. A droite le contrôle est élevé sur l’asphalte, mais à gauche, sur la glace, il est presque absent. En conséquence, la roue gauche tourne plus facilement, et elle commence à prendre de son côté toute la rotation, que le mécanisme répartit aux deux essieux. Puisque la quantité de vitesse totale, comme nous l’avons dit, est constante, si un essieux tourne très vite, l’autre ne tournera pas. Commencer à se déplacer dans cette situation, quand une des roues motrices a perdu l’adhérence avec le sol (par exemple, sur la glace), tandis que l’autre ne l’a pas perdue, c’est impossible.
Cela semblerait un défaut du différentiel. Les ingénieurs, en fait, cherchent toujours à améliorer le différentiel, tout en conservant sa propriété de base, qui est celle du contrôle optimal dans les virages, et en réduisant les effets désagréables, comme de ne pas permettre de tourner à un essieu lorsque la différence de vitesse est élevée. Mais il semble que jusqu’à présent rien n’a changé, comme les lois de la géométrie sont toujours les mêmes.