Si on enregistre un CD ou un DVD dans un ordinateur, la partie enregistrée du masseau semble plus sombre que la partie vierge.
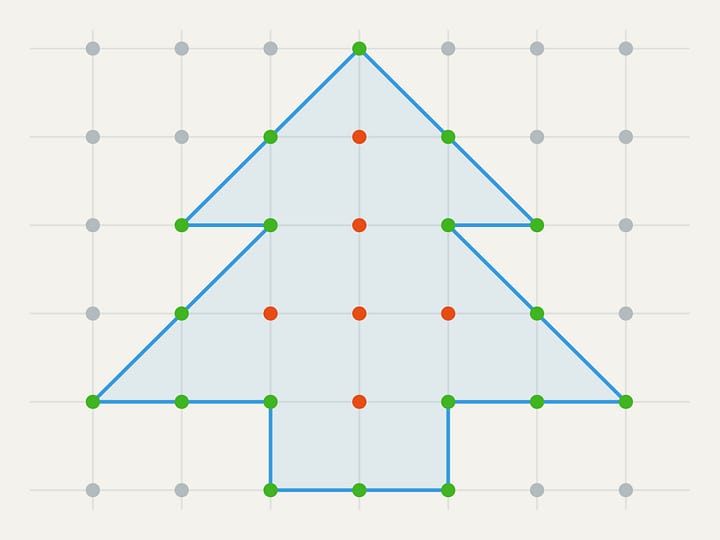
Laquelle des places disponible ou enregistrée, représentées sur l’image, est la plus grande?
D’un point de vue mathématique, un CD et un DVD sont des anneaux. Le rayon de la circonférence intérieure est un disque sur lequel rien n’est inscrit, mesurant 2 centimètres, mais le rayon de tout le cercle est de 6 centimètres. L’information s’inscrit en spirale, se déployant de la plus petite circonférence à la plus grande. Comme la longueur de la spirale correspond à la quantité d’informations, le volume des informations inscrites sur le masseau est proportionnel à l’aire de l’anneau occupé.
Commençons à enregistrer le disque comme le fait l’ordinateur. Si la largeur de l’anneau enregistré est égale à la largeur de l’anneau vierge, et est de 2 centimètres, nous verrons alors de combien l’aire de la partie utilisée est plus petite que la libre. De plus, si on ajoute à l’aire de l’anneau inscrit l’aire de tout le cercle intérieur, sur lequel rien n’est écrit, alors leur aire en somme sera de toute façon inférieure à l’aire de la partie vierge de base.
Pour que la moitié du masseau soit occupée de façon égale, l’anneau intérieur doit avoir un diamètre s’approchant de 2,5 centimètres, et l’anneau extérieur, environ 1,5 centimètres.
Qu’est-ce qui produit un tel effet?
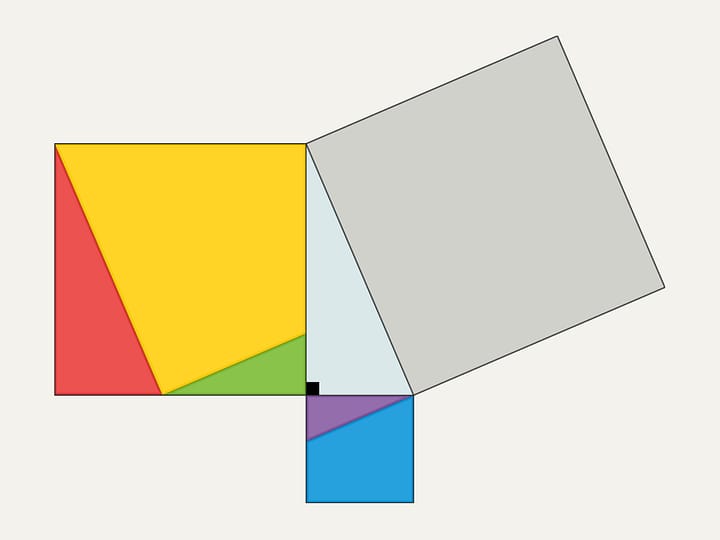
Un disque apparaît à la surface de la sphère, et, par conséquent, le volume est égal à l’aire de ce disque. Comme vous le savez bien, l’aire d’un disque de rayon $R$ est égale à $\pi R^2$. Pour calculer l'aire de l'anneau, on a besoin de soustraire de l'aire du grand disque l'aire du petit vierge: $\pi\cdot(R^2-r^2)$. Et comme ainsi tout dépend du rayon au carré, plus l'anneau décrit est proche du grand rayon, plus grande sera sa contribution à l'aire, avec le même diamètre.
Dans notre surface en 3D, le volume de la sphère dépend du rayon, élevé au 3è degré.
Cela signifie que l'effet considéré deviendra encore plus explicite: la grande partie du volume de la sphère est concentrée sur les bords? Quel volume est le plus grand dans cette orange? La peau ou la pulpe? La peau semble ne pas occuper un couche épaisse, mais est disposée dur le bord de la sphère. Son volume sur le dessin présenté est égal au volume de toute la partie mangeable de l'orange. En achetant une orange qui a une peau épaisse, vous achetez donc en majorité de la peau.