Après l’invention de la machine à vapeur par James Watt on chercha de résoudre le problème de la construction d’un mécanisme à charnières, qui allait transformer le mouvement circulaire d’une charnière dans le déplacement d’une autre charnière en ligne droite.
Pendant longtemps, les scientifiques et les ingénieurs ne pouvaient pas trouver la solution à ce problème. Ils réussirent à construire seulement des mécanismes capables de déplacer une charnière dans une ligne presque droite, mais pas parfaitement rectiligne. Ils ont été aidés, enfin, par une belle théorie mathématique.
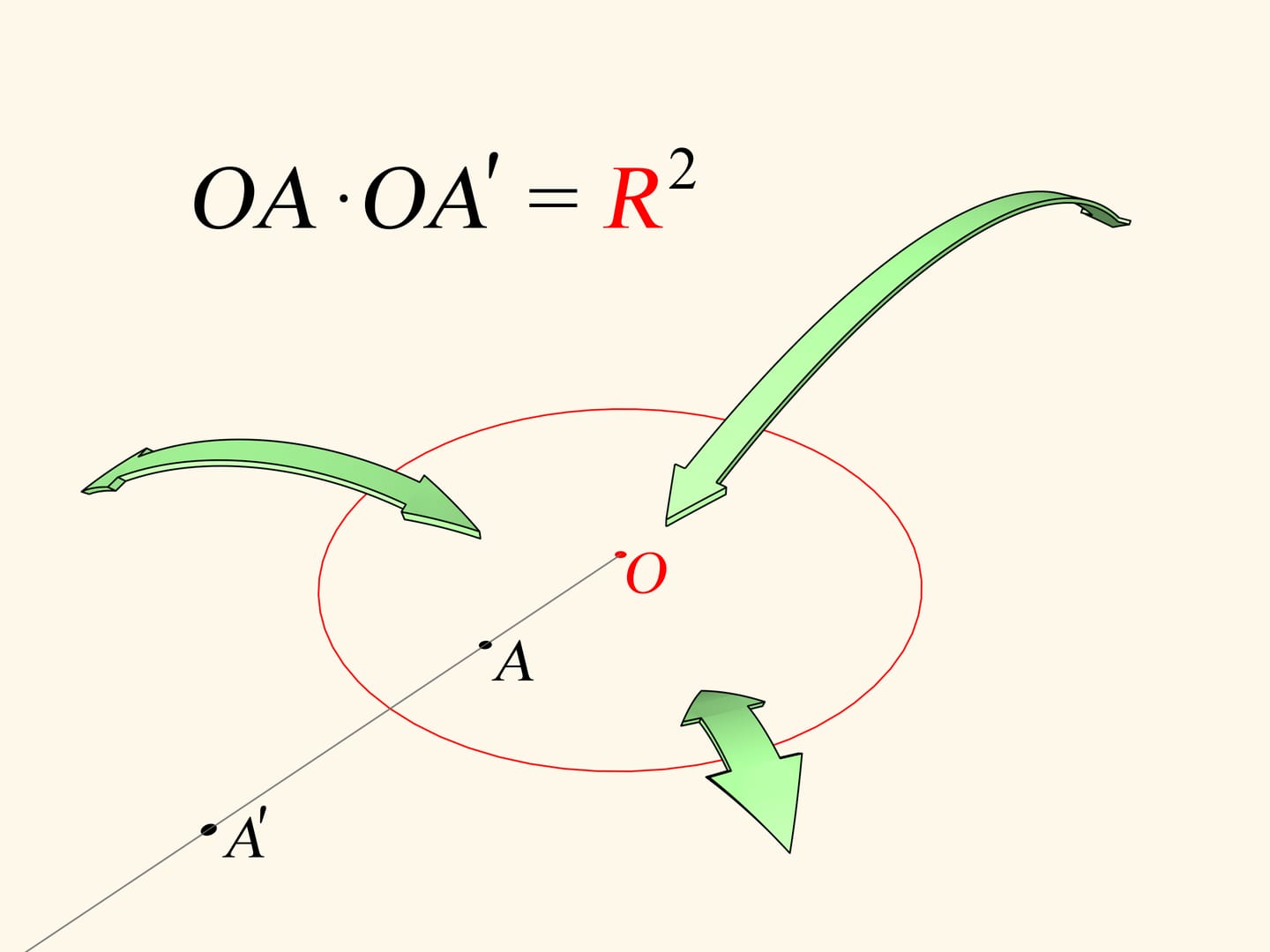
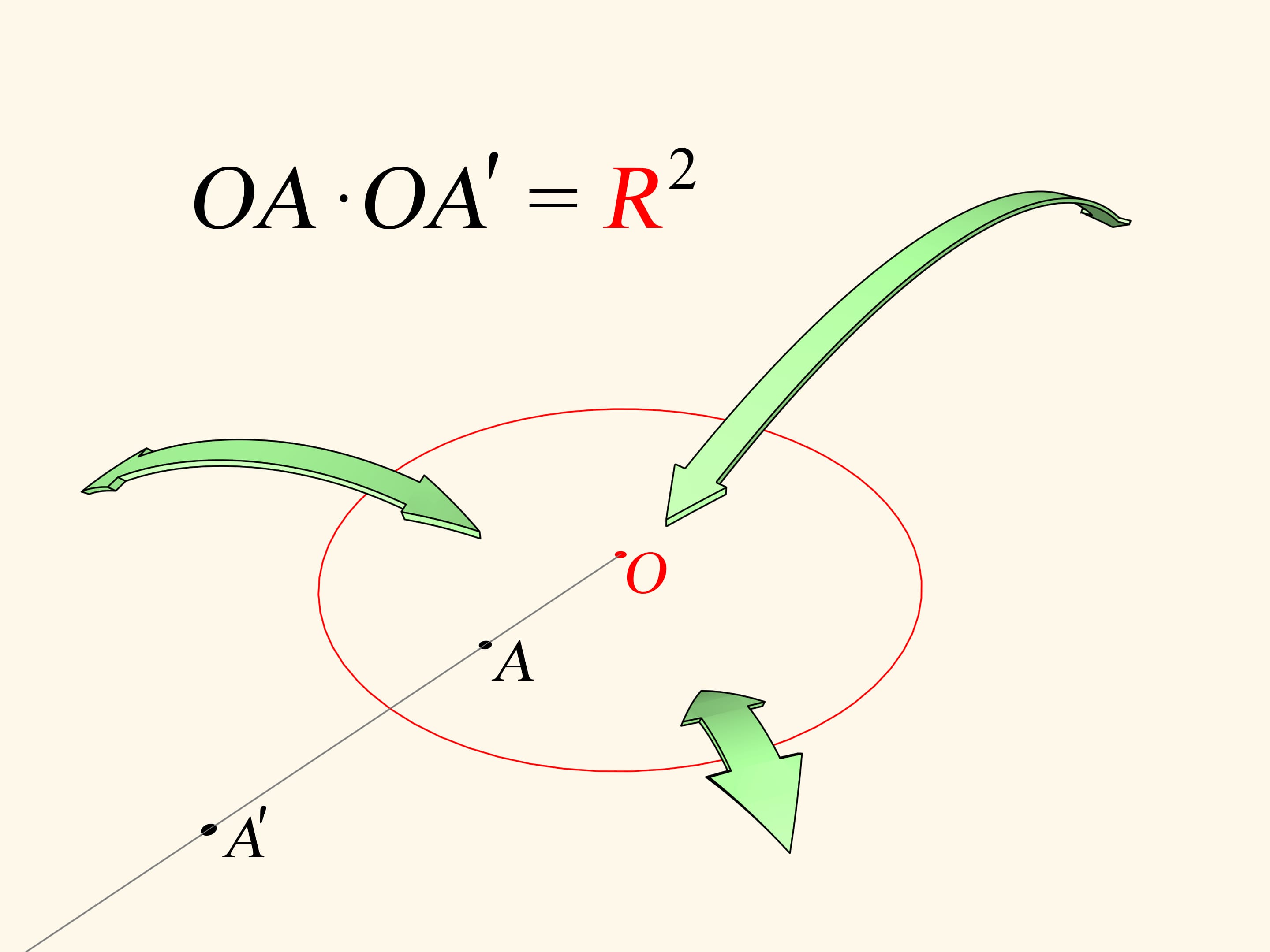
Rappelons que l’inversion dans le plan par rapport à un cercle est une application biunivoque de l’intérieur du cercle (à l’exception d’un point, le centre) dans le reste du plan en dehors du cercle. L’image du point $A$ est le point $A’$, qui se trouve sur le rayon du cercle passant par le point $A$. Sa position sur le rayon est définie par l’égalité $OA \cdot OA'=R^2$, où $O$ est le centre du cercle, et $R$ est la longueur de son rayon. Par l’aide de l’inversion on résout de nombreux problèmes de géométrie. Comme nous le verrons, cette application nous permet de résoudre non seulement des problèmes théoriques.
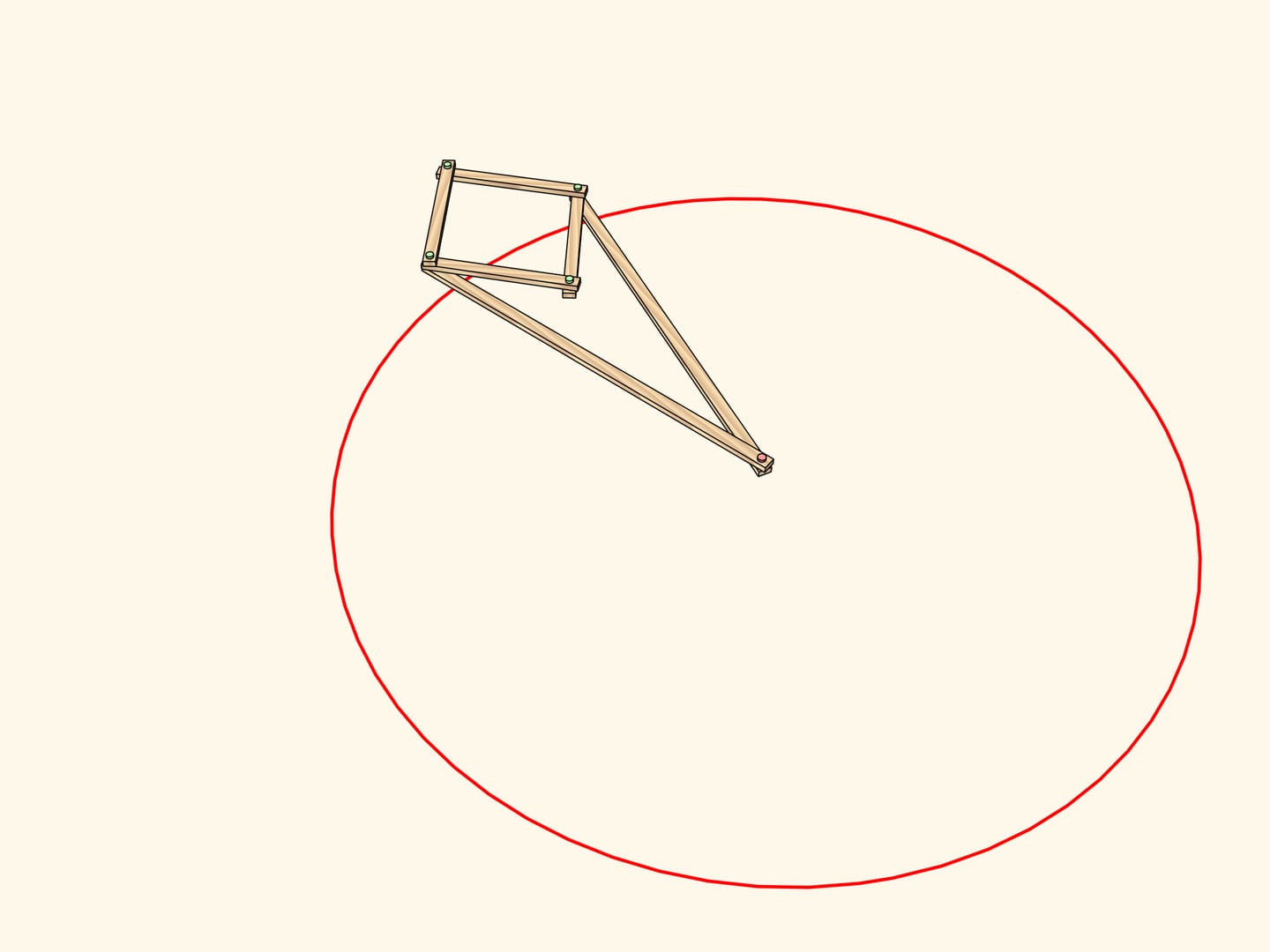
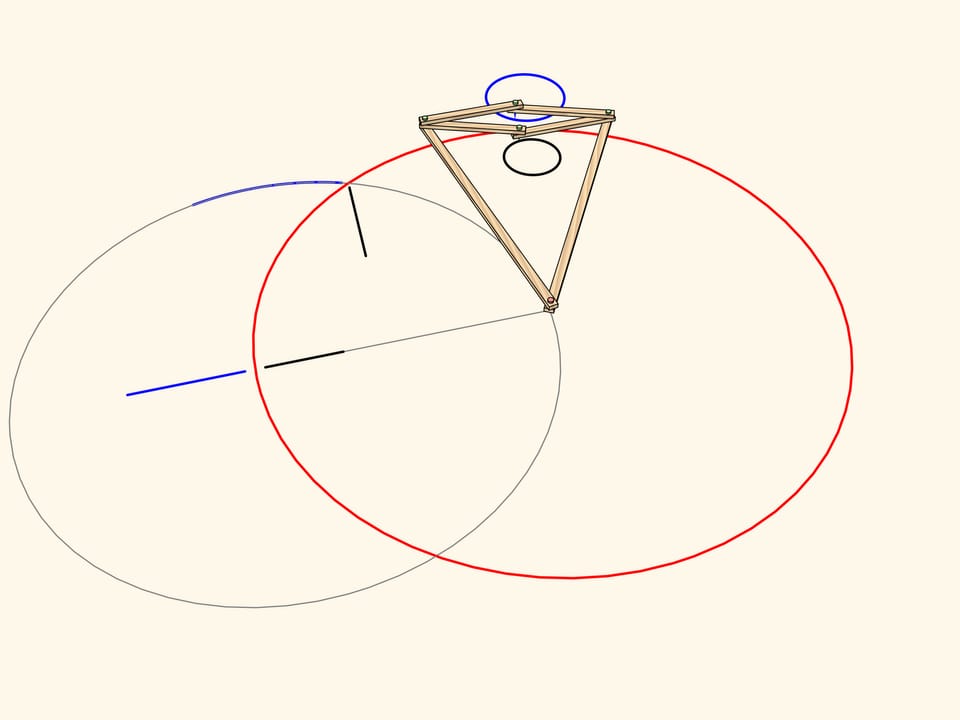
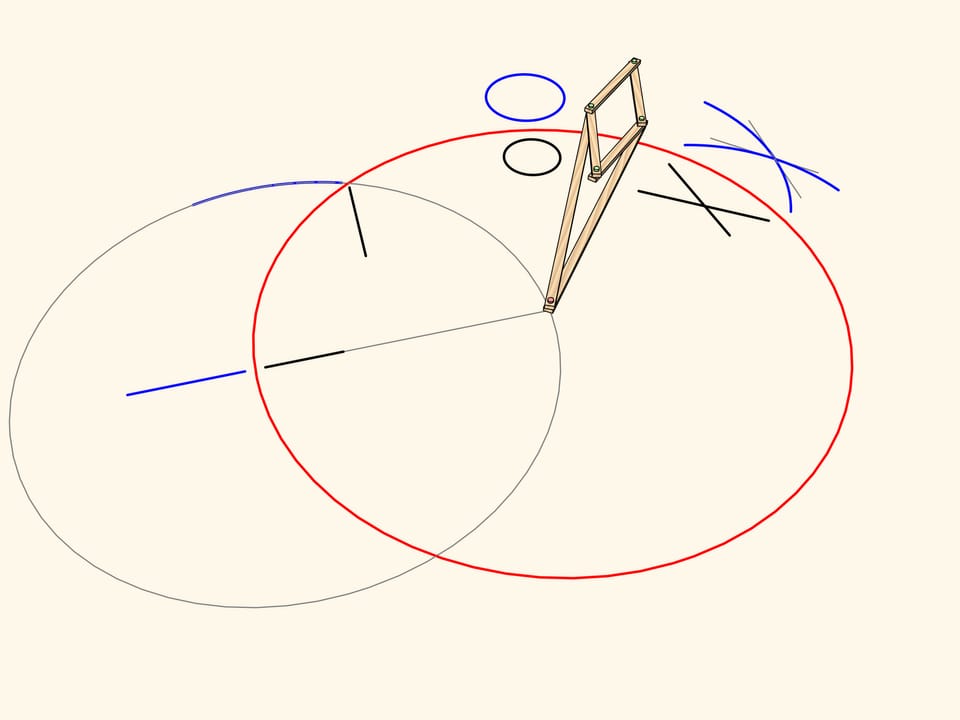
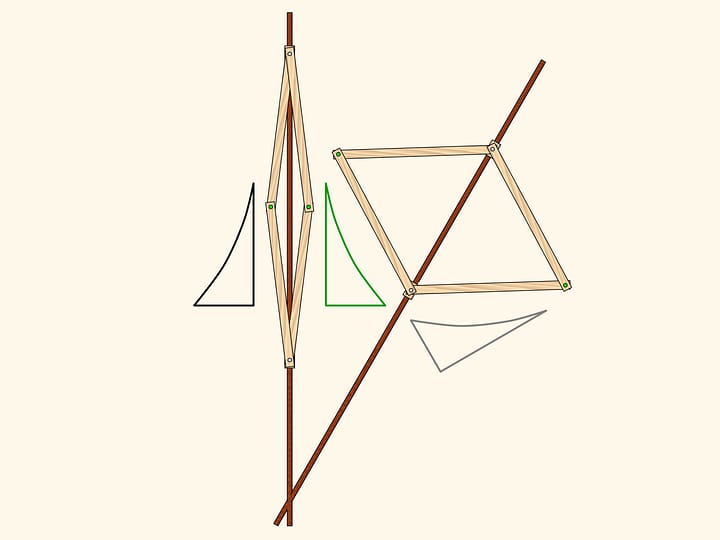
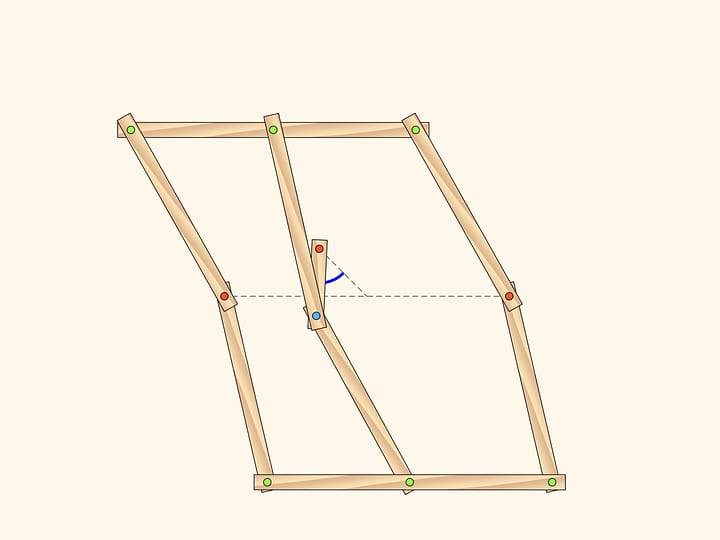
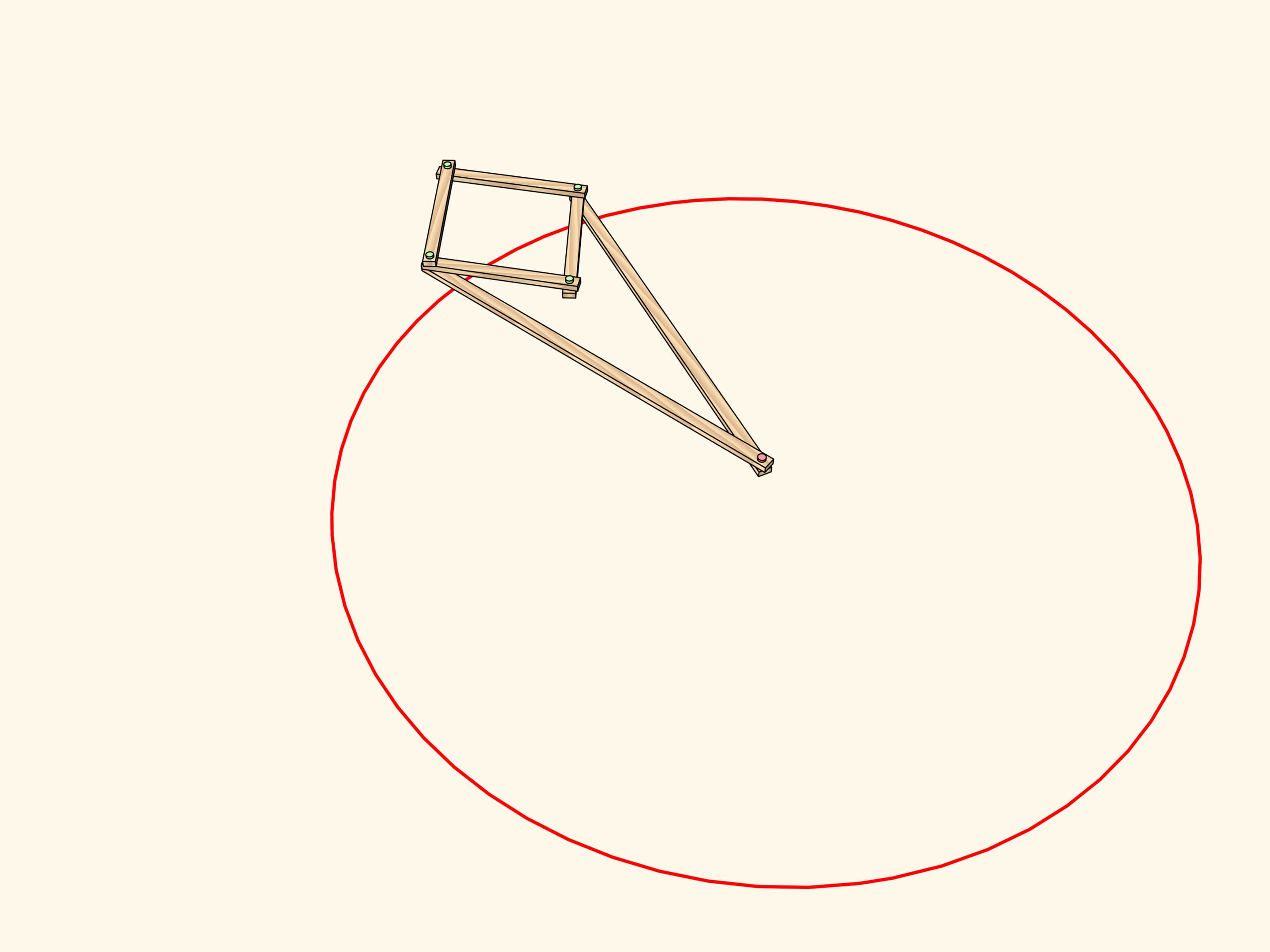
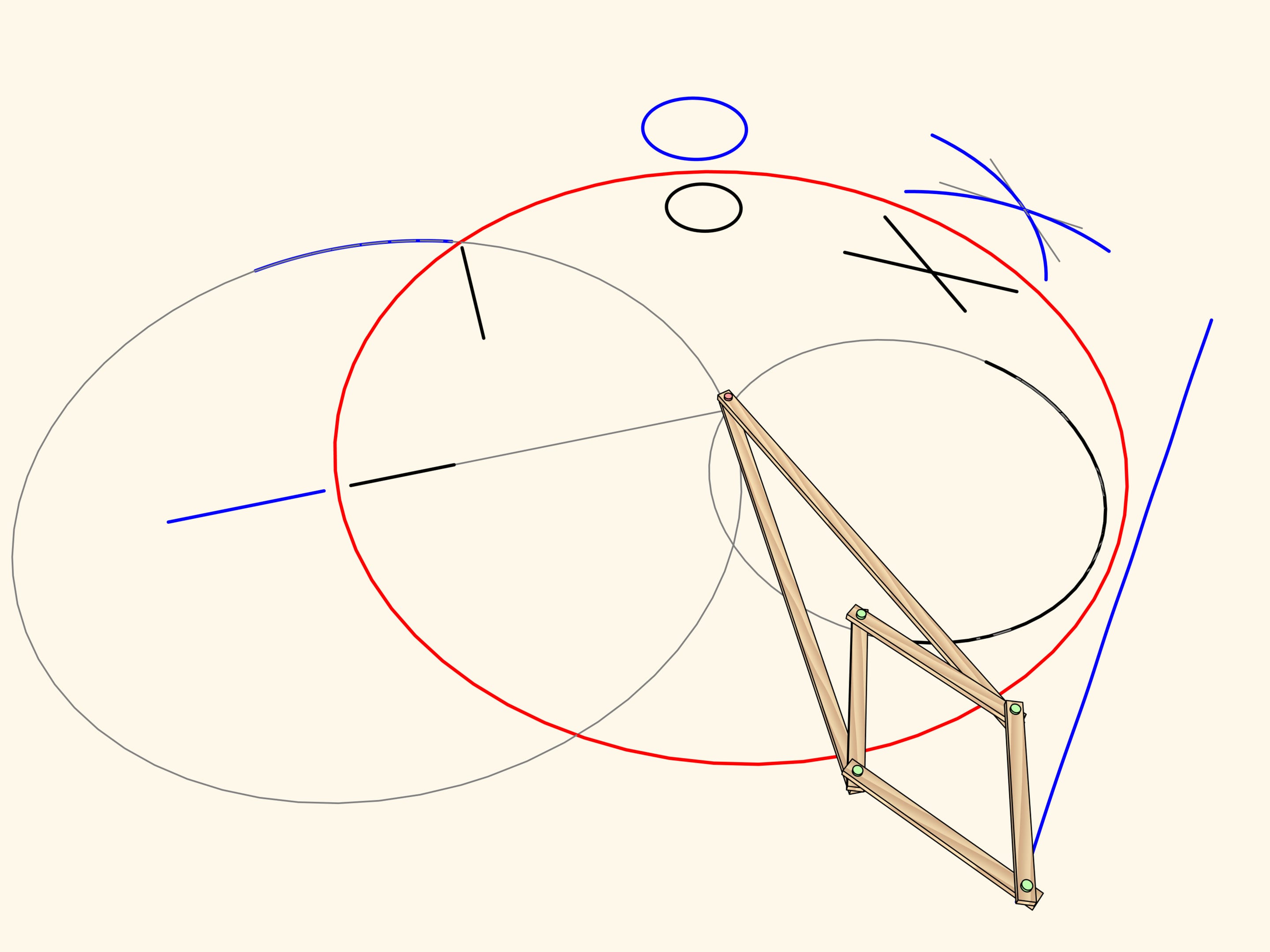
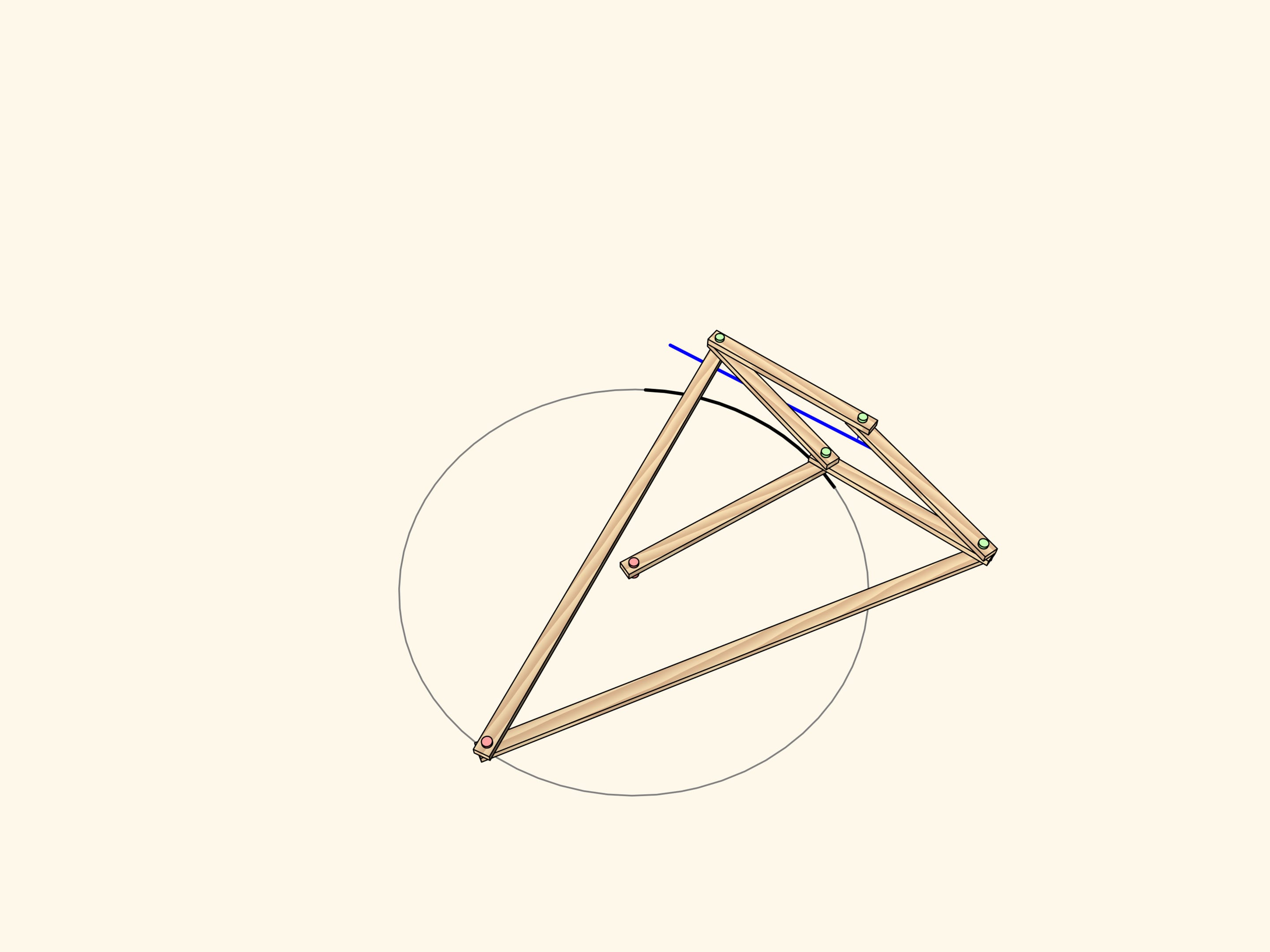
Considérons un mécanisme avec une charnière appliquée à un point fixe (marqué en rouge). Deux barres de la même longueur sont allachées par une extrémité à cette charnière, tandis que les autres extrémités sont attachées aux deux charnières opposées d’un losange composé de quatre barres reliées par quatre charnières.
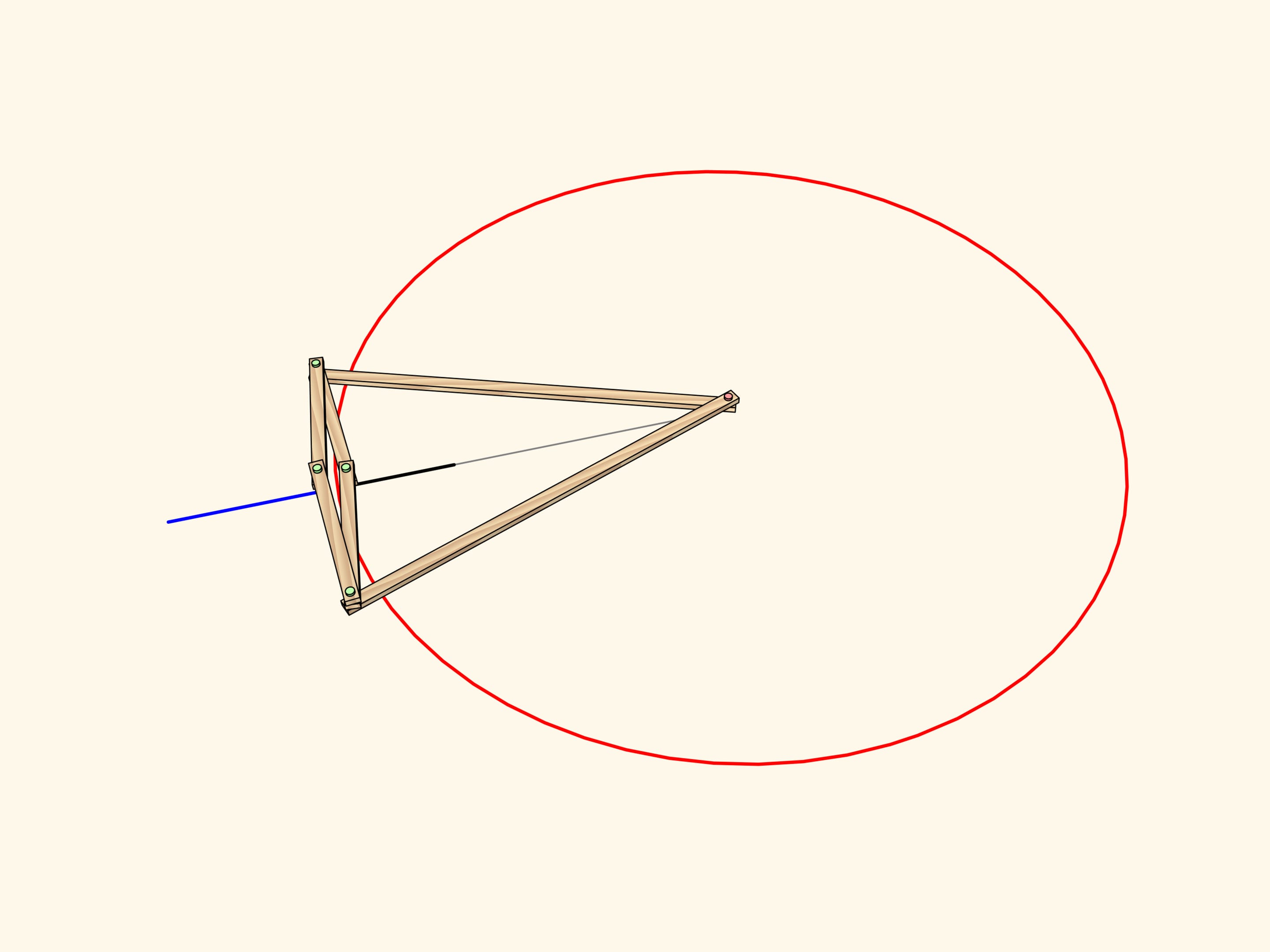
Ce mécanisme réalise l’inversion par rapport au cercle centré au point fixe et avec rayon qui dépend de la longueur des éléments du mécanisme. La courbe tracée par l’une de deux charnières libres du losange est l’image, par inversion, de la courbe tracée par l’autre.
Par l’aide de notre mécanisme nous observons maintenant quelles propriétés l’application de l’inversion possède.
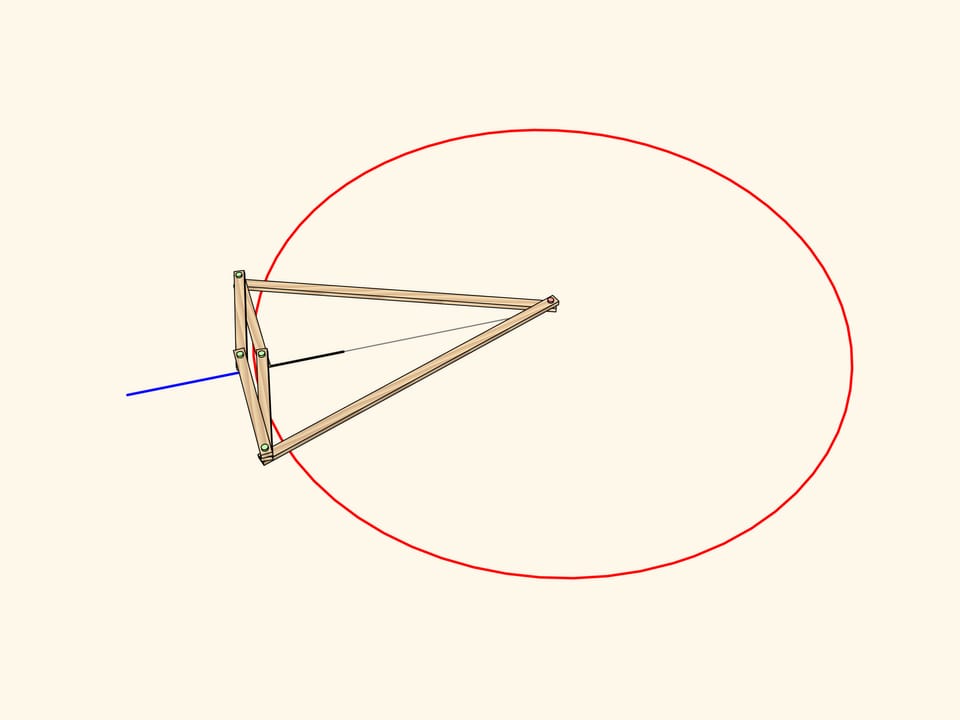
De la définition même de l’inversion il est évident que l’image d’un segment, qui est sur une ligne droite passant par le centre du cercle est un segment qui se trouve encore sur la même ligne.
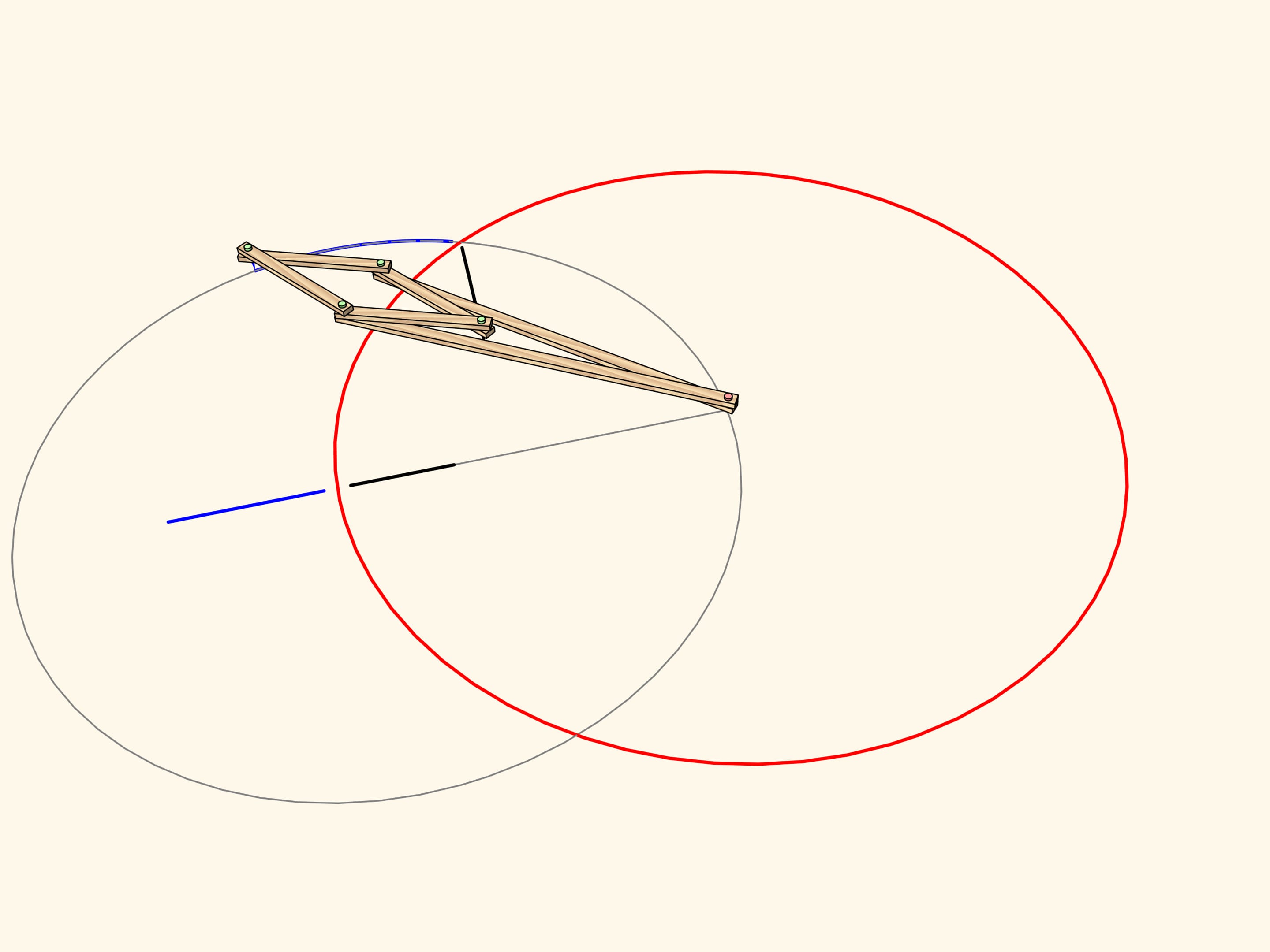
L’image d’un segment, qui est sur une ligne droite qui ne passe pas par le centre d e l’inversion, est un arc de cercle, passant par le centre de l’inversion.
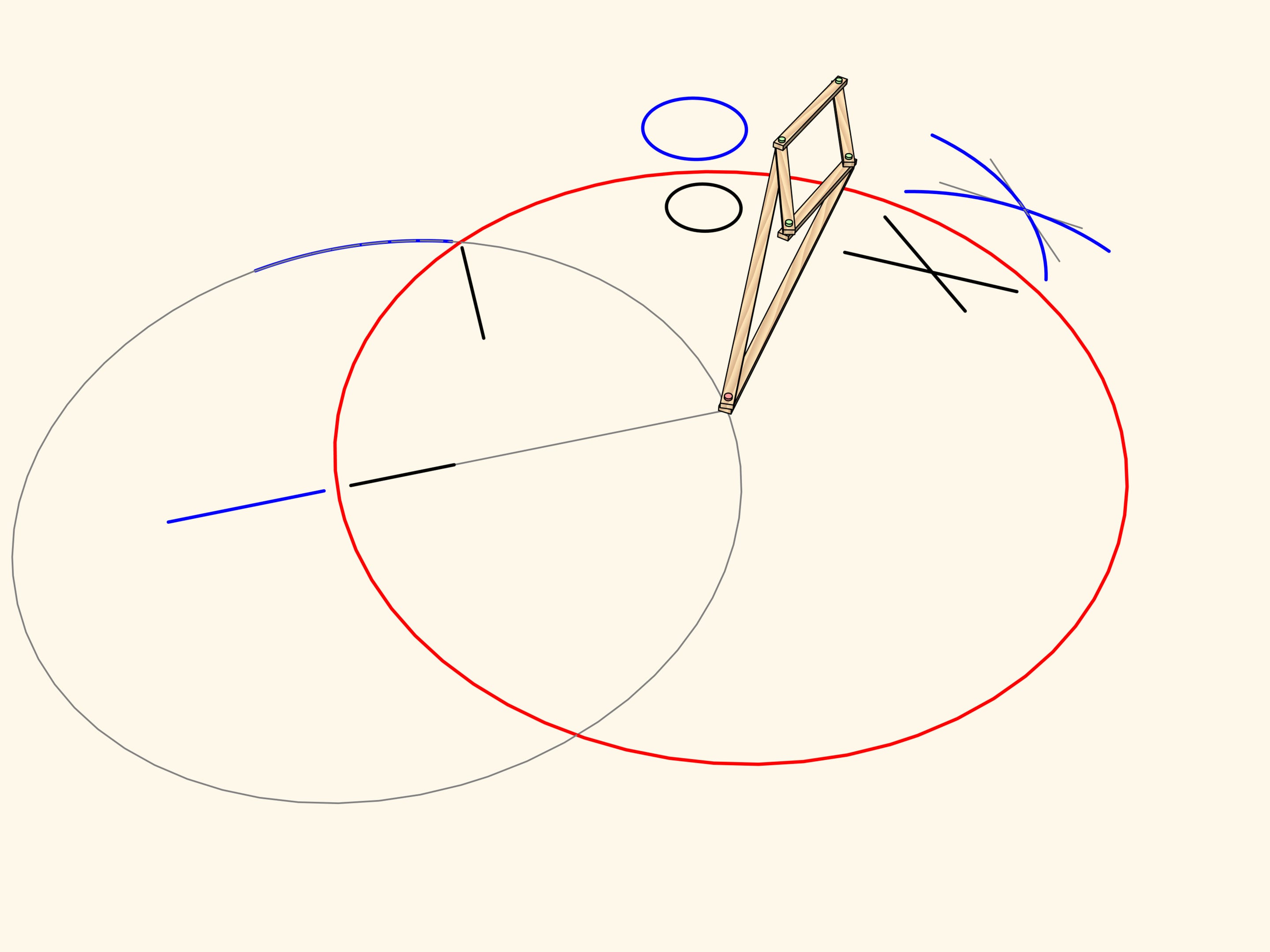
Un cercle qui ne passe par le centre et qui ne coupe pas le cercle de l’inversion, est transformé par l’inversion dans un autre cercle.
L’inversion conserve les angles entre deux courbes, cependant, renverse les orientations. Telles applications en mathématiques sont appelées «anti–conformes» (conformes sont celles qui conservent soit les angles soit les orientations).
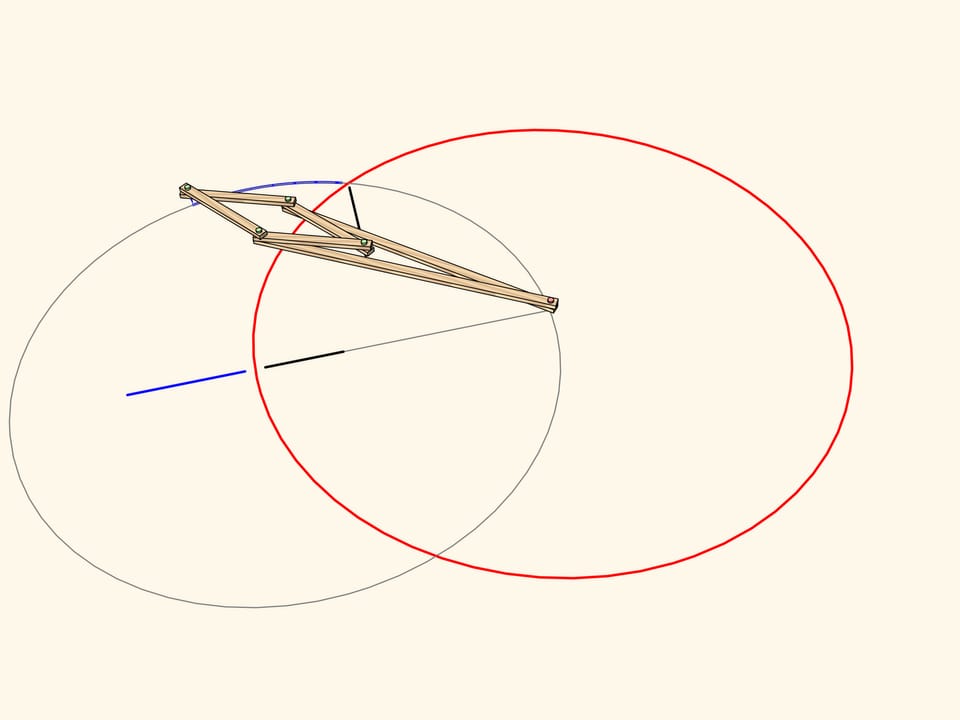
Un arc de cercle, passant par le centre de l’inversion est transformé... exactement dans un segment de ligne droite!
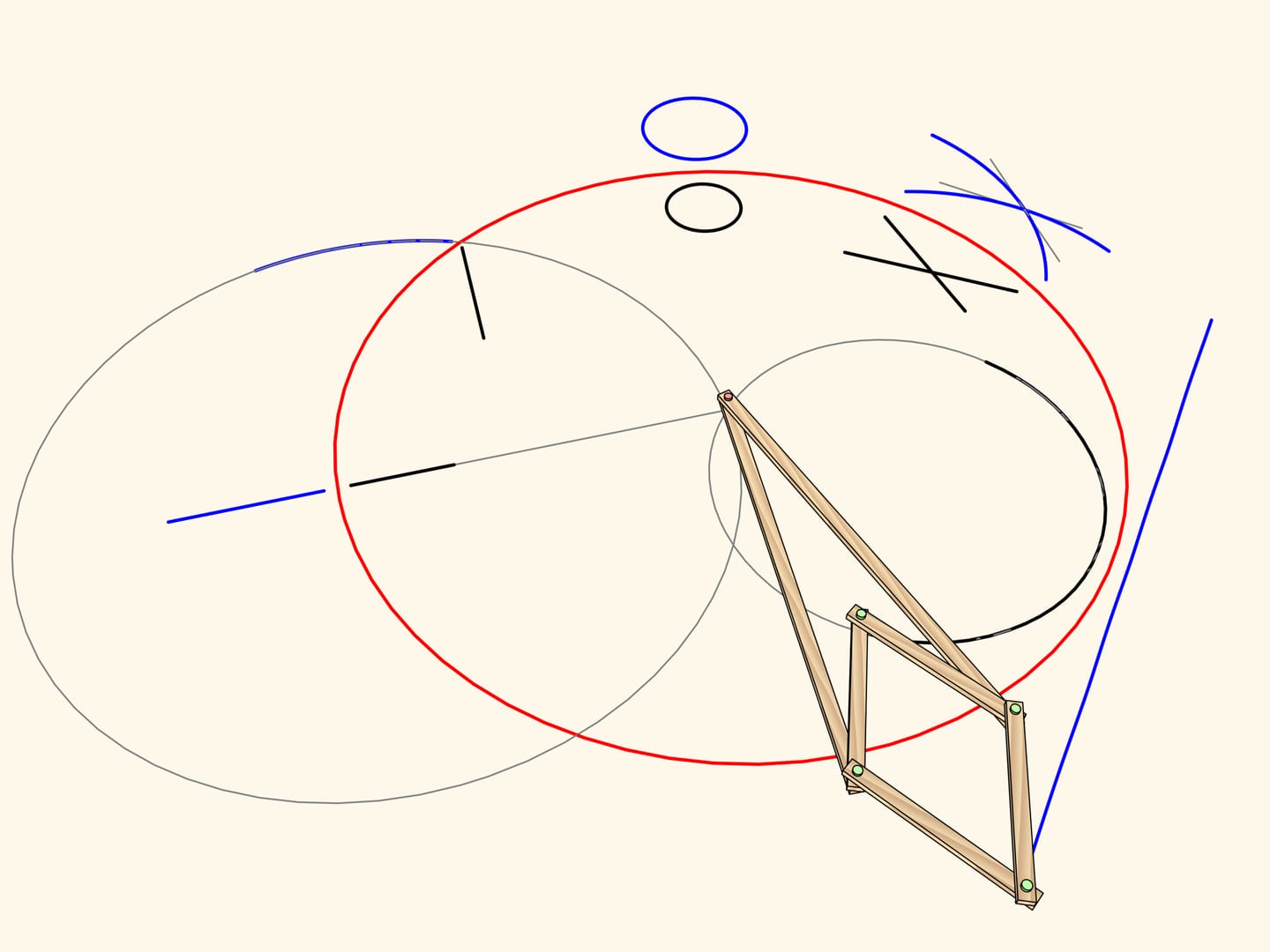
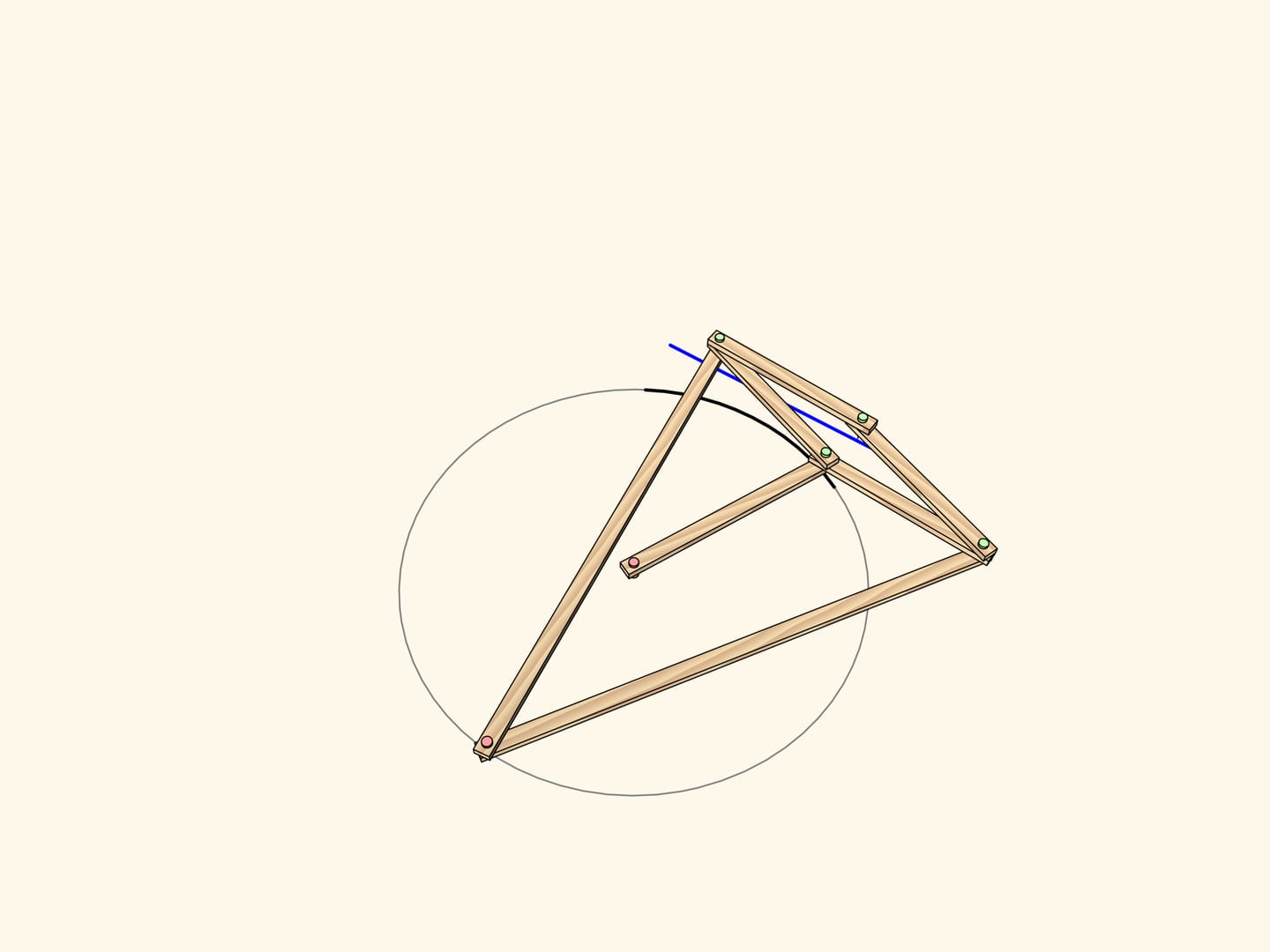
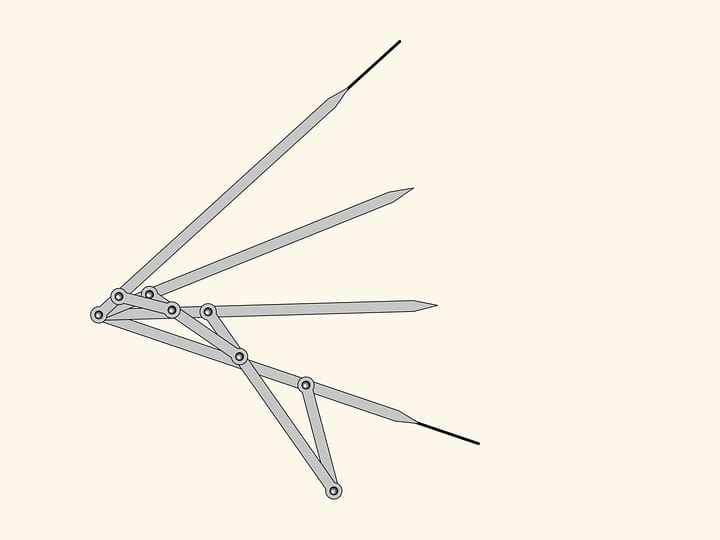
C’est précisément cette propriété qui a été utilisé dans la construction du premier mécanisme capable de tracer segments de lignes droites. Pour qu’une charnière du losange dessine un cercle passant exactement par le centre du cercle de l’inversion, nous ajoutons une charnière fixée au centre du cercle passant par le centre de l’inversion, et une barre aussi longue que son rayon, fixée aux extrémités à cette charnière et à une charnière du losange. La trace de l’autre charnière sera toujours un segment de droite. En raison du fait qu’on utilise la propriété d’inversion, ces mécanismes sont souvent appelés inverseurs.
Peaucellier (Peaucellier Charles Nicolas, 1823—1913) informa les officiers du Corps d’Armée des ingénieurs de la construction d’un inverseur en 1864 dans une lettre privée. Toutefois il ne fut pas capable de fournir de détails sur la construction du mécanisme. En 1868, Lipman Lipkin (1846—1876), élève de Thchebyshev, inventa l’inverseur. Son article détaillé a été publié en 1870, et l’article de Peaucellier n’apparu qu’en 1873, avec la description de ce mécanisme, faisant référence au travail de Lipkin.
Ensuite d’autres mécanismes ont été inventés pour dessiner des lignes droites, basées sur d’autres idées mathématiques. Mais l’inversion se distingue par sa beauté, ses bonnes propriétés mécaniques et a trouvé de nombreuses applications en ingénierie.