Beaucoup de garçons voudraient aller dans la cabine de pilotage du métro. En fait, aller tout droit dans un tunnel, qui est simplement un cylindre, ce n’est pas si excitant. Autre chose sont les virages.
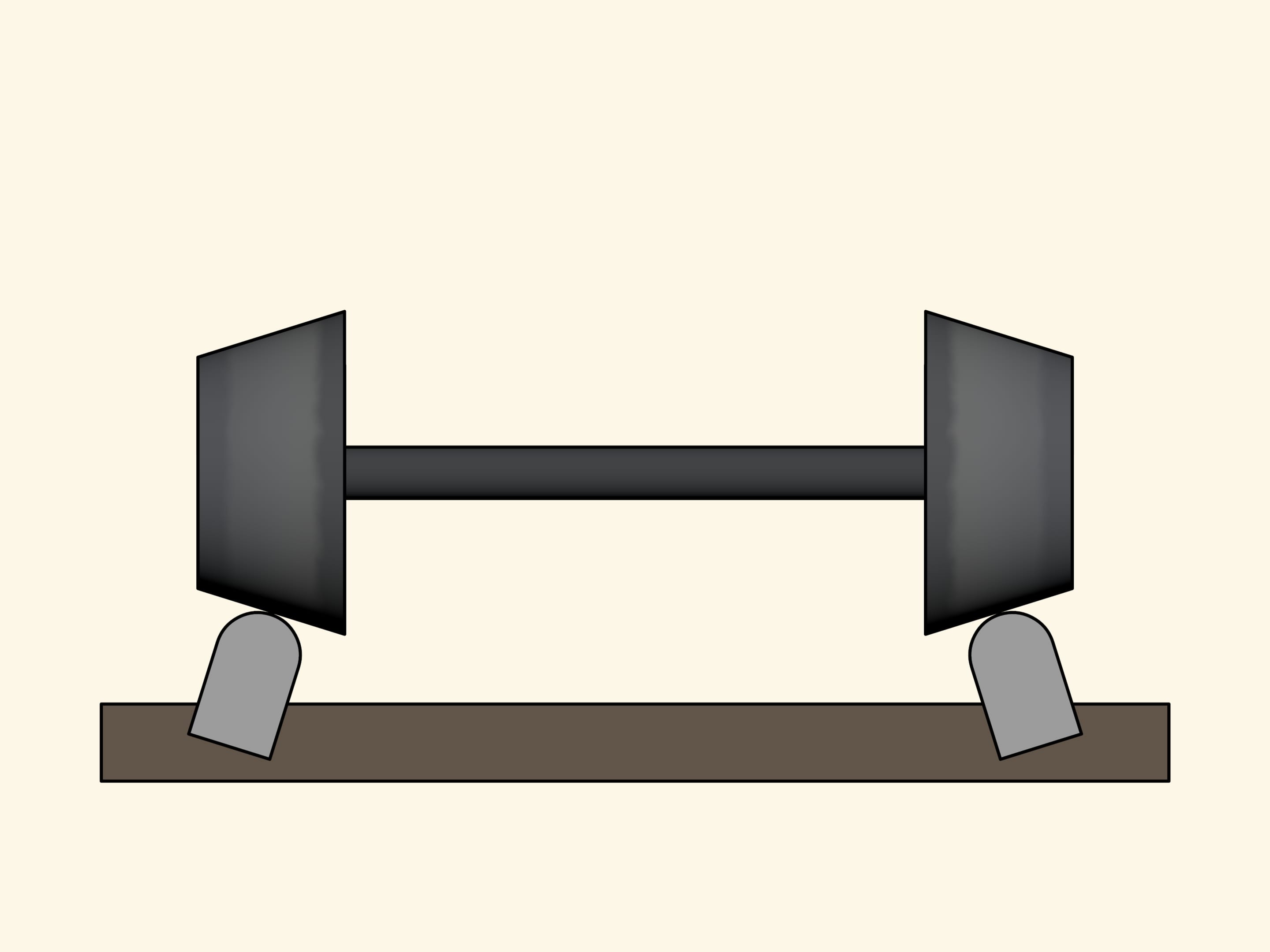
Mais comment les wagons braquent sur les rails? En fait, la roue droite et la roue gauche sont fixées rigidement ensemble. Par ailleurs, dans un virage le rayon de courbure du rail extérieur est plus grand que le rayon du rail intérieur, donc la longueur de l’arc de cercle qui est parcouru par la roue à l’extérieur est plus grande de la longueur du chemin de la roue à l’intérieur. Et il est nécessaire qu’aucune des deux roues ne dérapent sur le rail.
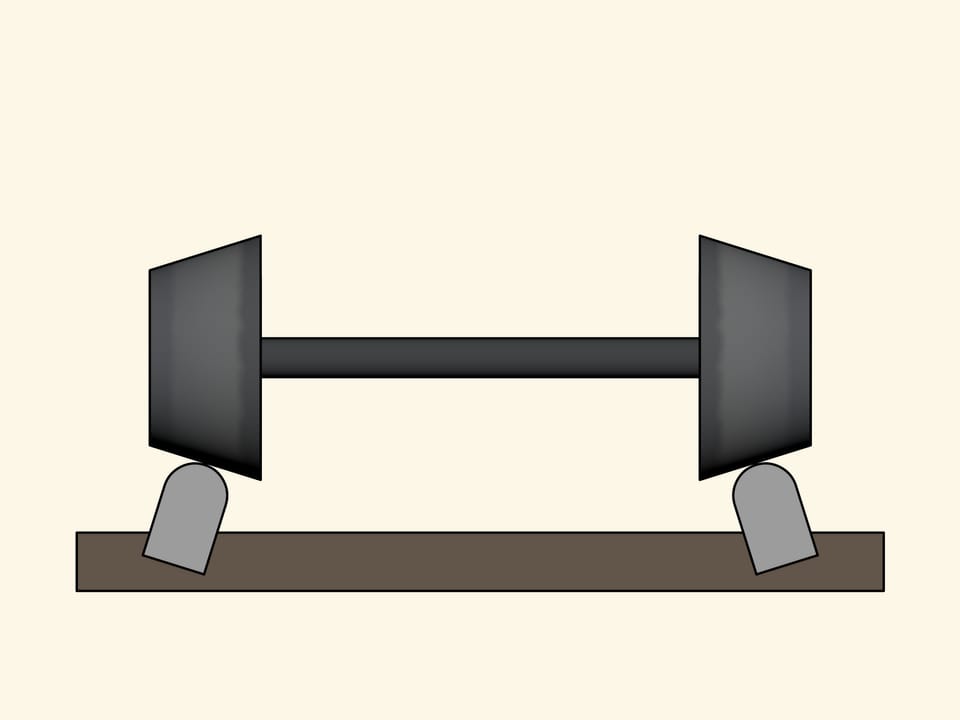
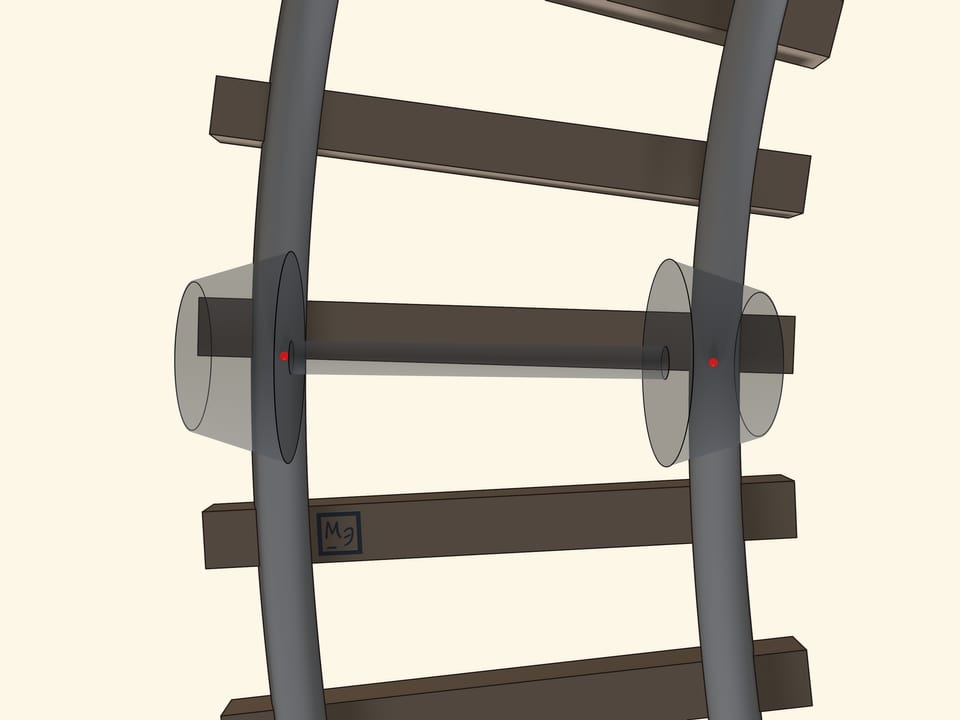
Considérons un modèle simplifié qui explique pourtant bien ce qui essentiellement se passe. Les roues de ce modèle sont deux cônes tronqués identiques et sont rigidement fixée à l’axe. Le profil de la surface du rail est un arc de cercle. Si les rails avaient été plantés verticalement, ils subiraient une poussée supplémentaire, puisque le chargement de la roue exerce le pois sur le rail perpendiculairement à sa surface. Par conséquent, les rails sont plantés un peu inclinés en dedans, de sorte que l’axe de leur profil est perpendiculaire à la surface des roues coniques.
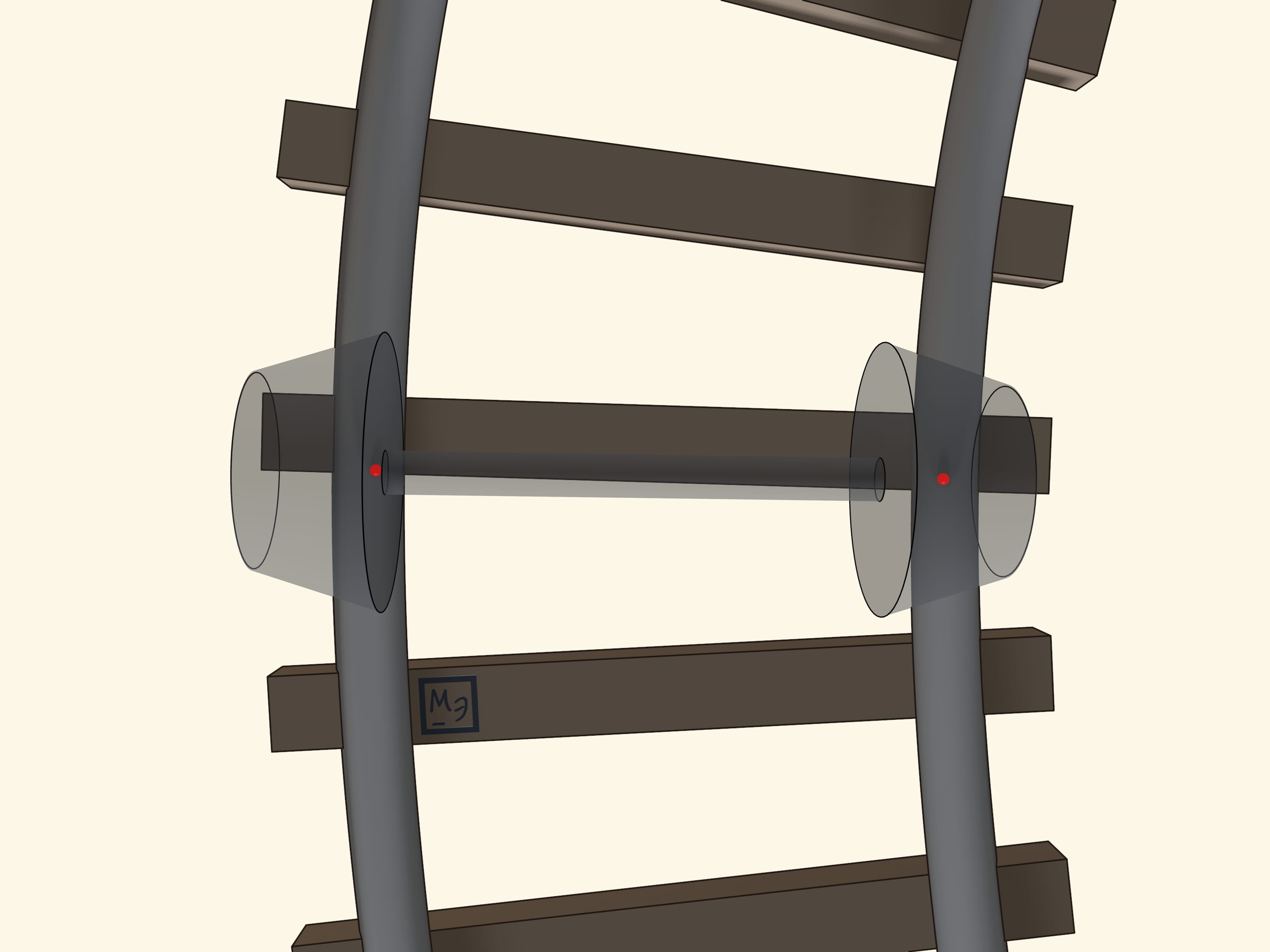
Nous suivons maintenant une paire de roues qui prennent un virage. Il arrive qu’elle se déplacent par rapport à la voie!
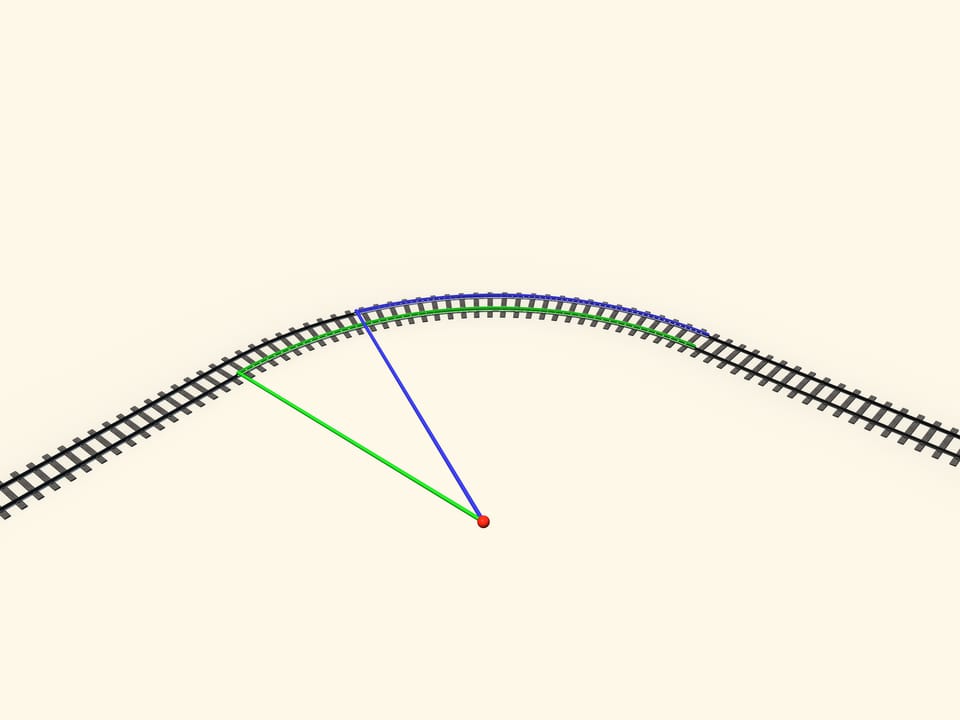
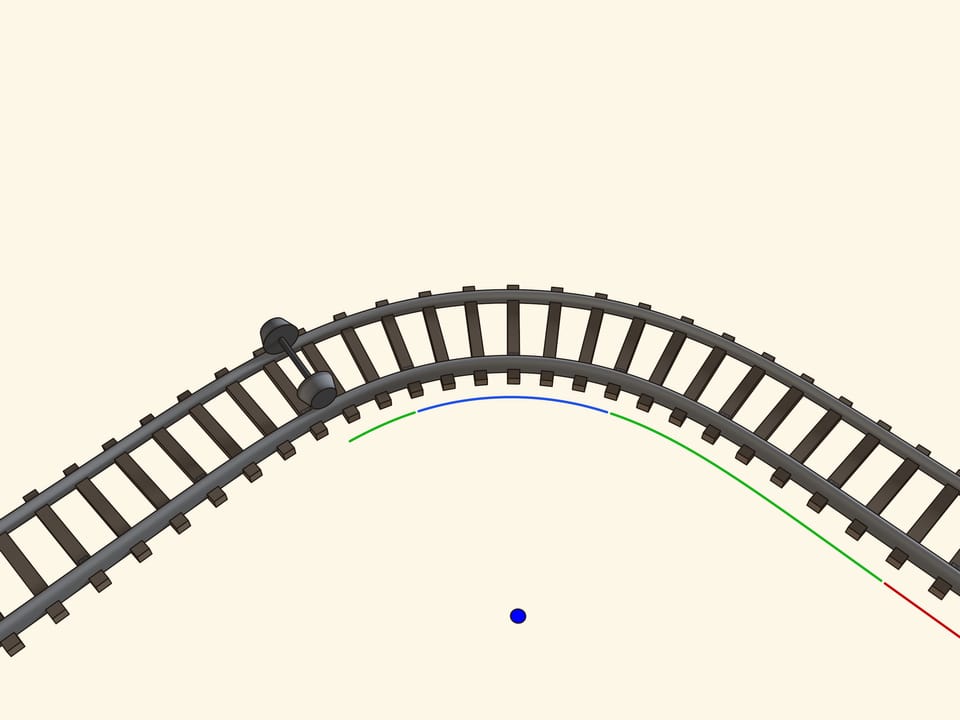
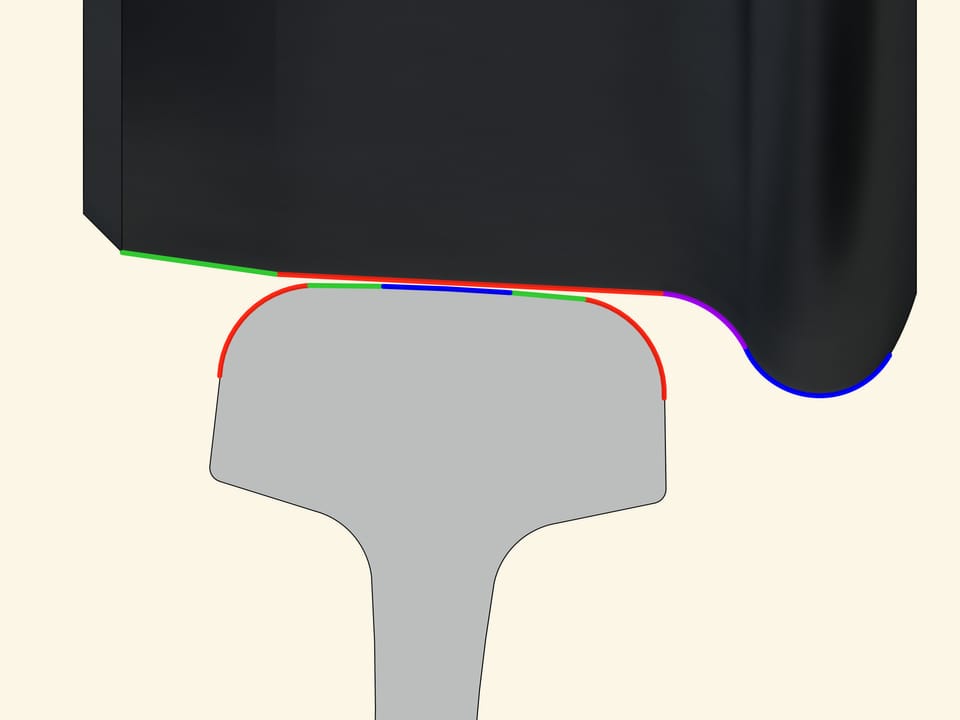
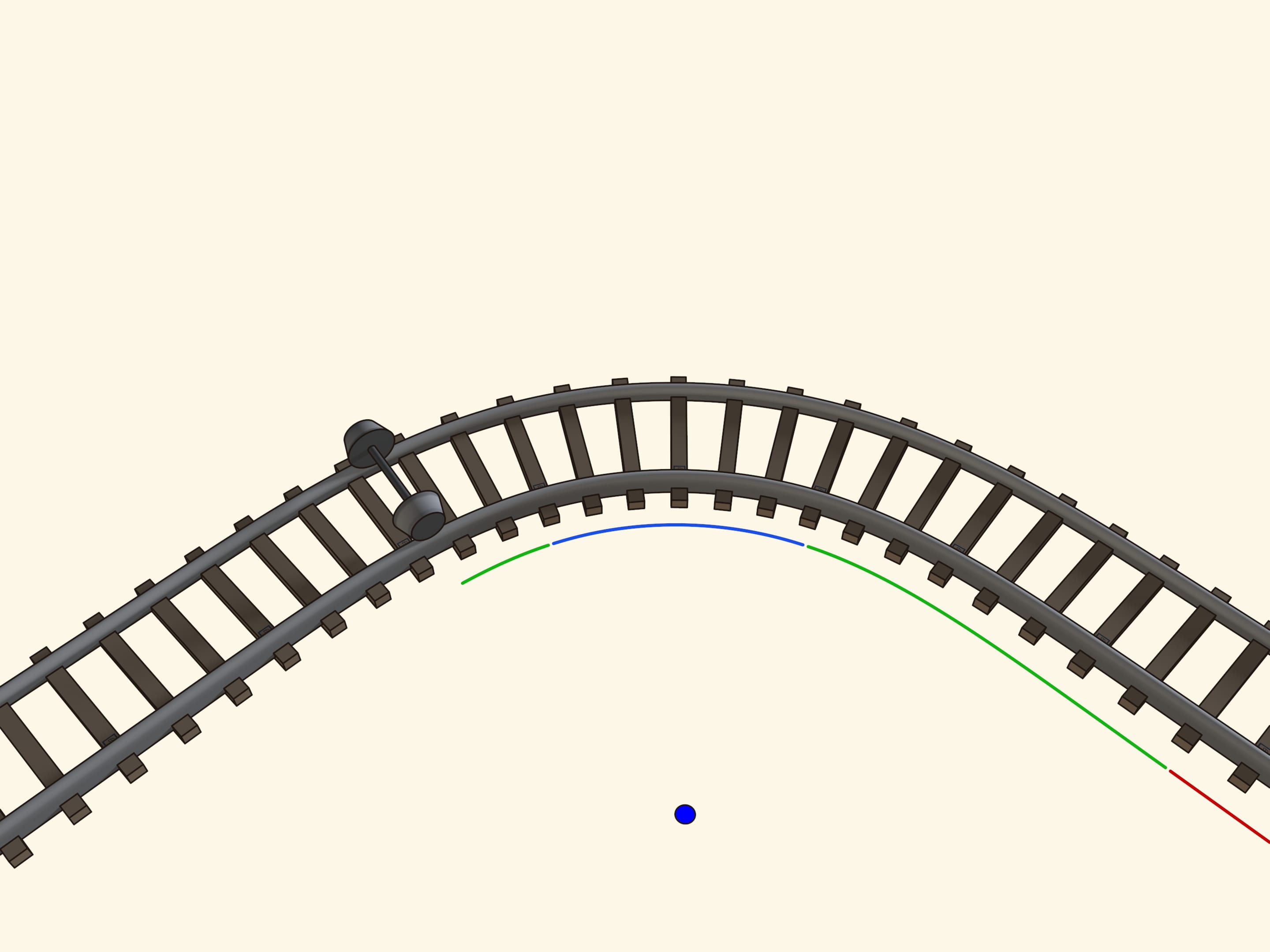
Observons comment une courbe est faite. Après un bout rectiligne commence un bout avec rayon de courbure variable, enfin il y a un morceau avec un rayon constant, c’est à dire un arc de cercle. Pour s’assurer que les passagers ne souffrent pas de secousses par les côtés du wagon lorsqu’il passe entre deux bouts différents, une condition plutôt forte doit être satisfaite: la dérivée seconde de la trajectoire doit être continue aux points de transition entre un morceau et l’autre.
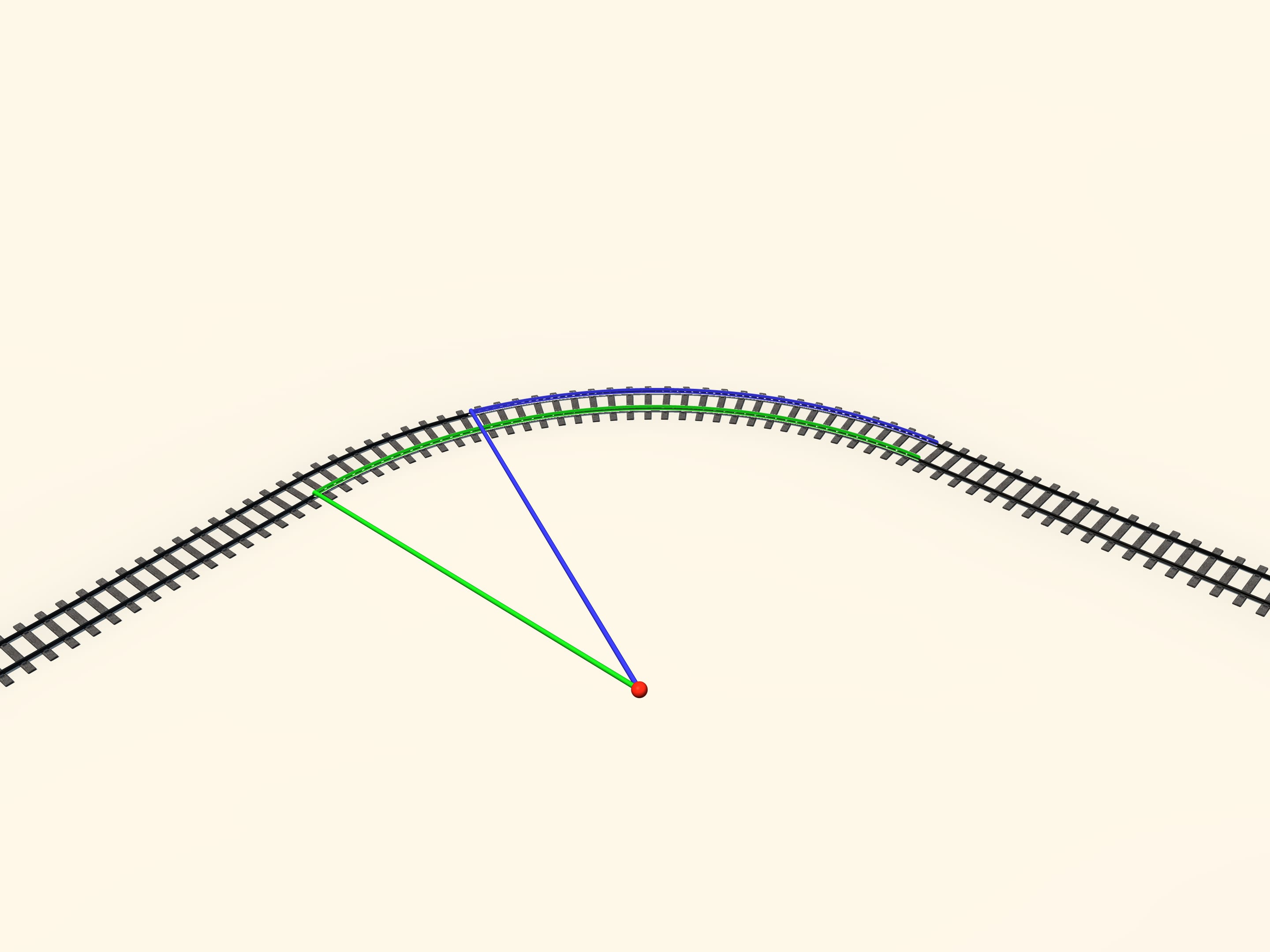
La tangence entre la roue conique et la surface du rail est faite de points. Au virages le point de tangence se déplace sur le cône. Dessinons les cercles constitués de tous les points de tangence. Quand l’axe est situé exactement au milieu, c’est à dire dans un morceau droit, ces cercles sur les deux roues attachées au même axe sont égaux. Mais quand l’axe est déplacé, en prenant un virage, le cercle sur la rue à l’intérieur est plus petit du cercle sur la roue à l’extérieur. Donc on peut considérer que les roues ont des rayons variables. Et puisque le rayon de la roue à l’intérieur est plus petit que le rayon de la roue à l’extérieur, quand les roues tournent sur les rails sans déraper, le chemin parcouru par la roue à l’intérieur est plus court que celui de la roue à l’extérieur.
Mais pourquoi dans un virage les roues se déplacent sur les rails? Il s’avère que la physique n’est pas impliqué. C’est juste une question de géométrie, et aussi d’une géométrie très belle! Lorsque les rails se courbent, ils provoquent un déplacement de la paire de roues exactement d’autant qu’il faut afin que la roue à l’intérieur et celle à l’extérieur roulent sans déraper.
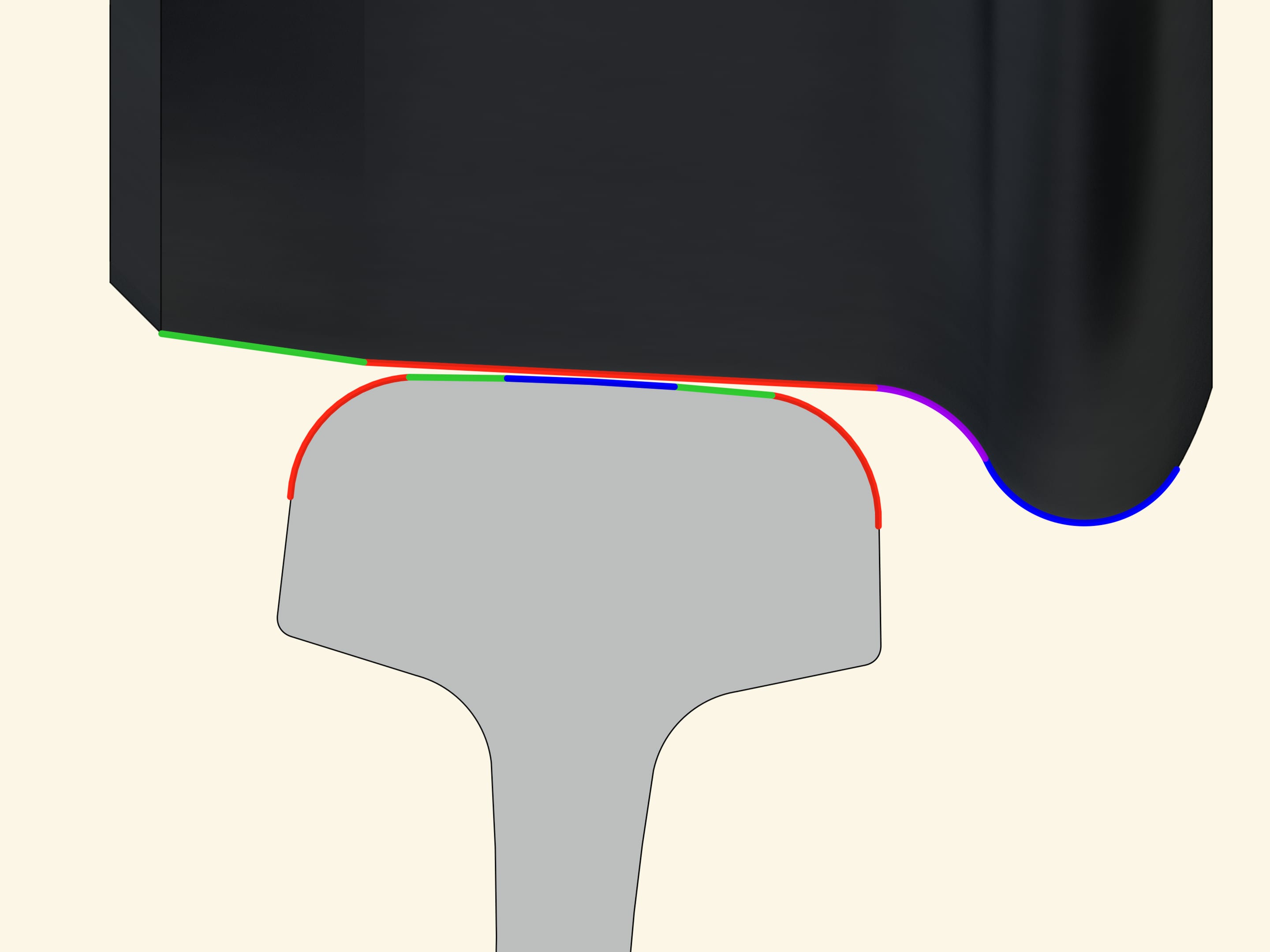
Un bon modèle doit prendre en compte les propriétés les plus importantes des objets en cours d’examen et négliger les détails. Tel a été notre modèle, mais en réalité tout est plus complexe. Selon la compagnie ferroviaire, la surface de la roue est composée de deux cône tronqué d’ouvertures légèrement différentes. Il y a en plus un rebord, qui empêche la roue de quitter les rails. Le profil de ce bord è composé de différents arcs de cercles. Aussi le profil du rail, qui dans le modèle consistait en un arc de cercle, est en fait formé par l’union de cinq différents arcs de cercles.
Le virage par une paire de roues du train est donc sensiblement différente du virage par les roues d’une voiture, mais en réalité, dans les deux cas c’est cette science merveilleuse – la géométrie – qui joue un rôle basilaire.
Info supplémentaire
- Une paire de roues du train supportent environ une tonne. S’il s’agit de roues motrices, alors fixé à l’axe il y a en plus le pignon, ce qui fait atteindre la pois d’une tonne et demie. Le diamètre de la roue est d’environ un mètre.
- En Russie, pour des raisons stratégiques la distance entre les rails du train et les rails du métro sont les mêmes. L’écartement des rails, c’est à dire la distance entre les bords intérieurs des rails, est de 152 centimètres.
- Une courbe est considéré comme brusque, si son rayon est moins de 350 mètres. Dans ces courbes l’écartement peut être un peu plus large que la norme, mais au maximum de 3 cm.
- La longueur totale des chemins de fer en Russie est d’environ 87 mille kilomètres. La longueur des lignes de métro à Moscou (en 2011) est d’environ 300 km.
- Certains points de chaque roue se déplacent dans la direction opposée à celle du train. Pouvez–vous dire lesquels?