Peut-on plier le patron d’un polyèdre en corps fermé, dont les côtés proviendront non pas des morceaux des faces, mais des morceaux des surfaces planes?
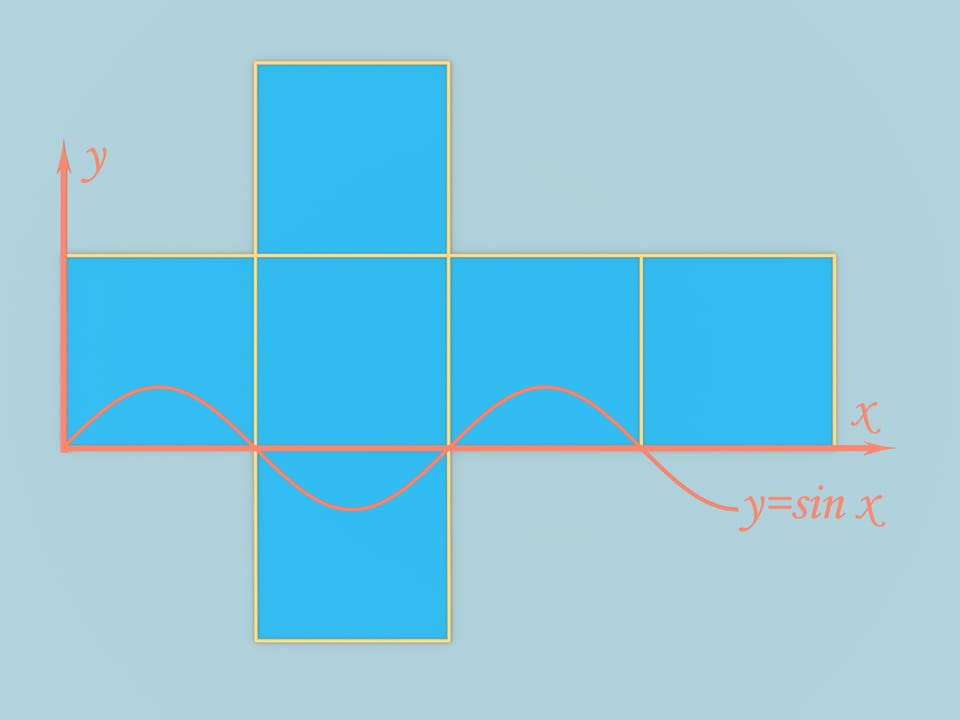
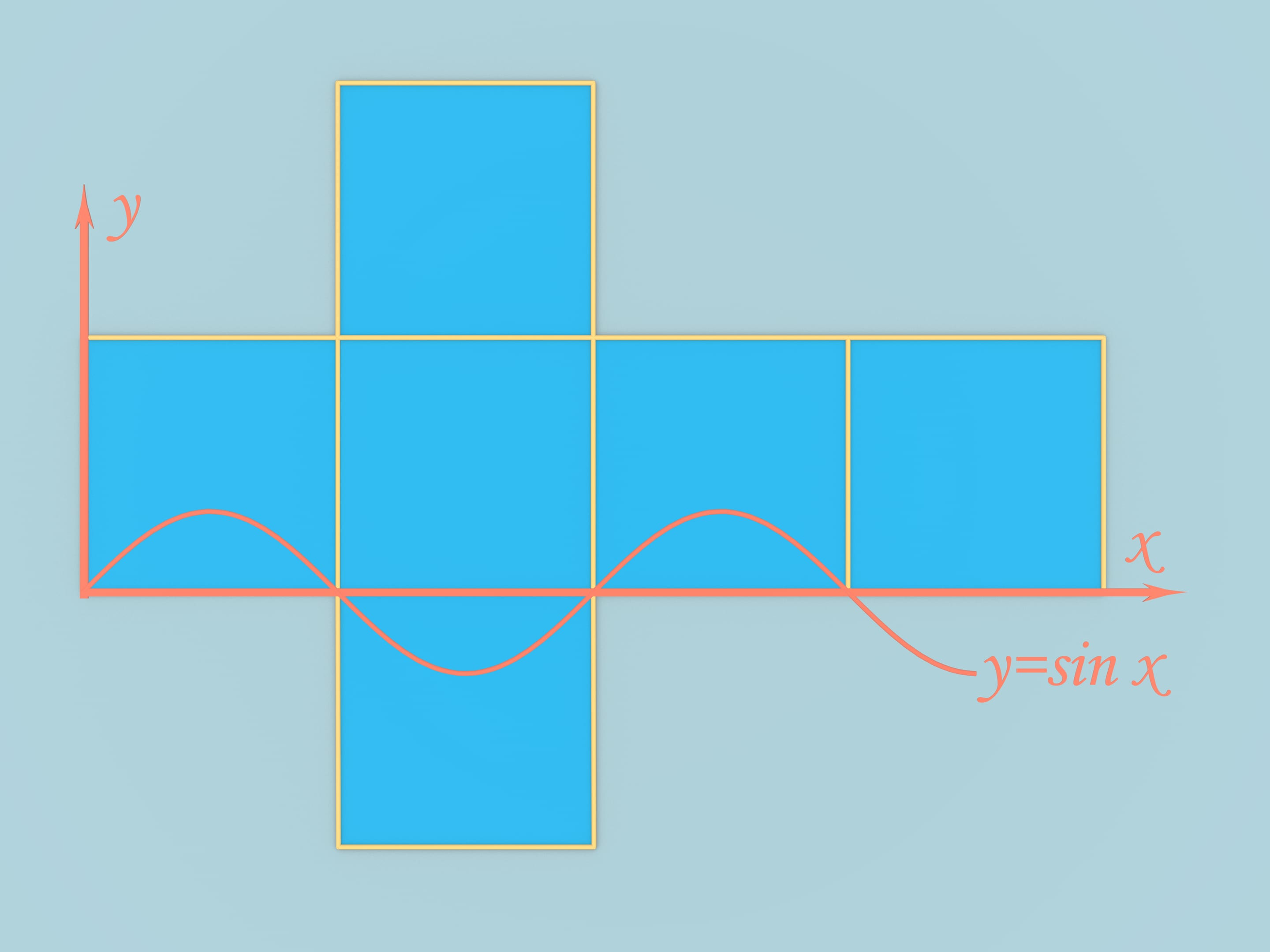
Prenons un cube dont la longueur du côté est $\pi$. Déplions-le en développement classique en croix et, spécialement en menant les axes des coordonnées, traçons la fonction $y=sin(x)$. Mettons les morceaux de développement, coupés en sinusoïde, et symétriques entre eux. Le développement n’a pas changé, tout comme les conditions de collage des côtés, selon le placement, ont été conservées. On peut plier un tel corps à partir de la figure obtenue.
Cependant, l’exemple étudié, bien que répondant à la question posée, comporte un inconvénient. Sa limite comporte deux morceaux, hérités d’un cube, qui ressemblent à des morceaux de plans. Après l’élaboration de cet exemple, la construction, ne présentant pas de “moins”, a surgi très vite.
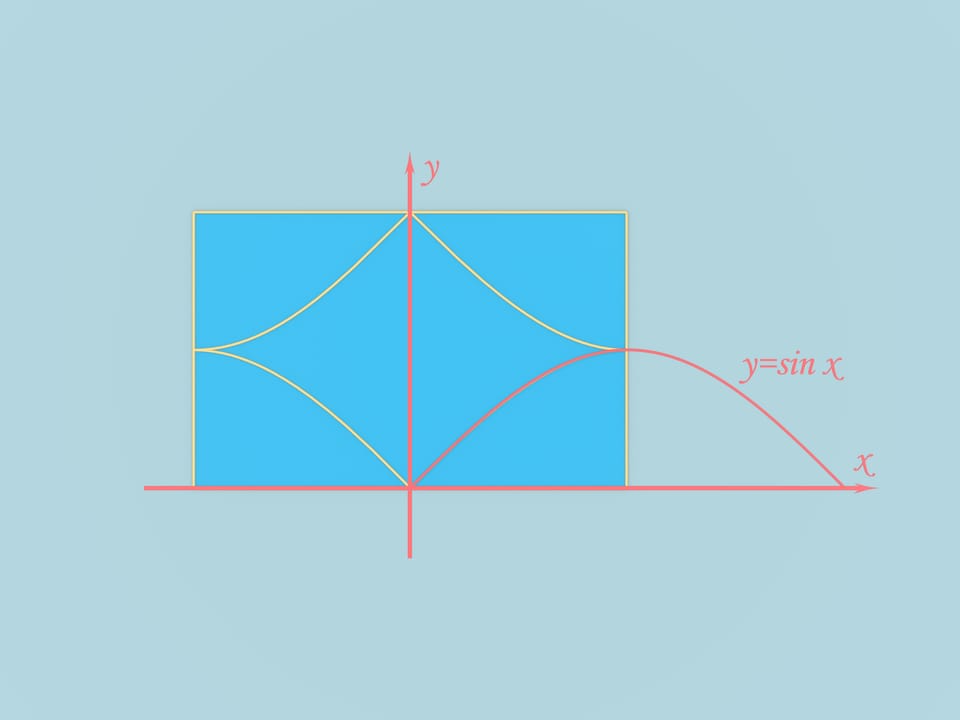
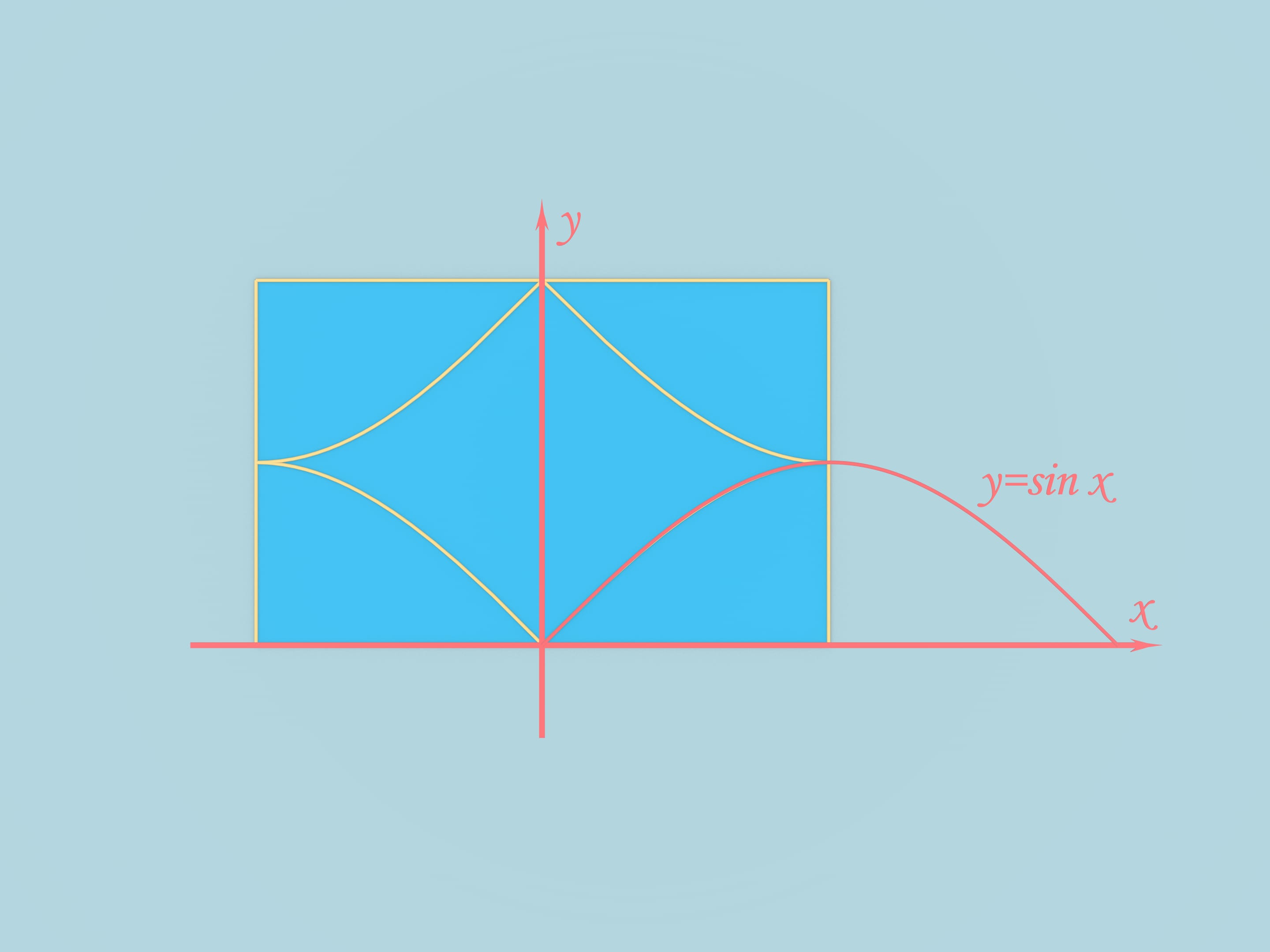
Prenons une feuille de papier rectangulaire de côté $\pi/2$. On peut plier, à partir d’une feuille de papier rectangulaire, une pyramide triangulaire. Pour cela, on fait correspondre les côtés aux centres des côtés voisins, et nous menons l’ arête correspondant au milieu des longueurs des côtés. En faisant , selon cette arête, on obtient une pyramide triangulaire.
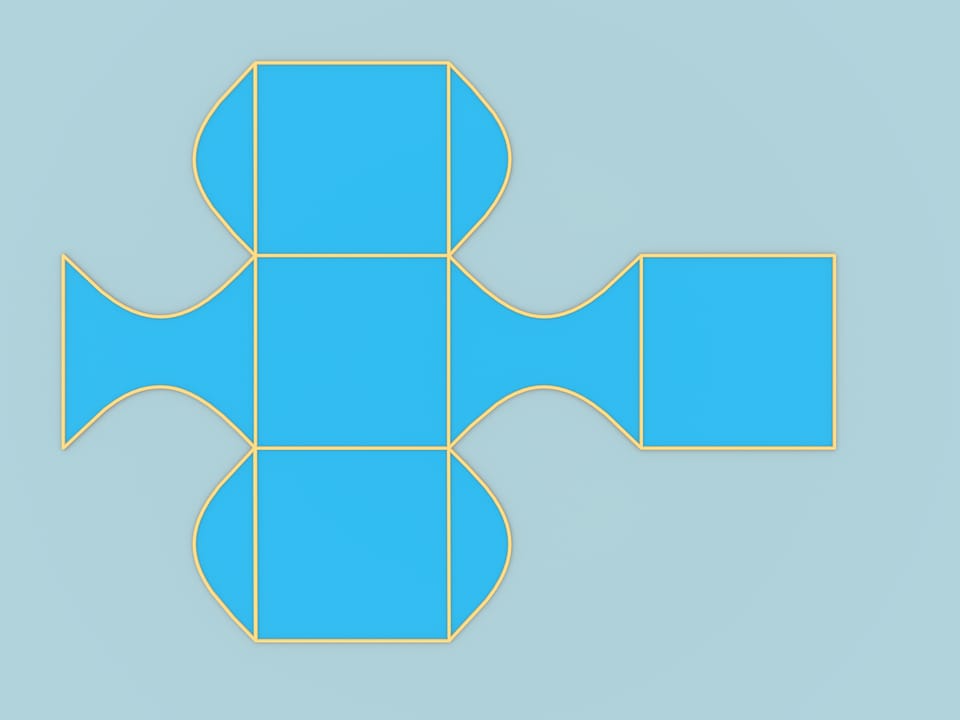
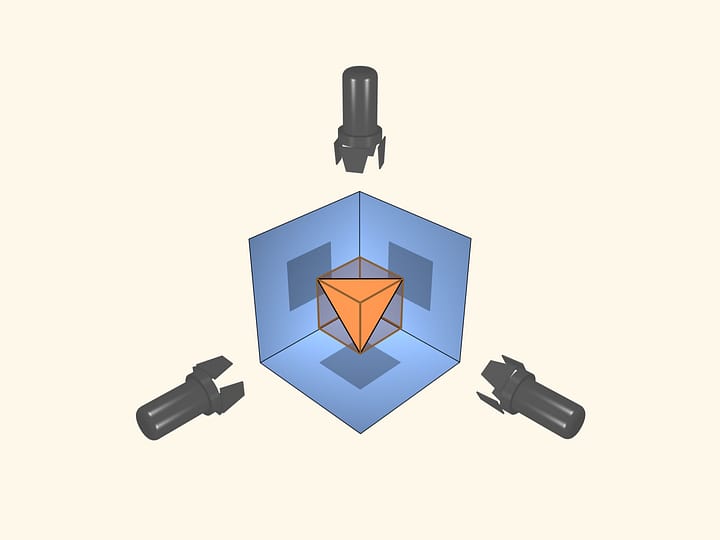
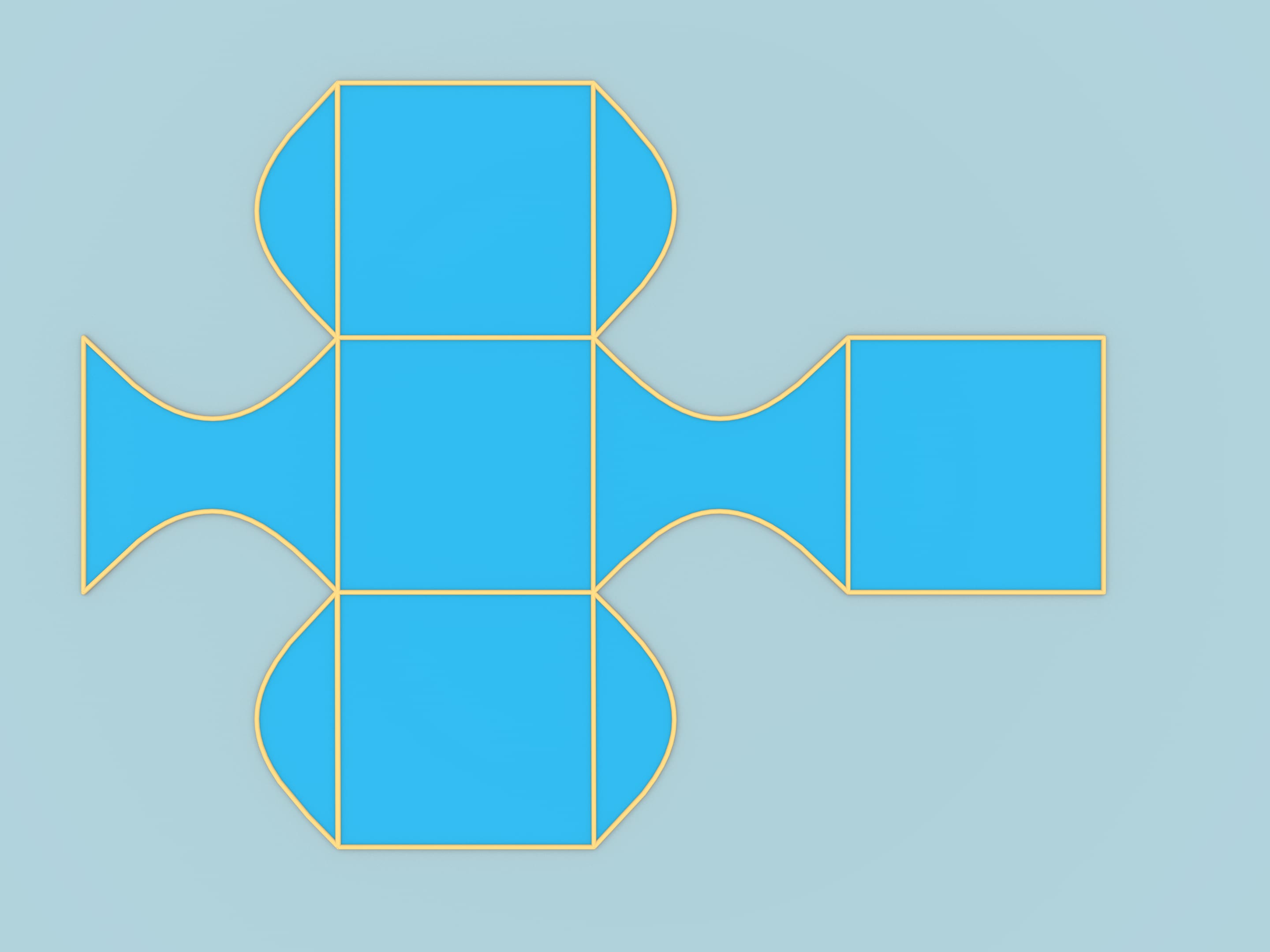
A partir de cette même feuille de papier, on peut obtenir une autre figure dont le bord de composera de surfaces planes. oignons les milieux des côtés voisins à ¼ de sinusoïde. Rassemblons la feuille selon ses arêtes. On obtient ce beau corps. Il obtient l’intersection de 3 cylindres: deux se touchent et un, disposé perpendiculairement à la disposition. Ainsi, le bord de la figure se compose de 3 morceaux de cylindres.
Il semblerait que de tels exemples durent être construits, si ce n’est à l’époque d’Archimède, il y a tout de même très longtemps. Cependant, les exemples étudiés ont été construits seulement en automne 2004